Kdo by neznal ten krásný pocit! Odpočívat na prohřáté písečné pláži a jen tak bezstarostně pozorovat vlny valící se k pobřeží. Kochat se nádhernými barvami, které oceán dokáže ze slunečních paprsků vykouzlit, a při tom se nechat ukolébat příjemným šuměním zpěněné vody.

Zdroj
Vlnění neodmyslitelně patří k prázdninové pohodě u moře. Kromě vln na vodní hladině jste pravděpodobně poznali ještě další příklady vlnění – zvuk a světlo. Vlnění je totiž jedním z nejběžnějších fyzikálních dějů. V této kapitole se dozvíte, co je podstatou vlnění, a podrobněji se zaměříme na vlnění mechanické.
Co je to vlnění?
Obecně můžeme říci, že zdrojem vlnění je vždy kmitající objekt. Zdroj rozkmitává okolní prostředí, kterým se kmitání šíří, a přenáší tím energii.
Vlnění je fyzikální děj, při němž se kmitání šíří prostředím.
Dochází při tom k přenosu energie bez přesunu látky.
Vlnění má nezastupitelný význam při komunikaci – můžeme jím přenášet informace bez nutnosti přesouvat látku.
Podle povahy „toho, co kmitá“, rozlišujeme
- vlny mechanické,
- vlny elektromagnetické,
- vlny gravitační.
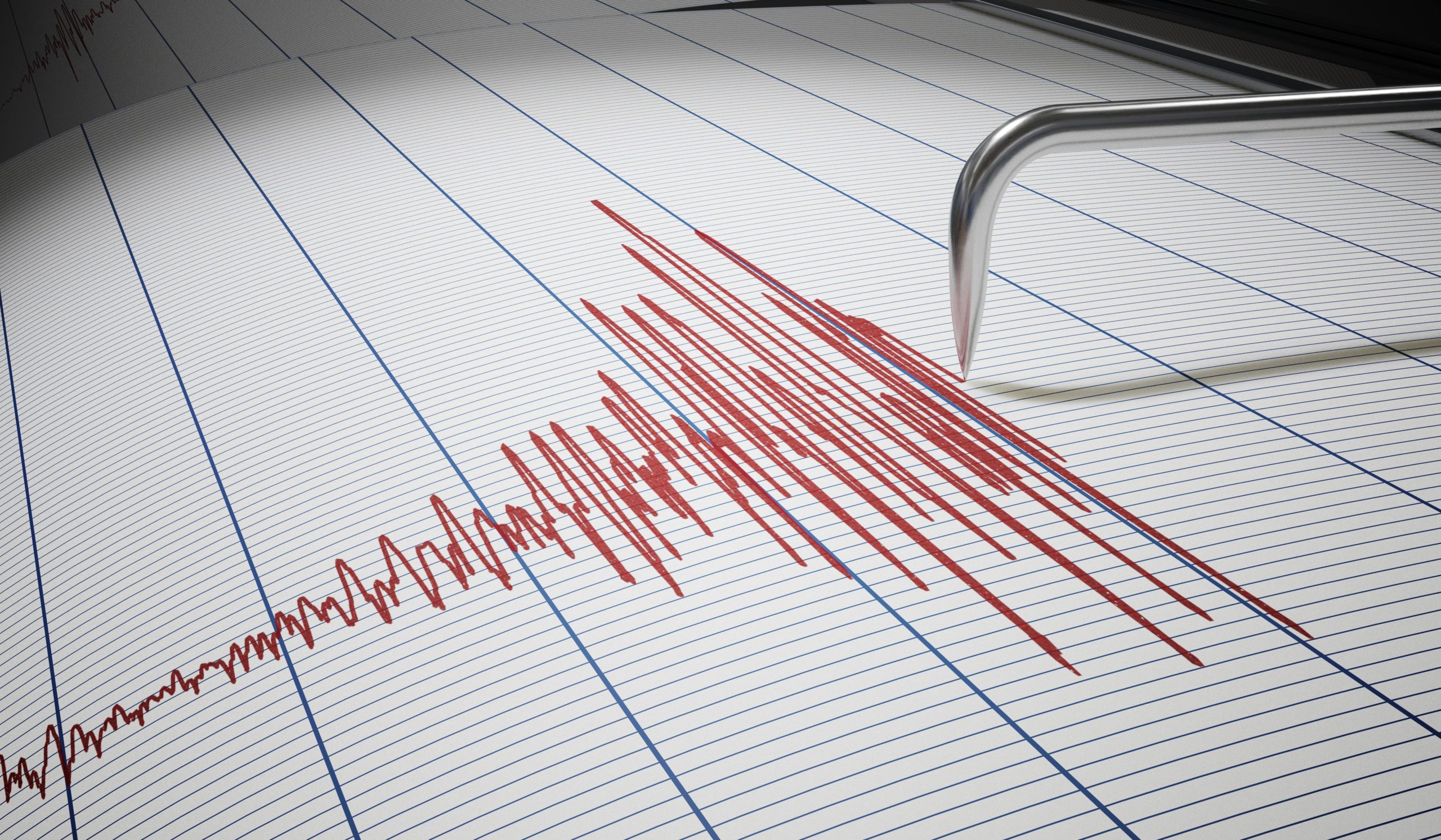
Mechanické vlnění je charakteristické tím, že kmitají atomy nebo molekuly v látce. Mechanické vlnění může existovat v pevných látkách, v kapalinách i v plynu, ale nemůže nastat ve vakuu. Rychlost šíření mechanických vln závisí na druhu vlny a typu prostředí. Zdrojem mechanických vln je vždy chvějící se těleso. Nejběžnějším příkladem mechanického vlnění jsou vlny na vodní hladině, zvuk a seismické vlny – viz níže.
Zdroj
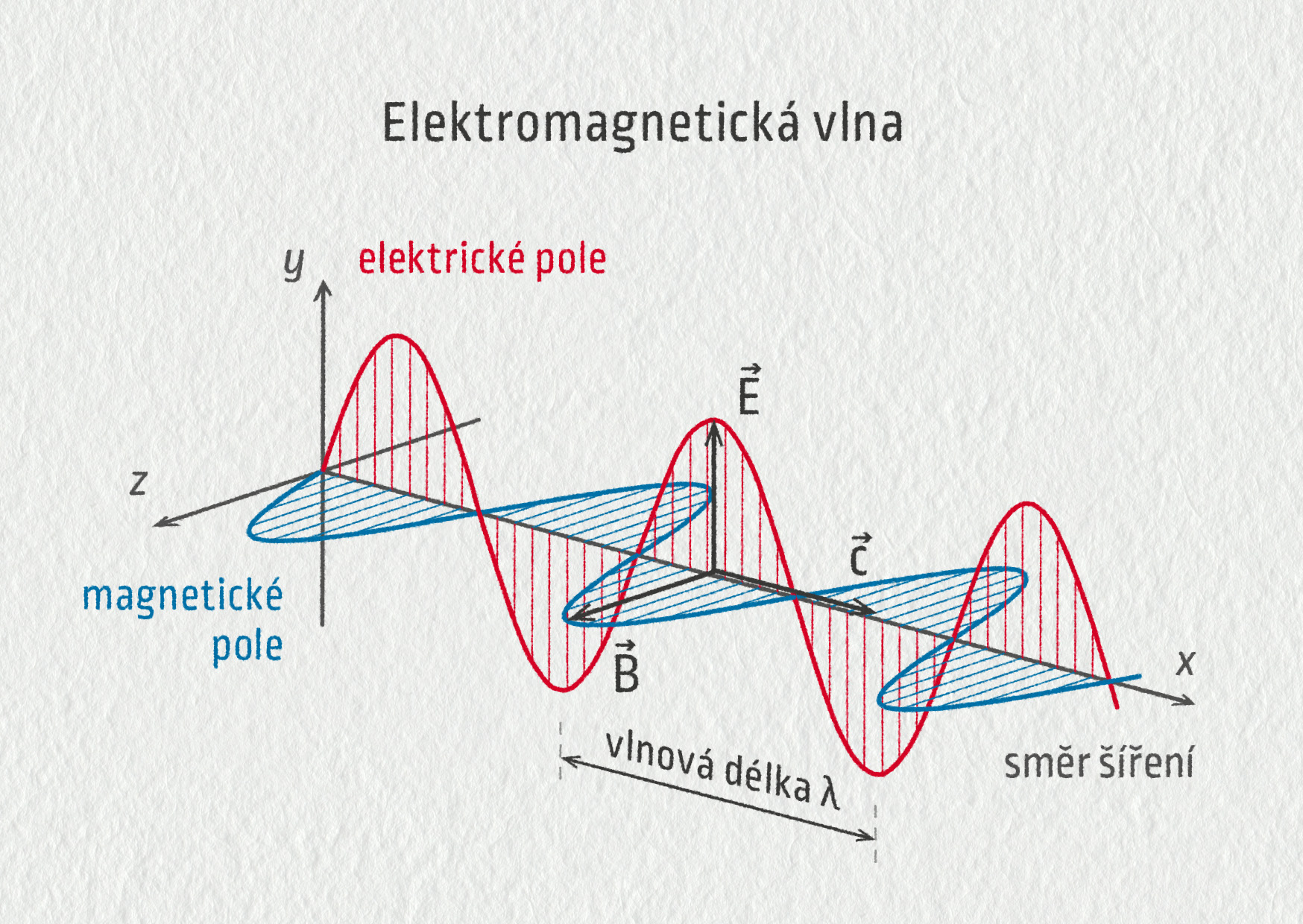
Elektromagnetické vlnění je tvořeno oscilacemi elektrického a magnetického pole. Toto vlnění není vázáno na přítomnost atomů a molekul, může se šířit v látkovém prostředí i ve vakuu. Rychlost šíření elektromagnetických vln je ve vakuu pro všechny pozorovatele stejná a je rovna 3 ⋅ 108 m/s. Zdrojem elektromagnetických vln jsou kmitající náboje, procesy v atomech a procesy doprovázející interakci elementárních částic. Všechny elektromagnetické vlny mají strukturu znázorněnou na obrázku 22.11, vzájemně se liší frekvencí. Z elektromagnetického spektra vnímá člověk pouze viditelné světlo, ovšem změřit a vytvořit dokážeme vlny rádiové, záření mikrovlnné, infračervené, ultrafialové, rentgenové a gama záření. Světlo a další elektromagnetické vlny mají pro lidstvo obrovský význam a jsou jim věnovány kapitoly 24 a 26.
Zdroj
Gravitační vlny spočívají v pravidelně se opakujících změnách zakřivení časoprostoru. Jejich existence byla předpovězena teoreticky již v roce 1916 Albertem Einsteinem. Poprvé byly tyto vlny experimentálně zaregistrovány až v roce 2015 na detektoru LIGO v USA. Rychlost šíření gravitačních vln je stejná jako rychlost vln elektromagnetických ve vakuu, tedy 3 ⋅ 108 m/s. Více podrobností najdete na konci kapitoly 17.

Zdroj
Vlnění podélné a příčné
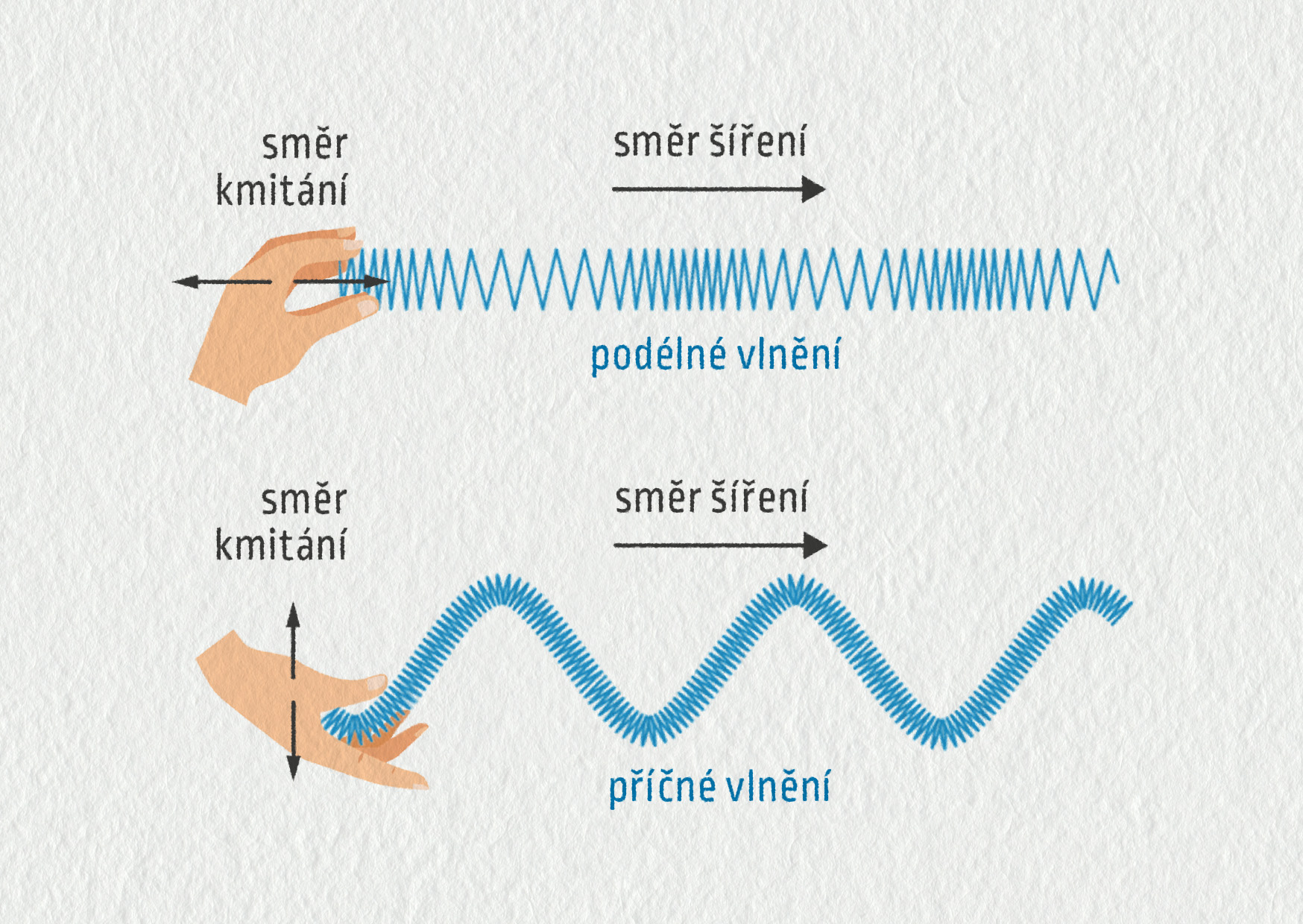
Podle směru kmitání rozlišujeme vlny podélné a vlny příčné.
U podélného vlnění je směr kmitání rovnoběžný se směrem šíření vlny. Jedná se typicky o tlakové vlny – například zvuk v kapalinách a plynech, ale i některé druhy seismických vln. Animace.
U příčného vlnění je směr kmitání kolmý na směr šíření vlny. Jde typicky o elektromagnetické vlny ve vakuu nebo některé druhy mechanických vln v pevných látkách. Animace.
Zdroj
Příklady mechanického vlnění
V dalším textu této kapitoly se budeme zabývat pouze mechanickými vlnami.
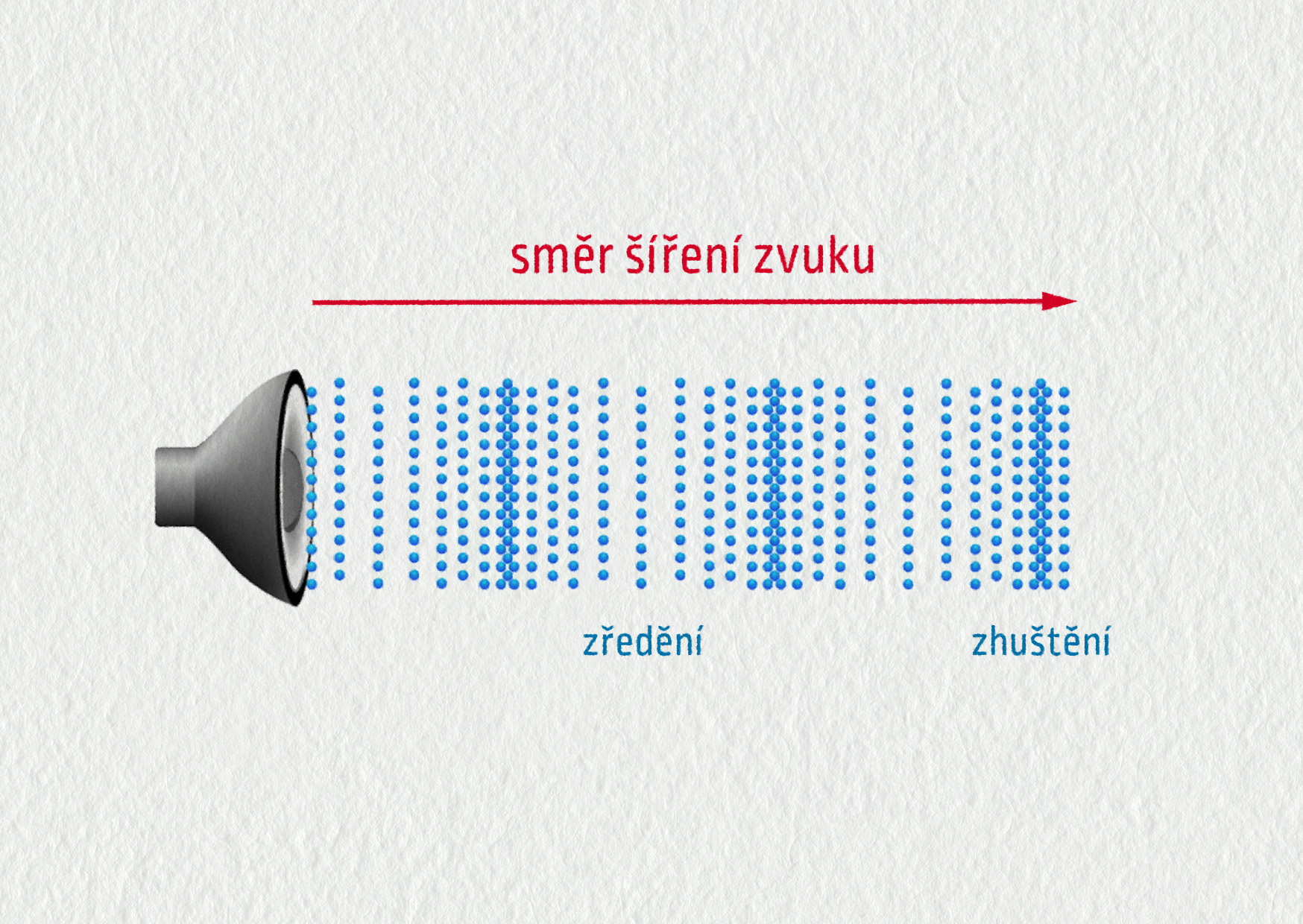
Zvuk je mechanické vlnění, které vnímáme sluchem. Zdrojem zvukového vlnění je vždy kmitající těleso, například membrána reproduktoru, kmitající hlasivky, kmitající struna. Vibrující membrána reproduktoru se pohybuje tam a zpět a způsobuje zhušťování a zřeďování molekul okolního vzduchu ve své těsné blízkosti – viz obrázek 22.15. Zhuštění vzduchu, čili tlaková vlna, se postupně šíří od zdroje do prostoru. Molekuly vzduchu kmitají tam a zpět a svým kmitáním předávají energii od zdroje do prostoru. Tento kmitavý pohyb molekul se skládá s jejich chaotickým tepelným pohybem.
Zdroj
Zvuk v plynech a kapalinách je vždy podélné vlnění, v pevných látkách může mít podobu jak podélného, tak příčného vlnění.

Zdroj
Vlny na vodní hladině vzniknou nejčastěji dopadem předmětu na hladinu nebo působením větru. Přestože v určitém místě můžeme pozorovat kmitání výšky hladiny nahoru a dolů, nejedná se o příčné vlnění. Ve skutečnosti opisují molekuly vody (a s nimi i drobné pevné částice a plankton) v hluboké vodě téměř kruhové trajektorie. Míč ležící na hladině by se pohupoval jak ve svislém, tak vodorovném směru.
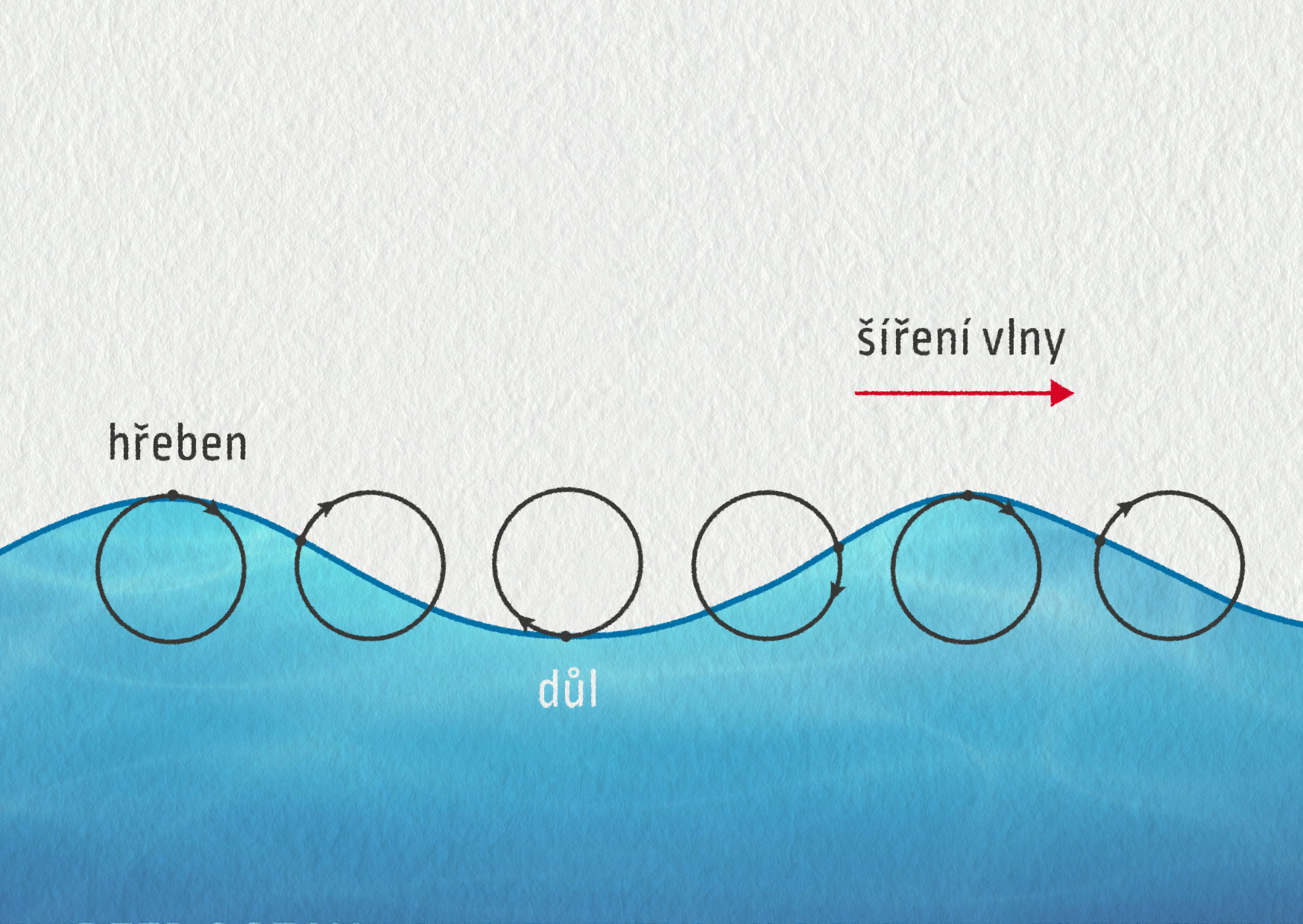
Zdroj
Zemětřesení neboli seismické vlny jsou mechanické vlny šířící se Zemí. Obvykle se dělí na vlny objemové (P a S) a povrchové (R a L). Vlna P je podélná a jako jediná se může šířit tekutým pláštěm a tekutými oblastmi vnějšího jádra Země. Vlna S je příčná a prochází pevnou zemskou kůrou. Vlny R (Rayleighova, která připomíná vlny na vodní hladině) a L (Loveho, příčná) se mohou šířit jen při povrchu zemské kůry. Každý druh vlny má jinou rychlost šíření, proto se z několika málo měřících stanovišť dá přesně zrekonstruovat poloha, čas vzniku a síla zemětřesení – viz motivační aktivita v této kapitole.
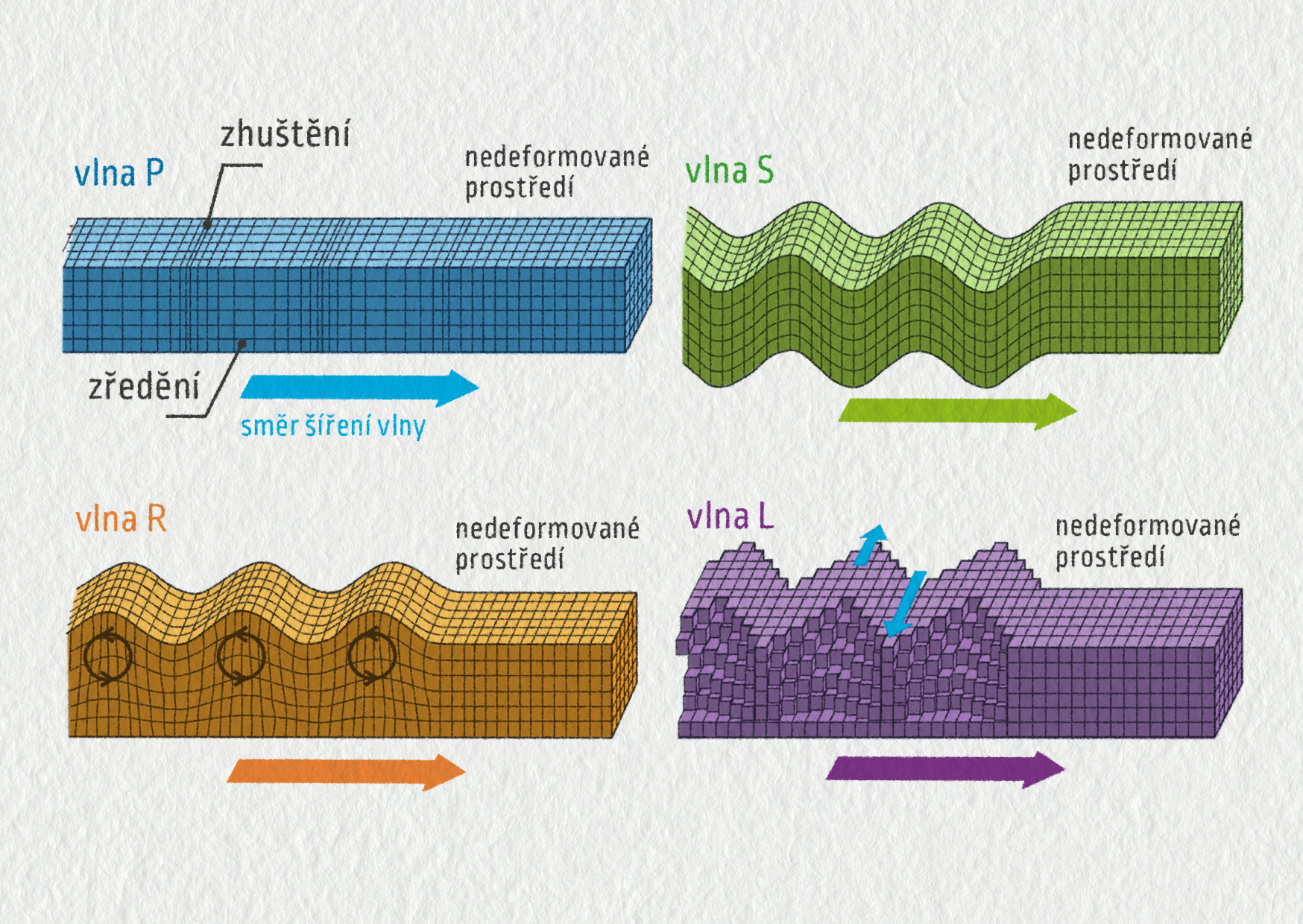
Zdroj
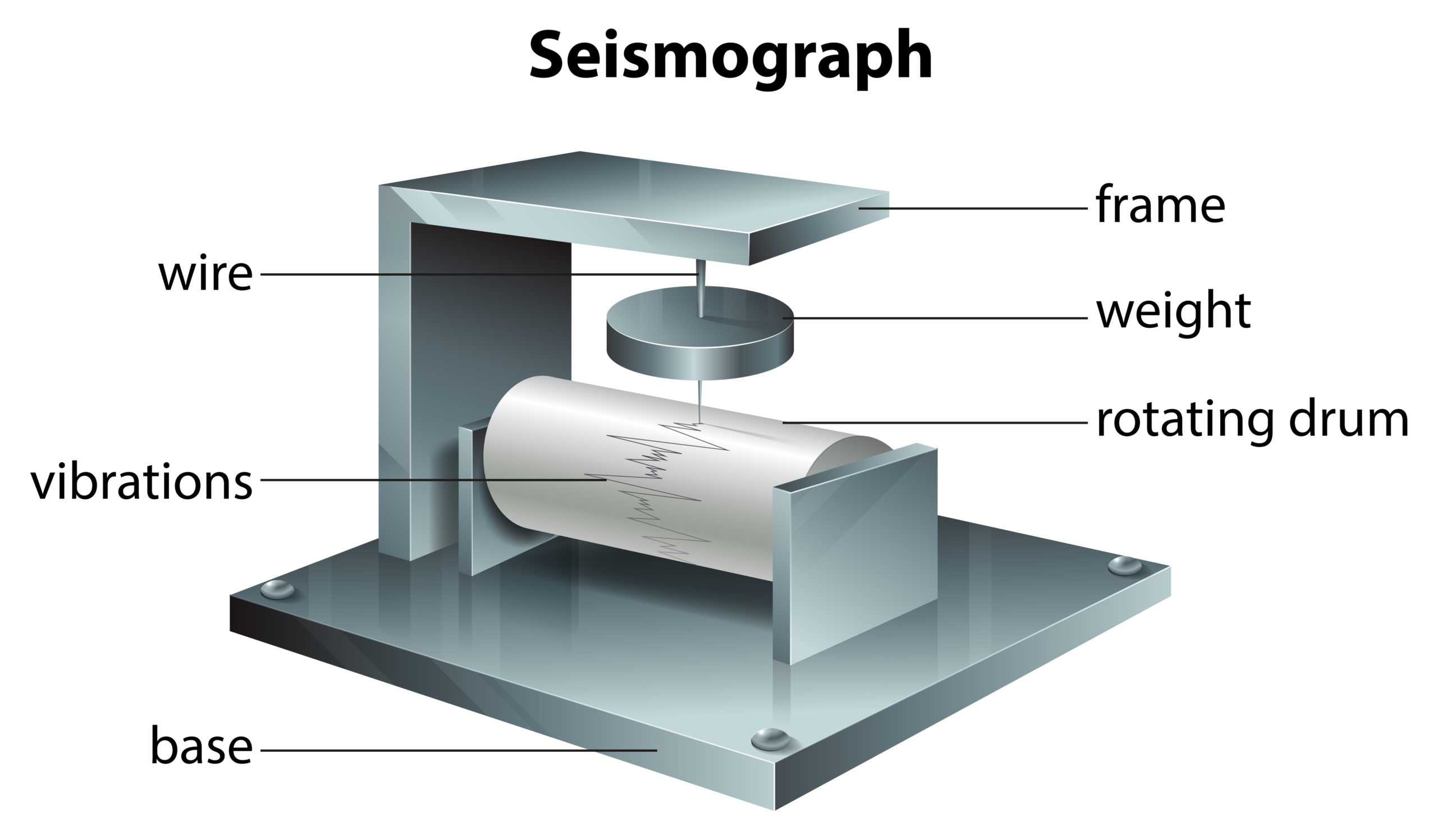
Zdroj
Fyzikální veličiny popisující vlnění
Každá mechanická vlna je charakterizována rychlostí šíření prostředím a amplitudou. V případě periodických vln, čili vln vznikajících pravidelným chvěním zdroje, se k nim přidává ještě frekvence, perioda a vlnová délka. Připomeňme se jejich definice.
Velikost rychlosti šíření vlnění vypočítáme ze známého vztahu \(v=s/t\), tedy jako dráhu, kterou vlna urazí za časovou jednotku. Vlnění se může šířit všemi směry, které má k dispozici. Trhneme-li prudce zahradní hadicí, vzniklá vlna se šíří podél hadice, tedy v 1D. Po vhození kamene do vody se na hladině vytvoří soustředné kruhové vlny, šíří se tedy ve 2D. Zvukové vlny vzniklé mluvením se šíří do všech směrů, tedy ve 3D. Z mechaniky víme, že rychlost je vektorová veličina, v následujícím výkladu budeme uvažovat pouze velikost rychlosti šíření ve směru, který nás zajímá.
Rychlost šíření závisí na druhu vlny a na prostředí, v němž se šíří. Situace je dobře patrná pro zvuk, u kterého v různých prostředích naměříme řádově tyto hodnoty:
- v kovech 5 000 m/s,
- v kapalině 1 500 m/s,
- ve vzduchu 340 m/s.
V pevné látce jsou atomy blízko u sebe a vzájemně jsou propojeny pevnými vazbami, takže vychýlení určité vrstvy atomů se ihned projeví silou působící na sousední vrstvu atomů. Naopak v plynu jsou atomy a molekuly výrazně dál od sebe a působí na sebe pouze během vzájemných srážek. Proto je přenos energie mezi částicemi výrazně pomalejší.
Velikost rychlosti šíření zvuku ve vzduchu závisí mírně i na jeho teplotě. Pro suchý vzduch a teploty blízké pokojové teplotě můžeme používat přibližný vztah
\[ v_\mathrm{z} = 331{,}57 + 0{,}607t\;, \]kde \(t\) je teplota vzduchu ve °C a \(v_\mathrm{z}\) rychlost zvuku v m/s.
Jak uvidíme v oddílu věnovaném hudebním nástrojům, teplota, a tedy i rychlost šíření ovlivňují výšku tónu vznikajícího v dechových nástrojích, tedy jejich ladění.
Při jaké teplotě má rychlost zvuku ve vzduchu hodnotu 340 m/s? Napište číselný výsledek zaokrouhlený na celé °C.
Na základě termodynamických úvah se dá dokázat, že rychlost šíření zvuku v ideálním plynu je
\[ v_\mathrm{z} = \sqrt{\frac{\gamma RT}M}\;, \]tedy přímo úměrná odmocnině z termodynamické teploty \(T\) (vyjádřené v kelvinech). Konstanta \(R\) je univerzální plynová konstanta \(R=8{,}314\ \mathrm{J/mol}\cdot\mathrm{K}\), \(\gamma\) je Poissonova konstanta pro daný plyn (pro dvouatomové molekuly \(\gamma=1{,}40\)) a \(M\) je molární hmotnost plynu.
Je tedy zřejmé, že rychlost zvuku ve vzduchu nezávisí na atmosférickém tlaku, ale naopak závisí na jeho vlhkosti prostřednictvím molární hmotnosti \(M\) a že tato závislost není přesně lineární.
Známe-li rychlost zvuku \(v_{\mathrm{z}0}\) při určité teplotě \(T_0\), můžeme rychlost zvuku při jiné teplotě \(T\) vypočítat ze vztahu \(v_\mathrm{z}=v_{\mathrm{z}0}\sqrt{T/T_0}\).
Lineární vztah uvedený ve výkladu lze z tohoto přesného odvodit Taylorovým rozvojem pro malé odchylky \(\Delta T\) od teploty \(T_0\). Vezmeme \(T_0=273{,}15\ \mathrm{K}\), \(v_{\mathrm{z}0}=331{,}57\ \mathrm{m/s}\) a teplotu \(T=T_0+\Delta T\). Potom pro \(\Delta T\ll T_0\) platí
\[ v_\mathrm{z} = \] \[ = v_{\mathrm{z}0}\sqrt{\frac{T}{T_0}} = \] \[ = v_{\mathrm{z}0}\sqrt{\frac{T_0+\Delta T}{T_0}} = \] \[ = v_{\mathrm{z}0}\sqrt{1+\frac{\Delta T}{T_0}} \approx v_{\mathrm{z}0}\left(1+\frac{\Delta T}{2T_0}\right) = \] \[ = 331{,}57 + 0{,}607\Delta T\;. \]Ve fyzice je amplituda vlnění definována jako maximální výchylka z rovnovážné polohy. V případě vln je to tedy maximální výchylka kmitajících částic prostředí vůči stavu, kdy se vlna nešíří. V drtivé většině případů dochází při kmitání k vnitřnímu tření v prostředí. To způsobuje, že je mechanická vlna tlumená – její amplituda klesá se vzdáleností od zdroje.
Amplituda vlnění klesá s rostoucí vzdáleností od zdroje i z jiného důvodu než jen kvůli tření. Tento pokles je dobře patrný u zvuku – vzdalujeme-li se od zdroje, hlasitost klesá.
Uvažujme vlny v prostoru (3D). Předpokládejme, že zdroj mechanického vlnění Z předává do části prostoru vymezené prostorovým úhlem \(\Omega\) stálé množství energie za sekundu. Předpokládejme dále, že vnitřní tření v prostředí je zanedbatelné. Částice prostředí si kmitáním postupně předávají vyzářenou energii. Vyzářená energie tedy musí nejdříve projít plochou \(S_1\), pak plochou \(S_2\) atd. (viz obrázek 22.20). Množství energie, které vlny přinesou na 1 m2 plochy za 1 s, nutně klesá se vzdáleností od zdroje, vlna tedy přirozeně „slábne“. Proto i v prostředí bez tření bude amplituda vlnění ve větší vzdálenosti \(r_2\) od zdroje vždy menší než v kratší vzdálenosti \(r_1\).
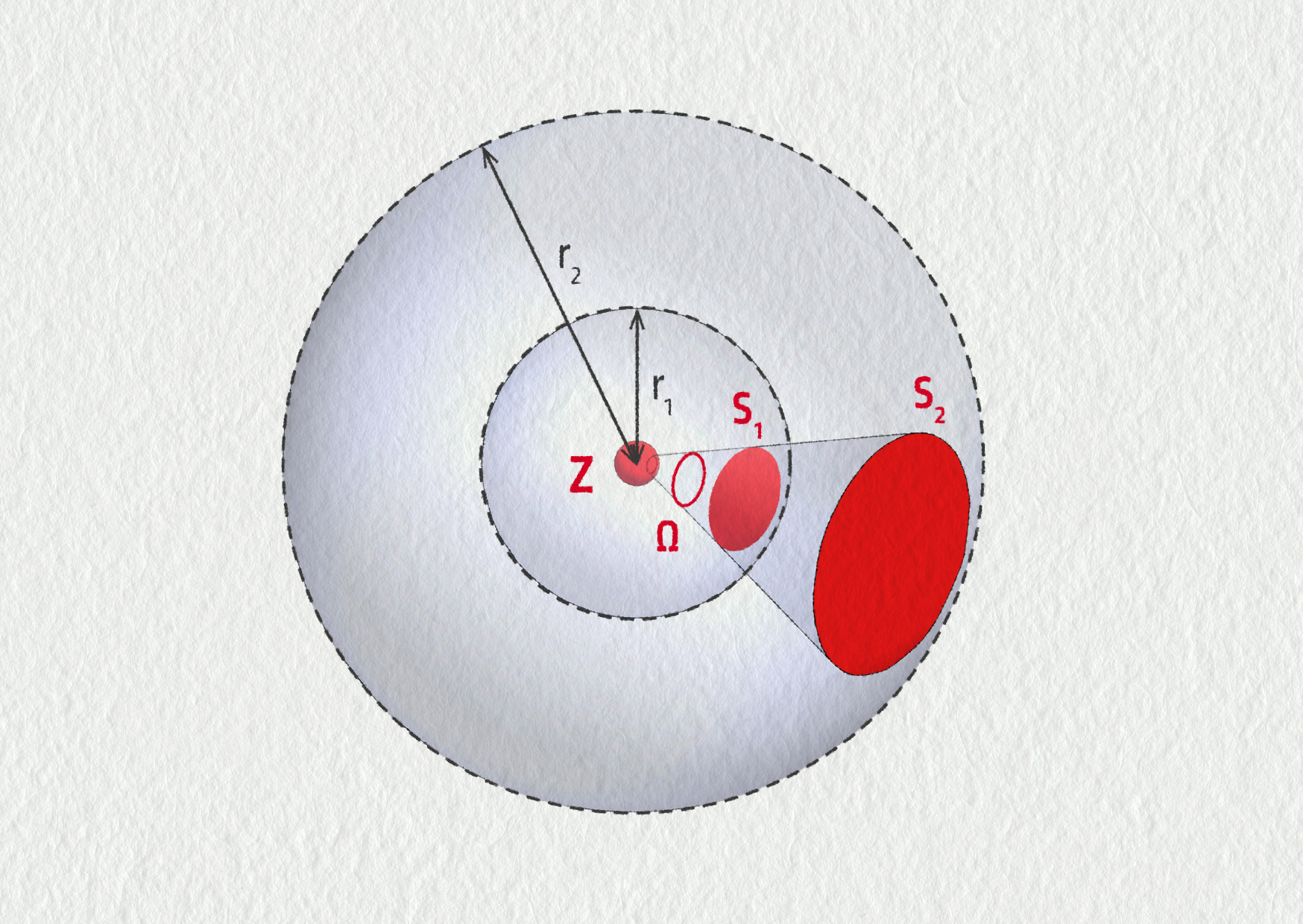
Zdroj
Energie nesená vlněním je úměrná druhé mocnině amplitudy. Potom ve 3D klesá energie kvadraticky a amplituda lineárně s rostoucí vzdáleností. Podrobněji věc rozebereme pro intenzitu zvuku.
Situace je jiná ve 2D (např. vlny na vodní hladině vytvořené dopadem předmětu) a v 1D (např. šíření zvuku uvnitř roury). Můžete si snadno odvodit, že ve 2D klesá energie lineárně a amplituda jako funkce odmocnina. Při šíření pouze v jednom rozměru a při zanedbatelném tření se vlnění teoreticky netlumí (viz provázkový telefon).
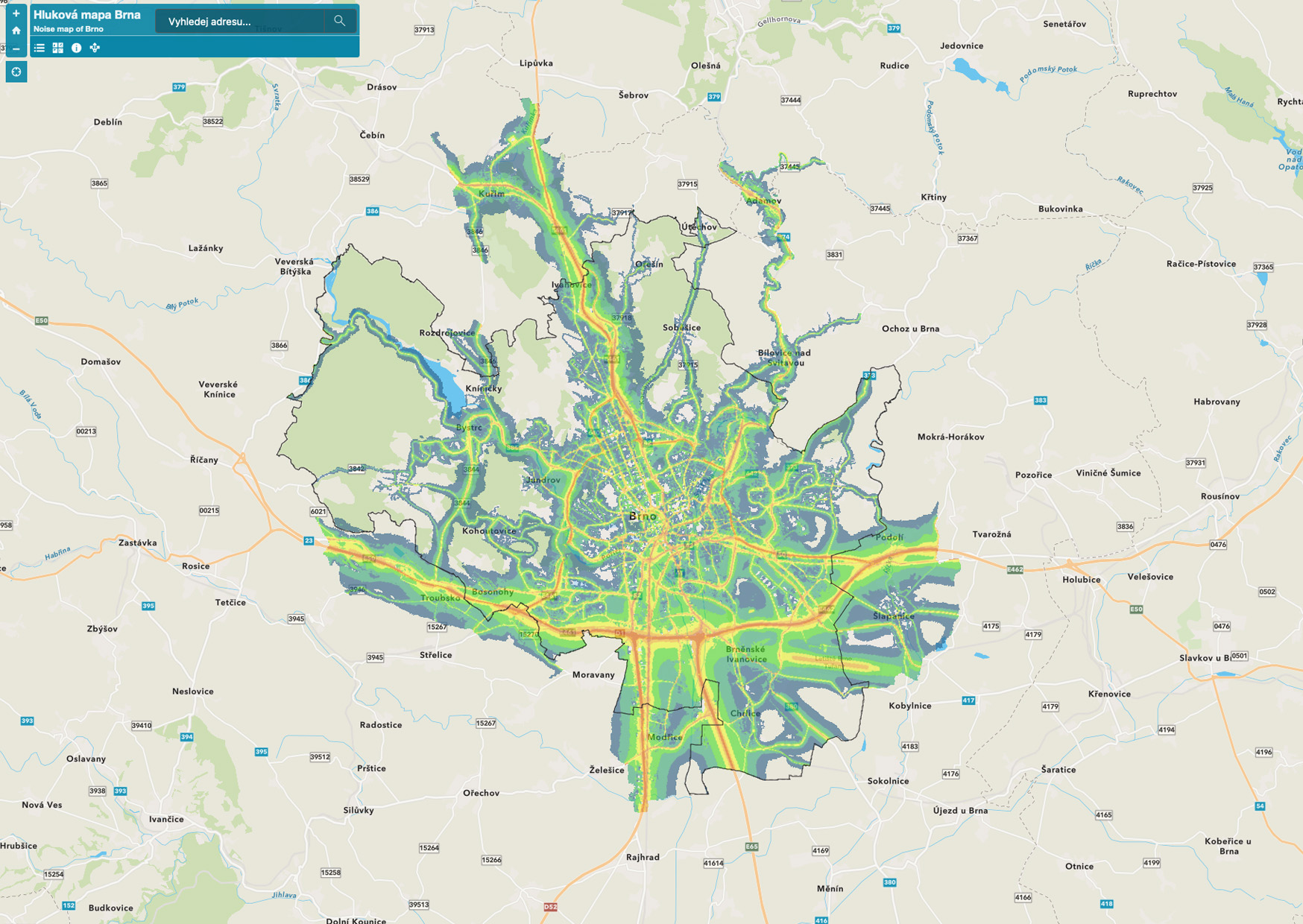
Fyzikálně zajímavá je i závislost amplitudy na vzdálenosti od zdroje, který není bodový – typickým příkladem je rovnoměrně hučící dálnice (lineární zdroj). Situace má válcovou symetrii, energie klesá lineárně se vzdáleností, a tedy amplituda klesá jako funkce odmocnina. Znamená to, že jestliže se vzdalujeme od dálnice, hluk klesá pomaleji než například hluk od bodového zdroje.
Zdroj
Perioda vlnění je rovna době, za niž částice prostředí, kterým se šíří vlna, vykoná jeden kmit. Perioda vlnění je dána periodou kmitání zdroje.
Frekvenci vlnění definujeme jako počet kmitů, které vykoná částice prostředí za sekundu. Obě tyto veličiny jsou podrobněji vysvětleny v kapitole 21.
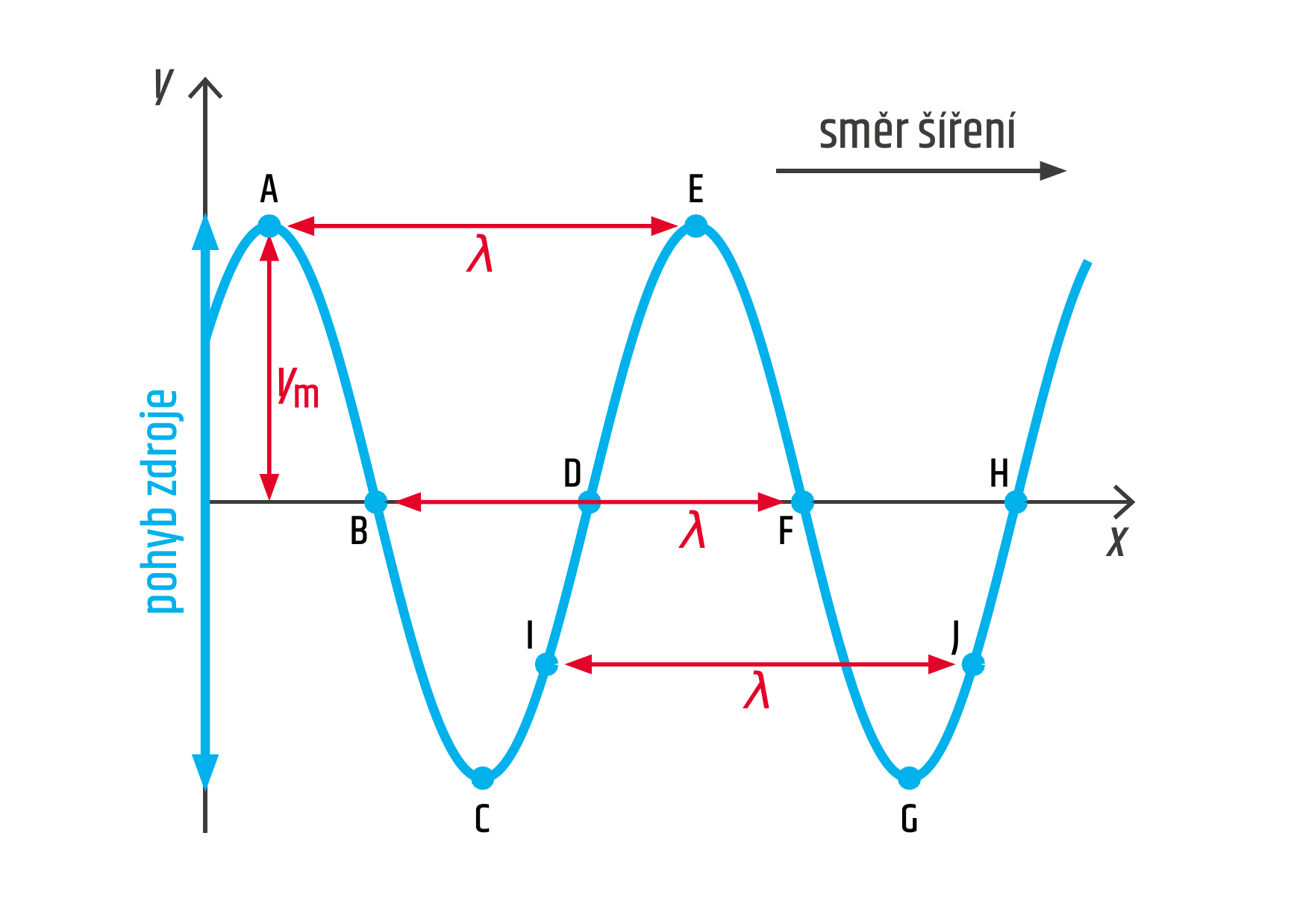
Veličinou charakteristickou pro periodické vlnění je vlnová délka. Značí se řeckým písmenem \(\lambda\) (lambda) a její jednotkou je metr. Vlnová délka je definována jako dráha, kterou vlna urazí za jednu periodu. Dráha uražená při pohybu stálou rychlostí je \(s=vt\), takže pro čas rovný jedné periodě \(t=T\) snadno odvodíme základní vztah pro vlnovou délku:
\[ \lambda = vT = \frac vf\;. \]Definice vlnové délky
Vlnová délka je rovna dráze, kterou vlna urazí za jednu periodu.
\[ \lambda = vT \]\(\lambda\) – vlnová délka
\(v\) – rychlost šíření vlnění
\(T\) – perioda vlnění
Vlnová délka má zajímavou vlastnost, díky které se snadno měří. Vlnová délka je totiž vzdálenost, po níž se vlna v prostoru opakuje, čili prostorová perioda vlny. Učeně řečeno, vlnová délka je nejmenší vzdálenost mezi dvěma částicemi, které kmitají se stejnou fází, měřená ve směru šíření vlny. Vlnová délka je tedy vzdálenost například mezi dvěma sousedními hřbety vln na vodní hladině.
Zdroj
Z počtu hřbetů vln za minutu můžeme určit frekvenci vlnění \(f=12/(60\ \mathrm{s})=0{,}2\ \mathrm{Hz}\). Časová perioda je tedy zřejmě 5 s. K výpočtu vlnové délky bychom potřebovali znát ještě rychlost šíření vln.
Pomocí obrázku 22.23 vysvětlete, jak vznikají a jak se šíří vlny tsunami a proč u pobřeží roste jejich výška. Rychlost šíření povrchových vln na vodě závisí na hloubce, přesněji řečeno, se zmenšující se hloubkou klesá i rychlost šíření vln.

Zdroj
Vlna tsunami vzniká nejčastěji vibracemi mořského dna při pohybu litosférických desek během zemětřesení nebo výbuchem podmořské sopky. Na volném hlubokém moři mají vzniklé vlny na hladině vlnovou délku řádově stovky kilometrů a amplitudu desítky centimetrů, takže pro plavidla nepředstavují reálné nebezpečí. Se zmenšující se hloubkou klesá i rychlost šíření vln. Podle vztahu \(\lambda=v/f\) vidíme, že jak se vlna šíří k pobřeží, její vlnová délka se musí zmenšovat. Jenže voda je téměř nestlačitelná, takže objem vody původně rozprostřený do šířky stovky kilometrů se postupně zvedá do výšky a vytváří u pobřeží ničivou vlnu, která následně smete vše, co jí stojí v cestě.
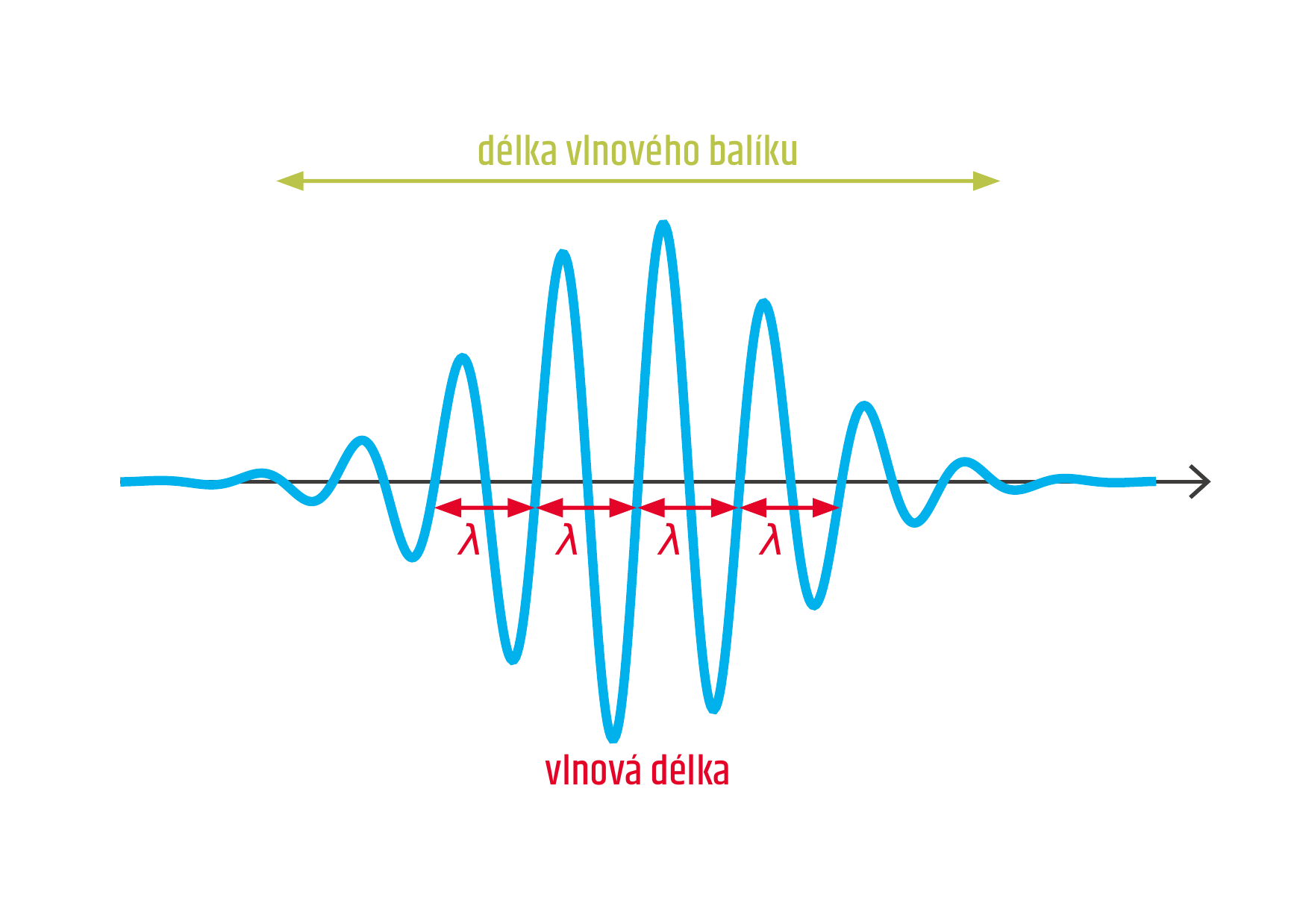
Žádný zdroj mechanického vlnění nekmitá nekonečně dlouho. Proto je každá mechanická vlna v čase i v prostoru omezená – má začátek a konec. Takto omezenému vlnovému útvaru se říká vlnový balík neboli vlnové klubko. Vlnový balík se matematicky dá získat složením velkého počtu vln různých frekvencí (různých vlnových délek). Pozoruhodné je, že tento balík se jako celek pohybuje v některých hmotných prostředí jinou rychlostí (tzv. grupová rychlost), než je rychlost šíření vln v tomto prostředí (tzv. fázová rychlost). Grupová rychlost udává rychlost, jakou vlny přenášejí energii prostředím. Například pro vlny na hluboké vodě je fázová rychlost dvojnásobkem grupové rychlosti.
Zdroj
Rovnice postupné vlny
Podobně jako jsme v kapitole 21 zkoumali kmitání jediného tělesa, chtěli bychom nyní odvodit rovnici popisující šíření vlny. Vyjdeme z následujících zjednodušujících předpokladů:
- zdroj vlnění se nachází v počátku soustavy souřadnic a kmitá harmonicky podle předpisu \(y_\mathrm{Z}=y_\mathrm{m}\sin(\omega t)\),
- vlna se šíří jen v kladném směru osy \(x\) a není tlumena.
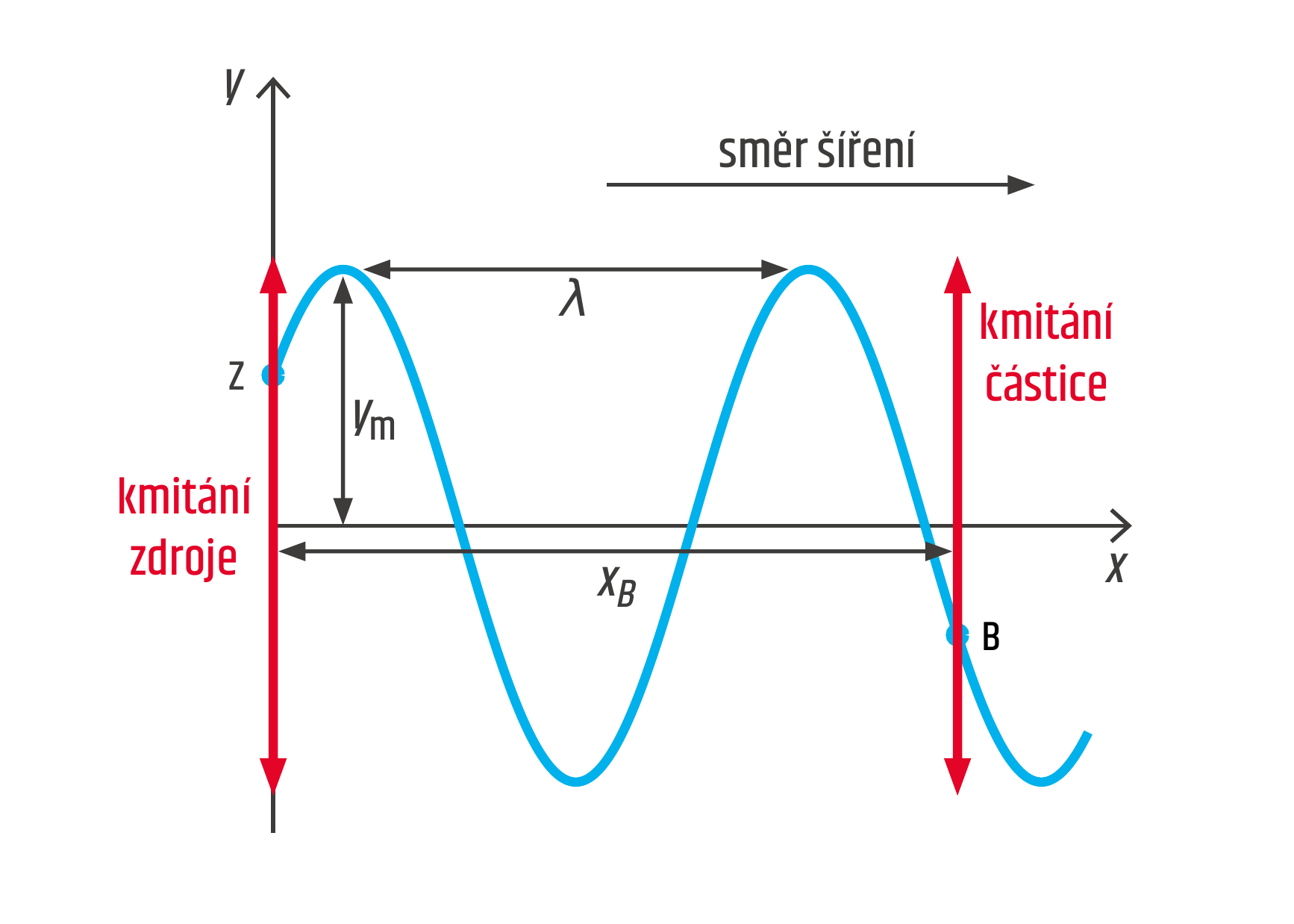
Základem naší úvahy je fakt, že každá částice prostředí vykonává podobný pohyb jako zdroj, ovšem kmitání této částice se děje se zpožděním. Toto zpoždění – označíme je \(\Delta t\) – se rovná době, za kterou vlna dospěje od zdroje Z do místa, kde se uvažovaná částice nachází (na obrázku 22.25 je to bod B).
Zdroj
Zpoždění \(\Delta t\), s jakým kmitá bod B oproti zdroji Z, snadno určíme z definice rychlosti šíření vlny \(\Delta t=x_B/v\).
Jelikož částice v bodě B opakuje opožděně pohyb zdroje, potom pro výchylku z rovnovážné polohy uvažované částice platí
\[ y_B = y_\mathrm{Z}(t-\Delta t) = y_\mathrm{m}\sin\bigl(\omega(t-\Delta t)\bigr)\;. \]Dosazením za úhlovou frekvenci \( \omega =2\pi/T \) a úpravou s využitím \(\lambda=vT\) odvodíme rovnici pro kmitání částice v bodě B
\[ y_B = y_\mathrm{m}\sin\left[2\pi\left(\frac tT-\frac{x_B}{\lambda}\right)\right]\;. \]Okamžitá výchylka z rovnovážné polohy částice v bodě B závisí na dvou proměnných – na čase t a na vzdálenosti od zdroje \(x_B\).
Zobecněním pro libovolný bod prostředí ve vzdálenosti \(x\) od zdroje získáváme rovnici postupné vlny šířící se ve směru osy \(x\)
\[ y(x) = y_\mathrm{m}\sin\left[2\pi\left(\frac tT-\frac x{\lambda}\right)\right]\;. \]Tato rovnice určuje, jak bude kmitat libovolný bod prostředí, kterým se šíří vlna. Tím je ovšem vlna jednoznačně popsána. Můžete si všimnout, že harmonická vlna je periodická v čase (perioda \(T\)) i v prostoru (vlnová délka \(\lambda\)), přičemž tyto dva parametry jsou vzájemně svázány rychlostí šíření \(\lambda=vT\).
Výraz v hranaté závorce
\[ \varphi = 2\pi\left(\frac tT-\frac x{\lambda}\right) \]se nazývá fáze vlny, a jelikož je argumentem funkce sinus, vyjadřuje se v radiánech.
Vliv jednotlivých parametrů si můžete vyzkoušet v animaci.
Mechanická vlna je popsána rovnicí \(y=0{,}15\sin(0{,}90t-0{,}31x)\). Číselné hodnoty jsou vyjádřeny v základních jednotkách SI.
- Určete amplitudu, periodu, vlnovou délku, frekvenci a rychlost šíření vlny.
- Načrtněte tvar vlny v čase \(t=2\ \mathrm{s}\).
- Znázorněte časový průběh kmitání částice ve vzdálenosti \(x=15\ \mathrm{m}\) od zdroje.
a) Porovnáním s obecným tvarem rovnice postupné vlny zjišťujeme, že
- amplituda je \(y_\mathrm{m}=0{,}15\ \mathrm{m}\);
- \(2\pi/T=0{,}90\), takže perioda \(T=7{,}0\ \mathrm{s}\);
- \(2\pi/\lambda=0{,}31\), takže vlnová délka \(\lambda=20\ \mathrm{m}\).
Frekvence je převrácenou hodnotou periody \(f=1/T=0{,}14\ \mathrm{Hz}\).
Rychlost šíření vlny spočítáme pomocí vlnové délky \(v=\lambda/T=2{,}9\ \mathrm{m/s}\).
b) Do rovnice postupné vlny dosadíme za čas \(t=2\ \mathrm{s}\),
\[ y = 0{,}15\sin(1{,}8-0{,}31x) \]a vykreslujeme závislost \(y\) na \(x\). Použijte znalosti z matematiky.
Pokud byste přece jen váhali, doporučujeme následující „kuchařku“:
- nejdříve vyznačíme amplitudu 0,15 m (meze, v nichž sinusoida kmitá),
- poté vyznačíme vlnovou délku 20 m (vzdálenost, po níž se průběh křivky začne opakovat),
- vypočítáme výchylku \(y_0\) pro \(x=0\ \mathrm{m}\) (průsečík se svislou osou) – pozor, kalkulačka musí být přepnuta na radiány,
- vypočítáme výchylku \(y_1\) pro \(x=\lambda/4=5\ \mathrm{m}\) (čtvrtina periody),
- nakonec nakreslíme sinusoidu.
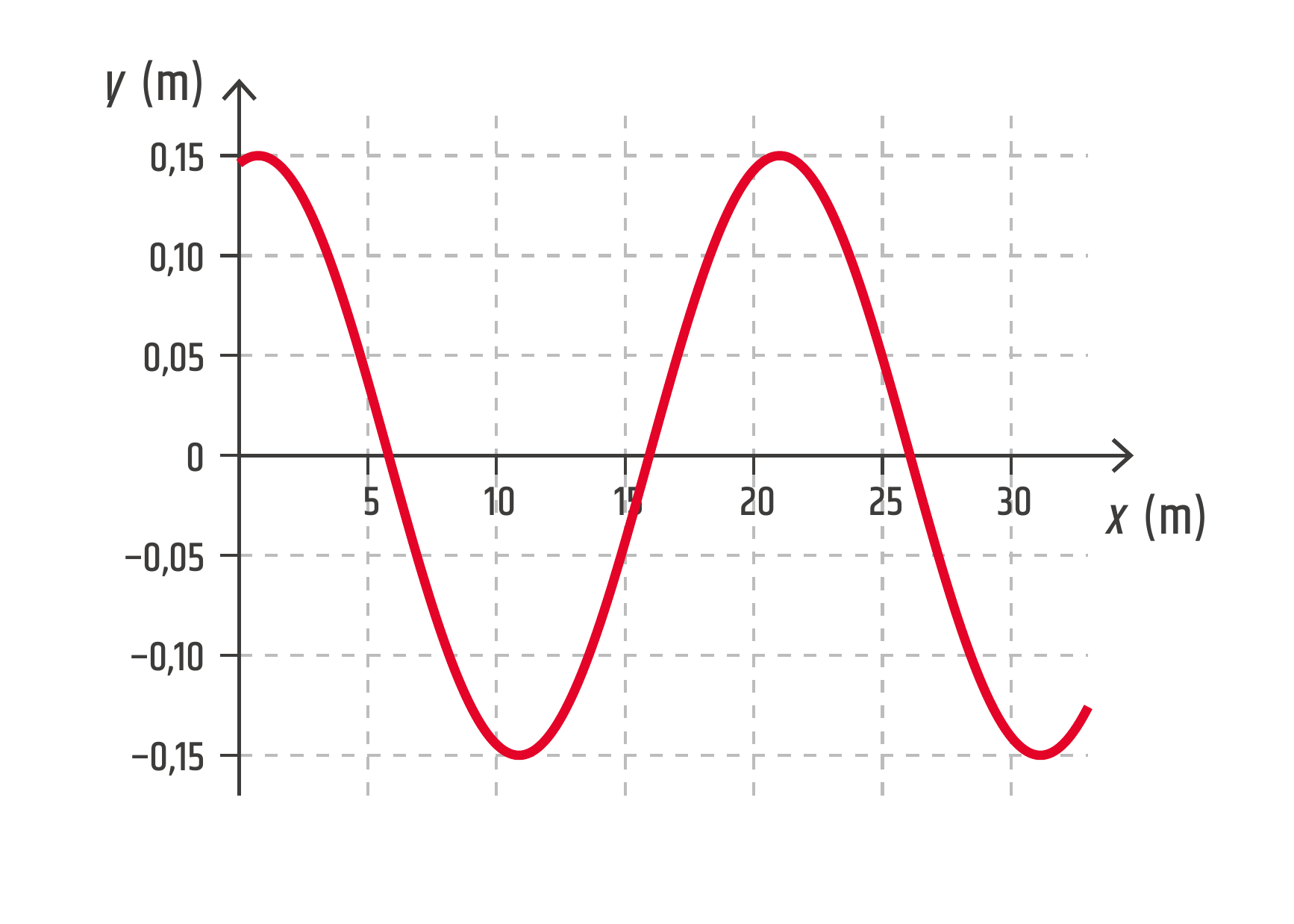
Zdroj
c) Do rovnice postupné vlny dosadíme vzdálenost \(x=15\ \mathrm{m}\),
\[ y = 0{,}15\sin(0{,}90t-4{,}65) \]a vykreslujeme závislost \(y\) na \(t\).
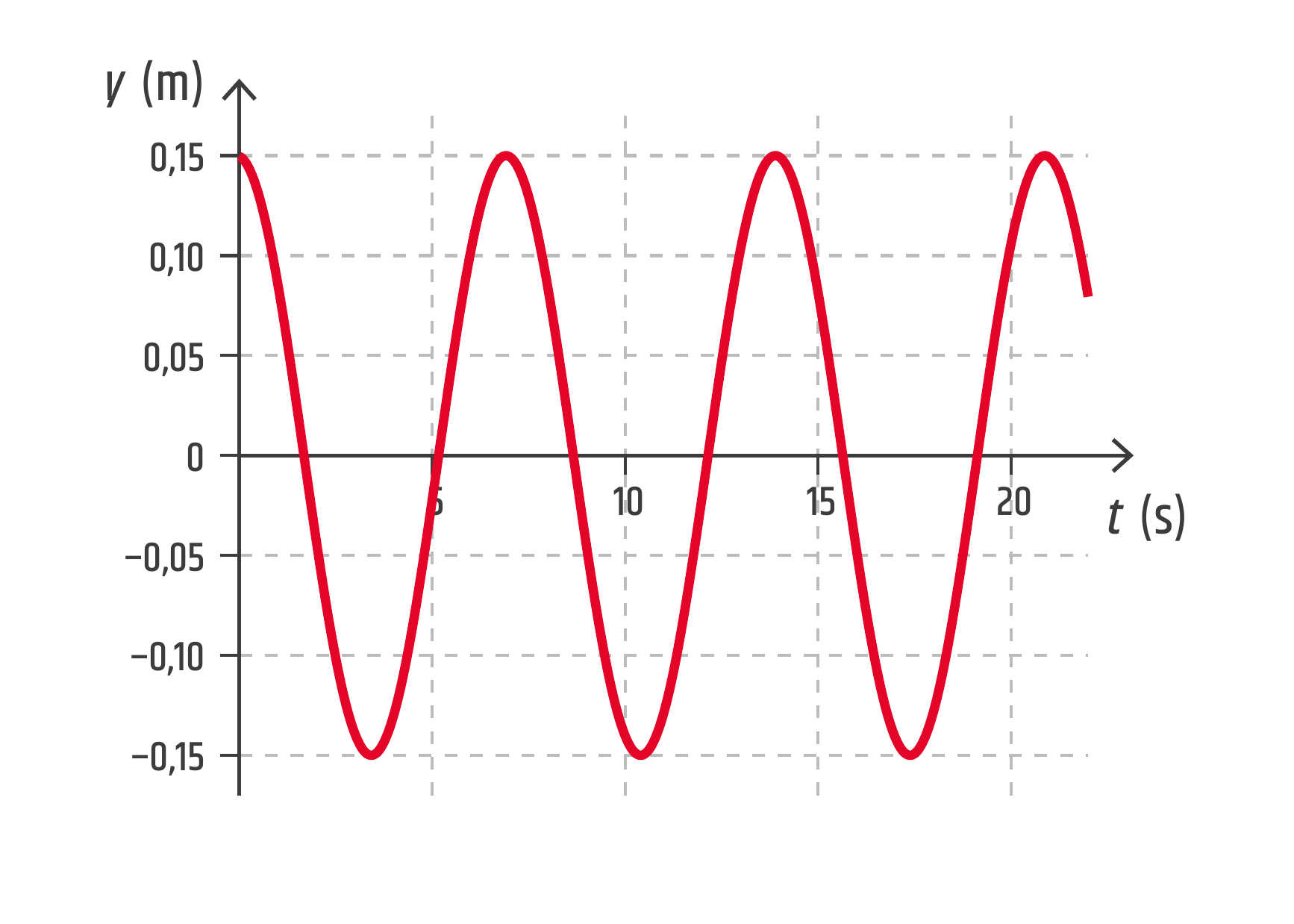
Zdroj

