Zvuk je mechanické vlnění, které vnímáme sluchem. V této části se podíváme na vlastnosti zvuku, jimiž se liší od ostatních mechanických vln.
Zdroj
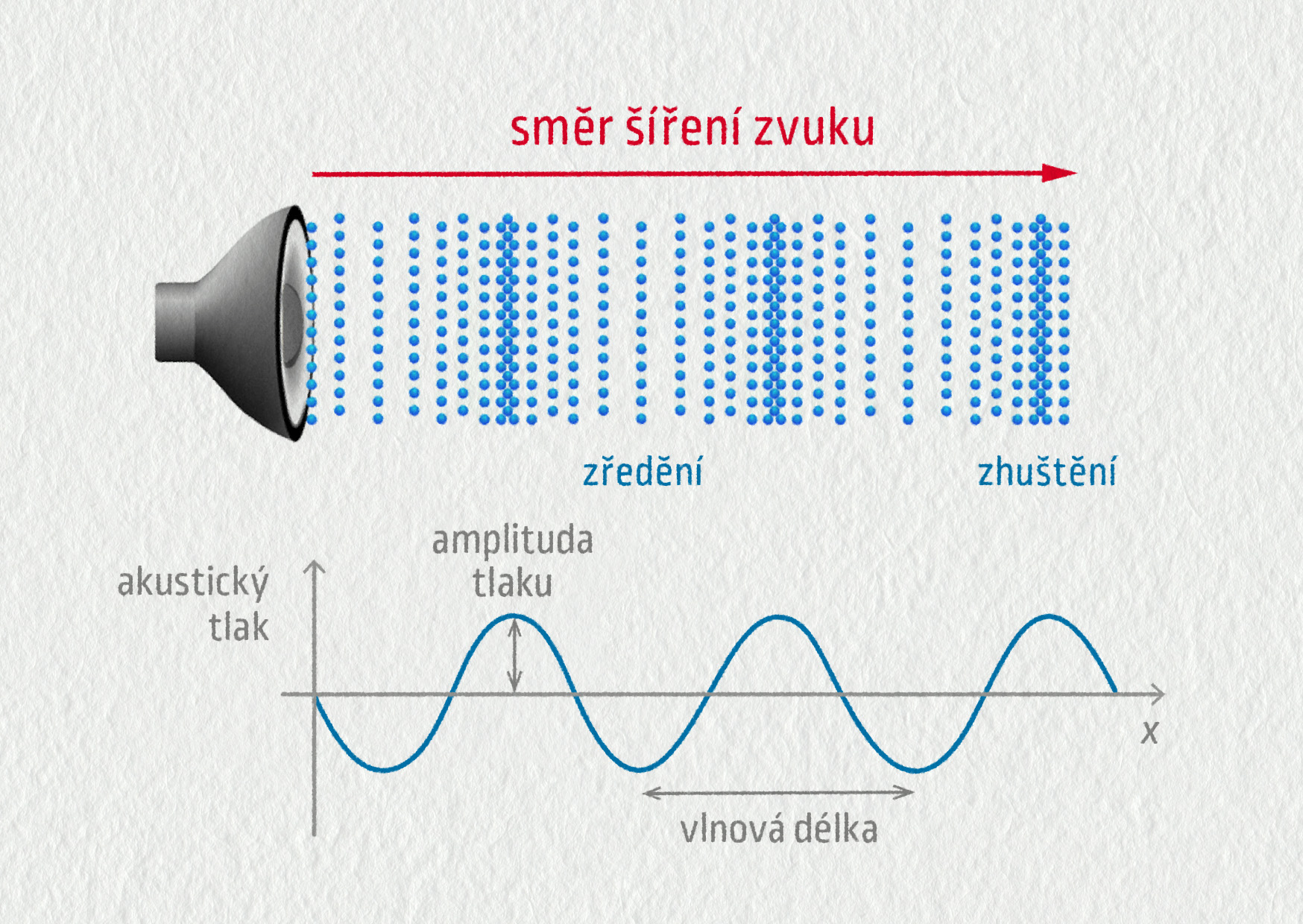
Zvuk vzniká kmitáním těles. Prohlédnout si to můžete v úvodním videu k této kapitole. Podle toho, zda je toto kmitání (a jím vyvolaná vlna) pravidelné či nikoli, rozlišujeme tóny a hluk (šum).
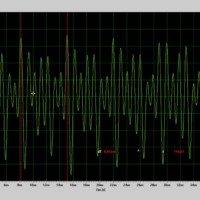
- Tón vzniká pravidelným kmitáním zdroje. Jelikož se kmitání zdroje periodicky opakuje, lze u něj i u odpovídající zvukové vlny určit periodu a frekvenci. U tónu lze určit výšku.
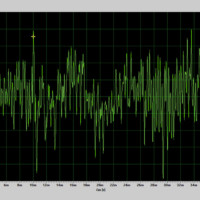
- Hluk vzniká nepravidelným kmitáním zdroje. Jelikož se kmitání neopakuje, perioda ani frekvence hluku neexistují. U hluku nelze určit výšku.
Porovnání tónu a hluku
Zdroj
Zdroj
Vlastnosti tónů
U každého tónu lze určit následující vlastnosti:
- výška,
- délka,
- hlasitost,
- barva.
Hudebníci dokáží tyto vlastnosti zaznamenat do notového zápisu a pak zpětně interpretovat. Jejich fyzikální podstatu nyní rozebereme podrobněji.
Výška tónu
Výška tónu je dána frekvencí odpovídající zvukové vlny. Platí jednoduchá souvislost: čím vyšší je frekvence, tím je tón vyšší.
Lidské ucho je citlivé na frekvence v intervalu přibližně od 20 Hz do 20 kHz, přičemž horní hranice je značně individuální a s věkem klesá (vyzkoušejte to pomocí generátoru signálů v mobilu). Zvuk o frekvencích nižších než 20 Hz se nazývá infrazvuk, zvuk o frekvencích vyšších než 20 kHz je ultrazvuk. Na rozdíl od psů, netopýrů, delfínů a některých dalších zvířat lidé ultrazvuk neslyší. Ultrazvuk se využívá v lékařství k diagnostice (sonografické vyšetření) a v technice (čištění povrchů, defektoskopie).
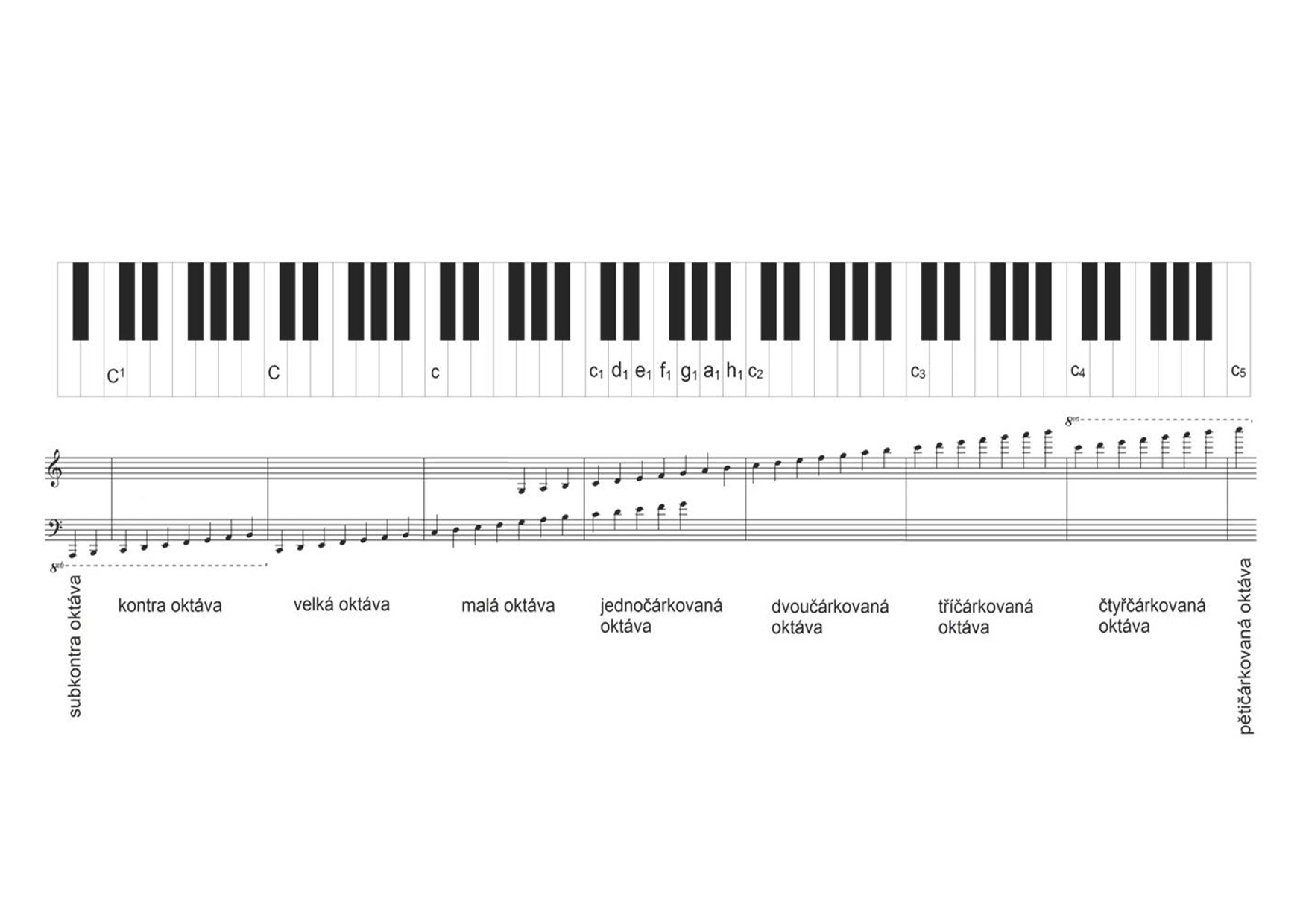
Hudebníci zapisují výšku tónu pomocí not – přesněji řečeno pomocí polohy hlavičky noty v notové osnově opatřené klíčem.
Zdroj
Význačné postavení má tón a1, tzv. komorní a o frekvenci 440 Hz. Podle něj se totiž ladí klavíry, smyčcové i symfonické orchestry. Rozdělení klávesnice do oktáv také není náhodné. Dva tóny vzdálené o jednu oktávu mají frekvence v poměru 2 : 1. Takže například tón a2 má frekvenci 880 Hz, tón a3 frekvenci 1760 Hz a tón A ve velké oktávě frekvenci 110 Hz. O hudebních intervalech a temperovaném ladění více v oddíle Hudební nástroje.
Interval frekvencí, které člověk dokáže zazpívat, je mnohem užší než interval slyšitelný, u amatérských zpěváků obvykle jen dvě oktávy. Výška hlasu dospělého člověka je ovlivněna růstem hlasivek v pubertě. Ženské hlasy (soprán, mezzosoprán, alt) jsou přirozeně vyšší než mužské (tenor, baryton, bas).
| Hlas | Rozsah tónů | Přibližný rozsah frekvencí |
|---|---|---|
| soprán | a–c3 | 220 Hz až 1 045 Hz |
| alt | e–f2 | 165 Hz až 700 Hz |
| tenor | c–a1 | 130 Hz až 440 Hz |
| bas | E–f1 | 82 Hz až 350 Hz |
Porovnání výšky vybraných hudebních nástrojů s lidským hlasem najdete na wikipedii.

Zdroj

Zdroj
Tón c3 není pro lidský hlas nepřekonatelnou mezí. Mnoho lidí dokáže zakvičet pořádně vysoko. Ale aby to byl tón, který má přesně danou výšku, jež patří do „písničky“, to vyžaduje spoustu tréninku. Jednu takovou výzvu nachystal sopranistkám Wolfgang Amadeus Mozart v opeře Kouzelná flétna. Ve slavné árii Královny noci zazní v obrovské rychlosti tón f3 o frekvenci bezmála 1 400 Hz. Tento tón leží na hranici lidských možností a jeho dosažení je svého druhu sportovní výkon (pomineme-li uměleckou složku). Mozart byl nejen geniální skladatel, ale své „řemeslo“ též dokonale ovládal. Proto zpěvačce nejdříve poskytne prostor, aby se rozezpívala, a druhou sloku ji nechá zazpívat v paralelní mollové tónině (o dva tóny níže), takže „kritické místo“ se napodruhé téměř vždy povede dokonale. Ve videu níže zpívá Diana Damrau árii Královny noci v opeře Kouzelná flétna Wolfganga Amadea Mozarta.
Délka tónu
Délka tónu je doba, po kterou tón zní. Fyzikálně tedy odpovídá času v sekundách (délce vlnového klubka). Hudebníci ji udávají v dobách. Kolik sekund odpovídá jedné době, naznačí autor slovně na začátku skladby. Například „allegro“ znamená přibližně 132 dob za minutu, „largo“ značí 46 dob za minutu… Tato souvislost není matematicky přesná a dává prostor pro mírně odlišné pojetí interpretace.
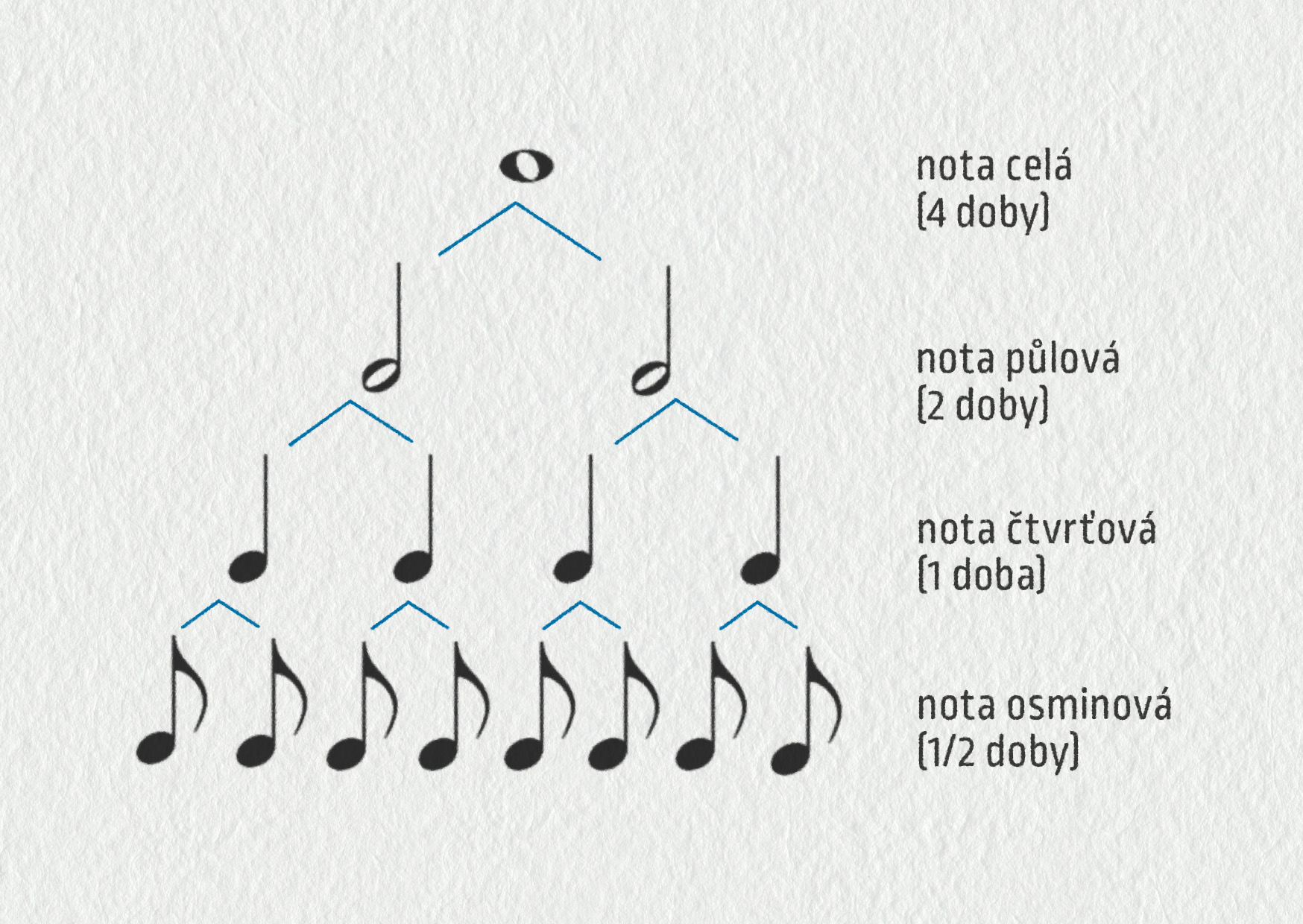
Zdroj
U dechových nástrojů (nebo zpěvu) trvá tón tak dlouho, dokud hudebníkovi nedojde dech. Záleží tedy na nástroji, na který se hraje, na kapacitě plic a taky hlasitosti tónu. U klavíru nebo kytary po počátečním impulzu hlasitost tónu přirozeně klesá k nule, obvykle se tón nedrží déle než osm dob. Naopak u varhan, kde vzduch do píšťal fouká čerpadlo, může znít tón opravdu hodně dlouho. Není proto divu, že nejdelší skladba na světě (někdo ji chápe jen jako recesi a za umění ji nepovažuje), pojmenovaná „As slow as possible“, je určena právě pro varhany. Po úvodní pomlce, která trvala rok a půl, zněl první akord úctyhodných 518 dní a celé „dílo“ se bude hrát dohromady 639 let.
Hlasitost tónu
Zatímco výšku a délku tónu vnímají všichni lidé přibližně stejně, vjem hlasitosti je velice subjektivní. Někdo slyší dopadnout špendlík, jiný neslyší ani tikot hodin. Pro někoho je hlasitá hudba příjemná a vzbuzuje v něm pocit uvolnění, u jiného vyvolávají tytéž hlasité zvuky napětí až fyzickou bolest.
Fyzikálně je hlasitost dána amplitudou kmitání prostředí, kudy se šíří zvuková vlna: větší amplituda znamená hlasitější zvuk. Protože se ovšem amplituda zvukového vlnění nesnadno měří, používají se k objektivnímu porovnávání hlasitosti veličiny intenzita zvuku \(I\) a hladina intenzity zvuku \(L\).
Intenzita zvuku \(I\) je definována jako podíl výkonu \(P\) přenášeného zvukovou vlnou a plochy \(S\), na niž dopadá zvuková vlna:
\[ I = \frac PS\;. \]Intenzita zvuku tedy číselně vyjadřuje, kolik energie přinesou zvukové vlny za sekundu na plochu 1 m2 (kolmou ke směru šíření). Jednotkou intenzity zvuku je watt na metr čtverečný (W/m2). Zdravý sluch dokáže při frekvenci 1 000 Hz zaregistrovat nejmenší intenzitu \(I_0=10^{-12}\ \mathrm{W/m}^2\). Této hodnotě se říká práh slyšení. Při intenzitách kolem 101 W/m2 je zvuk natolik hlasitý, že sluchový vjem přechází ve vjem bolesti. Proto se této hodnotě říká práh bolesti.
Předpokládejme, že reproduktor o zvukovém výkonu \(P_1=20\ \mathrm{W}\) vysílá zvukové vlny rovnoměrně do volného poloprostoru. Určete intenzitu zvuku \(I_1\) ve vzdálenosti \(r_1=50\ \mathrm{m}\) od reproduktoru a výkon \(P_2\), jaký v této vzdálenosti dopadá na ušní bubínek o ploše \(S_2=55\ \mathrm{mm}^2\).
Situace je znázorněna na obrázku 22.55, \(S_1\) zde značí polovinu povrchu koule. Intenzita zvuku \(I_1\) ve vzdálenosti \(r_1\) je podle definice
\[ I_1 = \frac{\hbox{výkon}}{\hbox{plocha}} = \frac{P_0}{S_1} = \frac{P_0}{2\pi r_1^2} = \frac{20\ \mathrm{W}}{15{,}7\cdot10^{-4}\ \mathrm{m}^2} = 1{,}27\cdot10^{-3}\ \mathrm{W/m}^2\;, \]což je dobře slyšitelný zvuk.
Na bubínek dopadá výkon
\[ P_2 = I_1\cdot S_2 = 1{,}27\ \mathrm{W/m}^2\cdot10^{-3} \cdot55\cdot10^{-6}\ \mathrm{m}^2 = 7{,}0\cdot10^{-8}\ \mathrm{W}\;. \]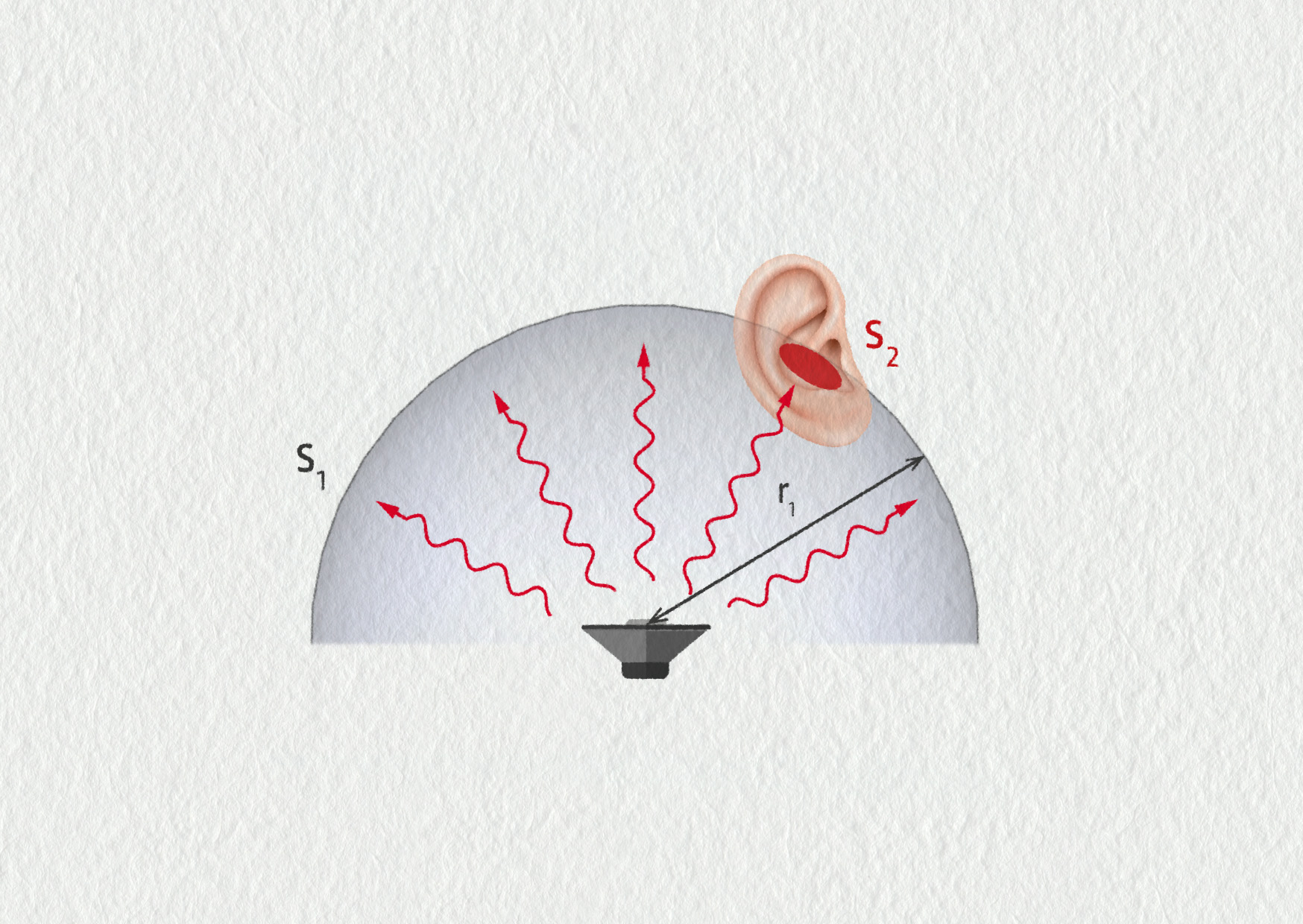
Zdroj
Intenzita zvuku je fyzikálně dobře pochopitelná veličina, ale bohužel neodpovídá tomu, jak hlasitost vnímá náš sluch. Když se totiž zvýší intenzita zvuku \(I\) na desetinásobek, nemáme pocit, že je zvuk desetkrát hlasitější. Spíše se ukazuje, že ucho se adaptuje podle aktuální hlasitosti. Ve zvýšení intenzity např. z 10−5 W/m2 na 10−4 W/m2 cítí stejný „krok“ jako ve zvýšení z 10−4 W/m2 na 10−3 W/m2 – řečeno prostě, ucho vnímá hlasitost logaritmicky. Proto je přirozené vyjadřovat hlasitost v logaritmické škále.
Hladina intenzity zvuku \(L\), vyjádřená v decibelech dB, je definována vztahem
\[ L = 10\log\frac{I}{I_0}\;, \]kde log je logaritmus o základu 10, \(I\) je intenzita zvuku v daném místě a \(I_0=10^{-12}\ \mathrm{W/m}^2\), což je dohodou stanovená referenční hodnota (odpovídající prahu slyšení při 1 000 Hz).
| Hladina intenzity zvuku | Příklad zvuku |
|---|---|
| 0 dB | práh slyšení |
| 20 dB | šum listí |
| 40 dB | déšť |
| 60 dB | běžný rozhovor |
| 80 dB | hlučný provoz na silnici |
| 90 dB | motorová sekačka na trávu |
| 110 dB | diskotéka |
| 130 dB | práh bolesti |
Při dlouhodobém poslechu (přestože nás nic nebolí) hrozí nebezpečí poškození sluchu pro hlasitosti vyšší jak 85 dB. Od hlasitosti vyšší jak 100 dB hrozí nebezpečí poškození sluchu v řádu minut.

Zdroj
Jeden zpěvák vyprodukuje v hledišti zvuk o hladině intenzity 65 dB.
- Jaká je odpovídající intenzita ve W/m2?
- Kolik decibelů dokáže vytvořit padesátičlenný pěvecký sbor? Předpokládejte, že všichni zpěváci zpívají stejně hlasitě a vzájemně se netlumí.
a) Nejelegantnějším postupem je vyjádřit neznámou \(I\) z rovnice \(L=10\log(I/I_0)\) a číselné hodnoty dosadit až v posledním kroku výpočtu. Pokud byste váhali, jak na to, nechte se inspirovat následujícím řešením s dosazenými číselnými hodnotami.
Podle zadání \(L_1=65\ \mathrm{dB}\), konstanta \(I_0=10^{-12}\ \mathrm{W/m}^2\) má stejnou hodnotu vždy, takže dosazením do definičního vztahu \(L_1=10\log(I_1/I_0)\) získáme rovnici pro neznámou intenzitu zvuku \(I_1\) odpovídající jednomu zpěvákovi
\[ 65=10\log\frac{I_1}{10^{-12}} \quad\hbox{neboli}\quad 6{,}5=\log\frac{I_1}{10^{-12}} \]Neznámá \(I_1\) se nachází v argumentu funkce logaritmus, proto využijeme definici logaritmu a rovnici „odlogaritmujeme“
\[ 10^{6{,}5} = \frac{I_1}{10^{-12}}\;, \]takže
\[ I_1 = 10^{6{,}5}\cdot10^{-12} = 10^{6{,}5-12} = 10^{-5{,}5} = 3{,}16\cdot10^{-6}\ \mathrm{W/m}^2\;. \]Intenzita zvuku vyvolaná jedním zpěvákem je \(3{,}16\cdot10^{-6}\ \mathrm{W/m}^2\).
b) Za předpokladu, že všichni zpěváci zpívají stejně hlasitě a vzájemně se netlumí, bude intenzita zvuku od padesáti zpěváků \(I_{50}=50I_1=1{,}58\cdot10^{-4}\ \mathrm{W/m}^2\). Tuto hodnotu přepočítáme na decibely:
\[ L_{50} = 10\log\frac{I_{50}}{I_0} = 10\log\frac{1{,}58\cdot10^{-4}}{10^{-12}} = 82\ \mathrm{dB}\;. \]Padesát zpěváků vyprodukuje v hledišti zvuk o hladině intenzity 82 dB.

Zdroj
Barva tónu
Na saxofon a housle mohou dva hudebníci zahrát tón stejné výšky stejně hlasitě, přesto i neškolený posluchač pozná, že vydávané zvuky nejsou stejné. Liší se totiž barvou – podíváme se nyní, v čem barva tónů fyzikálně spočívá.
Postupná zvuková vlna, která má sinusový průběh, představuje tak zvaný čistý tón. Je to právě ta nejjednodušší vlna, jejíž rovnici
\[ y = y_\mathrm{m}\sin\left[2\pi\left(\frac tT-\frac x{\lambda}\right)\right]\;. \]jsme odvodili na konci oddílu Vlnění. Je to vlna o jediné, přesně dané frekvenci \(f=1/T\). Čistý tón můžeme vytvořit nejjednodušeji, když připojíme střídavé napětí sinusového průběhu k reproduktoru. Je to tón, který slyšíte v klasickém telefonním sluchátku, a také tón, který vydává klasická kovová ladička. K čistému tónu má blízko též zvuk vydávaný flétnou.
Čistý tón
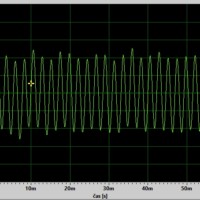
Zdroj
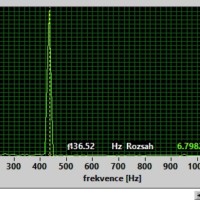
Zdroj
Barevný tón vzniká složením zvukových vln sinusového průběhu o frekvencích \(f\), \(2f\), \(3f\), \(4f\), … Frekvenci \(f\) (a jí odpovídající vlně) se říká základní frekvence (základní složka), frekvencím \(2f\), \(3f\), \(4f\), … (a jim odpovídajícím vlnám) se říká vyšší harmonické frekvence (vyšší harmonické složky). Podle základní frekvence \(f\) určuje lidské ucho výšku tónu. Barva tónu je dána zastoupením vyšších harmonických frekvencí ve výsledném tónu. Jinými slovy řečeno, zvuk jednotlivých hudebních nástrojů se liší tím, kolik a které vyšší harmonické frekvence tyto nástroje „přimíchávají“ k základnímu tónu. Proč jsou to právě násobky základní frekvence, vysvětlíme v následujícím oddíle Hudební nástroje.
Skládání většího počtu tónů si můžete vyzkoušet v animaci: pohybem červenými čtverečky měňte amplitudu příslušných vyšších frekvencí a poslouchejte, jak se mění barva tónu.
Podobně jako jste v předchozí animaci skládali barevný zvuk z čistých tónů, lze naopak barevný tón matematicky rozložit na součet čistých tónů. Graf vyjadřující zastoupení jednotlivých frekvencí v daném zvuku se nazývá spektrum zvuku. Rozklad můžeme provést automaticky pomocí aplikací na Fourierovou analýzu signálu (například programem Soundard Scope, který si vyzkoušíte v praktiku).
V animaci https://phyanim.sciences.univ-nantes.fr/Ondes/son/analyseur.php můžete porovnat barvu a odpovídající spektrum několika hudebních nástrojů.
Akord je souzvuk několika (barevných) tónů. Je to tedy směs vln o frekvencích \(f_1\), \(2f_1\), \(3f_1\), \(4f_1\), … (první tón), \(f_2\), \(2f_2\), \(3f_2\), \(4f_2\), (druhý tón), \(f_3\), \(2f_3\), \(3f_3\), \(4f_3\), (třetí tón) atd., přičemž \(f_1\), \(f_2\) a \(f_3\) mohou být libovolné. Aby se nám akord jevil jako libozvučný, musí být základní frekvence \(f_1\), \(f_2\) a \(f_3\) v poměru malých celých čísel.
Zdroje a detektory zvuku
Zdroj
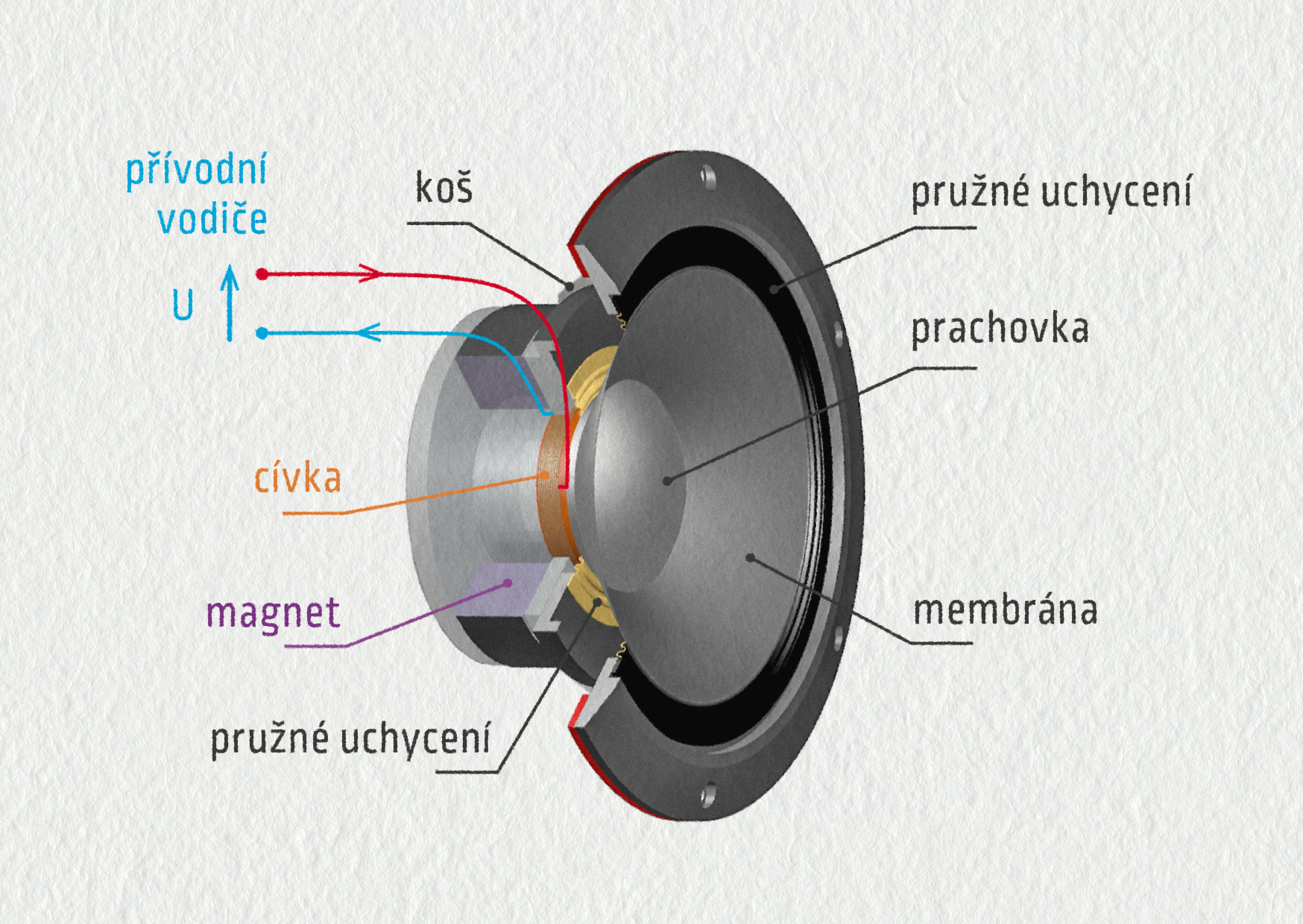
Reproduktor převádí kmitání elektrického napětí na mechanické kmitání o stejné frekvenci.
Na svorky reproduktoru přivedeme střídavé napětí. Cívkou začne protékat střídavý proud, a tím pádem bude vytvářet střídavé magnetické pole. Poněvadž se poloha severního a jižního magnetického pólu cívky střídá, je střídavě přitahována a odpuzována magnetickým polem permanentního magnetu, což způsobí její kmitavý pohyb. Cívka je spojena s membránou reproduktoru, která se tímto mechanismem dává do pohybu a rozkmitává okolní molekuly vzduchu. Molekuly vzduchu si kmitáním předávají energii a do prostoru se šíří zvuková vlna.
Kromě popsaného nejběžnějšího reproduktoru založeného na elektrodynamickém principu existují i reproduktory elektrostatické (používané ve sluchátkách) nebo piezoelektrické (jsou levné a používají se pro vyšší frekvence).
Zdroj
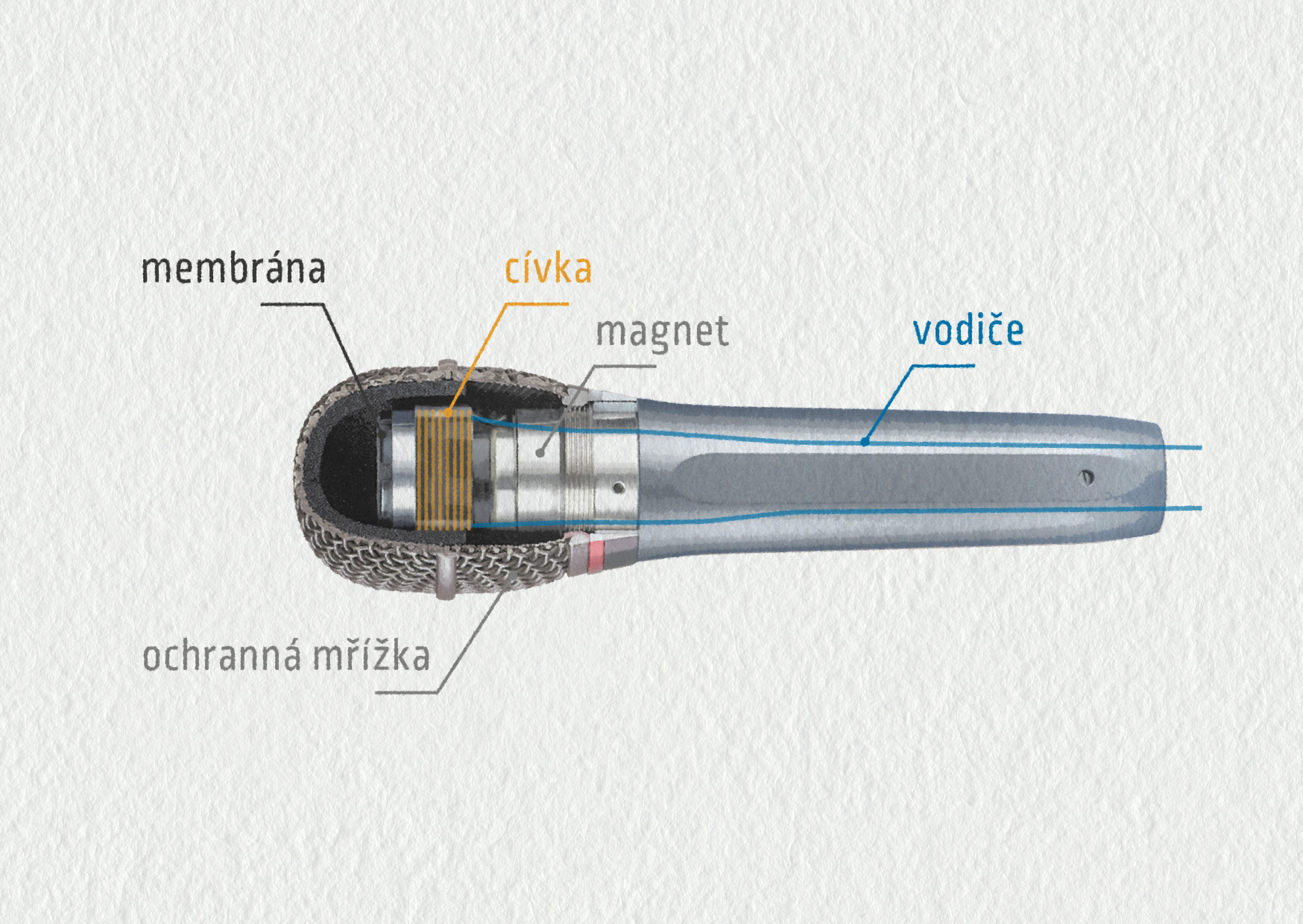
Mikrofon převádí mechanické kmitání na kmitání elektrického napětí o stejné frekvenci. Jde vlastně o obrácený princip reproduktoru. Zvukové vlny dopadají na membránu a rozkmitávají ji. Membrána je spojena s cívkou, která se střídavě pohybuje dovnitř a ven z magnetického pole vytvořeného permanentním magnetem. Magnetické pole uvnitř cívky se tedy mění a elektromagnetickou indukcí na jejích svorkách vzniká střídavé napětí.
Kromě popsaného dynamického membránového mikrofonu se používají i mikrofony kondenzátorové (jeden najdete v galerii 18.33), elektretové a piezoelektrické.
Zdroj
Zdroj
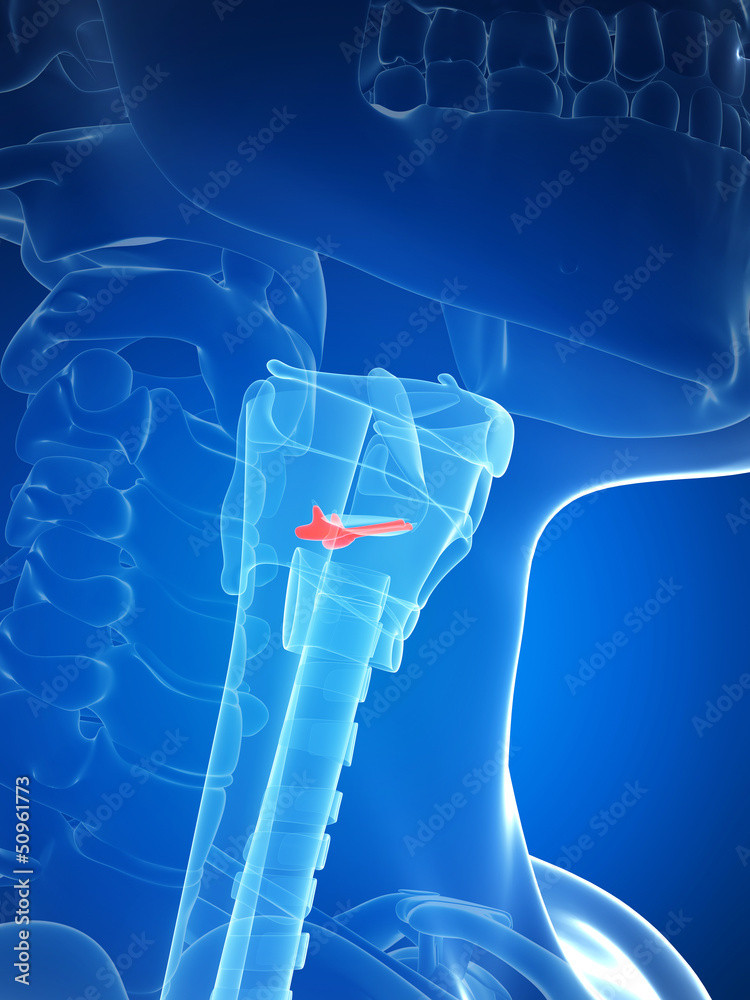
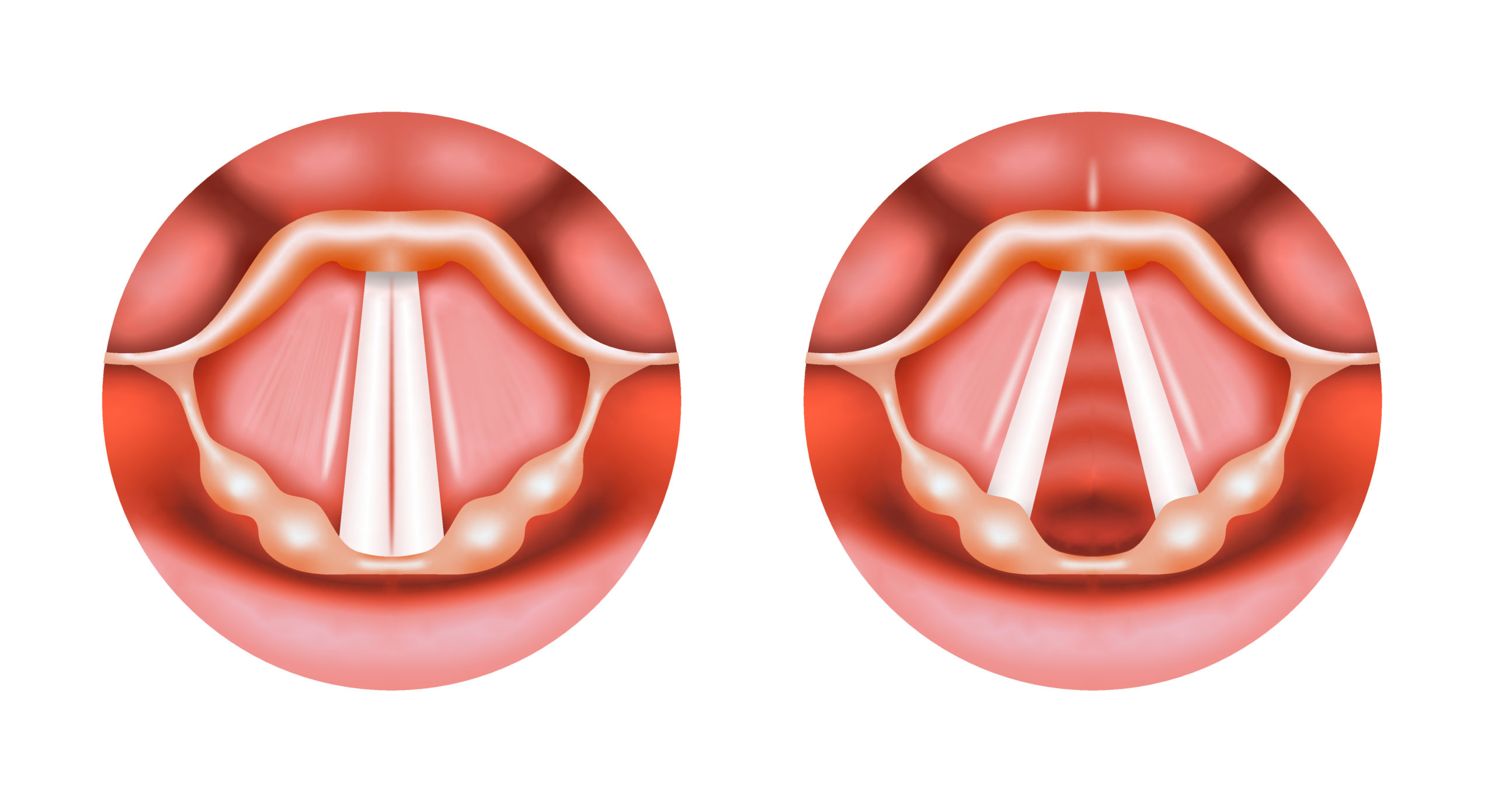
Hlasivky jsou uloženy v hrtanu. Hlasové ústrojí je tvořeno dvojicí pružných vazů, jejichž napětí dokážeme ovládat vůlí přes hlasivkové svaly. Při dýchání jsou hlasivky povolené a vzniklou štěrbinou mezi nimi může vzduch volně procházet. Při mluvení nebo zpívání se hlasivky napnou tak, že k sobě těsně přiléhají. Proud vzduchu z plic spolu s napětím hlasivek způsobí velice rychlé pootevírání a zpětné zavírání štěrbiny mezi nimi, čímž vznikají tlakové vlny, které vnímáme jako zvuk. Frekvence otevírání a zavírání hlasivkové štěrbiny je zřejmě frekvencí generovaného zvuku.
Poznamenejme, že vzniklý zvuk rezonuje v tělních dutinách (ústní, nosní, lebeční, hrudní koš), čímž získává zabarvení charakteristické pro daného člověka.
Zdroj
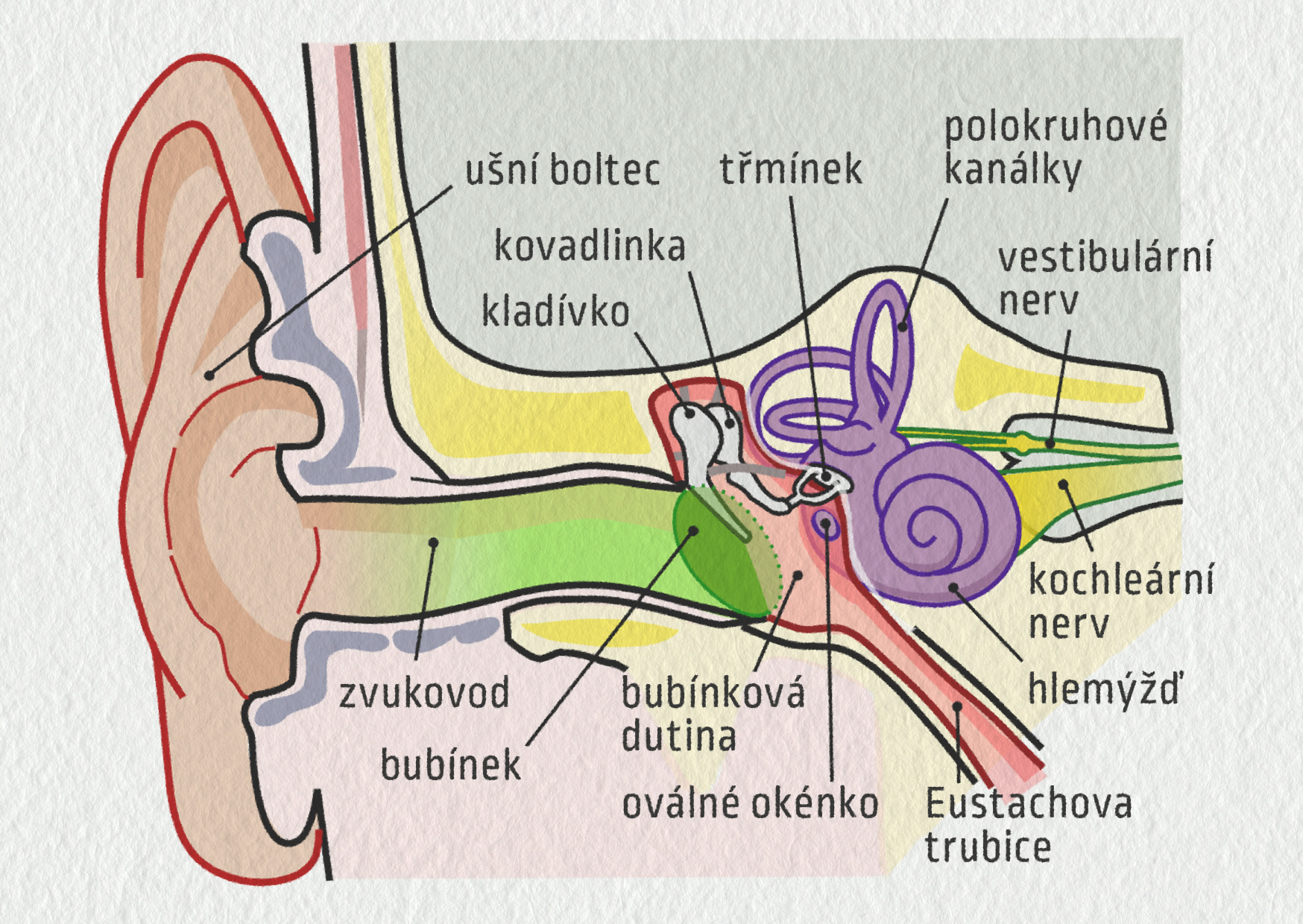
Lidské ucho se podle podoby šíření zvukového signálu rozděluje na tři části – vnější, střední a vnitřní ucho.
Vnější ucho je tvořeno boltcem a zvukovodem. Na rozdíl od některých zvířat u člověka se postupně vytratila schopnost nasměrovat boltec na požadovaný zdroj zvuku a omezit tak příjem vln z jiných směrů. Zvuková vlna se šíří vzduchem vyplňujícím zvukovod a dopadá na bubínek. Bubínek je tenoučká membrána, která má tloušťku přibližně 0,1 mm a průměr do 1 cm a odděluje vnější a střední ucho.
Bubínek se tedy zvukovou vlnou rozkmitá a jeho kmitání se ve středním uchu přenáší pákovým mechanismem třemi nejmenšími kůstkami v těle – kladívkem, kovadlinkou a třmínkem – na oválné okénko labyrintu. Při tom dochází k zesílení tlaku (\(F=pS\)): bubínek má velkou plochu a tlak vzduchu na jeho vnější straně kmitá s malou amplitudou, naopak oválné okénko má malé rozměry a tlak kapaliny na jeho vnitřní straně kmitá s velkou amplitudou.
Ve vnitřním uchu se vibrace tlaku přenáší kapalinou (endolymfou) k membráně Cortiho orgánu obsahující vláskové buňky. Vláskové buňky jsou uspořádány tak, že každá oblast vnitřního ucha je citlivá na určitou frekvenci. Do mozku pak z ucha přichází signál o tom, které frekvence jsou ve zvuku zastoupeny a jak silně.
Zdroj
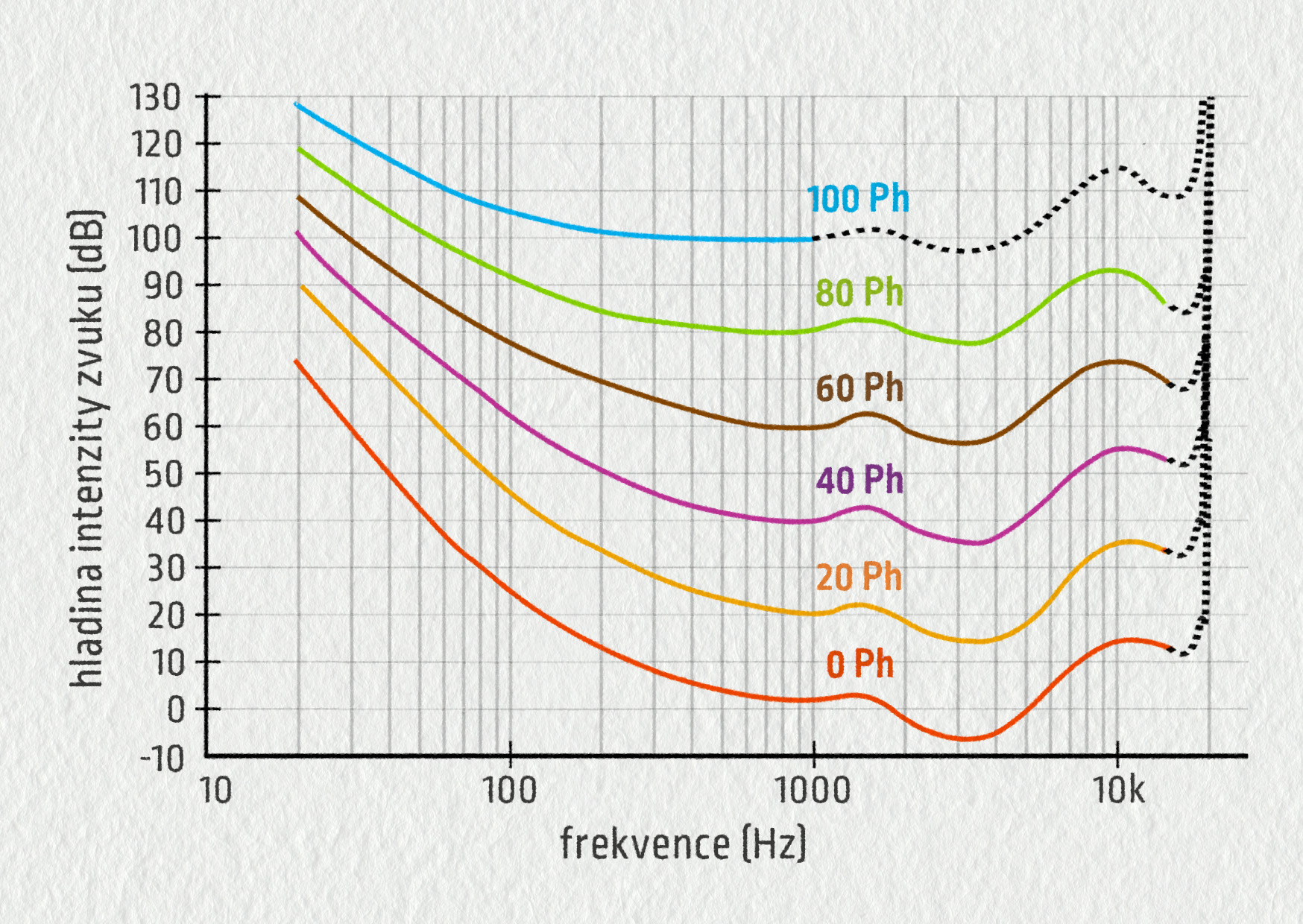
Na základě předchozího grafu 22.65 rozhodněte, pro kterou frekvenci zvuku je subjektivně vnímaná hlasitost ve fónech číselně rovna hladině intenzity zvuku v dB. Zapište celočíselnou hodnotu frekvence v kHz.
Fón (Ph) je jednotkou (subjektivně vnímané) hladiny hlasitosti. Hladina hlasitosti ve fónech je při frekvenci 1 kHz číselně rovna (objektivně měřitelné) hladině intenzity zvuku v dB. Pro jiné frekvence se hodnoty těchto veličin liší, neboť lidské ucho není na různé frekvence stejně citlivé.
Na základě předchozího grafu 22.65 rozhodněte, na kterou frekvenci zvuku je lidský sluch nejcitlivější? Zapište celočíselnou hodnotu frekvence v kHz.
Možná není náhodou, že frekvence dětského pláče se pohybuje v oblasti maximální citlivosti lidského sluchu.

