Eulerova metoda

Při studiu volného pádu narážíme na skutečnost, že podmínky volného pádu (na těleso působí pouze tíhová síla) lze poměrně těžko nastavit. Obvykle těleso padá ve vzduchu, a tudíž na něj působí kromě tíhové síly ještě odpor vzduchu, případně vztlaková síla. Pojďme se detailněji podívat, jak řešit situace, kdy se některá z působících sil mění v čase.

Úkoly:

Vyjmenujte a připomeňte vlastnosti všech sil, které působí na ledovou kroupu o poloměru 3,0 mm padající ve vzduchu z výšky 700 m.
Pomocí Newtonových zákonů určete velikost zrychlení.
Za pomoci počítače a tabulkového procesoru modelujte graf rychlosti v závislosti na čase.
Z grafu určete maximální rychlost pohybu kroupy.
Jaké parametry ovlivňují maximální rychlost kroupy?
Jaký je vliv vztlakové síly vzduchu? Můžeme ji zde zanedbat? Svou odpověď potvrďte výpočtem.
Dokážete odpovědět, jestli penny hozená z Empire State Building může zabít člověka na zemi? Zdůvodněte.

Řešení:

1) Jak vidíme z nákresu, na kroupu budou působit tři síly: tíhová \(\Vec{F}_\mathrm{G}\), odpor vzduchu \(\Vec{F}_\mathrm{O}\) a vztlaková \(\Vec{F}_\mathrm{VZ}\). Vztlakovou sílu zatím neuvažujme. K jejímu vlivu se vrátíme v otázce č. 6. Tíhová síla působí svisle dolů, pro její velikost platí \(F_\mathrm{G}=mg\). Má tedy konstantní velikost. Odpor vzduchu působí proti pohybu, v našem případě tedy svisle vzhůru, a má velikost \(F_\mathrm{O}=\frac{1}{2}C\varrho Sv^2\). Její velikost je tedy přímo úměrná druhé mocnině rychlosti \(F_\mathrm{O}=kv^2\), a bude se tedy po nějakou dobu zvětšovat. Veličina C je odporový koeficient; budeme-li uvažovat, že kroupa má tvar ideální koule, pak C = 0,50. Hustota vzduchu je na povrchu Země a při teplotě 15 °C přibližně 1,21 kg/m³. Budeme považovat i tuto veličinu pro zjednodušení za konstantní. S značí příčný průřez kroupy, který vypočítáme z poloměru r pomocí vzorce \(S=\pi r^2\).

2) Pro sestavení pohybových rovnic si nejprve zapíšeme počáteční podmínky a poté použijeme 2. Newtonův zákon:

Počáteční podmínky: \(y_0=700\ \mathrm{m}\), \(v_0=0\ \mathrm{m/s}\).

Aplikace 2. Newtonova zákona:

\[ \begin{aligned} ma&=mg-kv^2\\ m\,\frac{\mathrm{d}v}{\mathrm{d}t}&=mg-kv^2\\ a&=\frac{\mathrm{d}v}{\mathrm{d}t}=g-\frac{k}{m}v^2 \end{aligned} \]

Sestavili jsme rovnici, ve které vidíme, že velikost zrychlení kroupy je závislá na druhé mocnině její rychlosti. Čím je větší rychlost, tím je menší hodnota zrychlení, a tím méně rychlost narůstá. Pohyb kroupy tedy není rovnoměrný jako v případě volného pádu (bez odporových sil). Takové rovnici, ve které vystupuje zároveň fyzikální veličina a její derivace, říkáme diferenciální rovnice. V tomto případě jde o diferenciální rovnici prvního řádu (1. derivace rychlosti). Existují metody, kterými se dají takové rovnice řešit, my se podíváme na numerickou Eulerovu metodu řešení, kterou si sami můžeme simulovat na počítači. Na základě tohoto řešení pak zodpovíme všechny položené otázky.

3) Z kinematiky víme, že při pohybu rovnoměrně zrychleném je rychlost v libovolném čase \(v(t)=v_0+at\). Tentokrát se však velikost zrychlení mění, protože závisí na rychlosti. Vztah ovšem můžeme přibližně použít pro krátké časové úseky \(\Delta t\), za které se zrychlení a téměř nezmění. Za krátký čas \(\Delta t\) se tedy rychlost změní o \(a\cdot\Delta t\):

\[ v(t+\Delta t)=v(t)+a(t)\cdot\Delta t \]

A to je základ Eulerovy metody. V každém časovém okamžiku spočítáme zrychlení z aktuální rychlosti

\[ a=g-\frac{k}{m}v^2\;. \]

Rychlost, kterou bude mít kámen o \(\Delta t\) později, dostaneme přičtením \(a\cdot\Delta t\) k současné rychlosti. A posuneme se v čase o \(\Delta t\) vpřed. Nyní můžeme vypočítat zrychlení v novém, o něco pozdějším čase, a tak stále dokola, dokud nás to baví. Počítač to asi vydrží bavit déle, ale předvedeme si aspoň, jak proběhne několik prvních kroků, když si zvolíme časový krok \(\Delta t=0{,}05\ \mathrm{s}\) (přesnost metody závisí na kroku – čím kratší, tím je přesnější, ale tím víc se napočítáme). Pro zjednodušení se hodí spočítat si předem \(k/m=0{,}0838\ \mathrm{m^{-1}}\) jako novou konstantu.

Na začátku je \(v_0=0\), \(t_0=0\). Zrychlení je tedy rovno \(a_0=g-(k/m)v_0^2=9{,}81-0{,}0838\cdot0^2=9{,}81\ \mathrm{m/s^2}\). Z toho dostaneme rychlost v čase \(t_1=\Delta t=0{,}05\ \mathrm{s}\) jako \(v_1=v_0+a_0\cdot\Delta t=0+9{,}81\cdot0{,}05=0{,}4905\ \mathrm{m/s}\).
V čase \(t_1=0{,}05\ \mathrm{s}\) je \(v_1=0{,}4905\ \mathrm{m/s}\). Zrychlení je tedy rovno \(a_1=g-(k/m)v_1^2=9{,}81-0{,}0838\cdot0{,}4905^2=9{,}78972\ \mathrm{m/s^2}\). Z toho dostaneme rychlost v čase \(t_2=2\Delta t=0{,}1\ \mathrm{s}\) jako \(v_2=v_1+a_1\cdot\Delta t=0{,}4905+9{,}7892\cdot0{,}05=1{,}466438\ \mathrm{m/s}\).
V čase \(t_2=0{,}10\ \mathrm{s}\) spočítáme zrychlení \(a_2=g-(k/m)v_2^2=9{,}729047\ \mathrm{m/s^2}\). Z něj dostaneme rychlost \(v_3\) v čase \(t_3=0{,}15\ \mathrm{s}\), a tak dále.

Porovnáme-li několik prvních hodnot rychlosti, zjistíme, že kroupa bude zrychlovat. Při pohledu na zrychlení vidíme, že se postupně zmenšuje, a pohyb tudíž bude nerovnoměrně zrychlený a nárůst rychlosti bude stále menší a menší. Z čehož lze usoudit, že se nakonec takový pohyb stane rovnoměrným a kroupa dosáhne své maximální rychlosti, při které se vyrovnají obě síly, které na ni působí. Tíhová síla, která ji urychluje, bude stejně velká jako odporová síla, jejíž velikost postupně rostla s rostoucí rychlostí.

Zkusme si tyto výpočty provést v Excelu nebo jiném tabulkovém kalkulátoru a modelujme graf rychlosti v závislosti na čase. Nejprve nastavme časový krok, ve kterém budeme počítat a zobrazovat jednotlivé hodnoty rychlosti a zrychlení. Zde ho značíme dt a zvolili jsme hodnotu 0,05 s. Tíhové zrychlení má hodnotu g = 9,81 N/kg.

Koeficient odporu k je vypočítán z parametrů kroupy vztahem \(k=\frac{1}{2}C\varrho S\) (viz tabulka č.2)

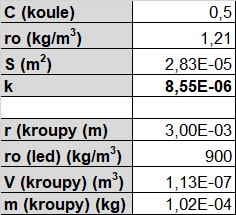
Pro výpočet rychlosti kroupy v každý časový okamžik je důležité zadat vzorec ve tvaru

\[\mathrm{B3} = \mathrm{B2} + \left(g - \frac{k}{m}*\mathrm{B2}*\mathrm{B2}\right)\cdot\mathrm{d}t\]

do odpovídající buňky tabulky (v naší ukázce B3).

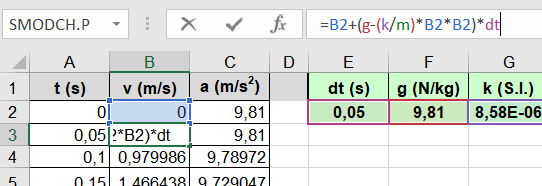
Tento vzorec poté můžeme zkopírovat na ostatní buňky v tabulce. Pokud chceme ještě vidět, jak se mění hodnota zrychlení, můžeme si ve vedlejším sloupci zadat vzorec pro jeho výpočet, ale není to nutné.

4) Pro dané hodnoty následně sestrojíme graf závislosti rychlosti na čase \(v=f(t)\).

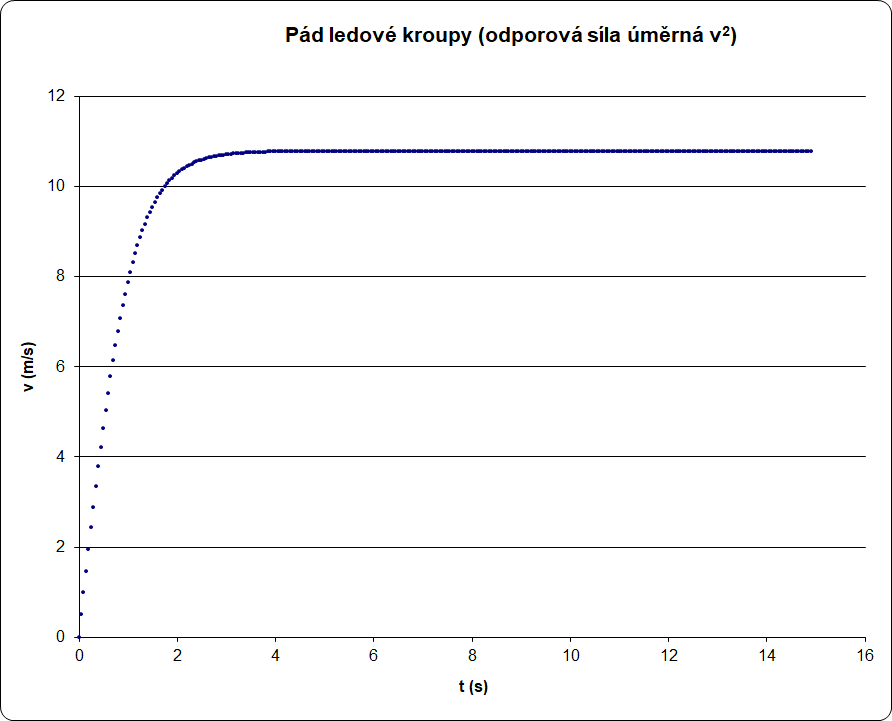
Z grafu pak můžeme určit, že ledová kroupa dosáhne maximální rychlosti přibližně v čase \(t=3\ \mathrm{s}\) a maximální rychlost má velikost \(v_\mathrm{max}=10{,}8\ \mathrm{m/s}\). Její hodnotu může také ověřit vztahem

\[v_\mathrm{max} = \sqrt{\frac{2mg}{C\varrho S}} = 10{,}8\ \mathrm{m/s} \]

který odvozujeme na základě rovnosti tíhové a odporové síly po určité době pohybu.

5) Jaké parametry ovlivňují maximální rychlost kroupy? V daném modelu můžete měnit rozměry kroupy a určovat, za jak dlouho dosáhne své maximální rychlosti a jakou hodnotu bude tato rychlost mít. Pozor, jde o model, ne vždy musí daná simulace odpovídat skutečnosti. Několik příkladů můžete najít v následujícím porovnání:

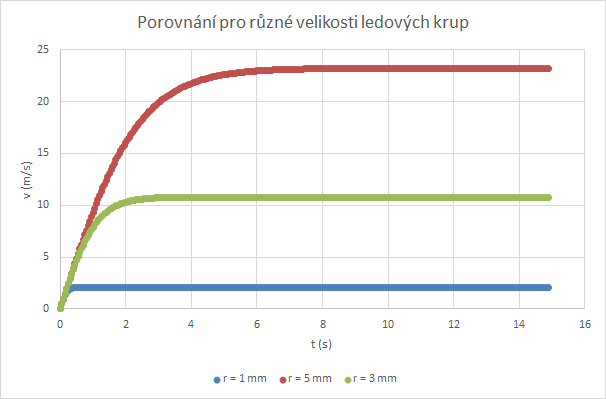
6) Co se týče vlivu vztlakové síly, vzhledem k hustotě vzduchu a rozměrům samotné kroupy jsme ji v našich výpočtech zanedbávali. Její velikost je \(F_\mathrm{VZ}=1{,}34\cdot10^{-6}\ \mathrm{N}\), zatímco \(F_\mathrm{G}=1{,}00\cdot10^{-3}\ \mathrm{N}\). Je přibližně 1000krát menší než tíhová síla, a pohyb kroupy proto příliš neovlivňuje. Její zanesení do modelu by pouze komplikovalo zápis rovnic.

Pro nadšence programování uvádíme výše uvedený postup v Pythonu: