Simulace soustavy částic
Úkol: Pomocí simulace sledujte vývoj soustavy částic.
Vybavení: program pro vytváření fyzikálních simulací Algodoo (freeware, ke stažení na http://www.algodoo.com), soubor Rozdeleni.phz.
Spusťte program Algodoo a otevřte v něm soubor Rozdeleni.phz. Tento soubor modeluje krabici s přepážkou, kde v jedné části krabice je plyn (40 částic), druhá část je prázdná. Model se spouští tlačítkem „Play“ v dolní části obrazovky, zastavit jej můžete tlačítkem „Pause“. Žlutou závoru uprostřed přepážky odstraníte tak, že na ni kliknete a stisknete klávesu „Delete“.
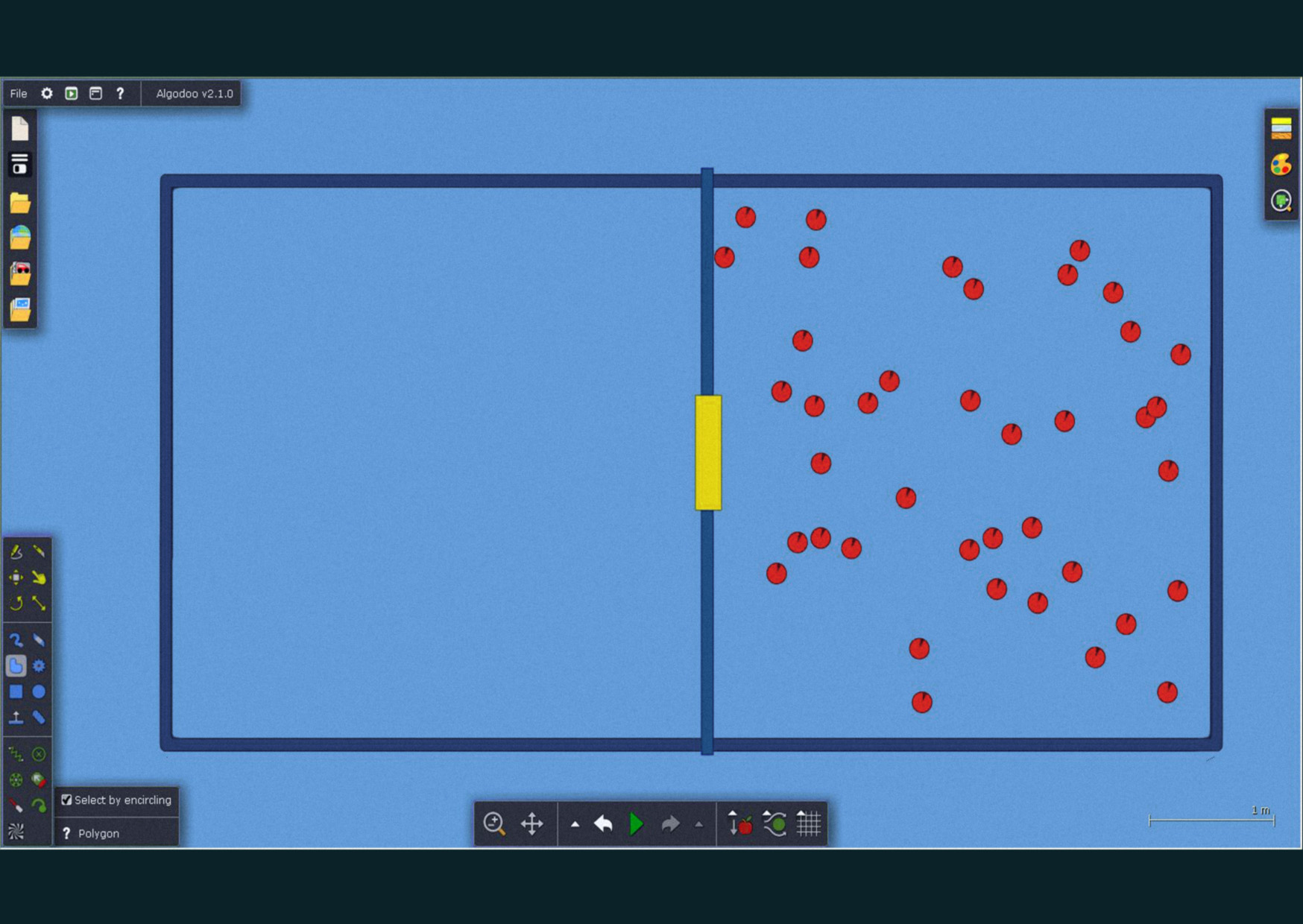
Zdroj
Stav soustavy ihned po odstranění přepážky má nízkou entropii, plyn může konat práci rozpínáním do levé části krabice. Částice přecházejí do levé části a některé se vracejí zpět do pravé části. Po chvíli se ale rozmístí vcelku rovnoměrně do obou částí krabice – tohle je nejpravděpodobnější stav plynu, stav s největší entropií. Plyn už není schopen konat práci, i když jednotlivé částice energii mají.
Pravděpodobnost konkrétního stavu (tj. rozdělení částic do levé a pravé části krabice) je dána tím, kolika způsoby je možné tento stav vytvořit (tento počet označíme jako \(W\)). Pokud jsou všechny částice v jedné části krabice, je to jenom jedna možnost (ta nejméně pravděpodobná). Jak to můžeme spočítat u jiných stavů?
Představte si stav, kdy vlevo je 10 částic a vpravo 30. Pro vytvoření tohoto stavu musíme rozmístit 40 částic. Předpokládejme, že je dokážeme rozlišit (třeba jsou očíslované). První z částic můžeme umístit na 40 pozic, druhou už jenom na 39 (první pozice už je obsazená), třetí na 38, … Celkově je to \(40\cdot39\cdot38\cdot\dots\cdot3\cdot2\cdot1=40!\) (čtyřicet faktoriál) možností. To by platilo u rozlišitelných částic. Částice v modelu ale nerozlišujeme. Proto musíme výsledek vydělit 10! (všechny možnosti umístění vybraných částic v levé části krabice) a 30! (v pravé části). Dostáváme výsledek \(W=40!/(10!\cdot30!)=847\,660\,528\). Je vidět, že tento stav má nesrovnatelně větší pravděpodobnost vzniku než stav se všemi částicemi na jedné straně.
Poznámka: Výpočet lze provést také pomocí kombinačních čísel.
Obecně platí, že pokud máme v krabici \(N\) částic a v její levé části je \(n\) částic (tj. v pravé části je jich \(N-n\) ), je počet možností, jak tento stav může vzniknout,
\[ W = \frac{N!}{n!\,(N-n)!}\;. \]S ohledem na to, že vycházejí obrovská čísla, pracuje se s přirozeným logaritmem počtu možností (logaritmováním se z velkých čísel stávají čísla uživatelsky přívětivější).
Postup měření:
- Spusťte soubor v Algodoo.
- Odstraňte závoru. Po 5 sekundách stopněte model a spočítejte, kolik částic je v levé a v pravé části krabice.
- Měření opakujte po 5 s alespoň 20krát.
- U každého změřeného stavu vypočítejte počet možností tohoto stavu \(W\).
- Vytvořte graf závislosti \(\ln W\) na čase.
Otázky:
- Jak se změní výsledný graf, když závoru v přepážce neodstraníte, ale pouze posunete tak, aby vznikl menší otvor než předtím?
- Jak se bude systém chovat, když se zvýší počet částic v modelu?
- Odhadněte na základě výpočtu, kolik je v učebně fyziky molekul.
- Jaká je pravděpodobnost toho, že se vzduch v učebně samovolně natlačí pouze do jedné poloviny místnosti?
- Jaké musí být mechanické vlastnosti kuliček a krabice v modelu, aby model odpovídal chování plynu?
Vzorové měření
| \(t\) (s) | \(n_1\) | \(n_2\) | \(W\) | \(\ln W\) |
|---|---|---|---|---|
| 0 | 0 | 40 | 1 | 0,0 |
| 5 | 6 | 34 | 3838380 | 15,2 |
| 10 | 4 | 36 | 91390 | 11,4 |
| 15 | 6 | 34 | 3838380 | 15,2 |
| 20 | 10 | 30 | 847660528 | 20,6 |
| 25 | 13 | 27 | 12033222880 | 23,2 |
| 30 | 16 | 24 | 62852101650 | 24,9 |
| 35 | 15 | 25 | 40225345056 | 24,4 |
| 40 | 16 | 24 | 62852101650 | 24,9 |
| 45 | 13 | 27 | 12033222880 | 23,2 |
| 50 | 16 | 24 | 62852101650 | 24,9 |
| 55 | 20 | 20 | 137846528820 | 25,6 |
| 60 | 20 | 20 | 137846528820 | 25,6 |
| 65 | 21 | 19 | 131282408400 | 25,6 |
| 70 | 21 | 19 | 131282408400 | 25,6 |
| 75 | 23 | 17 | 88732378800 | 25,2 |
| 80 | 21 | 19 | 131282408400 | 25,6 |
| 85 | 21 | 19 | 131282408400 | 25,6 |
| 90 | 21 | 19 | 131282408400 | 25,6 |
| 95 | 23 | 17 | 88732378800 | 25,2 |
| 100 | 19 | 21 | 131282408400 | 25,6 |
| 105 | 18 | 22 | 113380261800 | 25,5 |

