Člověk od pradávna hledal způsob, jak si zjednodušit život. Zejména pokud šlo o množství těžké mechanické práce, kterou musel vykonávat. Spoléhal se přitom na práci otroků, zvířat, vody a větru. Tyto zdroje nebyly příliš výkonné ani spolehlivé.

Zdroj
Zásadní změna přišla koncem 18. století s vynálezem parního stroje. Byl to první stroj, který ke svému pohonu využíval teplo. Dostupný zdroj energie umožnil průmyslovou revoluci a zcela změnil fungování naší civilizace. Zatímco konstruktéři zdokonalovali své stroje na základě pokusů a zkušeností, fyzikové se snažili nalézt obecné zákonitosti, které platí pro tepelné děje. Vznikl tak úplně nový fyzikální obor – termodynamika. Termodynamika popisuje chování těles a látek z hlediska energie a tepla bez ohledu na jejich vnitřní strukturu. Jak uvidíme dále, jde o docela abstraktní teorii, jejíž platnost se neomezuje jen na tepelné stroje.

Zdroj
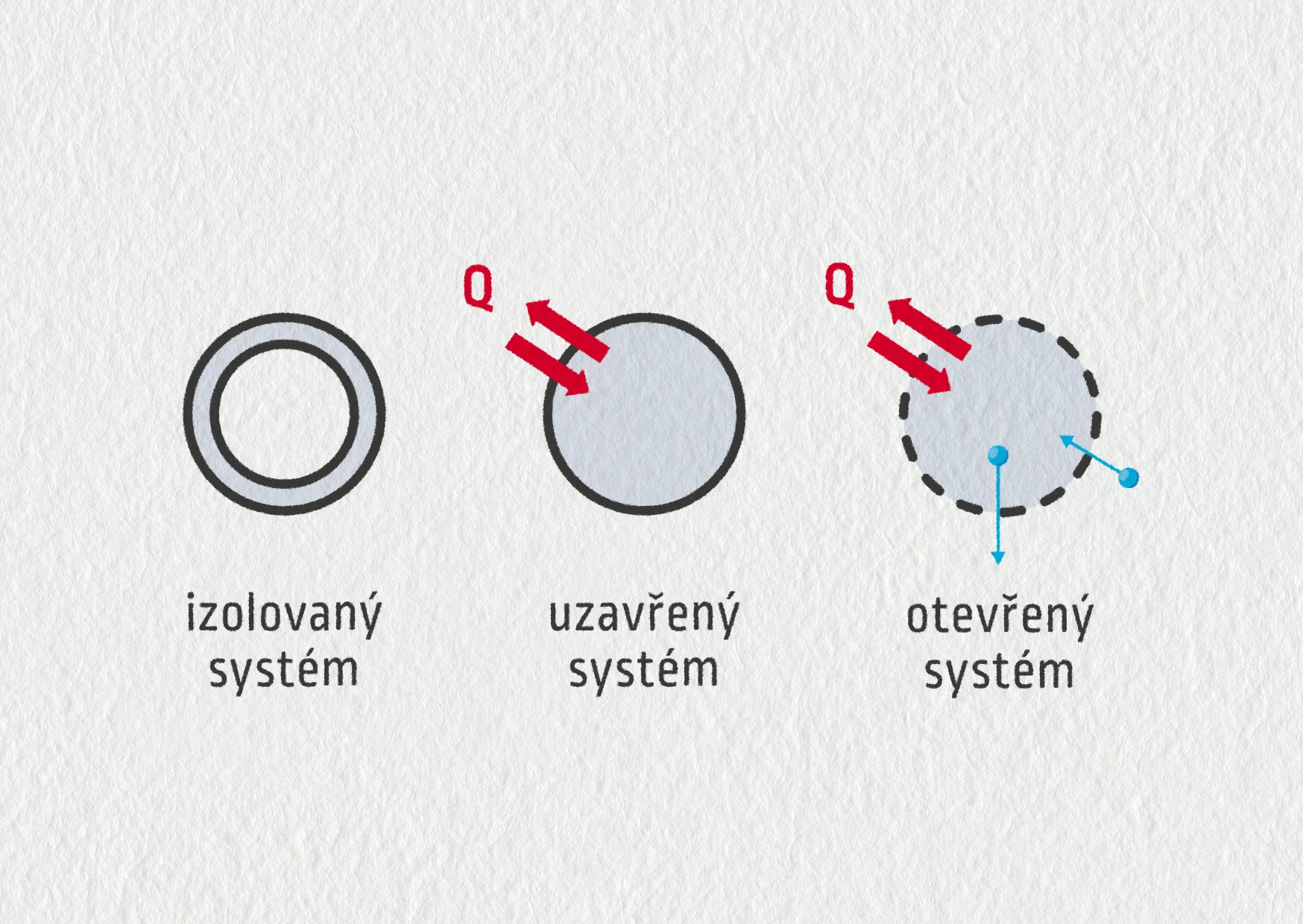
V předchozích kapitolách jsme zkoumali látky a děje v nich probíhající na úrovni molekul. Termodynamika však popisuje chování látek makroskopicky, aniž se zajímá o jejich vnitřní strukturu. Ústředním pojmem je zde termodynamický systém. Systém může být izolovaný, uzavřený nebo otevřený (viz obrázek). Představte si jej tak, že si ve vesmíru zvolíte přesně vymezenou oblast a budete zkoumat její interakci s okolím. Termodynamickým systémem může být parní stroj, člověk, plyn v nádobě nebo celá planeta. V dalším výkladu si představíme dva základní zákony, které popisují chování termodynamických systémů.
Zdroj
Doplňte a zdůvodněte, o jaký druh termodynamického systému se jedná:
- člověk
- Sluneční soustava
- čaj uzavřený v termosce
- člověk – otevřený systém, vyměnuje si s okolím energii i látku
- Sluneční soustava – uzavřený, systém odevzdává do okolí energii ve formě záření
- čaj uzavřený v termosce – izolovaný, ovšem jen pokud zanedbáme tepelné ztráty termosky.
První zákon termodynamiky
První zákon termodynamiky představuje zákon zachování energie. Chceme-li zvýšit vnitřní energii systému, nejde to jinak než dodáním energie z okolí. A naopak: pokud vnitřní energie systému klesá, systém do okolí energii odevzdává. Připomeňme, že vnitřní energie \(U\) je součtem kinetické a potenciální energie všech částic v systému (podrobněji v 10. kapitole). Zákon dále upřesňuje, že předávání energie mezi systémem a jeho okolím je možné pouze dvěma způsoby: pomocí mechanické práce \(W\) nebo tepla \(Q\). To je možné zapsat jednoduchou rovnicí:
První zákon termodynamiky
\[ \Delta U = W + Q \]Změna vnitřní energie systému je rovna součtu práce vykonané okolím a předaného tepla.
Znaménka v rovnici vyplývají z logiky zákona zachování energie. Pokud systém koná práci na okolních tělesech (a tím jim předává energii), nebo odevzdává teplo, mají \(W\) a \(Q\) záporná znaménka – vnitřní energie klesá. Pokud systém přijímá teplo, nebo koná práci okolí, mají \(W\) a \(Q\) kladná znaménka – vnitřní energie roste.
První termodynamický zákon popisuje pouze změny vnitřní energie. Pokud ve zvoleném systému probíhají také změny mechanické energie, pak celková energie systému je rovna součtu mechanické a vnitřní energie.
Celková energie systému je rovna součtu mechanické energie \(E_\mathrm{M}\) a vnitřní energie.
Pro izolovaný systém platí zákon zachování celkové energie \(E = E_\mathrm{M} + U = \hbox{konst.}\)
Nyní přejdeme ke konkrétním příkladům použití prvního termodynamického zákona.
-
Čaj chladne
Hrnek s horkým čajem stojí na stole a pomalu chladne. Systém hrnek + čaj předává svému okolí teplo, platí \(\Delta U=Q\), kde \(Q\) je záporné. Pokles vnitřní energie systému se projevuje snižováním jeho teploty.
-
Vzduch v pístu je prudce stlačen
Při prudkém stlačování koná píst (okolí) práci a zvyšuje vnitřní energii systému, platí \(\Delta U=W\). Zvýšení vnitřní energie se projeví zvýšením teploty vzduchu v pístu. Pokud by byl píst stlačován pomalu, docházelo by k předávání tepla do okolí již v průběhu stlačování a nárůst teploty plynu by nebyl tak velký. Děj, při kterém nedochází k předávání tepla mezi systémem a jeho okolím, se nazývá adiabatický. Při prudkém stlačení vzduchu se teplo nestihne předat, proto děj můžeme považovat za adiabatický.
-
Plyn z bombičky se prudce rozpíná
Pokud prorazíme sifonovou bombičku, unikající plyn se prudce rozpíná a odtlačuje okolní vzduch. Tím mu prací předává energii, a bombička se silně ochladí (viz obrázek). Tato situace je podobná stlačování pístu s tím rozdílem, že tentokrát koná práci systém (plyn v bombičce) a jeho vnitřní energie klesá, platí \(\Delta U=W\), kde \(W\) je záporné.

12.10b – Po expanzi vzduchu dojde k prudkému ochlazení bombičky
Zdroj -
Auto brzdí
Uvažujme systém auto + silnice. Auto brzdí díky třecí síle působící na brzdové kotouče, které se zahřívají. Zachovává se celková energie systému \(E=E_\mathrm{M}+U\). Díky působení třecí síly klesá mechanická energie a roste vnitřní energie. Platí \(\Delta U=\Delta E_\mathrm{M} = \frac12 mv^2\). Jinými slovy můžeme říci, že mechanická energie se při brzdění přeměnila na vnitřní energii. Elektrická auta dokáží mechanickou práci při brzdění využít k nabíjení baterie. Tím se rovněž zvyšuje vnitřní energie systému (automobilu), ale tentokrát jde o vnitřní potenciální energii.

12.11 – Při prudkém a dlouhém brzdění se brzdy extrémně zahřívají a hrozí jejich poškození.
Zdroj -
Člověk pracuje
Termodynamickým systémem může být i člověk. Představme si člověka třeba při chůzi. Svaly konají mechanickou práci, tělo produkuje odpadní teplo, platí \(\Delta U = W+Q\) (\(W\) i \(Q\) jsou záporné). Vnitřní energie systému klesá. V tomto případě jde o potenciální energii chemických vazeb – člověk spaluje cukry a tuky. Z vlastní zkušenosti dobře víme, že odpadního tepla při fyzické námaze se člověk potřebuje zbavit bez ohledu na okolní teplotu. Zatímco v zimě nás teplo příjemně zahřeje, v létě se ho zbavujeme silným pocením.
Zvlášť důležitými příklady termodynamických systémů jsou tepelné stroje a čerpadla, kterým se budeme věnovat podrobněji v další části. Nyní ještě vyřešíme několik zajímavých příkladů.
Cyklista při tréninku šlapal po dobu jedné hodiny s mechanickým výkonem 200 W. „Spálil“ přitom energii 3 600 kJ.
- Jaké teplo předal cyklista během tréninku svému okolí?
- Jaká je účinnost svalové práce cyklisty?
- Nejdřív vypočítáme vykonanou práci: \(W = Pt = 200\ \mathrm{W} ⋅ 3\,600\ \mathrm{s}=720\,000\ \mathrm{J}\). Pro výpočet tepla použijeme první zákon termodynamiky. Vnitřní energie cyklisty klesla o 3 600 kJ a vykonal práci 720 kJ. Zbytek energie tvoří odevzdané teplo: \(Q=3\,600\ \mathrm{kJ}-720\ \mathrm{kJ}=2\,880\ \mathrm{kJ}\).
- Účinnost svalové práce je \[ \eta = \frac{W}{\Delta U} = \frac{720\ \mathrm{kJ}}{3600\ \mathrm{kJ}} = 0{,}2 = 20\,\%\;. \]
Typické dělo ze 17. století (viz obrázek) dokázalo vystřelit železnou kouli o hmotnosti 8 kg rychlostí 500 m/s.
- Vypočítejte nárůst vnitřní energie soustavy koule + zeď při nárazu do zdi.
- Vypočítejte, o kolik by se ohřála dělová koule při nárazu za předpokladu, že by polovina vnitřní energie zůstala v kouli a polovina ve zdi.

Zdroj
Veškerá mechanická energie letící koule se při nárazu přemění na vnitřní. Změna vnitřní energie je proto
\[ \Delta U = E_\mathrm{K} = \frac12 mv^2 = \frac12 \cdot 8 \cdot 500^2\ \mathrm{J} = 10^6\ \mathrm{J} = 1\ \mathrm{MJ} \]Polovina vnitřní energie se využije k ohřevu koule: \(\frac12\Delta U = Q\).
Do rovnice dosadíme \(\frac14 mv^2 = mc\Delta T\) a vyjádříme neznámou \(\Delta T = v^2/4c\).
Číselně \(\Delta T = 500^2/(4\cdot450) = 140\ ^\circ\mathrm{C}\).
Druhý zákon termodynamiky
Představme si opět hrnek s čajem, který chladne na stole. Vnitřní energie z čaje je postupně předávána do okolního vzduchu, až nakonec čaj zcela vychladne a teploty se vyrovnají. Popsaný děj nemůže probíhat obráceně: vychladlý čaj se samovolně neohřeje od okolního vzduchu. Takové děje, které nemohou probíhat v čase samovolně obráceně, označujeme jako nevratné. Podívejme se ještě na jeden příklad: brzdění auta. Auto zpomaluje, klesá jeho mechanická energie a roste energie vnitřní – brzdy se zahřívají. Naopak to nejde. Není možné, aby horké brzdy automobil uvedly do pohybu, a tím se ochladily. Jinak je tomu ale v případě elektromobilu, který při brzdění nabíjí akumulátor. Nabitý akumulátor může auto opět rozpohybovat, děj může probíhat i obráceně. Nabíjení akumulátoru tedy můžeme označit jako děj vratný (i když u skutečného akumulátoru nedostaneme zpět přesně 100 % vložené energie).
Většina dějů kolem nás je nevratných a přijde nám to přirozené. Představte si třeba knihu, která vám spadla na zem. Pokud by kniha samovolně vyskočila ze země zpět do vaší ruky, asi byste byli dost zaskočeni. Přesto žádný z nevratných dějů neporušuje první termodynamický zákon, neboť celková energie se vždy zachovává. Kniha by při výskoku ze země získala mechanickou energii na úkor vnitřní energie. Přesně obráceně, než tomu bylo při jejím pádu.
K rozlišení dějů vratných a nevratných a k jejich popisu se ve fyzice používá veličina zvaná entropie. Entropie se definuje jako míra neurčitosti systému. Není to přesná definice, která by nám umožnila entropii vypočítat. Ale pokusíme se alespoň názorně přiblížit její význam, a to pomocí jednoduchého systému molekul v krabici.
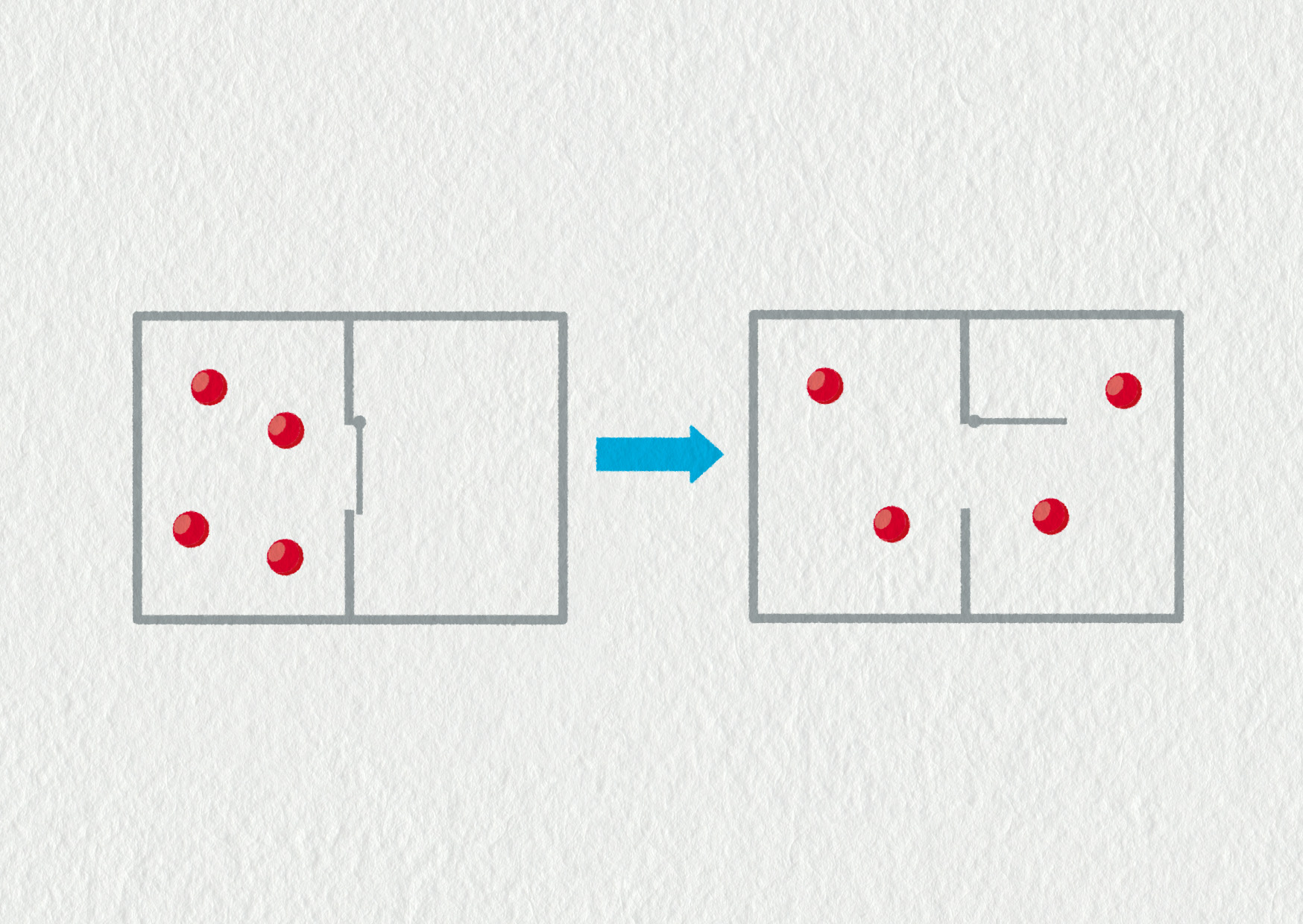
Představme si systém \(N\) molekul v krabici s přepážkou uprostřed. Po otevření přepážky budeme pozorovat nevratný děj: tlak plynu v obou částech krabice se postupně vyrovná. Stejný tlak odpovídá stejnému počtu molekul v obou částech krabice.
Zdroj
Všechny stavy, které mohou v tomto systému nastat, zapíšeme do přehledné tabulky. Molekuly si pracovně označíme písmeny a, b, c, d. Jako makrostav označujeme výslednou podobu dané konfigurace (kolik molekul je ve které polovině). Mikrostav je pak konkrétní realizace daného makrostavu pomocí určitých molekul. Důležité je, že všechny mikrostavy mají stejnou pravděpodobnost realizace (to platí až poté, co byla přepážka určitou dobu otevřena, a molekuly se mohly volně pohybovat krabicí).
| makrostav: (levá, pravá) | mikrostavy | počet mikrostavů | pravděpodobnost makrostavu |
|---|---|---|---|
| (4,0) | (abcd,–) | 1 | 1/16 = 0,0625 |
| (3,1) | (abc, d) (abd, c) (acd, b) (bcd, a) |
4 | 4/16 = 0,25 |
| (2,2) | (ab, cd) (ac, bd) (ad, bc) (bc, ad) (bd, ac) (cd, ab) |
6 | 6/16 = 0,375 |
| (1,3) | (a, bcd) (b, acd) (c, abd) (d, abc) |
4 | 4/16 = 0,25 |
| (0,4) | (–, abcd) | 1 | 1/16 = 0,0625 |
V tabulce vidíme, že různé makrostavy mají různé počty mikrostavů, kterými je můžeme realizovat. Stav (2,2) má největší pravděpodobnost realizace. Jinými slovy má největší neurčitost, neboť existuje 6 způsobů, jak ho vytvořit. Teď konečně dokážeme přesně zdůvodnit, proč je vyrovnání tlaků po otevření přepážky nevratným dějem. Stav (2,2) má šestkrát větší počet možností realizace než stav (4,0). Jsou to náhodné procesy (v tomto případě srážky molekul), které zajistí, že systém směřuje do stavu s největší pravděpodobností realizace (největší neurčitostí). Proto je entropie definována jako míra neurčitosti systému. Při náhodných procesech se entropie zvyšuje, a podle toho můžeme poznat nevratné děje.
Nyní můžeme pokročit k formulaci druhého zákona termodynamiky pomocí entropie.
Druhý zákon termodynamiky
\[ \Delta S \ge 0 \]Entropie uzavřeného systému nikdy neklesá. Při nevratném ději entropie roste \( ( \Delta S > 0 ) \) a při ději vratném zůstává stejná \( ( \Delta S = 0 ) \).
Mějme krabici s přepážkou a v ní 6 stejných molekul.
- Popište stav, který má největší entropii.
- Vypočítejte počet mikrostavů pro stav s největší entropií.
- Vypočítejte pravděpodobnost, že se systém dostane do stavu, kdy všechny molekuly budou vpravo a žádná vlevo. Nápověda: Celkový počet všech možných mikrostavů můžeme určit snadno jako 26 (každá molekula má právě dvě možnosti, kde se bude nacházet).
- Je to stav (3,3), tedy 3 molekuly vpravo a 3 vlevo.
- Nemusíte všechny mikrostavy pro stav (3,3) vypisovat, pokud znáte kombinační čísla. Počet způsobu, jak vybrat 3 molekuly z 6, je \(\displaystyle {6\choose 3} = 20\). Pokud neznáte kombinační čísla, zkuste možnosti spočítat „ručně“.
- Stav (0,6) má jedinou možnost realizace, proto \(p = 1/2^6 = 1/64 = 0{,}0015625\).
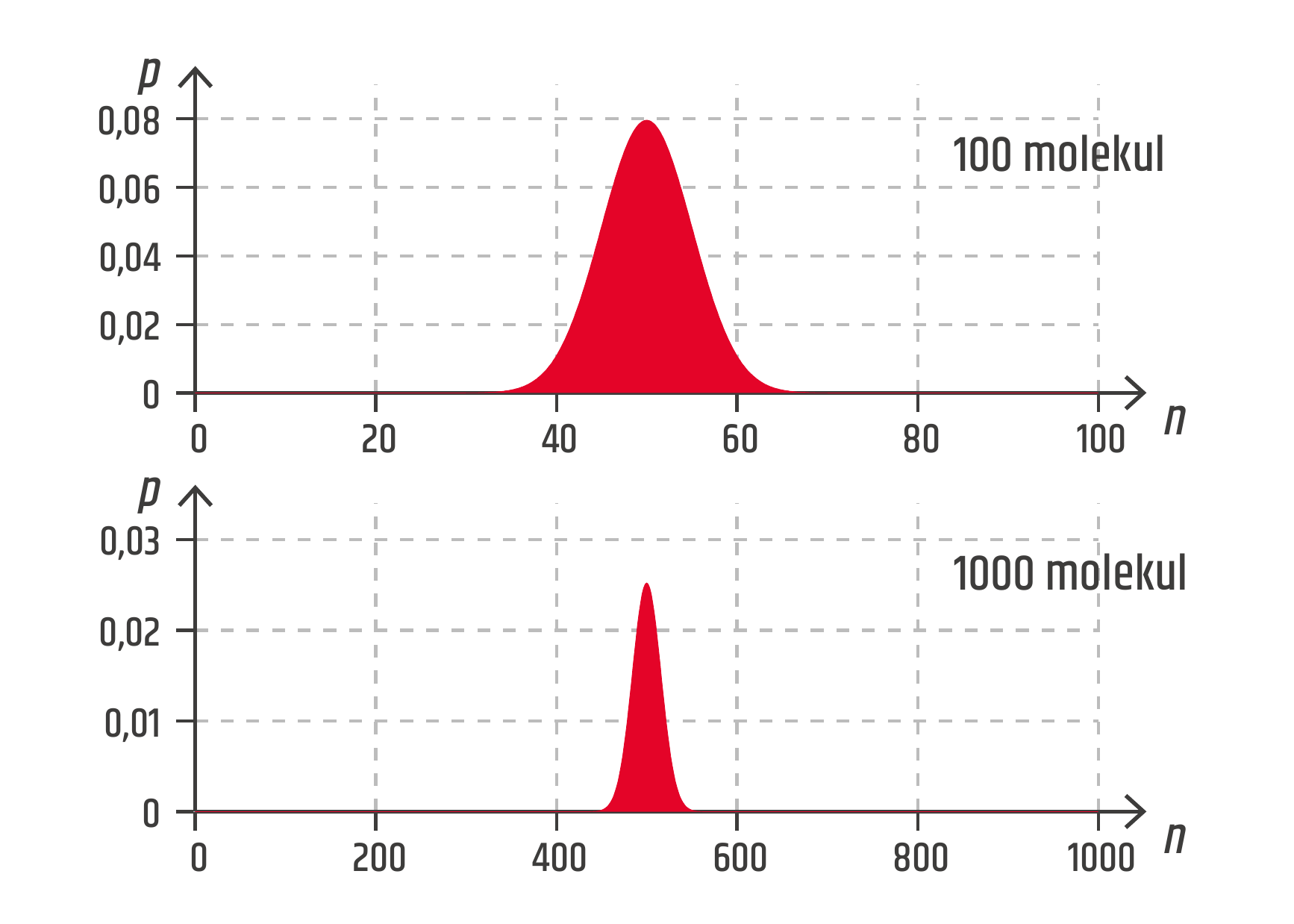
Na příkladu s molekulami v krabici je vidět, že pravděpodobnost stavů s nižší entropií je menší, ale není nulová. Z toho vyplývá, že i tyto stavy se mohou vyskytovat. Budeme-li krabici chvíli pozorovat, občas se dočkáme situace, kdy entropie samovolně klesne a molekuly se nahromadí v jedné části. Tohle se bude stávat při malém počtu molekul v krabici. Vzpomeňte si, jak malé jsou atomy a molekuly! V jednom molu látky se jich nachází řádově 1023. Pro velké počty molekul se pravděpodobnostní rozložení zužuje, a výrazně nerovnoměrná rozdělení molekul se stávají méně pravděpodobnými (viz graf).
Zdroj
Pravděpodobnost náhodného výskytu výrazně nevyrovnaných stavů pro 1 mol látky v krabici je tak malá, že si to ani neumíme představit. Uvažte, že všech možných mikrostavů je \(\displaystyle 2^{10^{23}}\). Toto číslo je tak velké, že kdybychom ho chtěli zapsat na jeden řádek, jeho délka by byla řádově 1019 m, to je 1 000 světelných let! Systém mnoha molekul se proto bude neustále nacházet ve stavech blízkých maximální entropii, kdy je počet molekul přibližně stejný na obou stranách. Jde o velmi zvláštní fyzikální zákon. Jeho platnost není absolutní. Děje, při kterých se entropie samovolně snižuje, nejsou zcela zakázané, ale jen velmi nepravděpodobné. Díky obrovskému počtu molekul v běžných systémech se na něj přesto můžeme spolehnout. Nemusíme se obávat, že se vzduch v místnosti nečekaně shromáždí jen v jedné její části nebo že se nám voda ve sklenici z ničeho nic samovolně ohřeje od okolního vzduchu.

Zdroj
Druhý termodynamický zákon, někdy též nazývaný zákon růstu entropie, patří mezi nejdůležitější fyzikální zákony. Určuje, které děje mohou probíhat samovolně a které nikoliv. My se zde nebudeme pouštět do výpočtu entropie ve složitějších systémech. Pro náš odhad, zda entropie roste či klesá, nám dobře poslouží jednoduché pravidlo. Největší neurčitost je spojena s tepelným (chaotickým) pohybem atomů a molekul. Proto se entropie zvyšuje při dějích, kdy se jiné formy energie mění na vnitřní kinetickou energii (tělesa se ohřívají). Někdy se také říká, že zákon určuje směr plynutí času. Budeme-li za uzavřený systém považovat celý vesmír, pak je jasné, že jeho entropie neustále roste, neboť v něm probíhá řada nevratných dějů. V systému, který není uzavřený, můžeme entropii snížit, ale bude to vždy za cenu zvýšení entropie v jeho okolí. Přesně tak to dělají tepelné stroje, které mění teplo na mechanickou práci. Právě jejich principu se budeme věnovat v další části této kapitoly.

