Polarizace
Cvičení 1
Uvažujme uspořádání dvou experimentů s polarizačními filtry dle následujícího obrázku.
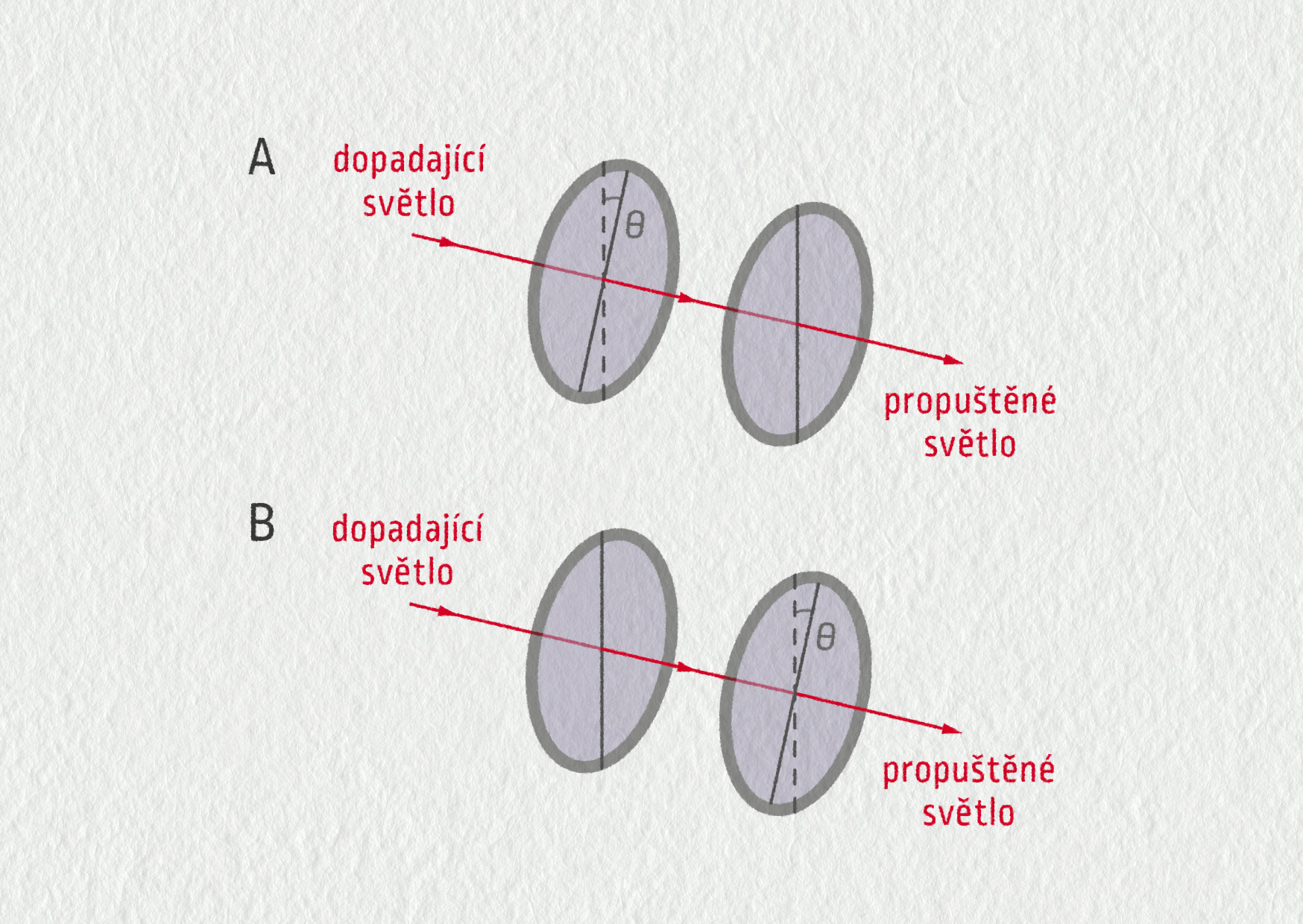
Zdroj
Za předpokladu, že dopadající světlo není polarizované, určete, zda je intenzita propuštěného světla větší v uspořádání A, menší v uspořádání A, nebo je v obou uspořádáních A i B stejná. Odpověď zdůvodněte.
Cvičení 2
Uvažujme uspořádání dvou experimentů s polarizačními filtry dle předchozího obrázku.
Dopadající světlo je vodorovně polarizované. Vyberte správné tvrzení o intenzitě propuštěného světla:
- Intenzita propuštěného světla je v obou případech stejná, protože úhel otočení polarizační roviny \( \theta \) mezi filtry je v obou případech stejně velký.
- Intenzita propuštěného světla je větší v případě B, protože všechno světlo prochází přes první polarizační filtr.
- Intenzita propuštěného světla je menší v případě B než v případě A. Světlo propuštěné v případě B má dokonce nulovou intenzitu, protože první polarizační filtr je orientován svisle.
Cvičení 3
Jak by měla být orientována polarizační rovina brýlí, které by zamezily odleskům na skleněné ploše na následujícím obrázku? Odpověď vysvětlete.

Zdroj
Cvičení 4
Opticky aktivní látky jsou takové, které stáčí rovinu polarizace světla. Úhel, o který je při průchodu takovou látkou otočena rovina polarizovaného světla, závisí na koncentraci látky v roztoku.
V průběhu expriementu byly pomocí polarimetru měřeny hodnoty intenzity světla, které prošlo dvěma polarizačními filtry a cukerným roztokem, vloženým do prostoru mezi nimi.
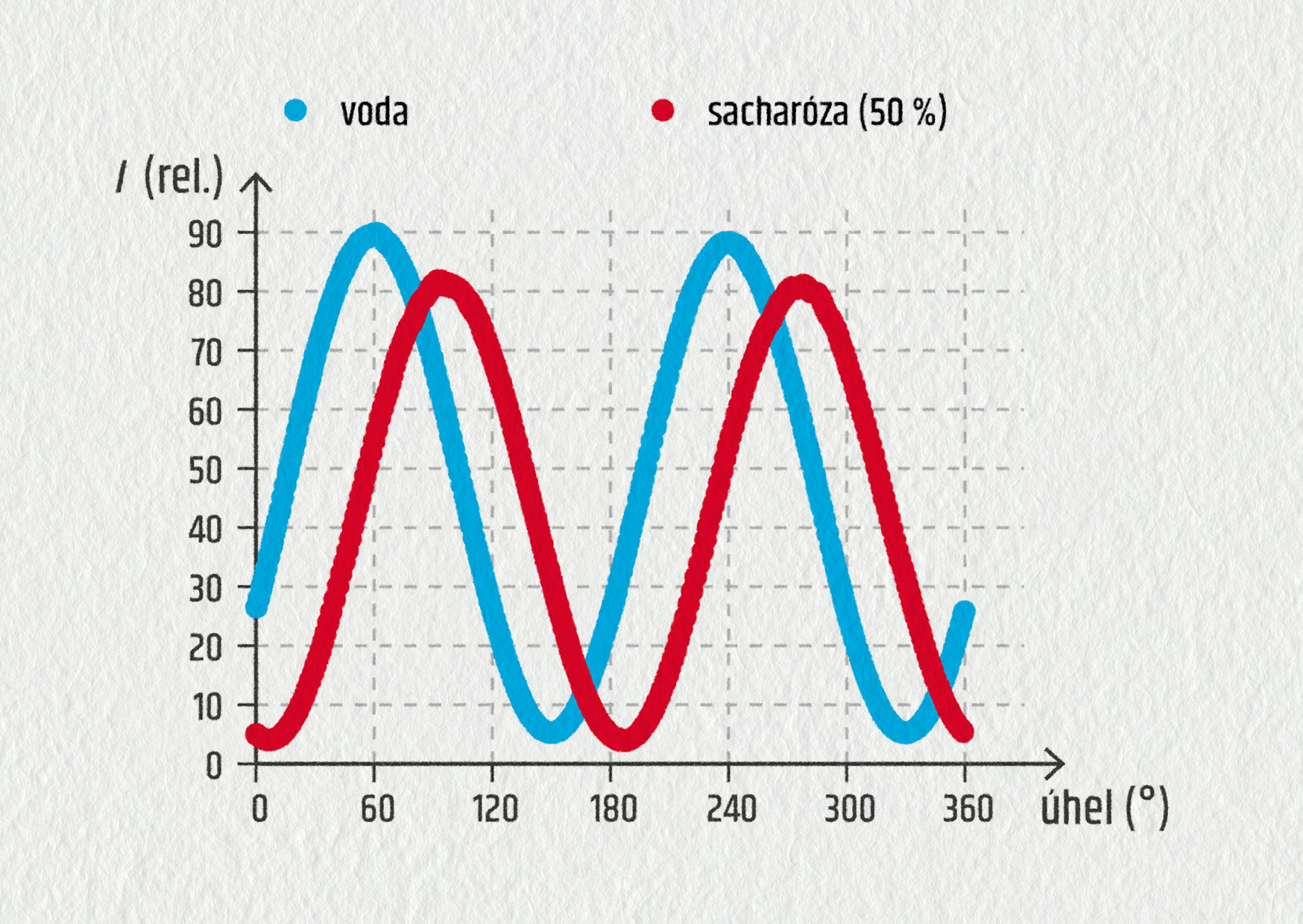
Zdroj
Při opakovaném měření pro roztoky různých koncentrací byly naměřeny tyto hodnoty:
| látka | koncentrace \(c\) (% původního roztoku) | úhel pootočení roviny polarizace \(\theta\) (°) |
|---|---|---|
| destilovaná voda | 0 | 0 |
| sacharóza | 100 | 73,5 |
| sacharóza | 50 | 35,5 |
| sacharóza | 25 | 18 |
| sacharóza | 12,5 | 8,2 |
| sacharóza, neznámá koncentrace | ? | 18,7 |
- Sestrojte graf závislosti úhlu pootočení roviny polarizace \(\theta\) na koncentraci roztoku \(c\).
- Určete, o jaký druh závislosti se jedná. Najděte jeho matematický model.
- Ze získané rovnice určete neznámou koncentraci sacharózy v posledním měření.
- a) Viz obrázek 24.62 níže;
- Jde o přímou úměrnost. Rovnice matematického modelu hledané závislosti je \(\theta=0{,}73c\);
- \(c=25{,}6\ \%\).
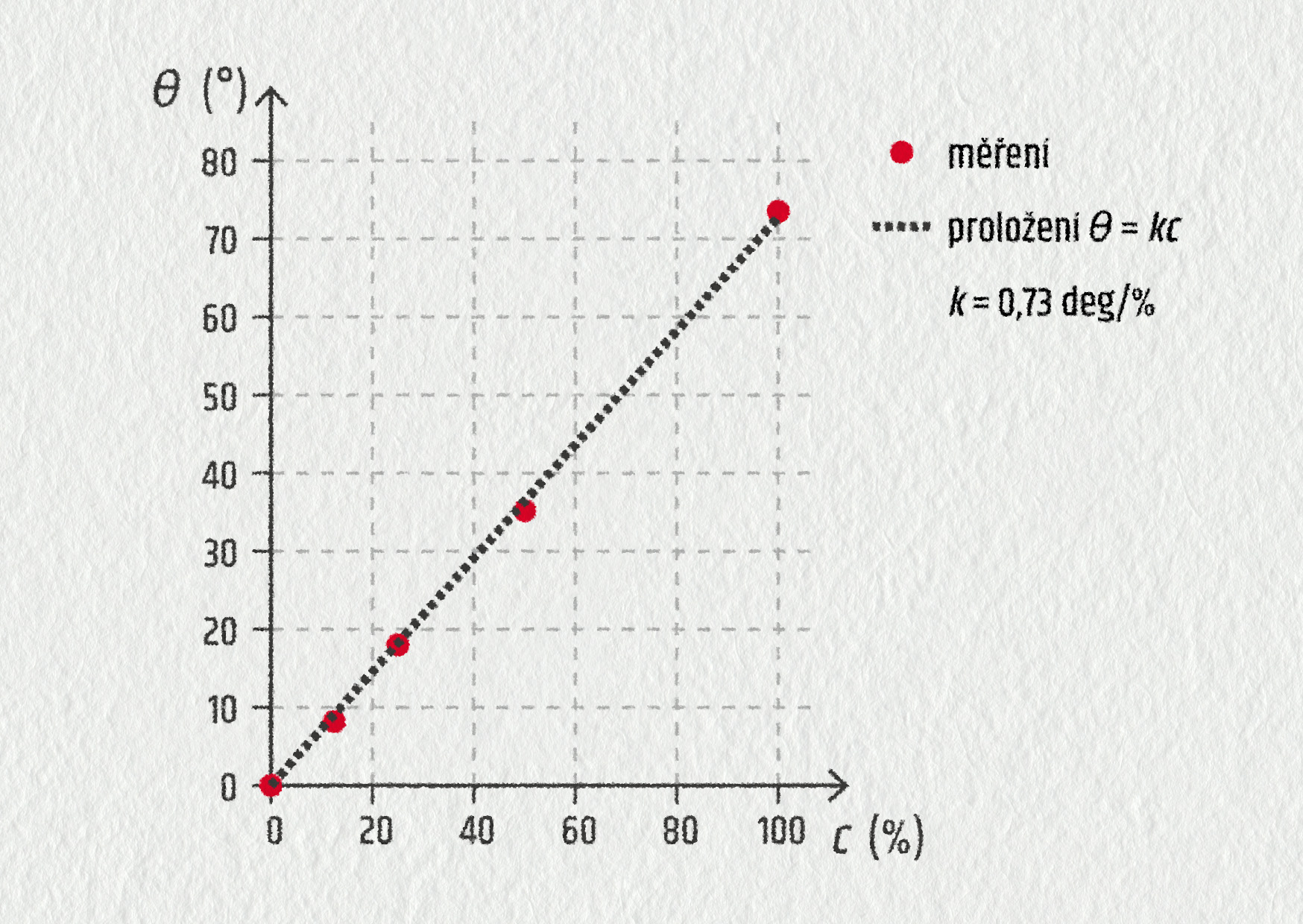
Zdroj

