Radioaktivita
Cvičení 1
S využitím periodické tabulky prvků doplňte zápis jaderných reakcí.
\[\begin{aligned} {}^{234}_{\hphantom{0}92}\mathrm{U} &\to \dots + {}^4_2\mathrm{He}\\ \dots &\to {}^{36}_{18}\dots + {}^{\hphantom{-}0}_{-1}\mathrm{e} + \dots\\ {}^{\dots}_{16}\mathrm{S} &\to {}^{30}_{\dots}\dots + {}^0_1\mathrm{e} + \dots\\ \dots &\to {}^{206}_{\hphantom{0}82}\mathrm{Pb} + \gamma\\ \end{aligned}\]Cvičení 2
Proč je zemská kůra radioaktivní.
Oblasti zemské kůry, které obsahují uran, vykazují zvýšenou radioaktivitu. Samotný uran je α zářič a přeměňuje se na thorium, které je rovněž radioaktivní, a produkty jeho přeměny jsou opět radioaktivní. V podloží tak vzniká celá řada radioaktivních látek, které přispívají k jeho aktivitě. Tato rozpadová řada končí stabilním olovem. S pomocí následujícího schématu uran-radiové řady a periodické tabulky prvků zjistěte, jaké radioaktivní látky se v podloží vyskytují. Produkt určité přeměny je vždy reaktantem přeměny následující.
\[ {}^{238}_{\hphantom{0}92}\mathrm{Th} \stackrel{\alpha}{\longrightarrow} {}^{\dots}_{\dots}\mathrm{Th} \stackrel{\beta^-}{\longrightarrow} \dots \stackrel{\beta^-}{\longrightarrow} \dots \stackrel{\alpha-}{\longrightarrow} \dots \stackrel{\alpha-}{\longrightarrow} \dots \stackrel{\alpha-}{\longrightarrow} \dots \stackrel{\alpha-}{\longrightarrow} \dots \stackrel{\alpha-}{\longrightarrow} \dots \stackrel{\beta^-}{\longrightarrow} \dots \stackrel{\beta^-}{\longrightarrow} \dots \stackrel{\alpha-}{\longrightarrow} \dots \stackrel{\beta^-}{\longrightarrow} \dots \stackrel{\beta^-}{\longrightarrow} \dots \stackrel{\alpha-}{\longrightarrow} {}^{206}_{\hphantom{0}82}\mathrm{Pb} \]
Zdroj
Cvičení 3
Polonium \(^{210}_{\hphantom{0}84}\mathrm{Po}\) je α zářič a přeměňuje se na olovo.
- Napište rovnici přeměny.
- Vypočítejte v MeV energii uvolněnou při přeměně jednoho jádra polonia.
Hmotnosti jednotlivých jader:
\[\begin{aligned} m_\mathrm{Po} &= 209{,}9367\ \mathrm{u}\\ m_\mathrm{Pb} &= 205{,}9295\ \mathrm{u}\\ m_\mathrm{He} &= 4{,}0015\ \mathrm{u}\\ \end{aligned}\]Cvičení 4
Tritium \({}^3_1\mathrm{H}\) je v přírodě velmi vzácný radioaktivní izotop vodíku. Lze jej vyrábět ozařováním kovového lithia a v malém množství vzniká záchytem neutronů ve vodíku při běžném provozu jaderných reaktorů. Tritium je zářič \(\beta ^ - \).
- Napište rovnici přeměny.
- Vypočítejte hmotnosti jader tritia a helia.
- Vypočítejte energii v keV uvolněnou při přeměně jednoho jádra tritia. Klidovou energii neutrin zanedbejte.
Zadané hodnoty:
- hmotnost atomu tritia \(m_\mathrm{T}=3{,}0140493\ \mathrm{u}\)
- hmotnost vzniklého atomu helia \(m_\mathrm{He}=3{,}0160293\ \mathrm{u}\)
- hmotnost elektronu \(m_\mathrm{e}=5{,}486\cdot10^{-4}\ \mathrm{u}\)
Cvičení 5
Poločas přeměny izotopu polonia \({}^{221}\mathrm{Po}\) je 25 s. Předpokládejme, že v čase \(t=0\ \mathrm{s}\) obsahuje vzorek 200 miliard jader \({}^{221}\mathrm{Po}\). Kolik radioaktivních jader polonia bude ve vzorku v čase
- t = 25 s,
- t = 50 s,
- t = 100 s,
- t = 500 s.
- 100 miliard;
- 50 miliard;
- 12,5 miliardy;
- (200 miliard)/220 ≈ 190 tisíc
Cvičení 6
Radon ve stavebnictví.
Radon je radioaktivní plyn vznikající postupným rozpadem uranu. Štěrbinami v podloží je komínovým efektem nasáván k povrchu země. Protože jde o těžké atomy (nejtěžší z inertních plynů, sedmkrát těžší než molekula O2), má tendenci se hromadit ve sklepních místnostech. V pobytových prostorech novostaveb nesmí aktivita radonu překročit 200 Bq/m3. Poločas rozpadu izotopu \({}^{222}\mathrm{Rn}\) je 3,82 dní. Vypočítejte:
- hmotnost v kg jednoho atomu radonu,
- konstantu radioaktivní přeměny,
- počet atomů radonu v 1 m3 odpovídající limitní hodnotě aktivity.
Další praktické informace najdete na stránkách Státního ústavu radiační ochrany.
- 3,69 ⋅ 10−25 kg;
- 2,10 ⋅ 10−6 s−1;
- 9,52 ⋅ 107
Cvičení 7
Jak dlouho bude aktivní vyhořelé jaderné palivo?
Vyhořelé palivo z jaderných elektráren obsahuje cesium \({}^{137}\mathrm{Cs}\) a stroncium \({}^{90}\mathrm{Sr}\) s poločasem přeměny 30,0 let. Vypočítejte:
- konstantu radioaktivní přeměny,
- aktivitu vzorku obsahujícího jeden gram čistého \({}^{137}\mathrm{Cs}\),
- o kolik procent se sníží aktivita tohto vzorku za 100 let,
- za jak dlouho poklesne aktivita tohoto vzorku na hodnotu 50 kBq, což je přirozená aktivita jednoho gramu uranu v podloží.
Kdy je vyhořelé palivo nejnebezpečnější? Bude vyhořelé palivo zářit ještě 10 000 let, jak občas slyšíme v médiích? Zkuste to spočítat. Argumentujte.

Zdroj
- 7,32 ⋅ 10−10 s−1;
- 3,22· 1012 Bq;
- o 90 %;
- za 780 let
Cvičení 8 – Radiouhlíková metoda
K určení stáří nalezeného dřevěného hudebního nástroje využili archeologové radiouhlíkovou metodu. Aktivita historického vzorku byla o 26,5 % nižší než aktivita stejně velkého vzorku dřeva ze současnosti. Poločas rozpadu uhlíku 14 je 5 730 let. Určete stáří nástroje. Mohl patřit slavnému Pythagorovi ze Samu?
Cvičení 9
Určování stáří Země
Stáří Země je přibližně 4,54 miliardy let s nepřesností jeho určení ±70 milionů let. Toto číslo je kompromisem mezi věkem nejstaršího minerálu nalezeného na Zemi – zirkonu z Jack Hills v Austrálii a astrofyziky odhadovaného věku sluneční soustavy.
Čistý zirkon (ZrSiO4 – křemičitan zirkoničitý) je minerál, který vzniká krystalizací při tuhnutí roztavené horniny, například žuly. Během procesu krystalizace mohou být některé atomy zirkonia nahrazeny uranem. Totéž se nedá říci o olovu – v době vzniku krystalu neobsahuje zirkon žádné olovo.

Zdroj
Uran je radioaktivní a přes řadu meziproduktů se přeměňuje na stabilní olovo. Poločas rozpadu samotného uranu 238 je 4,47 ⋅ 109 let, o mnoho řádů vyšší než poločas rozpadu ostatních meziproduktů. Proto čas potřebný k přeměně těchto meziproduktů zanedbáme.
Na hmotnostním spektrometru bylo zjištěno, že v australském zirkonu připadá na 51 jader uranu právě 50 jader olova. Vypočítejte stáří tohoto vzorku.
Cvičení 10
Elektrický náboj a někdy i hmotnost částic ionizujícího záření můžeme zjistit pomocí jejich pohybu v magnetickém poli. Předpokládejme, že na obrázku 27.37 je magnetické pole homogenní. Která křivka odpovídá
- α záření,
- β− záření,
- β+ záření,
- γ záření,
- proudu neutronů?
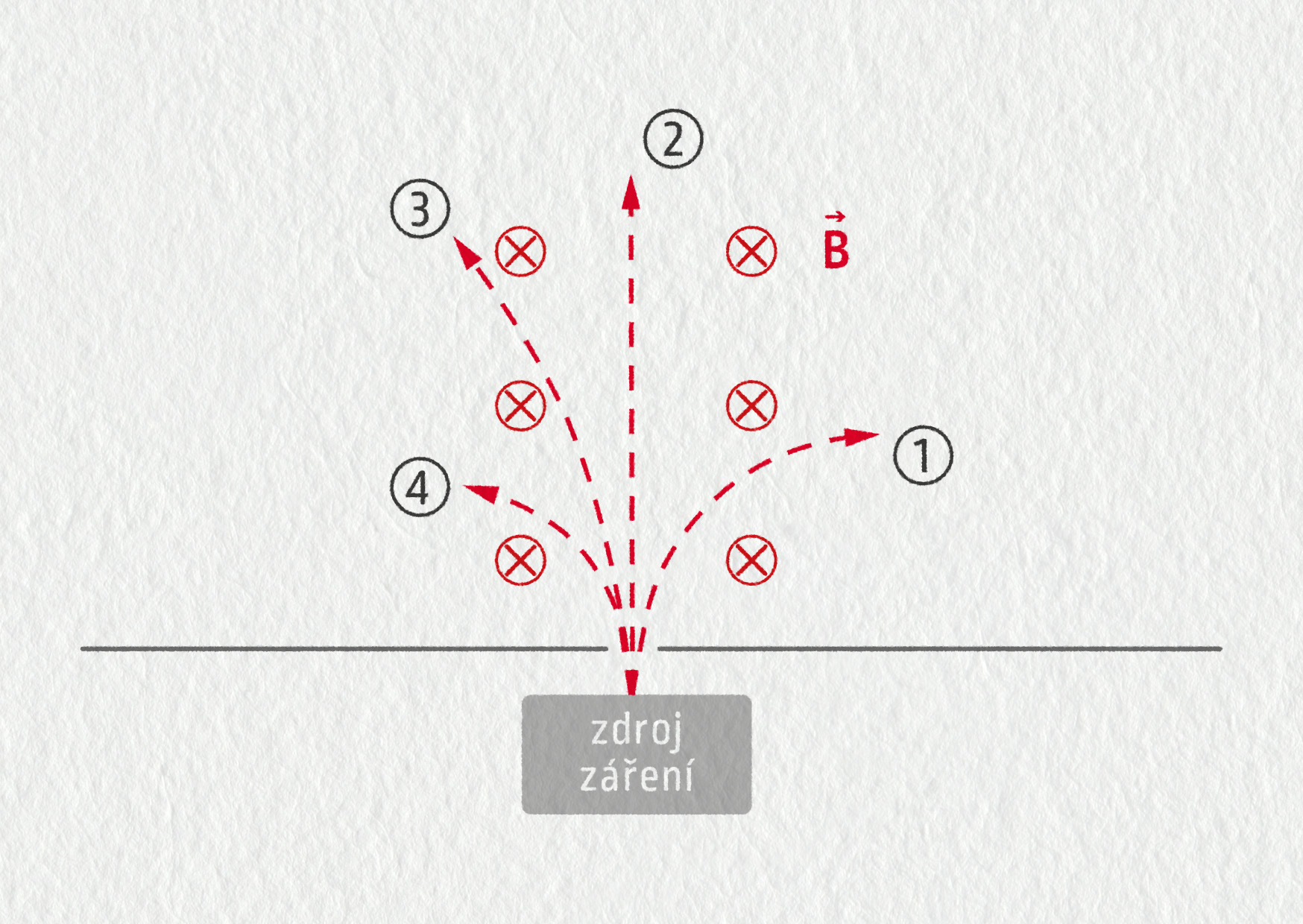
Zdroj
- 3;
- 1;
- 4;
- 2;
- 2; určování směru magnetické síly je vysvětleno v kapitole 19.

