Magnetická síla působící na nabitou částici
Magnetická síla a její zvláštní vlastnosti byly objevovány pomocí experimentů, kdy na sebe působí magnety a vodiče protékané proudem. Můžete si je sami vyzkoušet v motivační aktivitě. Tento výzkum nakonec umožnil konstrukci mnoha praktických zařízení, jako jsou elektromotory či generátory. S nimi se podrobněji seznámíme později.
Historii nyní přeskočíme a představíme si již „hotový“ základní fyzikální zákon pro magnetickou sílu. Magnetická síla působí pouze v případě, kdy se nabitá částice pohybuje v magnetickém poli.
Určit správně směr magnetické síly není tak snadné. Je to výzva pro vaši prostorovou představivost! Tak pojďme na to a sledujme vše na obrázku 19.23. Magnetická síla je vždy kolmá na vektor magnetické indukce \(\Vec{B}\) a také na vektor rychlosti částice \(\Vec{v}\). To ale nestačí, stále jsou tu dvě možnosti (v našem příkladu nahoru a dolů). K určení jednoho správného směru proto musíme použít pravidlo pravé ruky, které je naznačeno na obrázku 19.23 vpravo. Ani tak to ještě není všechno. Směr síly je ovlivněn také znaménkem pohybujícího se náboje. Pomocí pravé ruky určíme směr síly pro kladnou částici. Je-li náboj částice záporný, obrací se směr síly na opačný.
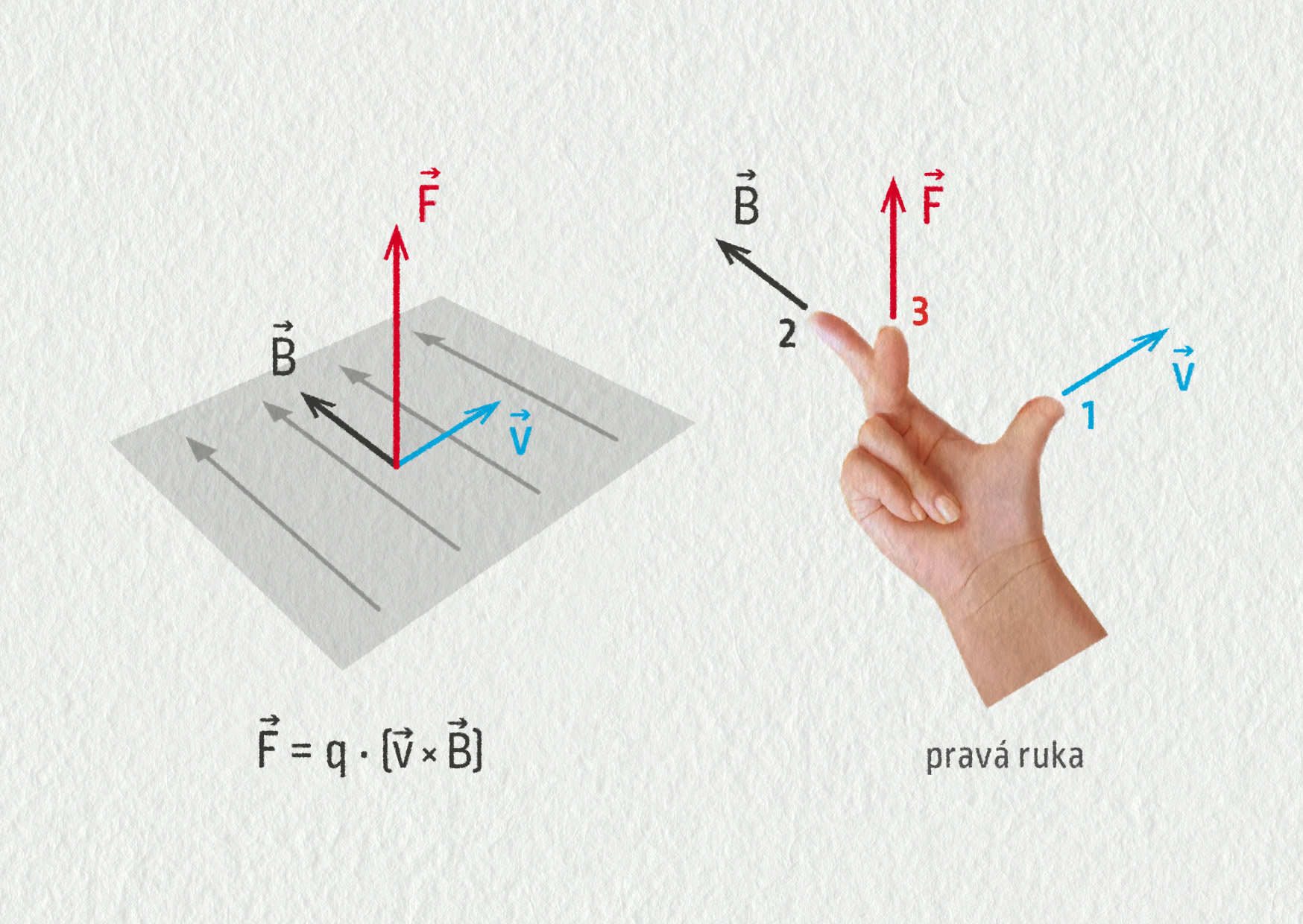
Zdroj
Pro velikost magnetické síly pak platí \(F=qvB\sin\alpha\), kde \(\alpha\) je úhel mezi vektory \(\Vec{v}\) a \(\Vec{B}\). Matematicky vše můžeme popsat velmi jednoduše pomocí vektorového součinu \(\Vec{v}\times\Vec{B}\). Před tento součin ještě napíšeme náboj \(q\), který pro záporné náboje obrací sílu opačným směrem.
Magnetická síla na nabitou částici:
\[ \Vec{F} = q\Vec{v}\times\Vec{B} \]Velikost síly: \(F=qvB\sin\alpha\), kde \(\alpha\) je úhel mezi vektory \(\Vec{v}\) a \(\Vec{B}\).
Směr síly: pomocí vektorového součinu (pravidlem pravé ruky) a znaménka náboje.
Možná si říkáte, že tohle je pustá teorie. Máte pravdu v tom, že doma v kuchyni běžně nevidíte létat nabité částice. To je proto, že v kuchyni máte vzduch. Abychom působení magnetické síly na pohybující se částice snadno zpozorovali, musíme je umístit do vakua. Možné uspořádání takového experimentu vidíte na ilustraci. Z katody (záporné elektrody) budou při dostatečně vysokém napětí vyletovat elektrony, které po průchodu malým otvorem vytvoří úzký svazek. Ten následně můžeme vychylovat magnetickým polem.
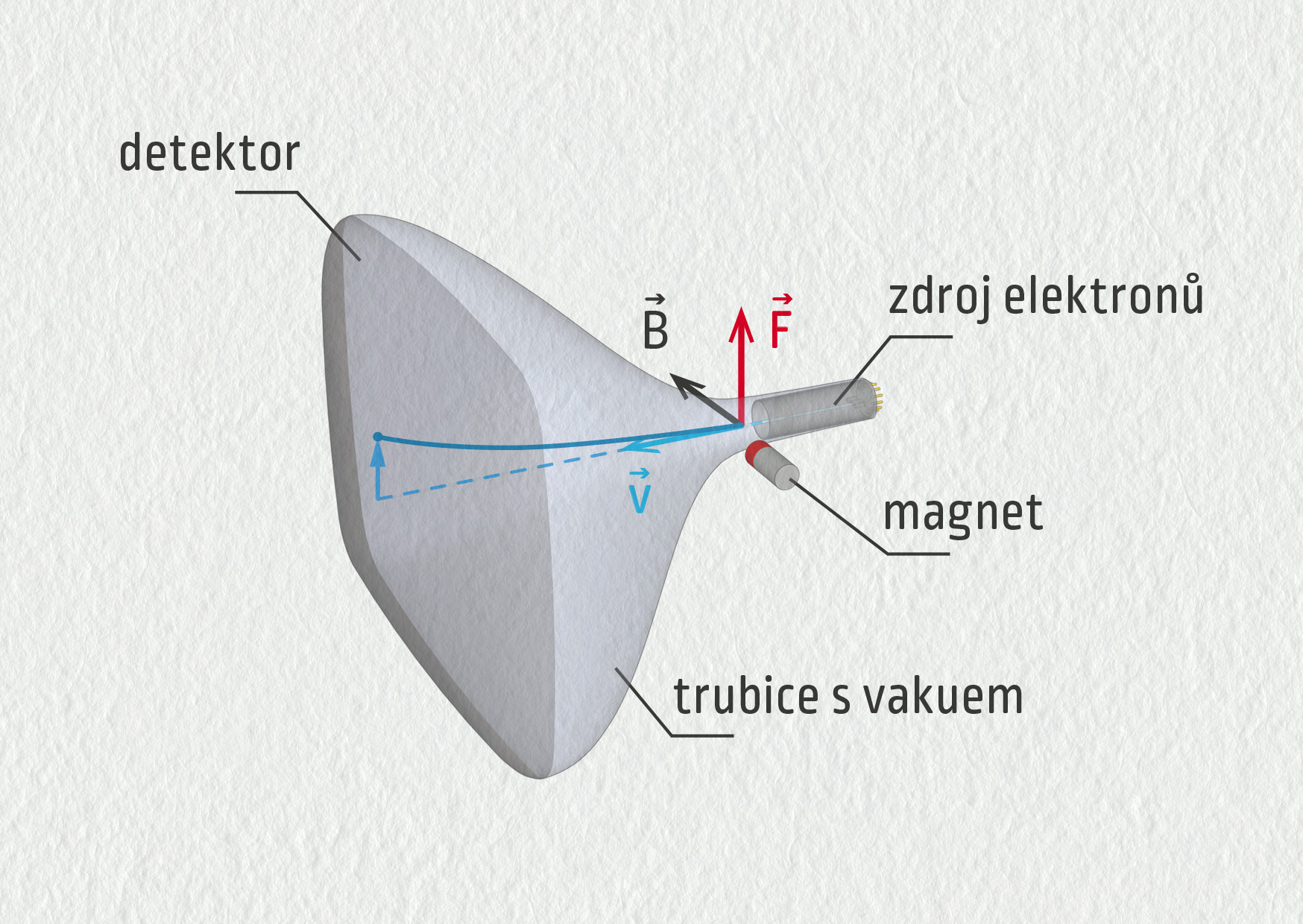
Zdroj
Ověřte, zda je směr magnetické síly v experimentu s elektrony správně určen (viz obrázek).
Použitím pravé ruky zjistíme, že vektorový součin směřuje dolů. Elektrony však mají záporný náboj, proto bude směr síly opačný – bude směřovat nahoru. To je v souladu s původním obrázkem.
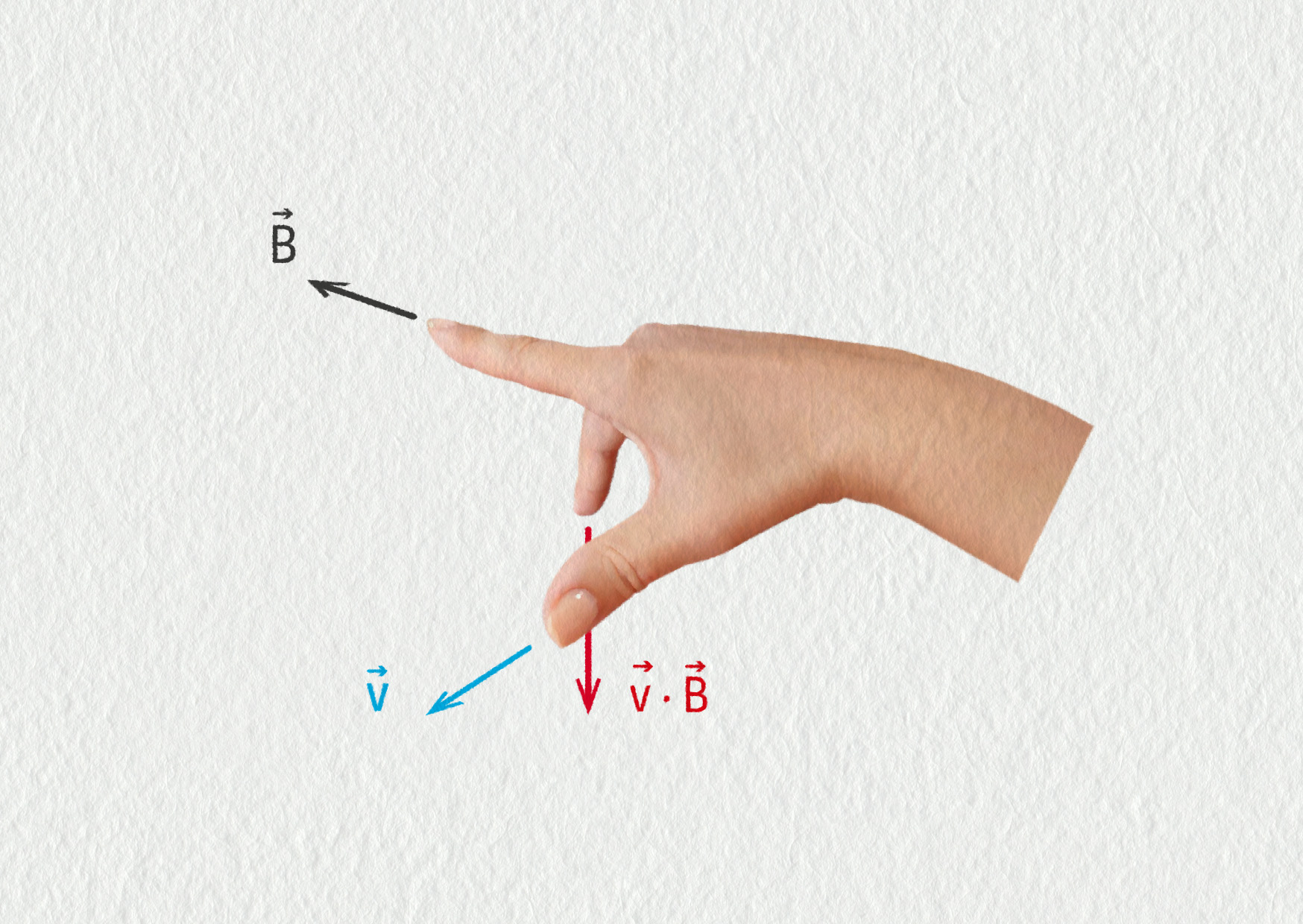
Zdroj
Analyzátor částic rozeznává jejich náboj a případně i hmotnost podle jejich pohybu v magnetickém poli. Přiřaďte k částicím jejich trajektorii podle obrázku (magnetické pole je přibližně homogenní).
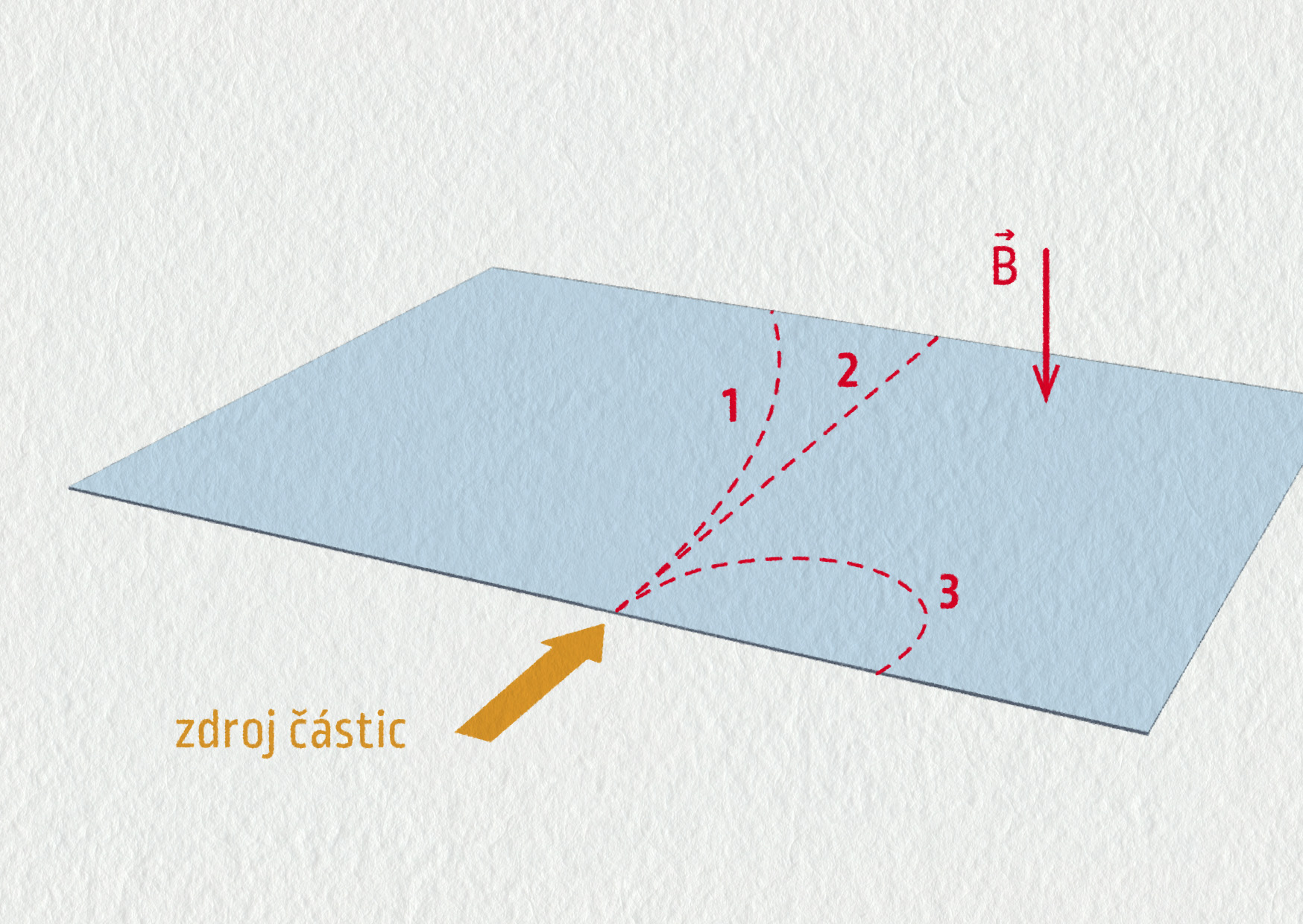
Zdroj
Ve druhé polovině 19. století studovali fyzikové tzv. katodové paprsky. Při experimentu byla používána výbojová trubice, což je skleněná trubice s elektrodami. Pokud byl plyn uvnitř trubice zředěn a na elektrody bylo připojeno vysoké napětí (desítky Voltů), začal plyn v trubici zářit. W. Crookes kolem roku 1880 zjistil, že při dalším snížení tlaku začíná kromě plynu uvnitř světélkovat i skleněná stěna baňky v místech, která leží naproti záporné elektrodě (katodě). Předpokládal tedy, že katoda emituje záření, které nazval katodové záření. Prováděl další experimenty, ze kterých vyplynulo, že záření přenáší energii (záření roztáčelo lopatky miniaturního „mlýnku“).
Podstatu katodového záření odhalil v roce 1897 J. J. Thomson, anglický experimentální fyzik a ředitel slavné Cavendishovy laboratoře na Univerzitě v Cambridge. Za svůj objev dostal v roce 1906 Nobelovu cenu za fyziku. Thomson na základě výše uvedených experimentů předpokládal, že katodové záření je tvořeno proudem malých částic se záporným nábojem. Thomson vychyloval proud katodového záření postupně elektrickým a magnetickým polem. Z rovnosti těchto dvou sil pak mohl určit rychlost částic. V kombinaci se vzorcem pro kinetickou energii dokázal určit poměr \(q/m\) pro částice katodového záření. Zjistil, že tento poměr je o tři řády větší než například u iontů. Proto správně usoudil, že se musí jednat o zvláštní, velmi lehké nabité částice, které se uvolňují z atomů. Teprve později byl určen jejich elektrický náboj a hmotnost.

Zdroj
Vletí-li nabitá částice do homogenního magnetického pole, jsou celkem tři možnosti, jak se může pohybovat. Záleží na tom, jaký je směr rychlosti částice vzhledem k vektoru \(\Vec{B}\). Na obrázku vidíme, že nejjednodušší situace nastane v případě, kdy je směr vektorů \(\Vec{v}\) a \(\Vec{B}\) shodný (nebo opačný). V tomto případě magnetická síla na částici nepůsobí a ta se pohybuje rovnoměrně přímočaře. Vletí-li částice do magnetického pole kolmo na \(\Vec{B}\), bude se díky magnetické síle pohybovat rovnoměrně po kružnici. Je to proto, že magnetická síla bude neustále kolmá na rychlost a bude tak tvořit dostředivou sílu. Jak to dopadne v případě, kdy částice vletí do magnetického pole šikmo? Rychlost částice v můžeme rozložit do dvou kolmých směrů, jak ukazuje obrázek. Rychlost \(v_z\) ve směru \(\Vec{B}\) se nebude měnit. Rychlost \(v_x\) je naopak kolmá na \(\Vec{B}\). Proto bude výsledný pohyb složením kruhového pohybu v rovině xy a rovnoměrného pohybu ve směru osy z. Částice se bude pohybovat po šroubovici podél magnetických indukčních čar.
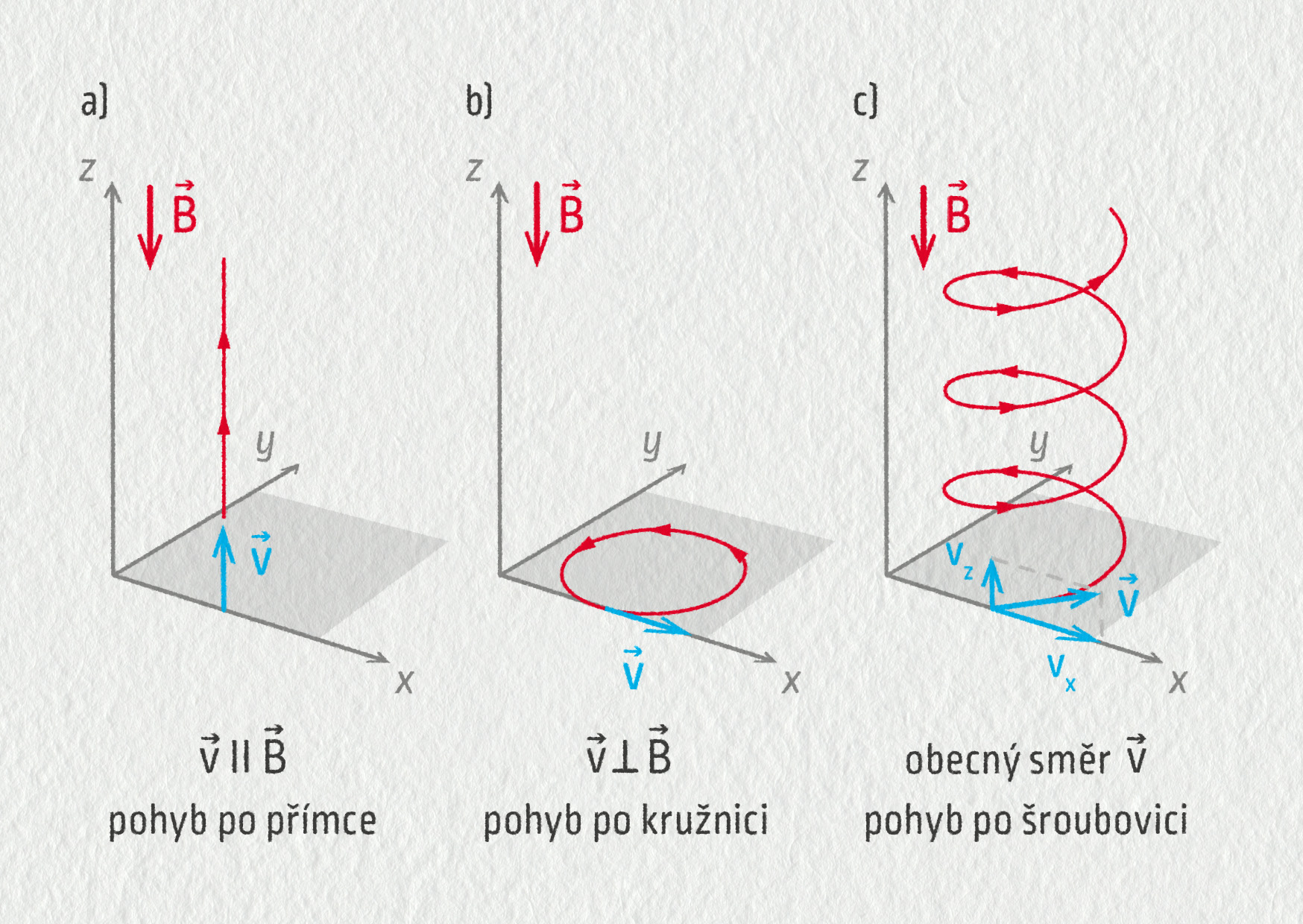
Zdroj
Na závěr se podíváme podrobněji na několik situací, kde se s magnetickou silou můžeme setkat.
Hallova sonda
Co se stane, necháme-li procházet proud destičkou z polovodiče typu N, která je umístěna v magnetickém poli? Situace je znázorněna na obrázku 19.29. Magnetická síla působí na pohybující se nabité částice (elektrony) a vychyluje je směrem k jedné straně destičky. Tím vzniká elektrické napětí, jehož velikost závisí na velikosti magnetické indukce ve směru kolmém na destičku. Hallova sonda nám tak umožňuje měřit magnetickou indukci. Můžete si to sami vyzkoušet v praktiku.
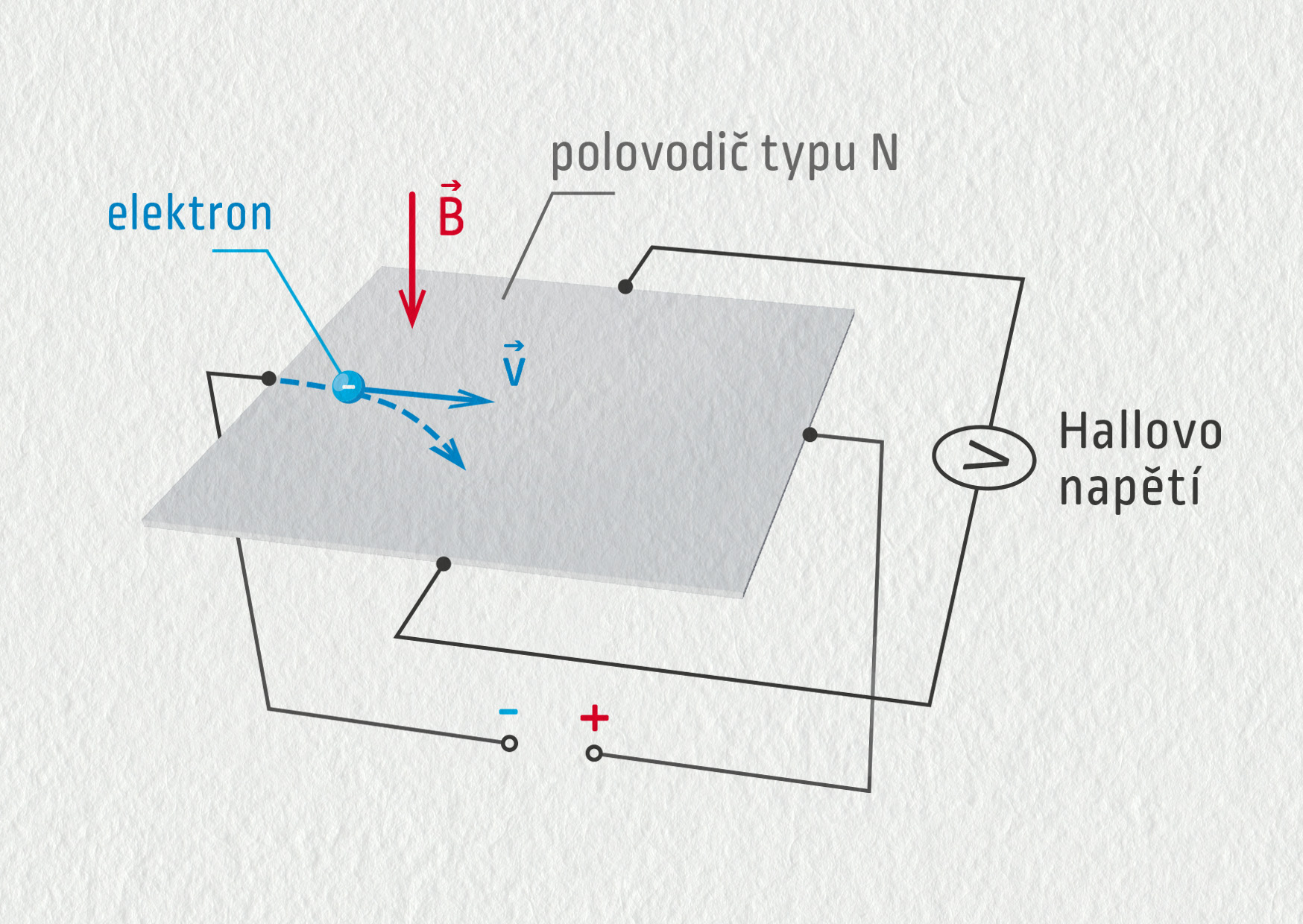
Zdroj
Urychlovač částic
Další využití nachází magnetická síla v urychlovačích částic. Jejich účelem je urychlit nabité částice na co největší rychlost a tím jim dodat co největší energii. K tomu se používá elektrické pole (viz kapitola 18). Magnetická síla má oproti elektrické jednu důležitou vlastnost. Tím, že je vždy kolmá na vektor rychlosti, nemůže měnit jeho velikost (jedná se o normálovou sílu), ale pouze směr. Magnetická síla tedy částice neurychluje, ale umožňuje udržet je na kruhové trajektorii.
Na obrázku 19.30 vidíte princip cyklotronu. Za vynález tohoto urychlovače obdržel v roce 1939 americký fyzik Ernest Orlando Lawrence Nobelovu cenu. Cyklotron je tvořen dvěma dutinami ve tvaru půlkruhu.
Mezi nimi je střídavé elektrické napětí, které částicím dodává energii při každém průletu. Nahoře a dole jsou póly velkého magnetu. V jeho magnetickém poli se částice pohybují po půlkružnicích s rostoucím poloměrem. Podstatné je, že perioda oběhu částic nezávisí na jejich rychlosti (jak dokážeme v řešeném příkladu).
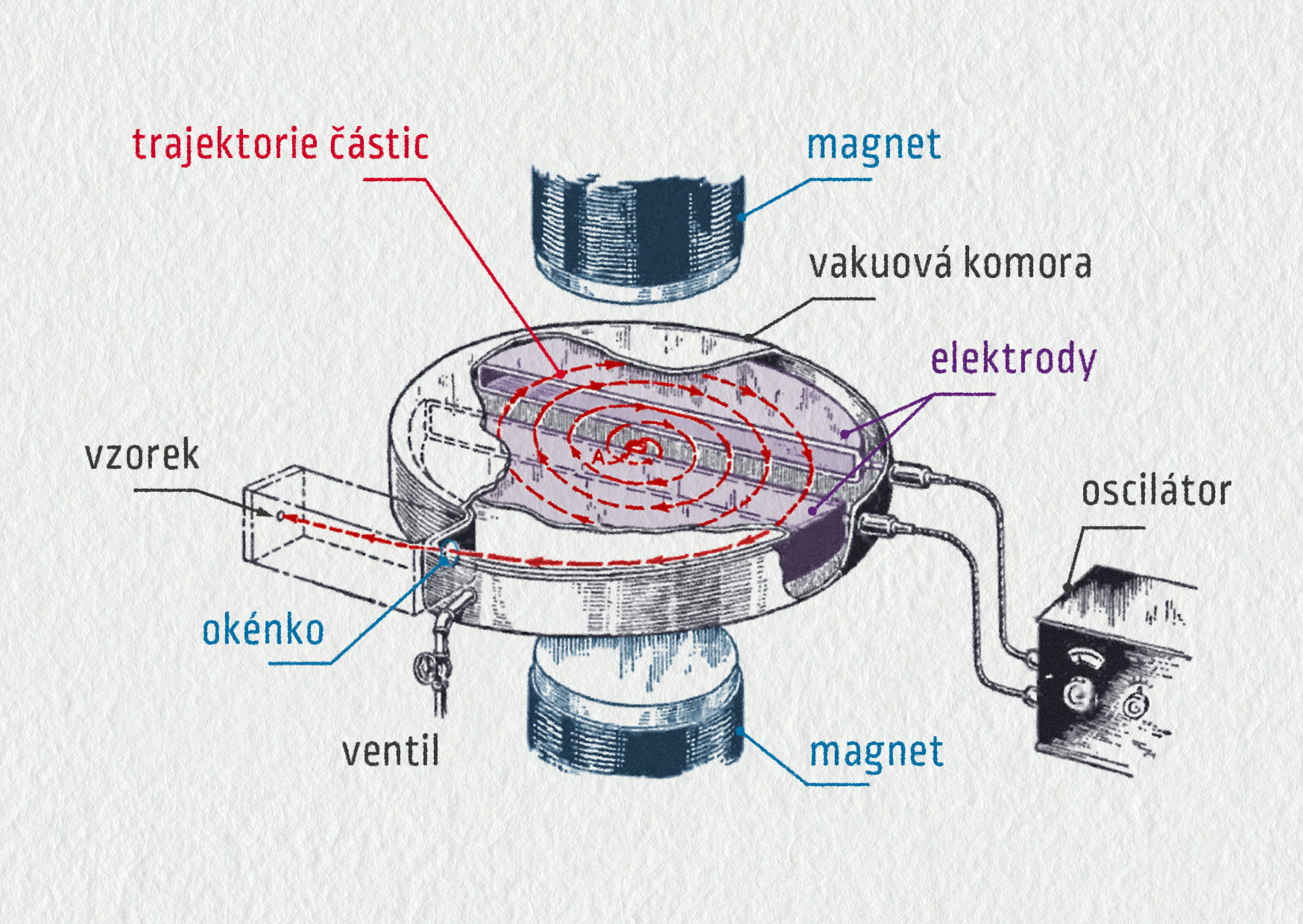
Zdroj
- Dokažte, že částice s nábojem \(q\) a rychlostí \(v\) se bude v magnetickém poli cyklotronu pohybovat po kružnici o poloměru \(r=mv/qB\). Nápověda: uvažte, že magnetická síla je v tomto případě dostředivou silou.
- Dokažte, že perioda oběhu částice v cyklotronu nezávisí na její rychlosti ani na poloměru kružnice. Platí \(T=2\pi m/qB\).
a) V cyklotronu se částice pohybuje tak, že její rychlost je vždy kolmá na vektor \(\Vec{B}\). Magnetická síla \(F=qvB\) tak tvoří sílu dostředivou, pro kterou platí \(F_\mathrm{D}=mv^2/r\). Gravitační síla zde nehraje roli a elektrická síla se uplatní pouze při urychlování částice, a o to nám teď nejde. Nyní stačí zapsat rovnost \(F=F_\mathrm{D}\) a odtud
\[ qvB = \frac{mv^2}{r} \]Vyjádřením neznámé \(r\) dostaneme \(r=mv/qB\).
b) Pro periodu při pohybu po kružnici platí \(T=2\pi r/v\). Dosazením za \(r=mv/qB\) (viz úloha a) dostaneme
\[ T = \frac{2\pi m}{qB}\;. \]Z periody snadno získáme i cyklotronovou frekvenci: \(f=1/T=qB/2\pi m\).
Prvního předchůdce cyklotronu postavil Ernest O. Lawrence roku 1930. Měl průměr jen 12 cm a protony v něm dosahovaly výstupní energie 80 keV.
- Vypočítejte výstupní rychlost protonů.
- Určete velikost magnetického pole cyklotronu.

Zdroj
a) Kinetická energie částice je \(E=\frac12mv^2\). Odtud vyjádříme \(v=\sqrt{2E/m}\). Než se pustíme do dosazování, musíme energii protonu převést na jouly pomocí elementárního náboje: \(E=80\ \mathrm{keV}=80\,000\ \mathrm{V}\cdot1{,}6\cdot10^{-19}\ \mathrm{C}=1{,}28\cdot10^{-14}\ \mathrm{J}\). Hmotnost protonu je \(m=1{,}67\cdot10^{-27}\ \mathrm{kg}\).
\[ v=\sqrt{\frac{2E}m}=3{,}9\cdot10^7\ \mathrm{m/s}\;. \]To je řádově desetina rychlosti světla, proto se v tomto případě nemusíme starat o relativistické efekty.
b) V předchozím příkladu jsme dokázali vztah pro poloměr kružnice při pohybu částice v magnetickém poli \(r=mv/qB\). Teď nám proto stačí z tohoto vztahu vyjádřit neznámou \(B\) a správně dosadit: \(B=mv/qr=6,8\ \mathrm{T}\).
Sluneční vítr
Sluneční vítr je proud nabitých částic (protonů, elektronů či iontů), které jsou uvolňovány ze sluneční atmosféry. Mají tak velkou rychlost (stovky kilometrů za sekundu), že uniknou z gravitačního pole Slunce.
Pokud částice slunečního větru zamíří směrem k Zemi, dostanou se do jejího magnetického pole. Zkusme naše znalosti o pohybu částic aplikovat na sluneční vítr v magnetickém poli Země. Je třeba vzít v úvahu, že zemské magnetické pole není homogenní.
Dokreslete do obrázku 19.32 možné trajektorie částic slunečního větru v zemském magnetickém poli. Kde budou částice vstupovat do atmosféry?
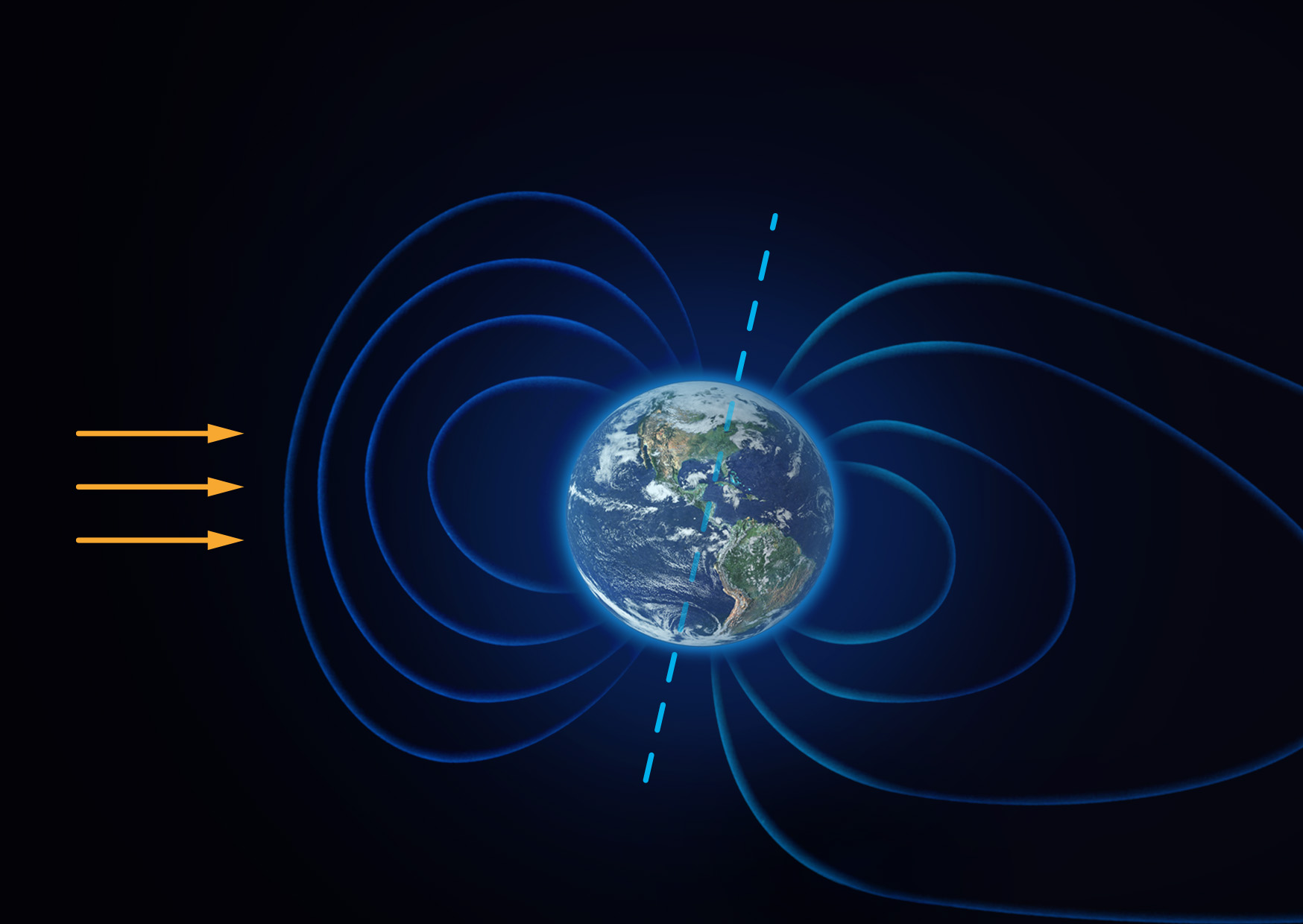
Zdroj
Částice vlétají do magnetického pole pod různými úhly. Velká část z nich se začne pohybovat po šroubovici podél indukčních čar. Indukční čáry jsou zakřivené a směřují do oblasti magnetických pólů. Proto se částice v polárních oblastech dostanou do atmosféry, kde ionizují molekuly vzduchu a vytváří polární záři.

Zdroj

Zdroj
Vodič v magnetickém poli
Na příkladu Hallovy sondy jsme viděli, že magnetická síla může působit i na částice pohybující se uvnitř vodiče. Představme si nyní kus přímého vodiče délky \(l\), kterým teče proud \(I\). Na pohybující se nabité částice ve vodiči působí síla o velikosti \(F=qvB\sin\alpha\). Tento vztah lze přepsat do podoby
\[ F = BIl\sin\alpha\;, \]neboť \(q=It\) a \(vt=l\). Uvažme také směr magnetické síly, který je vždy kolmý na \(\Vec{v}\). V případě vodiče je proto magnetická síla vždy kolmá na vodič. To je základním principem elektromotoru. Konstrukce a typy elektromotorů jsou popsány podrobněji v kapitole 20. Směr magnetické síly můžeme snadno ověřit také pomocí experimentu, jak ukazuje obrázek.

Zdroj

