Kinetická energie je druh energie, který souvisí s pohybovým stavem tělesa. Říkáme, že těleso, které se pohybuje rychlostí v, má kinetickou energii, a naopak těleso, které je v klidu, ji nemá. Jednoduchým způsobem můžeme přijít na to, jak ji vyjádřit.
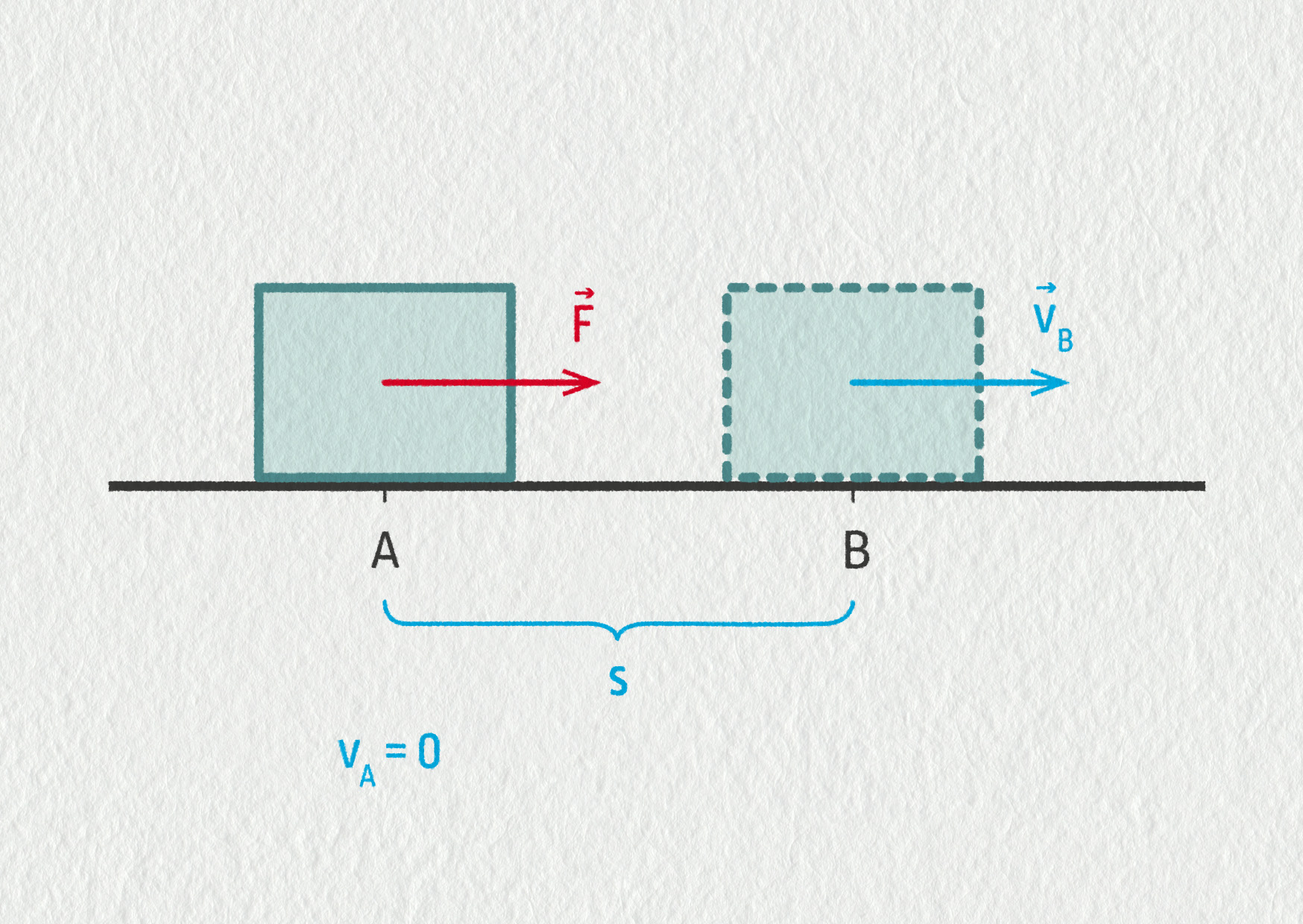
Uvažujme těleso zanedbatelných rozměrů, které je v klidu v bodě A (\(v_A=0\)). Účinkem výsledné konstantní síly \(\Vec{F}\) jej uvedeme do pohybu a v bodě B, kdy již urazí vzdálenost s, získá rychlost \(v_B\).
Zdroj
Síla F vykonala práci \(W_F=Fs\). Výsledná síla je přímo úměrná zrychlení tělesa \(F=ma\), pohyb je rovnoměrně zrychlený – tedy \(s=\frac{1}{2}at^2\). Po dosazení
\[W_F=Fs=ma\cdot\frac{1}{2}at^2=\frac{1}{2}ma^2t^2\]Protože rychlost pohybu rovnoměrně zrychleného bez počáteční rychlosti můžeme vyjádřit vztahem \(v=at\), lze napsat výsledný vztah pro vykonanou práci ve tvaru \(W_F=\frac{1}{2}mv_B^2\). Pravá strana tohoto vztahu závisí na druhé mocnině rychlosti a umožňuje nám definovat kinetickou energii hmotného bodu:
Vypočítejte kinetickou energii následujících hmotných bodů a těles. Předpokládejte, že kinetická energie tělesa se počítá stejně jako kinetická energie hmotného bodu.
- cyklista o hmotnosti 70 kg spurtující rychlostí 65 km/h;
- kulka o hmotnosti 8 g vystřelená ze samopalu rychlostí 705 m/s;
- meteoroid o hmotnosti 200 000 tun vstupující do atmosféry rychlostí 50 000 km/h.

Zdroj
- 11,4 kJ
- 2 kJ
- 1,9 ⋅ 1016 J
Vztah mezi prací a kinetickou energií
Předchozí odvození můžeme trochu zobecnit. Mezi prací vykonanou výslednou silou a změnou kinetické energie je úzký vztah:
Celková práce vykonaná na tělese je rovna změně jeho kinetické energie.
\[W=\Delta E_\mathrm{k}=\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2\]Na levé straně rovnice máme práci v joulech, na pravé straně rovnice kinetickou energii rovněž v joulech. Práce a kinetická energie spolu tedy úzce souvisí, mají dokonce stejnou jednotku. Obě jsou skalární veličiny.
Tento vztah nám ukazuje důležitou souvislost mezi konáním práce a změnou energie. Konání práce je totiž jedním ze způsobů přenosu energie mezi dvěma tělesy nebo systémy.
Představte si, že upustíte jablko. Jestliže jablko padá, jeho kinetická energie roste, a tíhová síla koná kladnou práci. Když jablko vyhodíte vzhůru, tíhová síla bude konat zápornou práci, a my budeme pozorovat, že jablko zpomaluje. Když tuto situaci zobecníme, můžeme říci, že kdykoliv je výsledná práce sil na těleso kladná, jeho rychlost roste. Naopak když je celková práce sil na těleso záporná, jeho rychlost klesá. Zkusme odvodit přesnou formulaci vztahu mezi prací a energií.
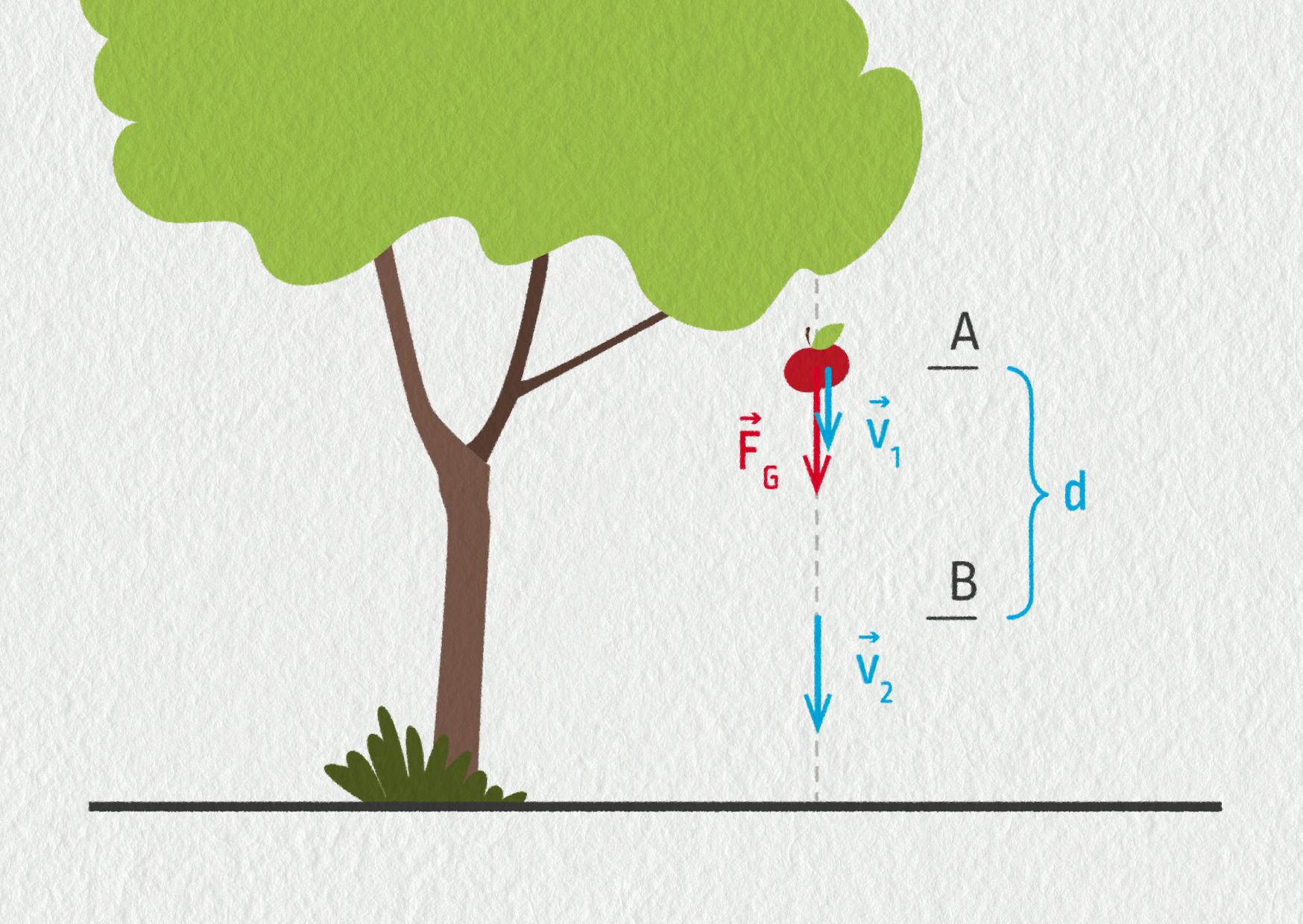
Uvažujme jablko o hmotnosti m padající ve vzduchu. Na jablko působí několik sil, ale my budeme uvažovat pouze tu největší z nich – tíhovou sílu \(\Vec{F}_\mathrm{G}\). Tato výsledná síla uděluje jablku konstantní zrychlení o velikosti \(a=g\) (tíhové zrychlení). Protože síla směřuje dolů a současně se jablko pohybuje také dolů, práce je kladná.
Zdroj
Uvažujeme-li počáteční rychlost jablka o velikosti v1 a poté, co jablko urazilo vzdálenost d, je jeho rychlost v2, můžeme na základě kinematiky rovnoměrně zrychleného pohybu sestavit dvě rovnice:
\[ \begin{aligned} d &= v_1t + \frac{1}{2}at^2\\ v_2 &= v_1 + at \end{aligned} \]Když z první rovnice vyjádříme čas t a dosadíme do druhé, získáme: \(v_2^2=v_1^2+2ad\).
Odtud pak vyjádříme:
\[2ad=v_2^2-v_1^2\]A protože zrychlení je podíl výsledné síly a hmotnosti, můžeme tento vztah přepsat jako:
\[2\frac{F}{m}d=v_2^2-v_1^2\]Vynásobíme-li rovnici hmotností m a vydělíme-li ji 2, dostaneme:
\[Fd=\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2\]Zde již vidíme práci vykonanou výslednou silou \(W=Fd\) a změnu kinetické energie mezi počátečním a koncovým okamžikem
\[\Delta E_\mathrm{k}=E_\mathrm{k2}-E_\mathrm{k1}=\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2\]neboť vztah pro výpočet velikosti kinetické energie tělesa v posuvném pohybu je \(E_\mathrm{k}=\frac{1}{2}mv^2\).
Potvrzujeme tedy vztah \(W=\Delta E_\mathrm{k}=\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2\).
Podle vztahu mezi prací a kinetickou energií můžeme psát:
\[W_F=\Delta E_\mathrm{k}=\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2=\frac{1}{2}mv_2^2=\frac{1}{2}\cdot74\ \mathrm{kg}\cdot(7{,}2\ \mathrm{m/s})^2=1{,}9\ \mathrm{kJ}\]Vykonaná práce je minimálně 1,9 kJ, neboť při každém kroku se též těžiště člověka zvedne a poté zase klesne o několik centimetrů,, k čemuž je potřeba konat práci navíc.
Jak určit práci v případě několika působících sil?
Jestliže na těleso působí více než jedna síla, celková práce je rovna součtu prací vykonaných jednotlivými silami samostatně. Jestliže tedy síla \(\Vec{F}_1\) koná práci \(W_1\), síla \(\Vec{F}_2\) koná práci \(W_2\) atd., pak můžeme pro celkovou práci zapsat:
\[W_\mathrm{celkem}=W_1+W_2+\dots+W_n=\sum_{i=1}^n W_i\]Celkovou vykonanou práci také můžeme vypočítat tak, že vypočítáme práci vykonanou výslednou silou \(W_\mathrm{celkem}=Fs\cos\alpha\), kde F značí výslednici všech působících sil.
Síla \(\Vec{F}\) je totiž výslednicí všech sil působících na těleso a úhel α je velikost úhlu mezi posunutím a výslednou silou.
\[W_\mathrm{celkem}=\sum_{i=1}^n W_i=\sum_{i=1}^n\Vec{F}_i\cdot\Vec{s}=\Vec{s}\cdot\sum_{i=1}^n\Vec{F}_i=\Vec{s}\cdot\Vec{F}=Fs\cos\alpha\]Zkouška brzd osobního automobilu o hmotnosti 1 500 kg probíhá na vodorovném úseku zkušebního polygonu. Na úseku o délce 35 m se změní rychlost automobilu z původních 108 km/h na konečných 90 km/h.
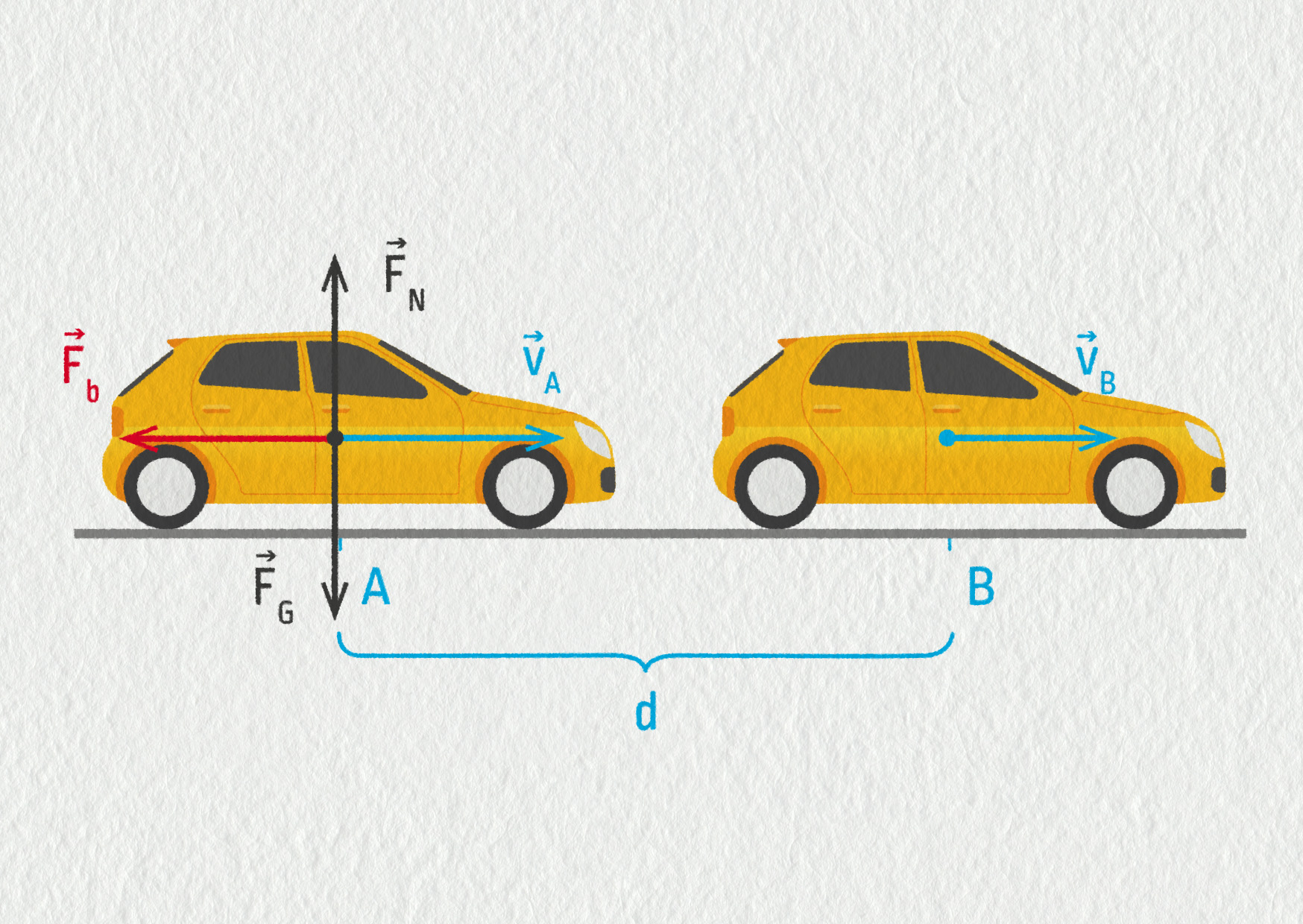
- Nakreslete schéma situace včetně všech sil působících na automobil. Brzdnou sílu a odporové síly předpokládejme konstantní a zakresleme je jako jednu sílu.
- Vypočítejte velikost brzdné síly působící na automobil pomocí prací a energií.
a) Schéma:
Zdroj
b) Použijeme vztah ukazující na souvislost mezi prací a změnou kinetické energie:
\[ \begin{aligned} \sum W_F &= \Delta E_\mathrm{k}\\ W_\mathrm{G} + W_\mathrm{N} + W_\mathrm{b} &= \frac{1}{2}mv_B^2 - \frac{1}{2}mv_A^2\\ 0+0-F_\mathrm{b}d &= \frac{1}{2}m(v_B^2-v_A^2)\\ F_\mathrm{b} &= \frac{m(v_A^2-v_B^2)}{2d} = \frac{1500\cdot(30^2-25^2)}{2\cdot35}\ \mathrm{N}=5{,}1\ \mathrm{kN} \end{aligned} \]
