Co je to potenciální energie? Jaké má formy? Kde se s ní setkáme? Opět si tento pojem vysvětleme na příkladu s konáním práce. Víme, že mechanická síla může konat práci, a tím může například zvětšit kinetickou energii tělesa. Při působení více sil se ale stává, že určitá síla koná kladnou práci, aniž by se zvětšovala kinetická energie tělesa. Pojďme se na tyto příklady podívat podrobněji…
Nejprve si představme situaci, ke které dochází při střelbě z luku. Při napínání luku vykoná síla ruky docela velkou práci, luk se napne, ale zůstává v klidu. Vykonaná práce však zůstala „uložena“ v novém uspořádání luku (je napnutý). Tuto situaci můžeme popsat tak, že se zvedla potenciální energie pružnosti luku. Při výstřelu pak můžeme tuto energii použít k urychlení šípu. Stejným způsobem, tedy pomocí deformace pružiny, uvolňujeme energii při výstřelu.
V druhém příkladu si zkusme představit knihu, kterou bereme ze stolu a ukládáme ji do knihovny. Na začátku i na konci pohybu je kniha v klidu (žádná pohybová energie), přesto jsme vykonali určitou práci při jejím zvedání do police v knihovně. Můžeme říci, že jsme vykonanou práci „uložili“ do potenciální energie v tíhovém poli. Když bude kniha padat na zem, tato energie se postupně přemění na kinetickou energii.
Další příklady, kdy se energie ukládá ve formě potenciální energie, si ukažme v následující galerii.

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj
Pojďme si dvě základní situace popsat detailněji.
Potenciální energie pružnosti
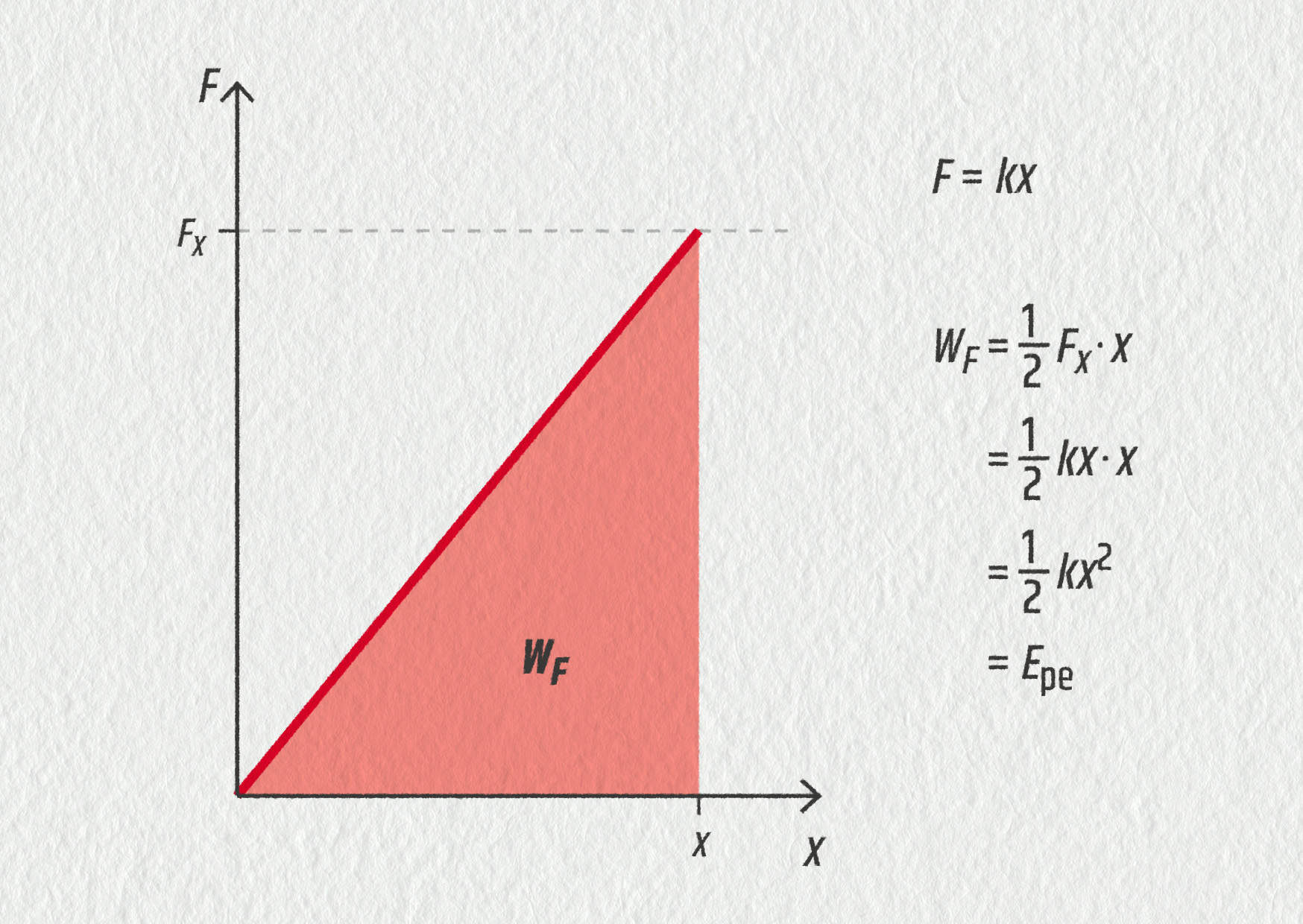
Vezměme pružinu o délce \(l_0\) a zavěsme ji na háček. Když na ni budeme dále zavěšovat závaží s rostoucí hmotností, budeme na její konec působit čím dál větší silou, a pružina se bude prodlužovat. Z rovnováhy sil můžeme usoudit, že pružina působí na závaží stejně velkou silou, jakou je napínána. Tahová síla \(\Vec{F}_\mathrm{tah}\) pružiny je přímo úměrná jejímu prodloužení x: \(F_\mathrm{tah}=kx\). Zakreslíme-li tuto závislost do grafu, získáme graf přímé úměrnosti.
Zdroj
Protože velikost práce vykonané touto silou je rovna obsahu plochy pod grafem, vidíme, že
\[W=F_\mathrm{tah}x=\frac{1}{2}kx\cdot x=\frac{1}{2}kx^2 = E_\mathrm{pe}\]Potenciální energie pružnosti závisí na velikosti deformace x pružiny a na její tuhosti k neboli na tom, jak snadno nebo naopak obtížně ji lze deformovat.
Potenciální energie pružnosti \(\displaystyle E_\mathrm{pe}=\frac{1}{2}kx^2\).
Potenciální tíhová energie
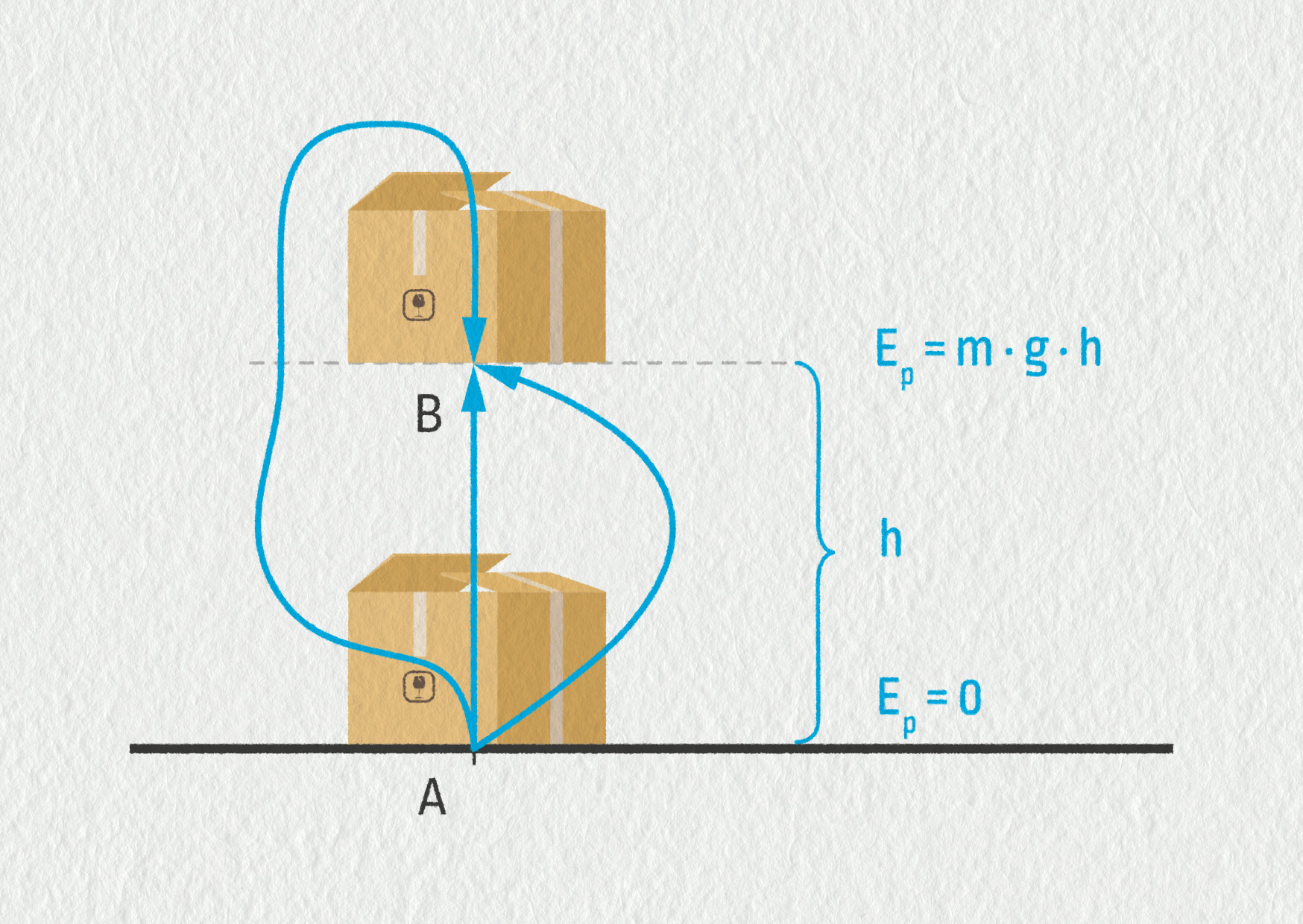
Představte si, že zvedáte krabici o hmotnosti m z podlahy do výšky h (viz obrázek).
Zdroj
Musíte působit proti gravitaci silou o velikosti \(mg\), a na dráze \(h\) tak vykonáte práci \(W=mgh\). Dá se ukázat, že vykonaná práce závisí jen na výšce h, nikoliv na zvolené trajektorii (viz obrázek). Díky tomu můžeme definovat potenciální (polohovou) energii \(E_\mathrm{p}\) jakožto práci potřebnou ke zvednutí tělesa z vybraného místa do výšky \(h\) nad ním.
Polohová energie v tíhovém poli Země \(E_\mathrm{p}=mgh\).
Polohová energie není určena jednoznačně, závisí na naší volbě referenčního místa (nulové výšky). Hladinu, kde bude energie nulová, si můžeme zvolit zcela libovolně. V našem příkladu jsme zvolili \(E_\mathrm{p}=0\) na podlaze (bod A).
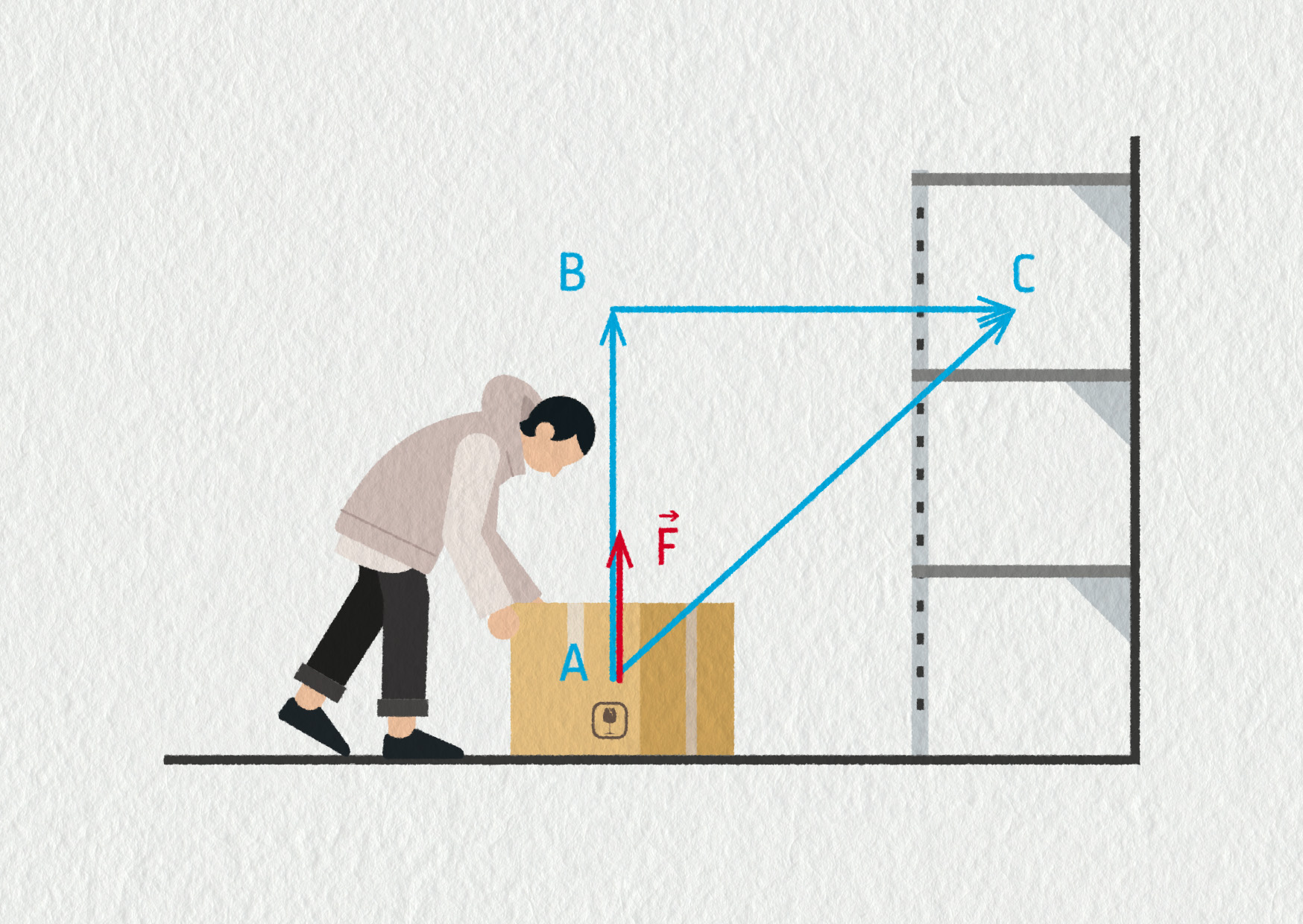
Bednu o hmotnosti 15 kg jsme ze země zvedli do police ve výšce 1,2 m. Vypočítejte vykonanou práci, pokud pohyb probíhal:
- nejdříve 1,2 m svisle a potom 1 m vodorovně (trajektorie ABC),
- po nejkratší spojnici z A do C.
Zdroj
- \(W_{ABC}=W_{AB}+W_{BC}=mgh_{AB}+0=mgh_{AB}=176\ \mathrm{J}\)
- \(W_{AC}=F\cdot|AC|\cdot\cos\alpha=F\cdot|AB|=mgh_{AB}=176\ \mathrm{J}\)
Velikost vykonané práce při zvedání bedny v tíhovém poli země nezávisí na tvaru trajektorie a má vždy stejnou velikost.

Zdroj
Jestliže nyní krabici upustíte, bude naopak tíhová síla konat práci a urychlovat krabici směrem k zemi. Vykonanou práci jsme si tedy „uložili“ pomocí potenciální energie v tíhovém poli. Jestli jezdíte rádi na kole, je vám jasné, jakou práci vykonáte, když stoupáte do kopce, a část této „uložené“ energie pak získáte při sjezdu zpět.
Konzervativní a nekonzervativní síly
Viděli jsme tedy, že vykonanou práci můžeme uložit do různých forem potenciální energie a poté si ji vyzvednout ve formě jiné energie. Ne vždy to však je možné.
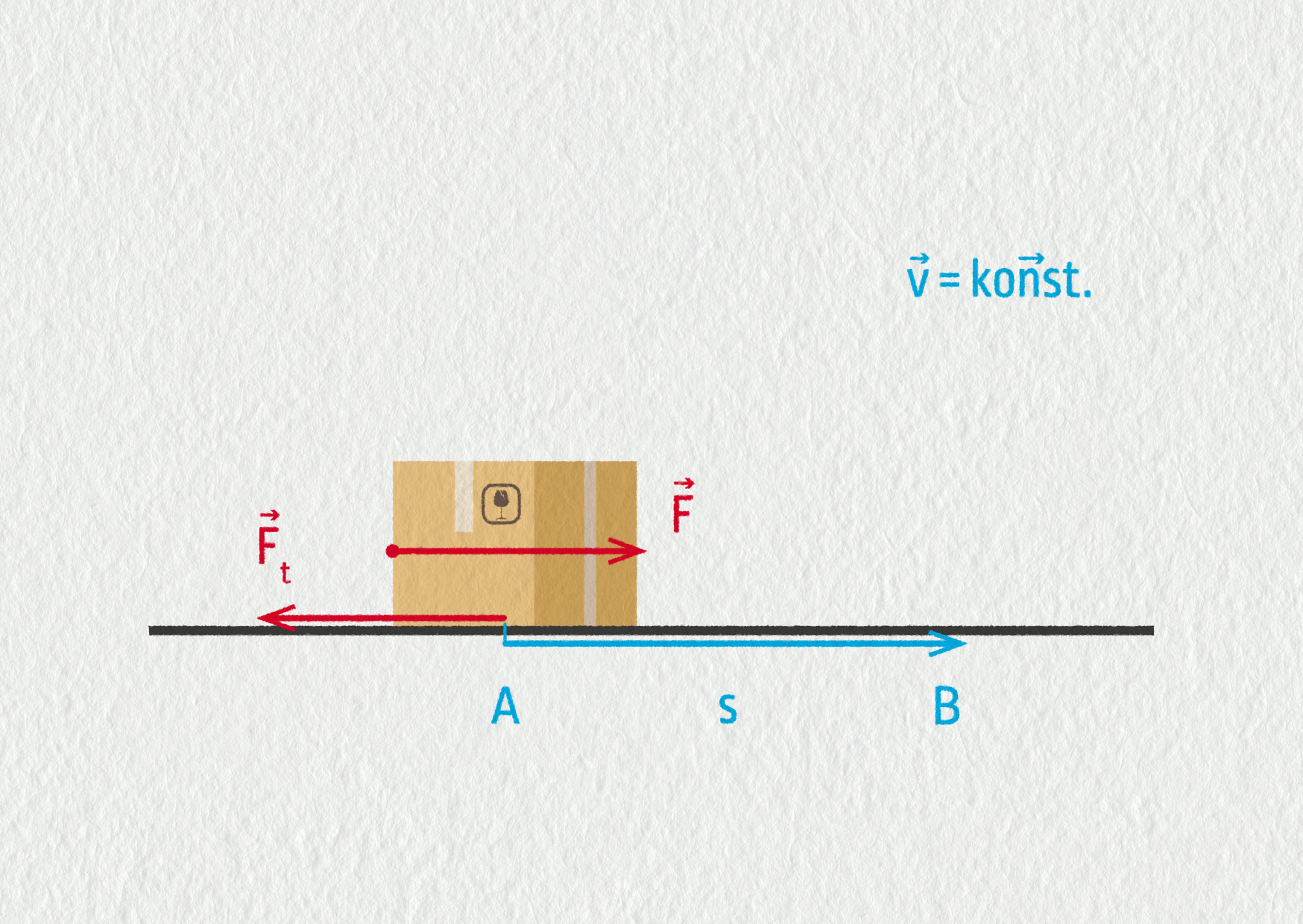
Tuto úvahu nemůžeme provést pro jakoukoliv sílu. Například když posunujeme naši bednu po vodorovné podlaze z A do B (viz obrázek 6.26), musíme překonávat třecí sílu. Čím bude trajektorie delší, tím větší práci budeme muset vykonat. Vidíme, že práce při posunutí z bodu A do B nyní závisí na zvolené trajektorii. Proto neexistuje potenciální energie třecí síly. A pokud bednu vrátíme zpět do bodu A, vykonaná práce se nám nevrátí tak, jako se to stane v tíhovém poli Země.
Zdroj
Když přestaneme na bednu tlačit, zastaví se. Vykonanou práci nelze přeměnit na kinetickou energii, protože již byla přeměněna na jiné formy energie – došlo k zahřátí podlahy i samotné bedny.
Podle uvedeného principu můžeme rozlišit tzv. konzervativní a nekonzervativní síly. Konzervativní síly nám umožní energii „uschovat“, zatímco při práci nekonzervativních sil se vždy nějaká část energie mění na jiné druhy energie, například teplo.
Zapišme to přehledně do tabulky:
| Konzervativní síly | Nekonzervativní síly |
|---|---|
| Práce nezávisí na trajektorii | Práce závisí na trajektorii |
| Existuje potenciální energie | Neexistuje potenciální energie |
| Příklady: gravitační síla, tíhová síla, elektrická síla, síla pružnosti | Příklady: třecí síla, odporová síla vzduchu |
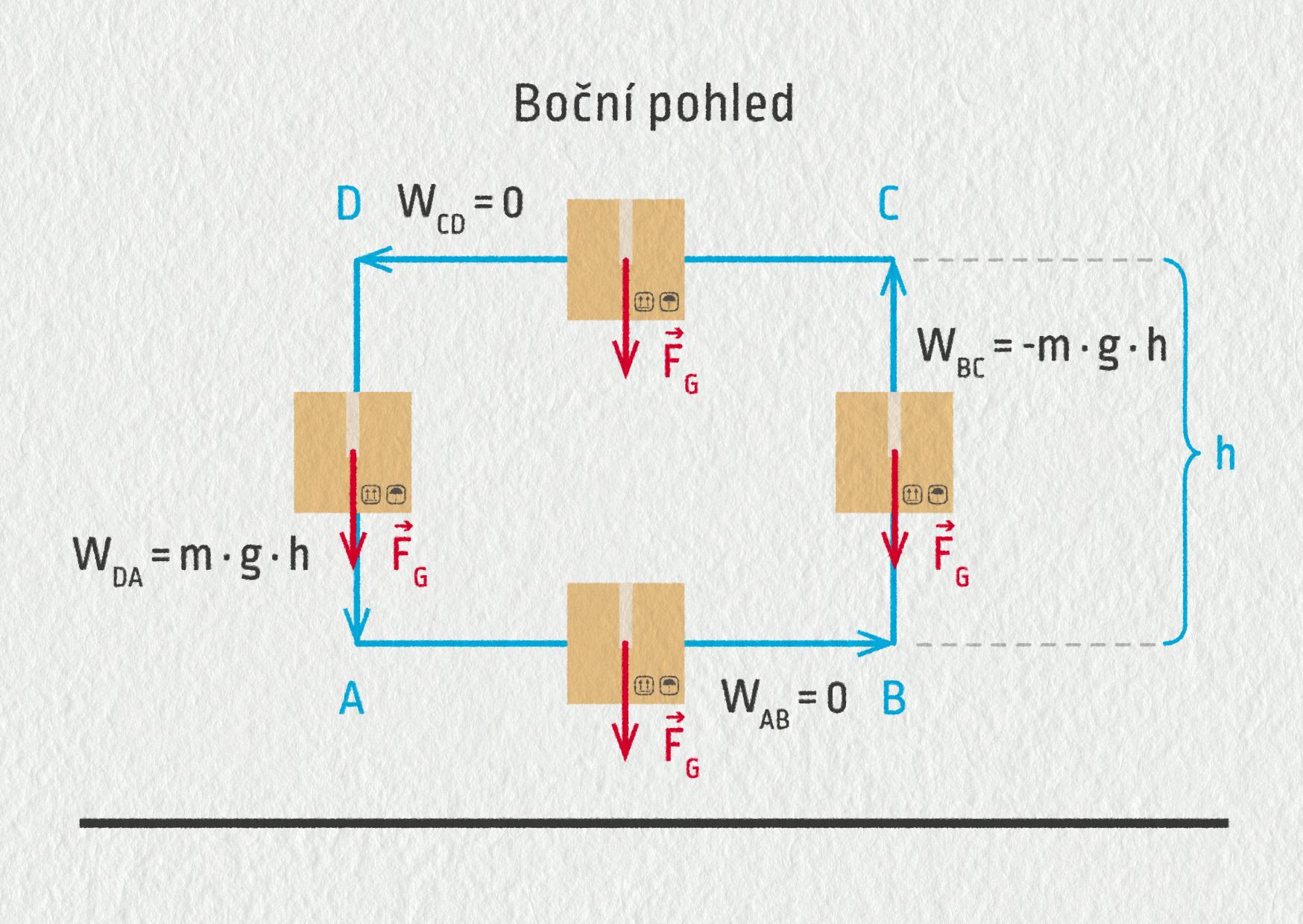
Velmi dobře je rozdíl mezi konzervativní a nekonzervativní silou vidět, jestliže porovnáme posunování předmětu po uzavřené křivce. Vezměme například práci vykonanou tíhovou silou při přesouvání krabice po křivce dle následujícího obrázku.
Zdroj
Při vodorovném přenášení krabice z bodu A do bodu B je práce vykonaná tíhovou silou nulová \(W_{AB}=0\), protože vektor síly je kolmý k posunutí. Stejně tak mezi body C a D \(W_{CD}=0\). Od bodu B do bodu C krabici zvedáme, tudíž konáme práci my a práce vykonaná tíhovou silou je záporná \(W_{BC}=-mgh\). Naopak mezi body D a A je tato práce kladná, protože tíhová síla působí ve směru posunutí \(W_{DA}=mgh\). Celková práce vykonaná tíhovou silou na této uzavřené dráze je pak rovna součtu:
\[W_\mathrm{G}=W_{AB}+W_{BC}+W_{CD}+W_{DA}=0-mgh+0+mgh=0\]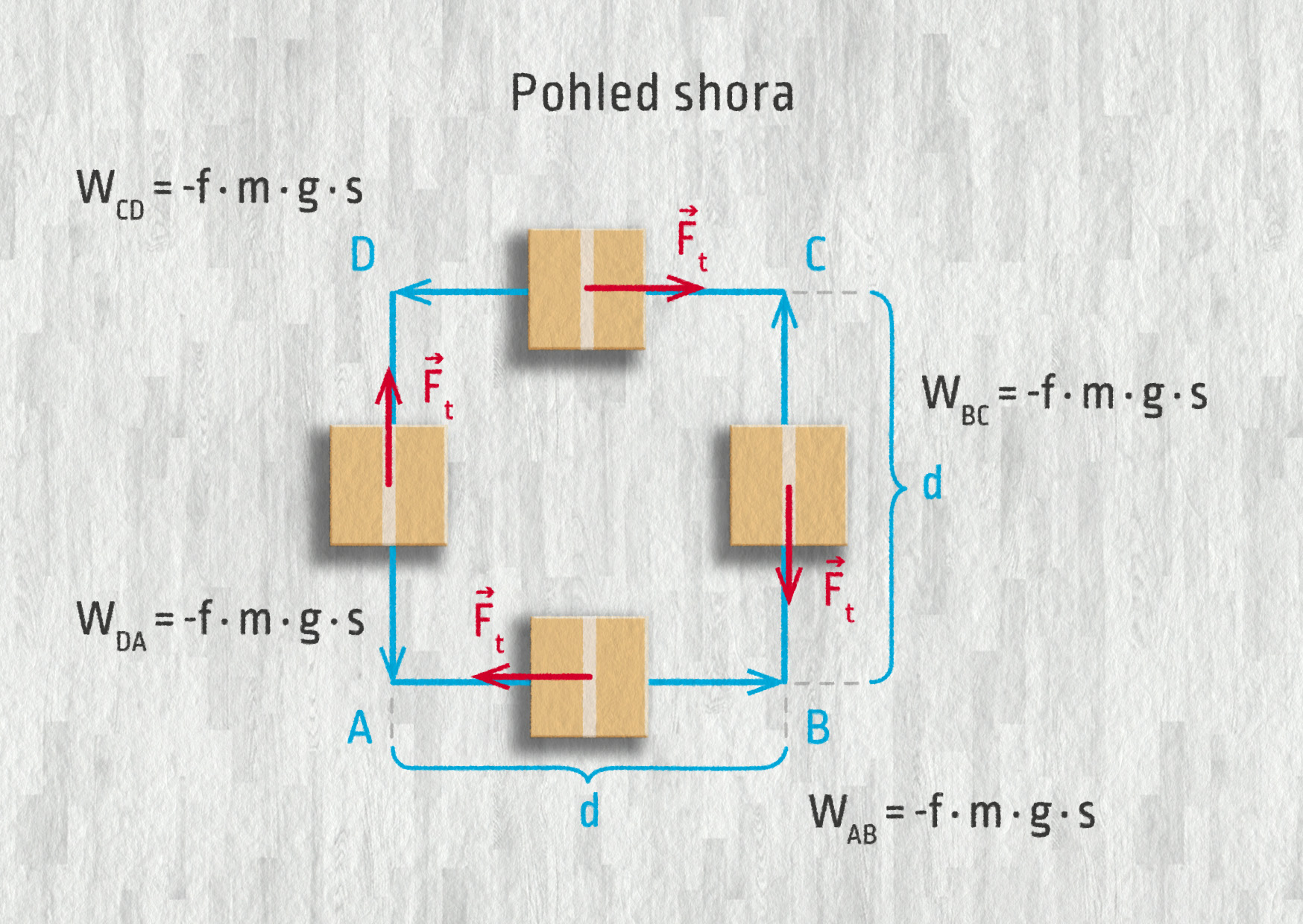
Zdroj
Jakmile ale budeme posunovat krabici po podlaze (viz obrázek), situace je zcela jiná. Třecí síla vykonává v každém jednotlivém úseku zápornou práci o velikosti \(W_\mathrm{t}=-fmgd\). Celkově pak na uzavřené dráze dostáváme.
\[W_\mathrm{t}=W_{AB}+W_{BC}+W_{CD}+W_{DA}=\] \[-fmgd+(-fmgd)+(-fmgd)+(-fmgd)=\] \[-4fgmd\]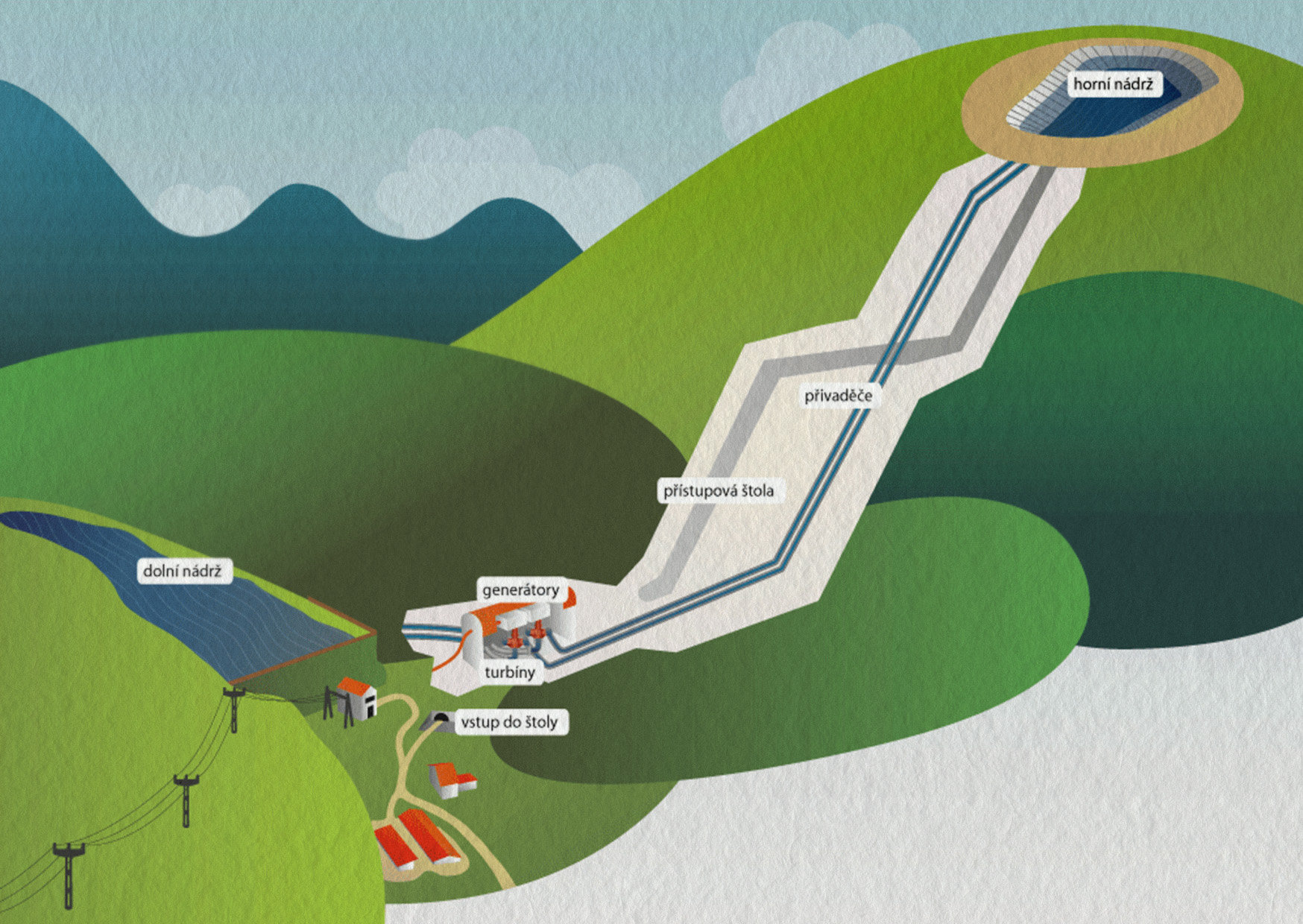
Zdroj
Přečerpávací vodní elektrárny představují jediný technicky známý způsob uskladnění vyrobené elektrické energie prostřednictvím potenciální energie vody. Jejich charakteristickým rysem jsou dvě zásobní nádrže – dolní a horní spojené tlakovými přivaděči. Soustrojí elektrárny je tvořeno čerpadlem, vodní turbínou a elektrickým motorgenerátorem na společném hřídeli. V čase nízkého zatížení a nadbytku elektřiny v soustavě odebírá soustrojí elektřinu, a přečerpává vodu z dolní do horní zásobní nádrže. V čase výkonnostní špičky, když je energie v síti nedostatek, tato voda pohání turbínu s generátorem a vrací naakumulovanou energii do rozvodné sítě. Na 1 kW vyrobené elektrické energie spotřebuje elektrárna v čerpadlovém provozu mimo špičku přibližně 1,3 kW.
Velikou výhodou přečerpávacích elektráren je jejich schopnost přecházet z režimu čerpání do režimu výroby elektrické energie a naopak v řádu několika minut, a tak dynamicky reagovat na aktuální zátěž energetické sítě.
Zdroj: obrázek http://edu.techmania.cz/cs/veda-v-pozadi/663, text: Obnovitelné zdroje energie (Simopt).

