Když studujeme pohyb nějakého tělesa v blízkosti země (tíhová síla je síla konzervativní), všimneme si, že polohová energie a kinetická energie na sobě nejsou nezávislé. Při volném pádu klesá polohová energie a roste kinetická energie. Po odpalu baseballového míčku naopak klesá kinetická energie a roste polohová energie tělesa. Jejich součet \(E_\mathrm{m}=E_\mathrm{p}+E_\mathrm{k}\), zvaný mechanická energie, však zůstává po celou dobu pohybu konstantní; za podmínky, že na těleso působí pouze konzervativní síly. Tento princip vyjadřuje zákon zachování mechanické energie.
Mechanická energie soustavy se zachovává, pokud v soustavě působí jen konzervativní síly.
\[E_\mathrm{m}=E_\mathrm{p}+E_\mathrm{k}\]Pomocí tohoto zákona můžeme mnohem snadněji řešit mnoho úkolů, které by při použití Newtonových zákonů byly matematicky podstatně složitější. Nemusíme se zabývat tím, jak se těleso dostalo do konečné polohy, stačí porovnat výchozí a konečný stav z hlediska energií. Pojďme si to ukázat na několika příkladech.
- S jakou rychlostí dopadne na zem pétanquová koule mající hmotnost 760 g, jestliže hráči upadne z ruky, kterou má volně podél těla (počáteční výška koule je 85 cm)?
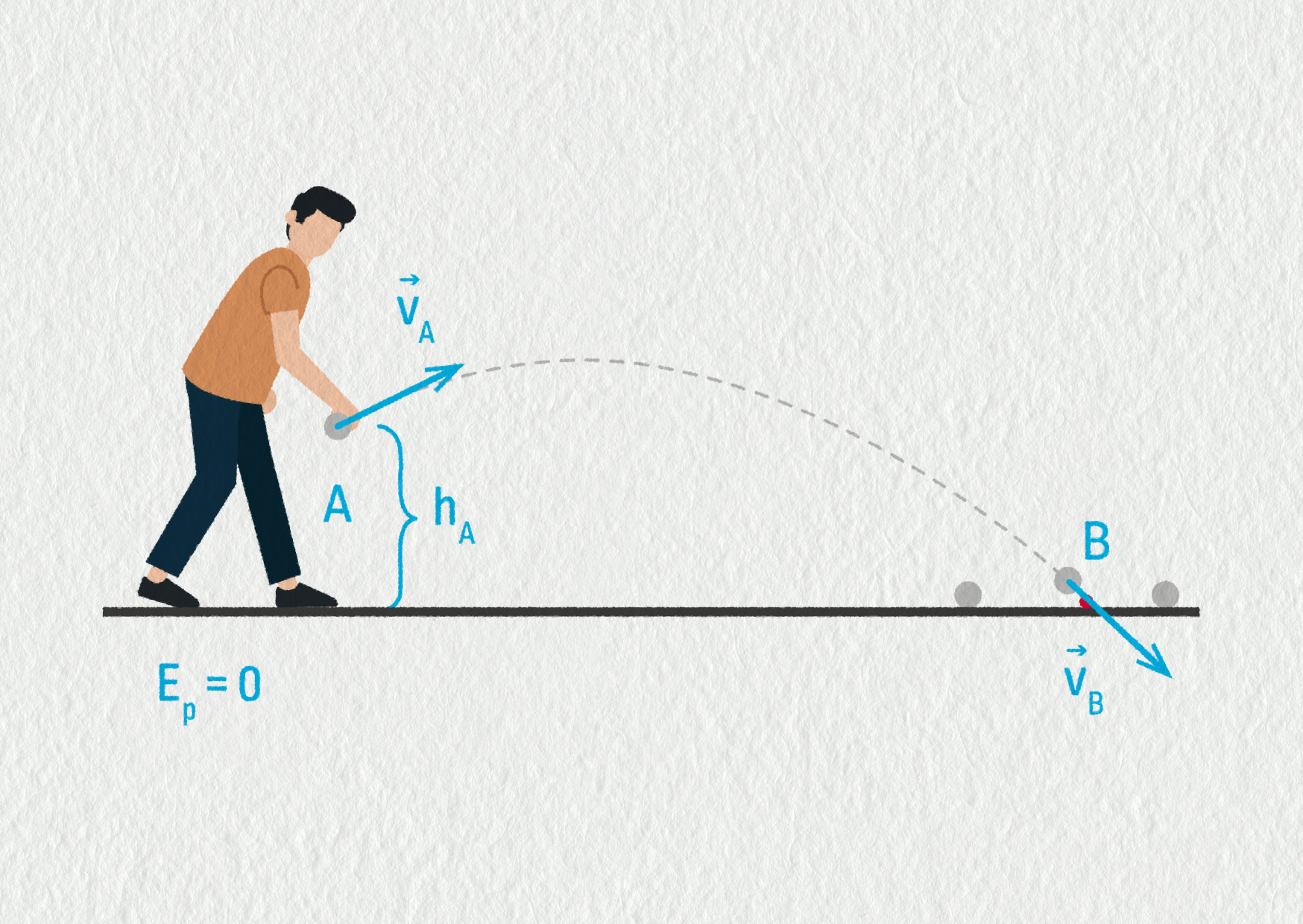
- S jakou rychlostí dopadne stejná pétanquová koule, jestliže je vržena hráčem z výšky 1,10 m nad zemí a na začátku pohybu má rychlost 6,3 m/s (viz obrázek)?
Zdroj
a) Podle zákona zachování mechanické energie je součet polohové a kinetické energie konstantní. Koule, kterou hráč drží v ruce (výška 85 cm nad zemí), má tedy tyto energie:
\[ \begin{aligned} E_{\mathrm{p}A} &= mgh = 0{,}760\cdot9{,}81\cdot0{,}85\ \mathrm{J}=6{,}3\ \mathrm{J}\\ E_{\mathrm{k}A} &= \frac{1}{2}mv_A^2 = 0\ \mathrm{J} \end{aligned} \]Toto celkové množství mechanické energie 6,3 J se zachovává a v okamžiku dopadu koule na zem má koule tyto energie: \(E_{\mathrm{p}B}=0\ \mathrm{J}\) a \(E_{\mathrm{k}B}=\frac{1}{2}mv_B^2=6{,}3\ \mathrm{J}\). Polohová energie \(E_\mathrm{p}\) se přeměnila na kinetickou \(E_\mathrm{k}\), ale jejich součet zůstal zachován. Píšeme tedy:
\[ \begin{aligned} E_{\mathrm{m}A} &= E_{\mathrm{m}B}\\ mgh+0 &= 0+\frac{1}{2}mv_B^2 \end{aligned} \]Pro rychlost dopadu koule pak můžeme vyjádřit \(v_B=\sqrt{2gh}=4{,}1\ \mathrm{m/s}\).
b) V případě, že je koule vržena určitou rychlostí šikmo vzhůru, postupujeme stejným způsobem. Celková mechanická energie na začátku vrhu je rovna celkové mechanické energii koule při dopadu na zem.
\[ \begin{aligned} E_{\mathrm{m}A} &= E_{\mathrm{m}B}\\ mgh+\frac{1}{2}mv_A^2 &= 0+\frac{1}{2}mv_B^2 \end{aligned} \]Pro velikost rychlosti dopadu koule pak platí: \(v_B=\sqrt{2gh+v_A^2}=\sqrt{2\cdot9{,}81\cdot1{,}1+6{,}3^2}\ \mathrm{m/s}=7{,}8\ \mathrm{m/s}\).
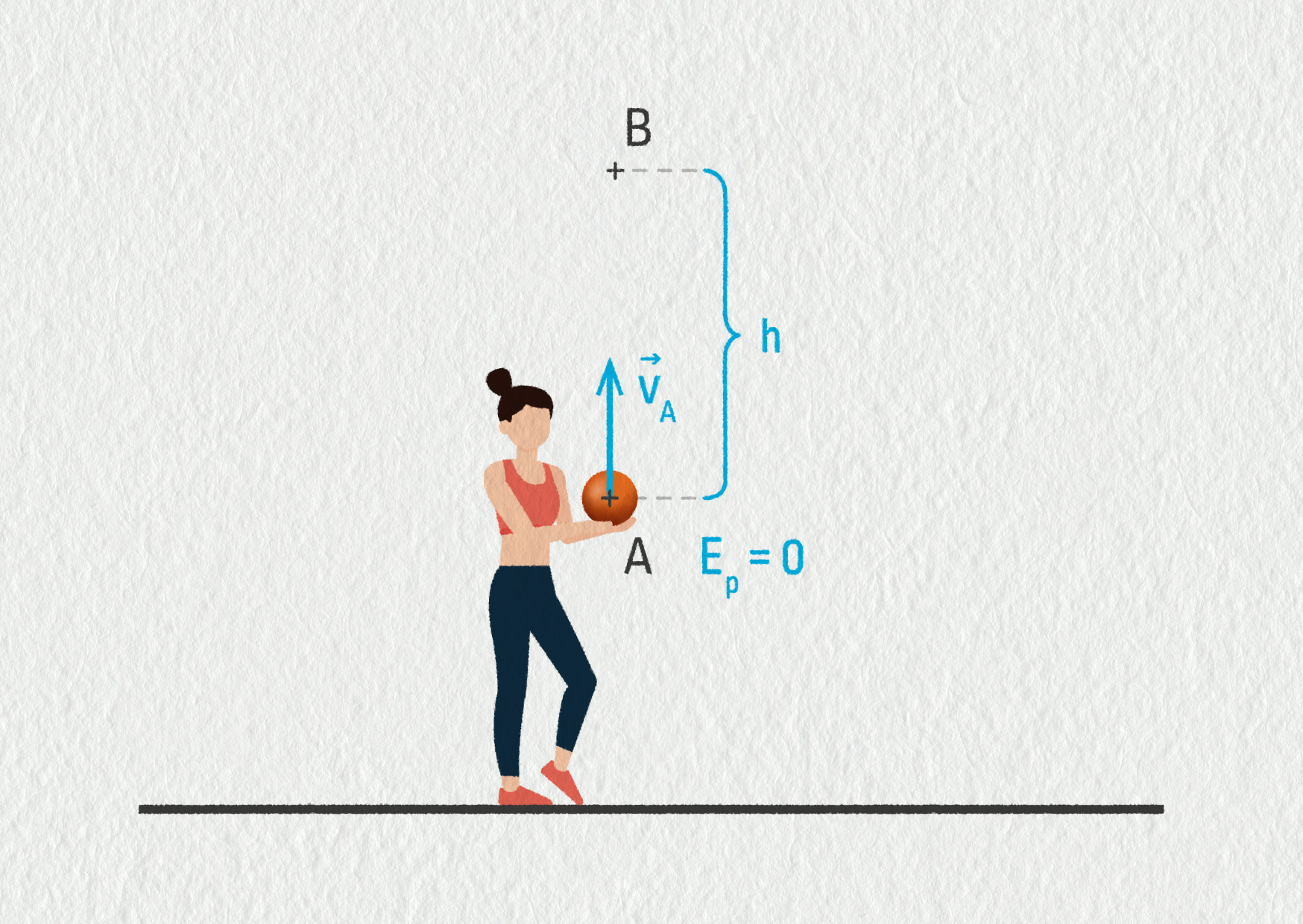
Zdroj
Opět vyjdeme ze zákona zachování energie. Mechanická energie je v počátečním bodě A a v koncovém bodě B stejná. Výchozí bod A volíme jako místo s nulovou polohovou energií \(E_\mathrm{p}=0\). Naopak v nejvyšším bodě B se míč zastaví, jeho kinetická energie bude nulová a poté začne padat dolů. Vyjádříme je takto:
\[ \begin{aligned} E_{\mathrm{m}A} &= E_{\mathrm{m}B}\\ \frac{1}{2}mv_A^2 &= 0+mgh \end{aligned} \]Pro maximální výšku vyhozeného míče pak můžeme vyjádřit:
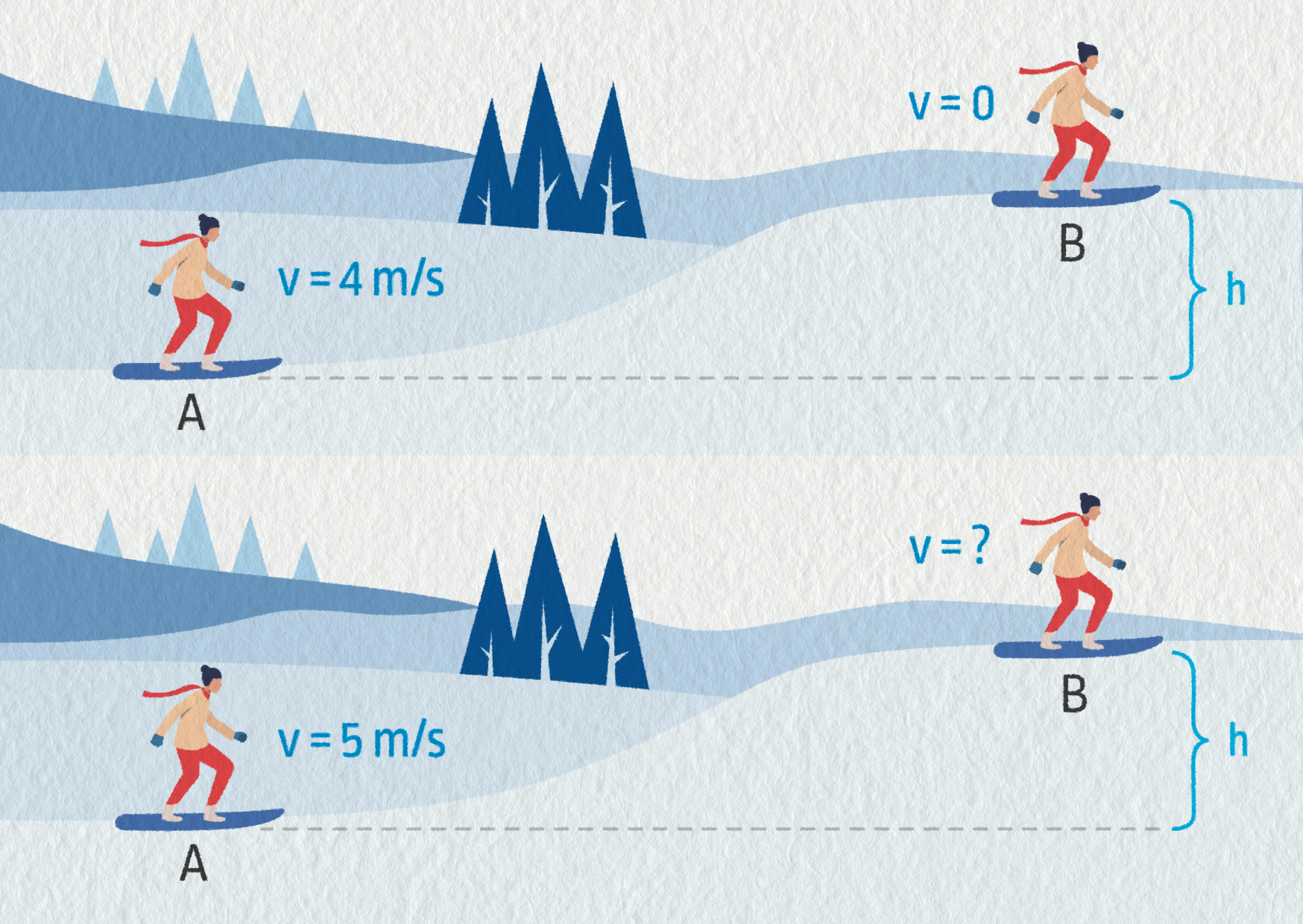
\[h=\frac{v_A^2}{2g}=\frac{12{,}5^2}{2\cdot9{,}81}\ \mathrm{m} = 8{,}0\ \mathrm{m}\]Snowboardista se pohybuje po vodorovné dráze rychlostí 4 m/s. Tato rychlost postačuje k tomu, aby se vyhoupl na malý kopec a zastavil se na něm (bod B, viz obrázek). Když se bude na začátku pohybovat rychlostí 5 m/s, jakou bude mít rychlost na vrcholu kopce?
Zdroj
Nejprve si vypočítáme výšku kopce, na který se snowboardista dostane při počáteční rychlosti 4 m/s. Ze zákona zachování mechanické energie vyplývá, že jeho mechanická energie v bodě A i B je stejná. Zvolme bod A jako místo s nulovou potenciální energií, a dostáváme tedy:
\[ \begin{aligned} E_{\mathrm{m}A} &= E_{\mathrm{m}B}\\ \frac{1}{2}mv_A^2 &= 0+mgh \end{aligned} \]Pro výšku kopce h získáme:
\[h=\frac{v_A^2}{2g}=\frac{4{,}0^2}{2\cdot9{,}81}\ \mathrm{m} = 0{,}82\ \mathrm{m}\]Jestliže při druhém pokusu jede na začátku (bod A) již rychlostí 5 m/s, bude mít tedy větší mechanickou energii a v bodě B mu bude zbývat ještě určité množství kinetické energie. Opět píšeme:
\[ \begin{aligned} E_{\mathrm{m}A} &= E_{\mathrm{m}B}\\ \frac{1}{2}mv_A^2 &= \frac{1}{2}mv_B^2+mgh \end{aligned} \]odkud pak vyjádříme výslednou rychlost na vrcholu kopce:
\[ \begin{aligned} \frac{1}{2}v_A^2 &= \frac{1}{2}v_B^2+gh\\ v_B^2 &= v_A^2-2gh\\ v_B &= \sqrt{v_A^2-2gh} = 3{,}0\ \mathrm{m/s} \end{aligned} \]Odhadněte na základě zákona zachování mechanické energie, jak vysoko může skokan o tyči vyskočit.

Zdroj
Skokan o tyči (hmotnost \(m=75\ \mathrm{kg}\)) se nejprve rozeběhne rychlostí přibližně 10 m/s. Má tedy na začátku pouze kinetickou energii. Jeho potenciální tíhová energie je nulová, pokud si zvolíme nulovou hodnotu této energie ve výšce jeho těžiště (viz obrázek).

Zdroj
Kinetická energie soustavy skokan–tyč \(E_{\mathrm{k}A}\) je následně přeměněna na potenciální energii pružnosti tyče \(E_\mathrm{pe}\) (deformace tyče) a poté přeměněna na potenciální energii v tíhovém poli Země \(E_{\mathrm{p}B}\). Za předpokladu, že se mechanická energie zachovává, můžeme tedy psát:
\[ \begin{aligned} E_{\mathrm{k}A} &= E_\mathrm{pe} = E_{\mathrm{p}B}\\ \frac{1}{2}mv_A^2 &= E_\mathrm{pe} = mgh_B \end{aligned} \]Pro maximální dosaženou výšku tedy dostáváme:
\[h_B=\frac{v_A^2}{2g}=\frac{10^2}{2\cdot9{,}81}\ \mathrm{m} = 5{,}1\ \mathrm{m}\]A protože jeho těžiště již na začátku bylo ve výšce kolem 1,0 m nad zemí, maximální dosažená výška se tedy pohybuje kolem šesti metrů a my vidíme, že ji skokan může ovlivnit svou počáteční rychlostí.
Energie nabývají velmi různých hodnot. Dokážete vyjádřit, jak velká je jednotka 1 J? Pro lepší představu o jejich řádové velikosti se podívejte na následující tabulku.
Tabulka (přehled energií):
| děj | odpovídající energie (J) |
|---|---|
| erupce sopky (odhad) | 1018 |
| roční spotřeba elektrické energie v ČR | 1017 |
| spálení 1 litru benzínu | 107 |
| denní příjem lidského těla | 107 |
| nabitá baterie v mobilu | 104 |
| srdeční stah | 1 |
| otočení stránky knihy | 10−3 |
| bleší skok | 10−7 |
| porušení vazby v DNA | 10−20 |
Práce vykonaná nekonzervativní silou. Změna mechanické energie
Síly, které nejsou konzervativní, mění množství mechanické energie soustavy. Mohou způsobit buď pokles mechanické energie přeměnou na teplo, nebo naopak nárůst mechanické energie tím, že přemění práci svalů na kinetickou nebo polohovou energii. Častokrát dochází k oběma dějům současně.
Práce vykonaná nekonzervativními silami mění hodnotu mechanické energie soustavy.
\[W_{F\mathrm{n}}=\Delta E_\mathrm{m}\]Vyjděme ze vztahu mezi celkovou prací všech sil a změnou kinetické energie:
\[W_F=\Delta E_\mathrm{k}\]Celková práce je součet prací vykonaných konzervativními silami a vykonaných nekonzervativními silami.
\[W_{F\mathrm{n}}+W_{F\mathrm{k}}=\Delta E_\mathrm{k}\]Jelikož práce vykonaná konzervativními silami je rovna záporně vzaté změně polohové energie \(W_{F\mathrm{k}}=-\Delta E_\mathrm{p}\), můžeme napsat \(W_{F\mathrm{n}}-\Delta E_\mathrm{p}=\Delta E_\mathrm{k}\) nebo také
\[W_{F\mathrm{n}}=\Delta E_\mathrm{p}+\Delta E_\mathrm{k}=\Delta E_\mathrm{m}\]Jak uvidíte v následujících příkladech, díky uvedenému vztahu je možné řešit pomocí energie i úlohy, kde působí nekonzervativní síly a nelze přímo použít zákon zachování mechanické energie.
Zdroj
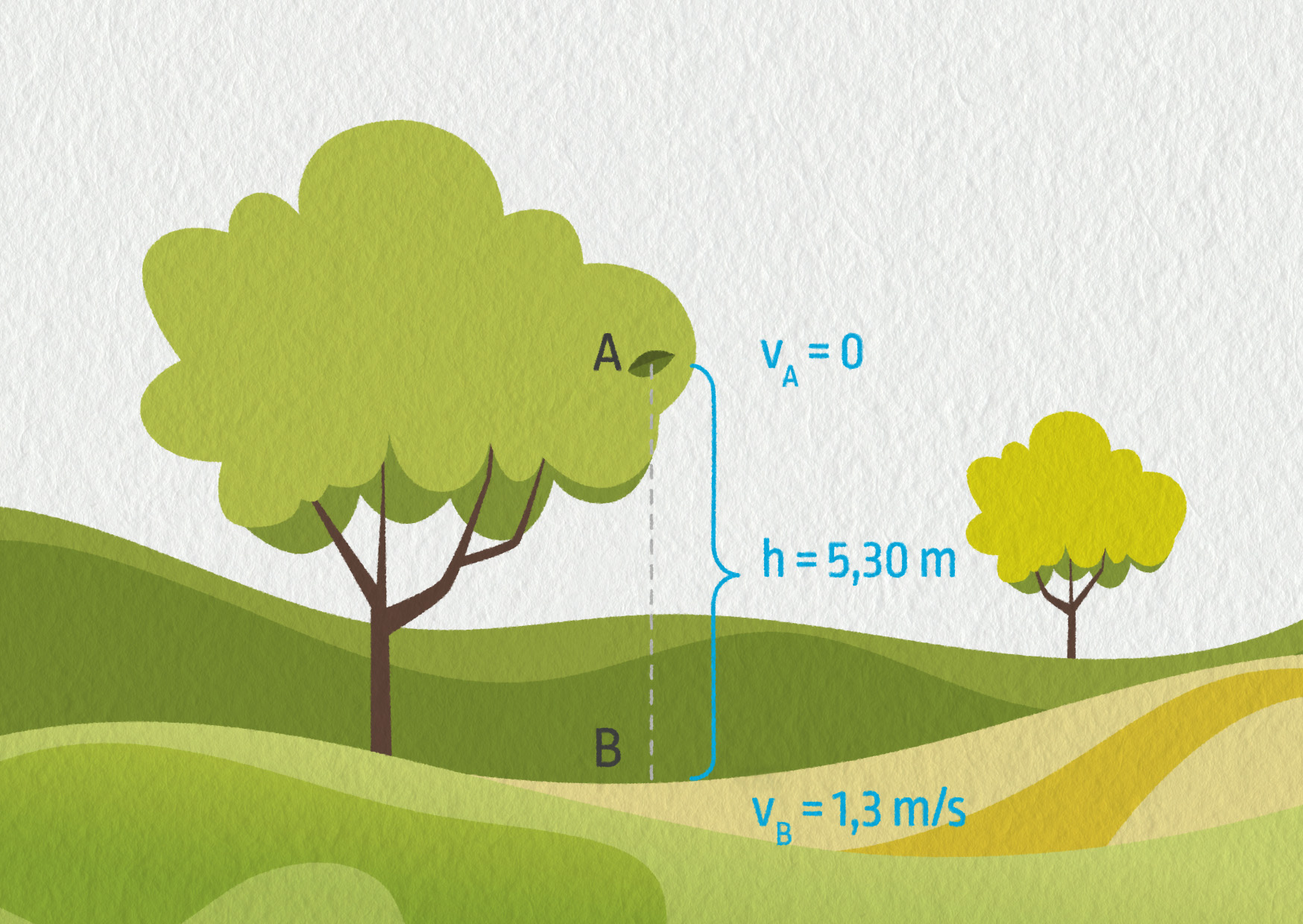
Musíme určit počáteční a konečnou hodnotu mechanické energie, neboť práce vykonaná nekonzervativními silami je rovna právě změně mechanické energie. Na začátku (bod A) má list nulovou rychlost, tím i nulovou kinetickou energii. Jeho potenciální energie je největší, protože je nejvýše nad zemí.
\[E_{\mathrm{k}A}=0\qquad E_{\mathrm{p}A}=mgh=0{,}017\cdot9{,}81\cdot5{,}30\ \mathrm{J}=0{,}884\ \mathrm{J}\]Při dopadu (bod B) je kinetická energie největší a polohová nulová, protože list dopadá na zem.
\[E_{\mathrm{k}B}=\frac{1}{2}mv_B^2=\frac{1}{2}\cdot0{,}017\cdot1{,}30^2\ \mathrm{J}=0{,}014\ \mathrm{J}\qquad E_{\mathrm{p}B}=0\]Změna mechanické energie je tedy rovna
\[\Delta E_\mathrm{m}=E_{\mathrm{m}B}-E_{\mathrm{m}A}=(0+0{,}014 + 0)-(0{,}884+0)\ \mathrm{J}=-0{,}870\ \mathrm{J}\]Takto velká je změna mechanické energie listu a tato energie se přeměňuje na energii, která způsobí pohyb (víření) vzduchu a na vnitřní energii listu a okolního vzduchu (díky čemuž se velmi mírně zahřejí).
Opět musíme rozlišit počáteční a konečný stav tělesa, tedy míčku. Vypočítáme jeho mechanickou energii. Na začátku pohybu, v bodě A, má největší kinetickou energii o velikosti \(E_{\mathrm{k}A}=\frac{1}{2}mv_A^2\). Na konci, má-li míček skončit v jamce (bod B), může mít nulovou rychlost, protože už jen spadne do jamky. Změna polohové energie nás nezajímá, míček se pohybuje po vodorovném greenu.
Změna mechanické energie je rovna práci nekonzervativních sil, tedy práci třecí síly míčku o green. Můžeme psát:
\[\Delta E_\mathrm{m}=E_{\mathrm{m}B}-E_{\mathrm{m}A}=0-\frac{1}{2}mv_A^2=W_{\Vec{F}_\mathrm{t}}=-F_\mathrm{t}\cdot4d\]Úbytek mechanické energie je tedy 4× větší než při prvním pokusu, nová rychlost tedy musí být 2× větší než původní, neboť kinetická energie je úměrná druhé mocnině rychlosti.
\[v_A=2\sqrt{\frac{2F_\mathrm{t}d}{m}}=2v_0\]Postupem času lidé objevili další formy energie (tepelnou, elektrickou, jadernou…) a zjistili, že celkové množství energie se nemění při libovolných dějích. To vedlo k formulování jednoho z nejdůležitějších zákonů fyziky – zákona zachování celkové energie. Pokud by se vám podařilo najít děj, při kterém se energie nezachovává (tedy pouze vzniká či zaniká), pak máte dvě možnosti. Buď jste se spletli, nebo vás čeká Nobelova cena za fyziku.

