Magnetické pole přímého vodiče
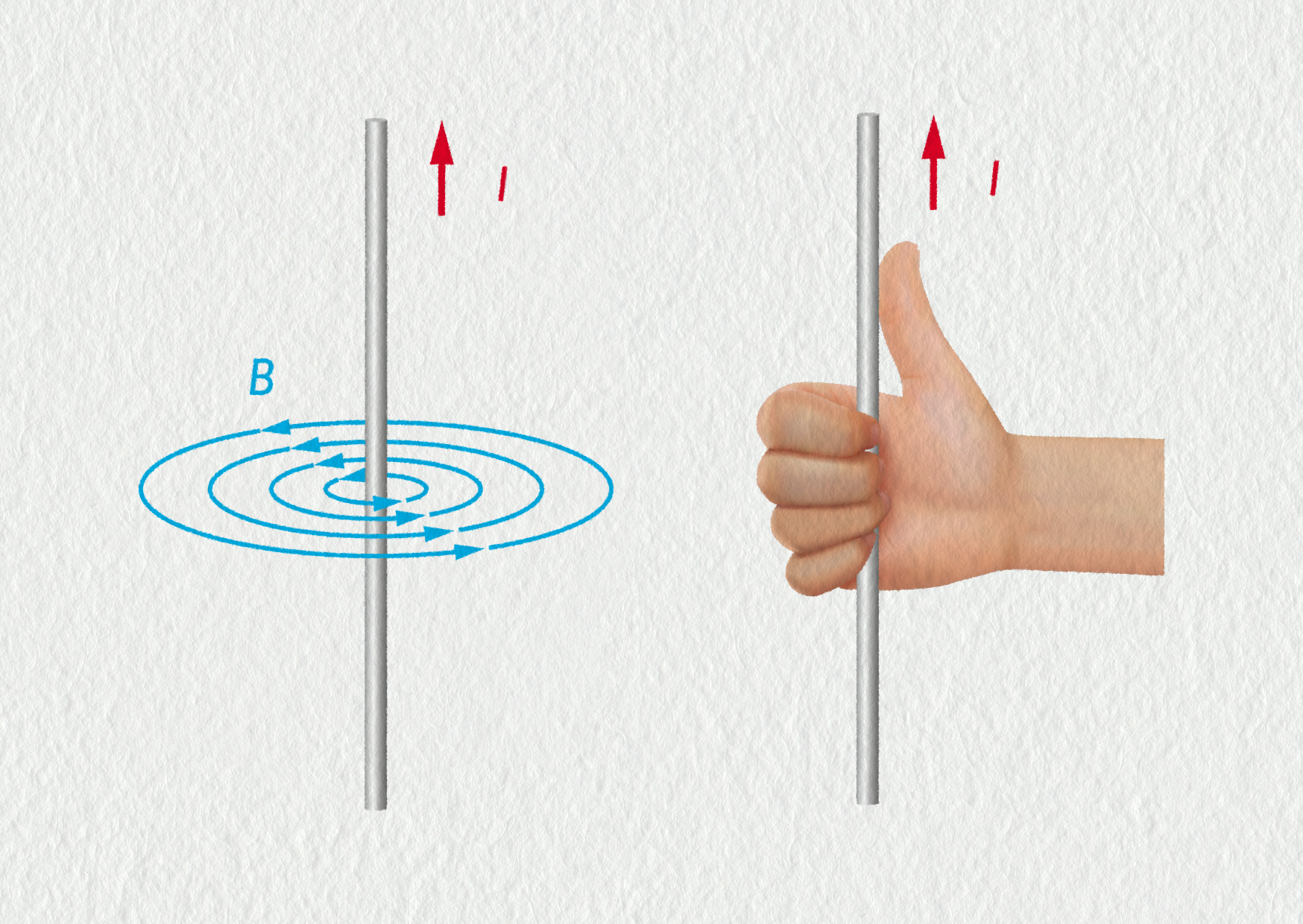
Pojďme nyní prozkoumat podrobněji magnetické pole vytvářené elektrickým proudem. Geometricky nejjednodušší je situace, kdy je vodič přímý a dlouhý. Pomocí železných pilin zjistíme, že magnetické indukční čáry mají tvar soustředných kružnic okolo vodiče (viz obrázek 19.17).

Zdroj
Pomocí kompasu je možné určit také jejich orientaci. Ta závisí na směru proudu a dá se snadno určit také teoreticky pomocí Ampérova pravidla pravé ruky. Pravidlo je znázorněno na ilustraci. Když přiložíme palec pravé ruky k vodiči ve směru proudu, pak prsty ukazují směr magnetické indukce.
Zdroj
Velikost magnetické indukce v některých jednoduchých situacích je možné odvodit teoreticky. V případě přímého vodiče dostaneme poměrně jednoduchý vztah
\[ B = \frac{\mu}{2\pi}\frac{I}{r} \]Velikost \(B\) je přímo úměrná proudu \(I\) ve vodiči a klesá se vzdáleností \(r\) od něj. Délka vodiče zde nehraje roli, neboť uvažujeme, že je dostatečně dlouhý vzhledem ke vzdálenosti \(r\), ve které indukci počítáme. Dál musí ve vztahu vystupovat konstanta, jejíž hodnotu je nutné určit experimentálně. Tato konstanta charakterizující prostředí okolo vodiče se nazývá permeabilita a značí se \(\mu\). S konstantou \(\mu\) zacházíme podobně jako s elektrickou permitivitou. Můžeme ji rozložit na součin permeability vakua \(\mu_0\) a relativní permeability prostředí \(\mu_\mathrm{R}\). Platí
\[ \mu = \mu_0 \mu_\mathrm{R}\;, \quad\hbox{kde}\quad \mu_0 = 1{,}257\cdot 10^{-6}\ \mathrm{T}\cdot\mathrm{m}\cdot\mathrm{A}^{-1}\;. \]Prakticky všechny látky vyjma feromagnetických mají relativní permeabilitu velmi blízkou jedné. Jejich přítomnost magnetické pole téměř neovlivňuje. U feromagnetik ale může relativní permeabilita dosahovat velmi vysokých hodnot. To je proto, že feromagnetika díky magnetickým doménám výrazně zesilují magnetické pole. Rekordmanem je slitina permalloy, kde hodnota \(\mu_\mathrm{R}\) může být řádově 100 000. Je to však materiál magneticky měkký, pro výrobu trvalých magnetů se proto nehodí. Vyrábí se z něj například jádra cívek.
Vypočítejte velikost magnetické indukce 1 cm od přímého vodiče, kterým teče proud 5 A. Výsledek porovnejte s tabulkou typických hodnot \(B\).
\[ B = \mu\frac{I}{2\pi r} = 0{,}0001\ \mathrm{T} = 0{,}1\ \mathrm{mT}\;. \]
Pole je slabší než u ledničkového magnetu, ale o něco silnější než magnetické pole Země, takže bychom ho dokázali zachytit pomocí magnetické střelky.
Z řešení příkladu vyplývá, že přímý vodič moc silné pole nevytvoří. Přesněji řečeno, byl by k tomu potřeba hodně velký elektrický proud. Na přímém vodiči je ale zajímavá ještě další věc – jeho magnetické pole nemá póly. Nabízí se tedy jedna praktická otázka. Jak vytvořit pomocí elektrického proudu silné magnetické pole a případně jak zařídit, aby vzniklo pole dipólové (se dvěma póly)? Odpovědí je cívka.
Magnetické pole cívky
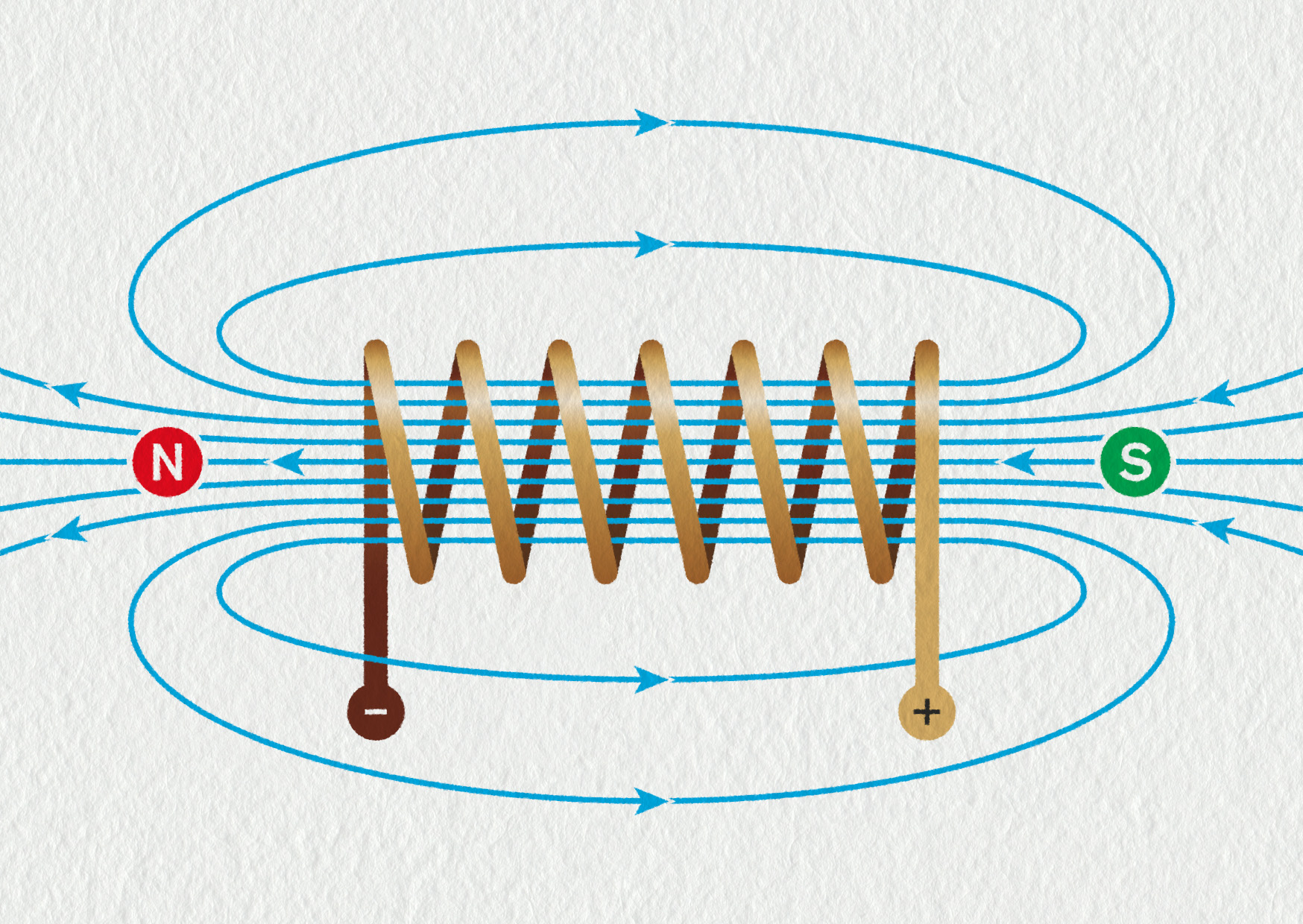
Cívka vznikne navinutím vodiče na nosnou kostru. Nejjednodušším typem cívky je solenoid – cívka tvaru válce (obrázek 19.19 vlevo). Další možností je toroid – cívka prstencového tvaru (obrázek 19.19 vpravo).

Zdroj
Přesnější představu o uspořádání indukčních čar solenoidu můžeme získat pomocí matematického modelu (viz obrázek vpravo). V těsné blízkosti vodičů vidíme kružnice stejně jako v případě přímého vodiče. Ve větších vzdálenostech se pole jednotlivých závitů sčítají a celkové magnetické pole cívky připomíná pole tyčového magnetu. Nejsilnější a přibližně homogenní je magnetické pole uvnitř solenoidu. Na obrázku vlevo je schematické znázornění stejné cívky včetně směru proudu a indukčních čar.

Zdroj
Směr vektoru \(\Vec{B}\) a s ním i směr indukčních čar určíme opět pomocí Ampérova pravidla pravé ruky. Použijeme ho pro libovolný kousek vodiče. Severní pól cívky je (stejně jako u magnetu) ten, ze kterého vycházejí indukční čáry směrem od cívky pryč. Pozor, kromě směru proudu zde hraje roli také směr navinutí cívky. Chce to trošku prostorové představivosti, jak si můžete vyzkoušet v kontrolní otázce.
Už jsme zmínili, že magnetické pole uvnitř solenoidu je přibližně homogenní. To platí jen v případě, kdy je cívka dostatečně dlouhá vzhledem ke svému průměru (lidově řečeno délka cívky je výrazně větší než průměr). Blízko okrajů cívky velikost \(\Vec{B}\) klesá. Pro magnetickou indukci uvnitř dlouhého solenoidu platí jednoduchý vztah
\[ B = \mu I\frac{N}{l}\;, \]kde I je velikost proudu, N je počet závitů a l je délka cívky.
- Vypočítejte velikost magnetické indukce uvnitř solenoidu o 400 závitech a délce 10 cm, kterým teče proud 5 A. Výsledek porovnejte s předchozím příkladem přímého vodiče.
- Navrhněte, jak dosáhnout uvnitř solenoidu co nejsilnějšího magnetického pole.
a) \(B=\mu IN/l=0{,}025\ \mathrm{T} = 25\ \mathrm{mT}\). Pole uvnitř cívky je 250krát silnější než 1 cm od přímého vodiče se stejným proudem.
b) Na první pohled se zdá odpověď jasná. Co nejvíc závitů na jednotku délky a zároveň co největší proud. Tyto dva požadavky jdou ale proti sobě. Požadavek na velký proud znamená, že musíme použít silnější vodič. Tenký vodič by měl moc velký odpor a cívka by se příliš zahřívala. Použitím silnějšího vodiče ale narazíme na to, že na jednotku délky nedokážeme navinout velký počet závitů. Je potřeba najít vhodný kompromis. V praxi je vždy důležité znát odpor cívky nebo maximální proud, který cívka vydrží.
Nakonec uvažme ještě možnost vložit do cívky feromagnetické jádro. Relativní permeabilita jádra může zvednout velikost \(B\) o několik řádů. Bude se ale jednat o magnetické pole uvnitř jádra, nikoliv ve vzduchu v jeho okolí.
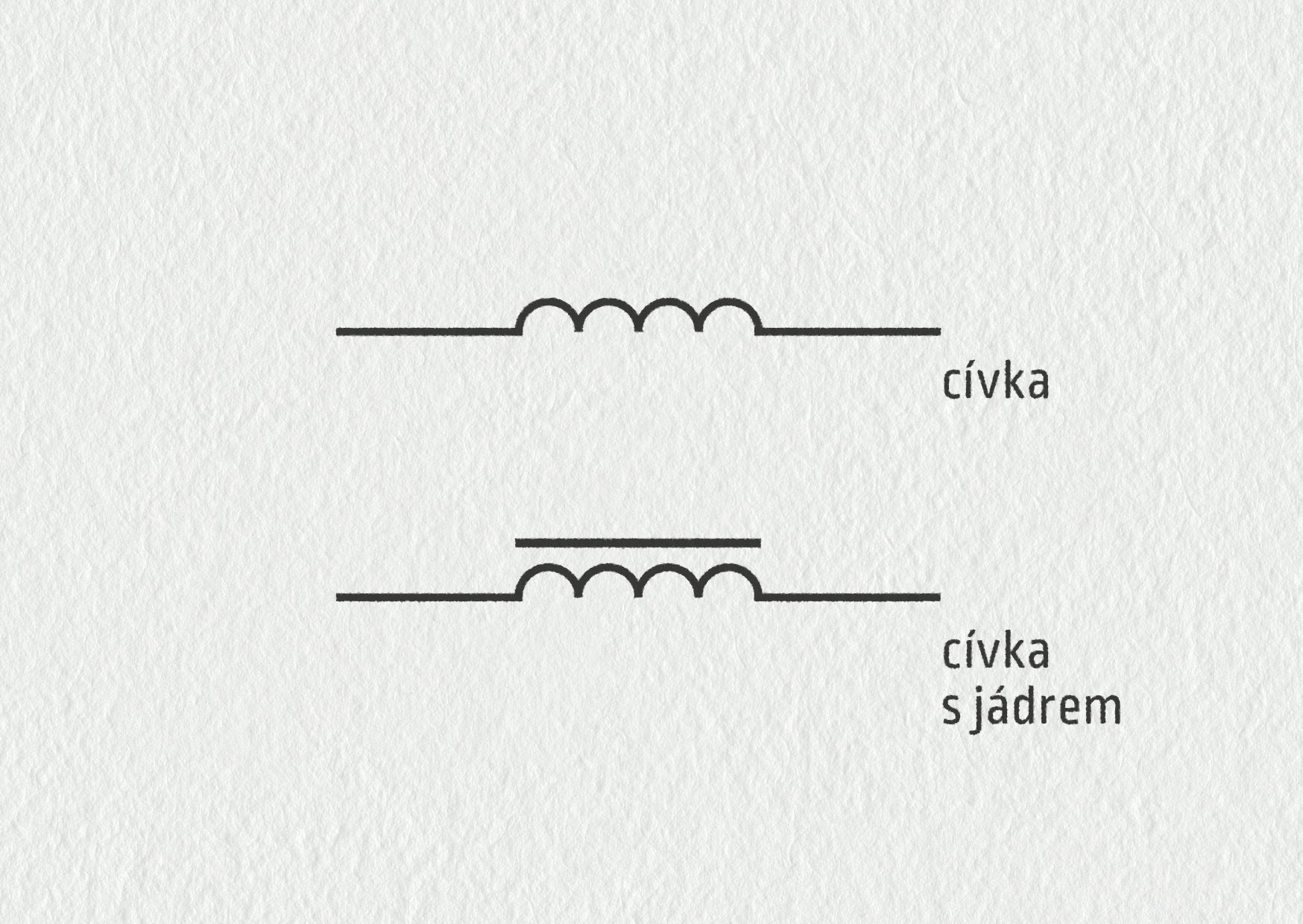
Ukázali jsme si, že cívku lze použít k vytvoření silného magnetického pole. To je možné uplatnit například v elektromagnetu. Tím ale význam cívek zdaleka nekončí. Jedná se o důležitou součástku v elektrotechnice, jejíž využití poznáte v kapitole 20. Cívka má také svou elektrotechnickou značku:
Zdroj

