Voltampérová charakteristika
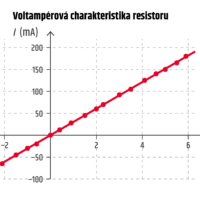
Proud a napětí jsou dvě základní veličiny elektřiny. Ukazuje se, že jejich souvislost je pro každou elektronickou součástku jiná a je třeba ji zjistit experimentálně. Vztah mezi napětím a proudem pro určitý spotřebič se nazývá voltampérová charakteristika, lze ji vyjádřit grafem nebo vzorcem.
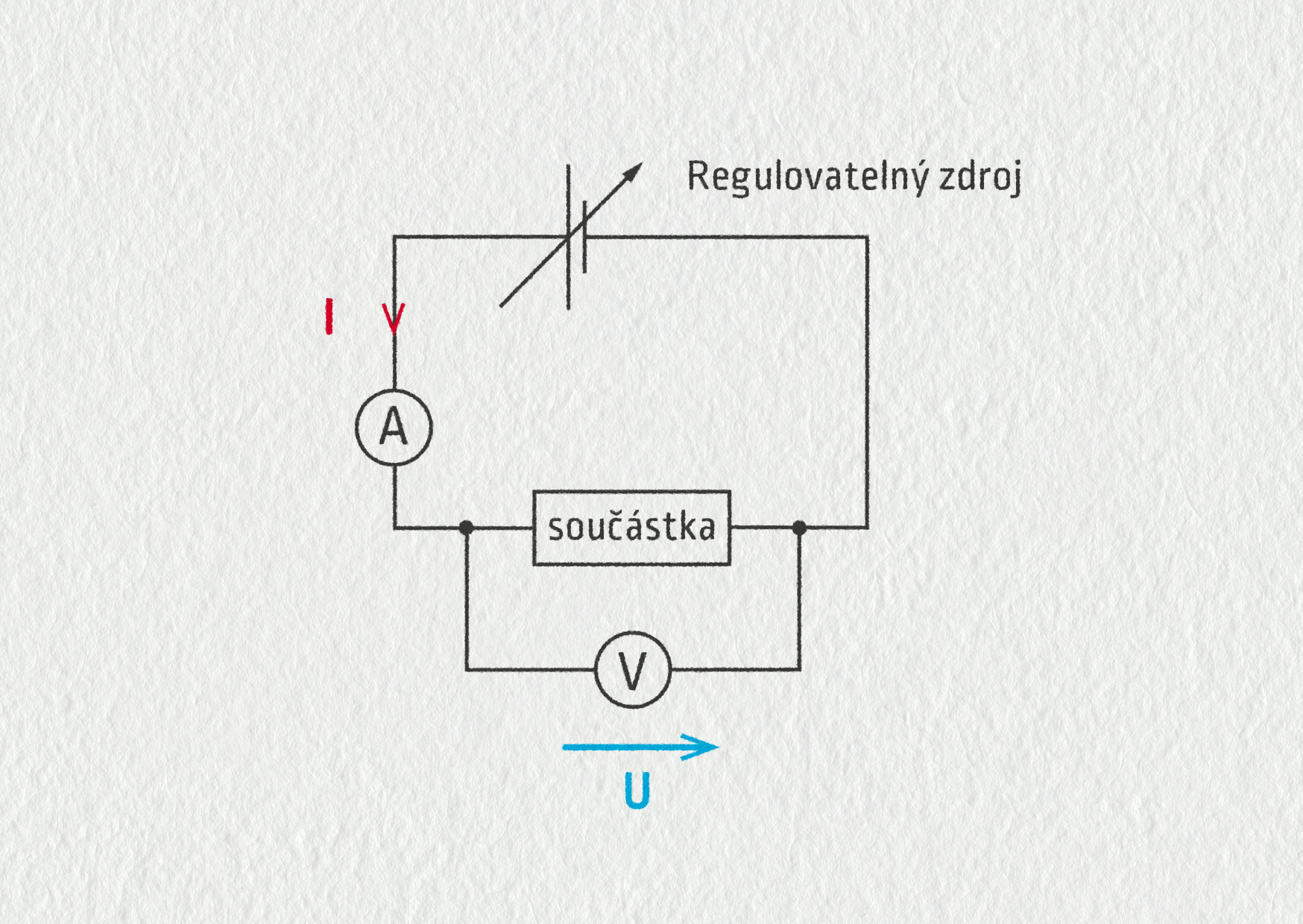
Zdroj
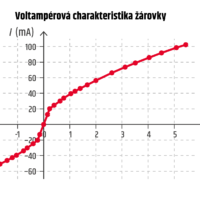
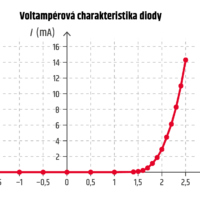
Předchozí grafy ukazují, že pro rezistor je proud přímo úměrný napětí, ale u jiných spotřebičů charakteristika tvar přímky nemá – je nelineární.
Přímá úměrnost \(I=kU\) platí pro všechny kovové vodiče o stálé teplotě. Dnes ji nejčastěji zapisujeme pomocí odporu \(R\), konstanta úměrnosti \(k\) ve vzorci má význam převrácené hodnoty odporu (\(k=1/R\)). To nám umožňuje formulovat následující experimentální zákon:
Ohmův zákon
Pro vodič o stálé teplotě je napětí mezi jeho svorkami přímo úměrné procházejícímu proudu.
\[U=RI\]Konstanta úměrnosti \(R\) se nazývá elektrický odpor.
Zákon je pojmenován po svém objeviteli, německém fyzikovi Georgu Simonu Ohmovi (1789–1854). Byl publikován v roce 1824 a je tak jednoduchý, že jej po několik desetiletí tehdejší vědci nebrali vážně.

Zdroj

Zdroj
Ohmův zákon nelze obecně používat pro polovodičové diody, pro kondenzátory, pro elektrochemické zdroje ani pro žárovku (viz níže).
Elektrický odpor a vodivost
Elektrický odpor je definován jako poměr napětí a proudu
\[R=\frac{U}{I}\]Jednotkou odporu je ohm
\[1\ \mathrm{\Omega}=\frac{1\ \mathrm{V}}{1\ \mathrm{A}}\]Elektrický odpor vyjadřuje, nakolik se součástka brání průchodu proudu: čím větší odpor, tím menší proud, a to při stejném napětí. Elektrický odpor je základní charakteristikou součástky nazývané rezistor, s jejímž fungováním jsme se seznámili na začátku této kapitoly.
Zatímco obsahem Ohmova zákona je přímá úměrnost mezi proudem a napětím, definici odporu můžeme použít i v případě, že si U a I nebudou úměrné – v tomto případě ovšem nebude vycházet R konstantní.
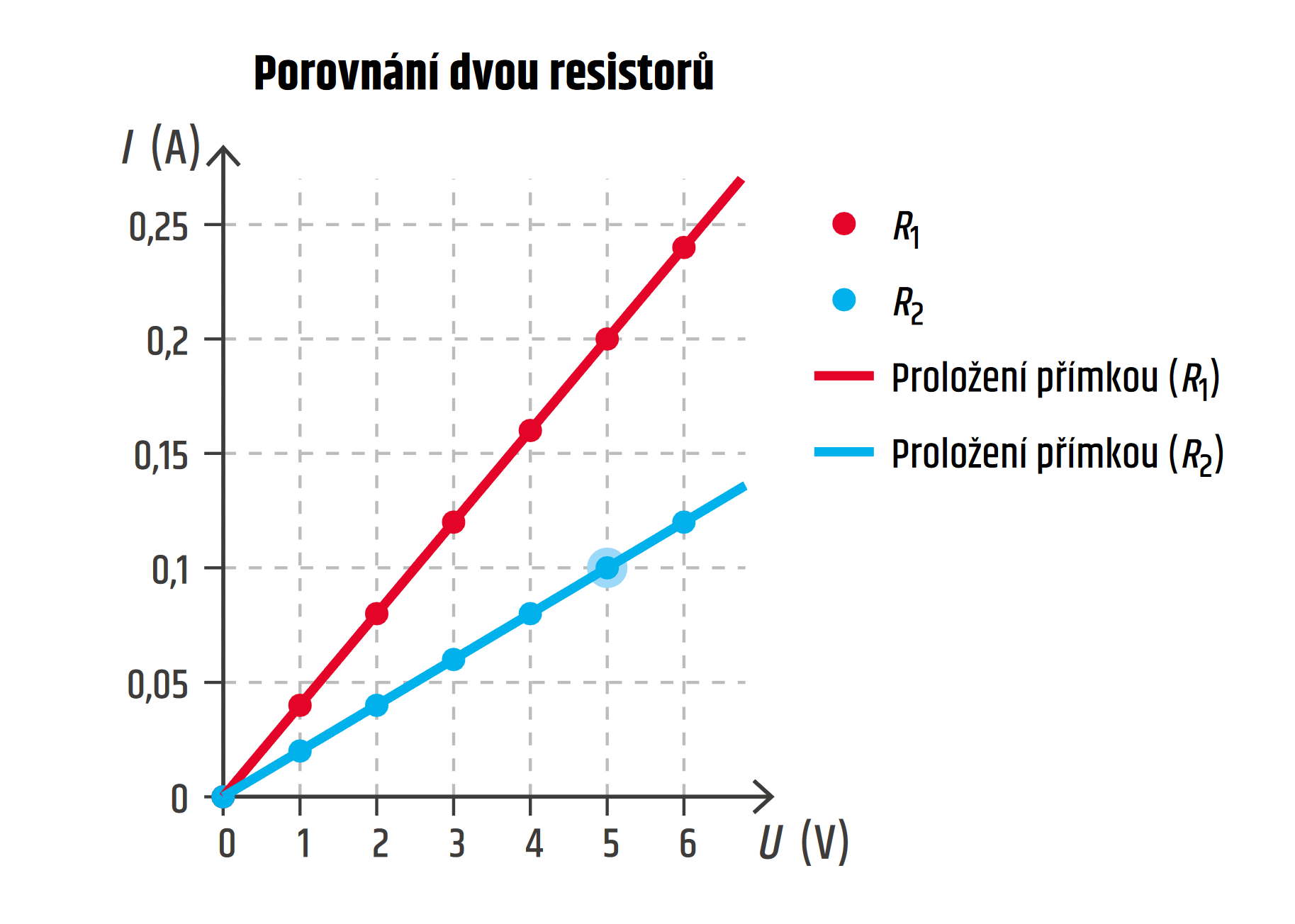
Graf znázorňuje voltampérovou charakteristiku dvou rezistorů.
Zdroj
- Který z rezistorů má větší odpor?
- Jaký je odpor rezistoru \(R_2\)?
a) Platí \(I=U/R\) čili čím větší odpor, tím menší proud (při stejném napětí). V grafu vidíme, že při určitém napětí, například 4 V, teče rezistorem \(R_1\) větší proud (0,16 A) než rezistorem \(R_2\) (proud 0,8 A). Rezistor \(R_2\) má tedy větší odpor.
b) V grafu si vybereme hodnoty, které lze snadno vydělit z hlavy. Rezistorem \(R_2\) protéká při napětí 5 V proud 0,1 A, takže
\[R=\frac{U}{I}=\frac{5\ \mathrm{V}}{0{,}1\ \mathrm{A}}=50\ \mathrm{\Omega}\]Převrácenou hodnotou odporu je elektrická vodivost \(G=1/R\), jednotkou vodivosti je siemens S.
\[[ G ]=\mathrm{S}=\frac{1}{\mathrm{\Omega}}=\frac{\mathrm{A}}{\mathrm{V}}\]Jednotka vodivosti siemens je pojmenována po německém vynálezci a podnikateli Werneru von Siemensovi (1816–1892). Siemens sestrojil dynamo, byl průkopníkem telegrafu a zakladatelem firmy nesoucí dnes jméno Siemens AG.

Zdroj
Jak závisí odpor na rozměrech vodiče?
Velikost, tvar a materiál vodiče ovlivňují jeho odpor.
Zdroj
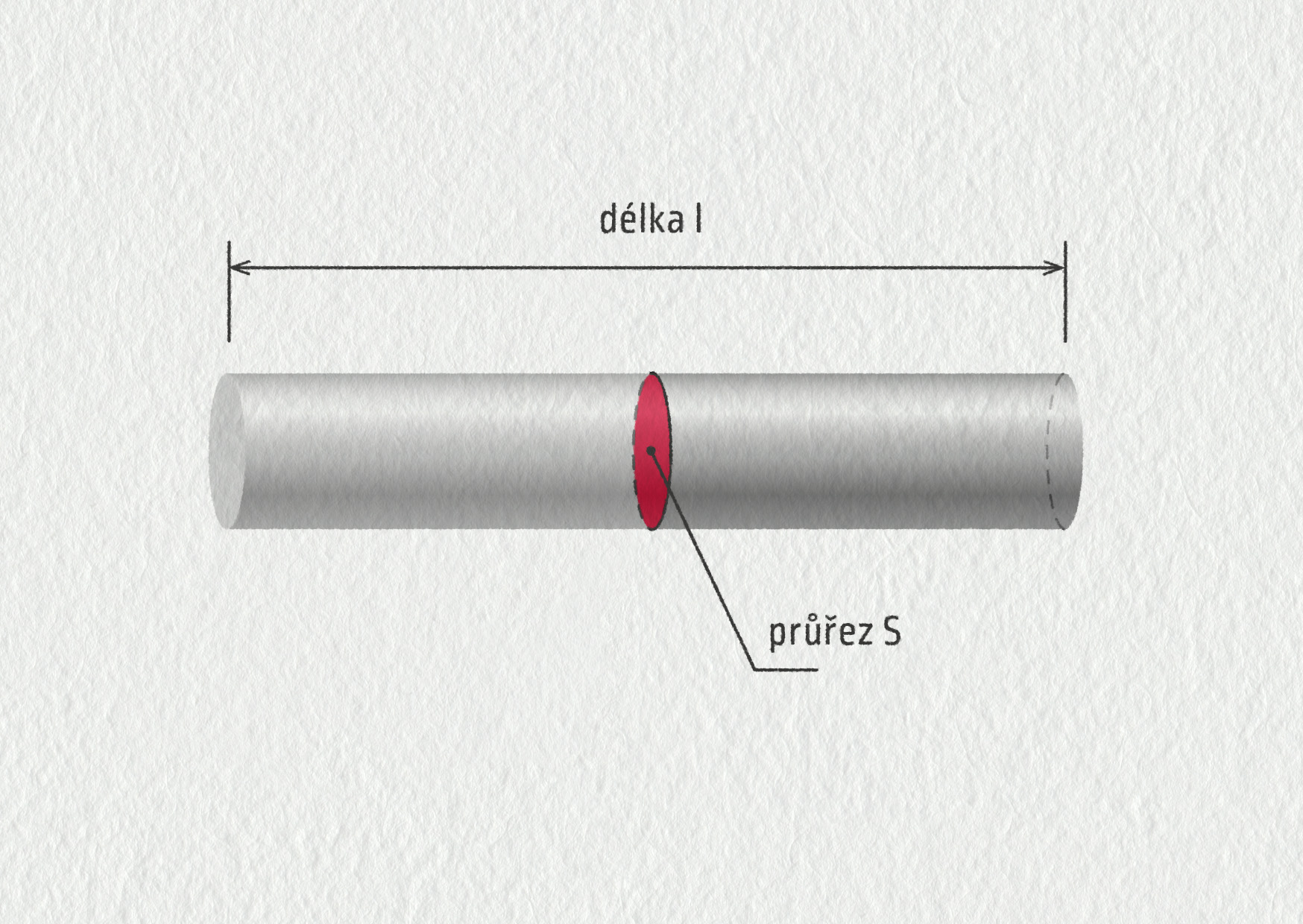
Odpor je přímo úměrný délce vodiče a nepřímo úměrný jeho průřezu. Nejjednodušeji to vyjádříme vzorcem
\[R=\varrho\frac{l}{S}\]kde R označuje odpor vodiče v Ω, l je délka vodiče v m, S je průřez vodiče v m2, ϱ je měrný odpor materiálu, z něhož je vodič vyroben. Měrný odpor (nazývaný též rezistivita) má jednotku Ω ⋅ m. Je to materiálová konstanta.
| kov | měrný odpor při teplotě 300 K (Ω ⋅ m) |
|---|---|
| stříbro | 16 ⋅ 10−9 |
| měď | 17 ⋅ 10−9 |
| zlato | 22 ⋅ 10−9 |
| hliník | 28 ⋅ 10−9 |
| zinek | 61 ⋅ 10−9 |
| platina | 111 ⋅ 10−9 |
| železo | 100 ⋅ 10−9 |
| cín | 120 ⋅ 10−9 |
| olovo | 208 ⋅ 10−9 |
| konstantan | 500 ⋅ 10−9 |
| nekovový materiál | měrný odpor při teplotě 300 K (Ω ⋅ m) |
|---|---|
| uhlík | 40 ⋅ 10−6 |
| čistá voda | 1,8 ⋅ 105 |
| sklo | 1017 |
| vzduch | závisí na vlhkosti |
| polystyren | 1020 |
Přestože je nejvodivějším materiálem stříbro, z ekonomických důvodů se k výrobě elektroinstalačních vodičů používá měď. Vodiče domovních rozvodů mívají průřez 2,5 mm2 nebo 1,5 mm2, zvonkový drát 0,8 mm2.
Používané vodiče

Zdroj

Zdroj
V příkladech i při nakupování je třeba pozorně číst parametry vodičů (poznáme podle jednotky):
Průměr \(d=2r\) neboli tloušťka drátu je dvojnásobek poloměru, udává se nejčastěji v mm.
Průřez \(S\) je plocha příčného řezu, pro vodič kruhového průřezu \(S=\pi r^2\), udává se v mm2.
Měrný odpor \(\varrho\) je materiálová konstanta nezávislá na tvaru a velikosti, najdeme v tabulkách, udává se v Ω ⋅ m (ohm krát metr).
Odpor na metr délky je komerční parametr, závisí na materiálu a průřezu drátu, udává se v Ω/m (ohm na metr).
Jak vzniká v látce odpor?
Kovový materiál vzniká z původně neutrálních atomů. Jakmile se k sobě atomy dostatečně přiblíží, začnou tvořit krystalovou mřížku a každý z atomů uvolní jeden, maximálně dva valenční elektrony. Kovy jsou tedy tvořeny krystalovou mřížkou složenou z kladných iontů a kolem nich se pohybují uvolněné, tzv. vodivostní elektrony.
Při pokojové teplotě se vodivostní elektrony pohybují neuspořádaně, podobně jako molekuly ve vzduchu, říkáme jim někdy „elektronový plyn“. Po připojení elektrického napětí se kromě chaotického „hemžení“ začnou kolektivně posouvat směrem ke kladnému pólu zdroje.

Zdroj
S mřížkovými ionty je to jinak: každý z nich je vázán ke svým sousedům a nemůže svoje místo opustit. To ovšem neznamená, že jsou v klidu. Všechny ionty kmitají kolem svých rovnovážných poloh.
Třebaže je krystalová mřížka pravidelná, vodivostní elektrony nemají pro svůj pohyb volnou (rovnou) cestu, srážejí se totiž s ionty, které se z rovnovážné polohy vychýlily. Odpor vzniká srážkami elektronů s nepravidelnostmi krystalové mřížky. Čím vyšší teplota a čím větší jsou výchylky iontů od pravidelné geometrické mřížky, tím větší překážku představují pro uspořádaný pohyb elektronů. Z toho nám logicky plyne teplotní závislost odporu.
Jak závisí odpor kovu na teplotě?
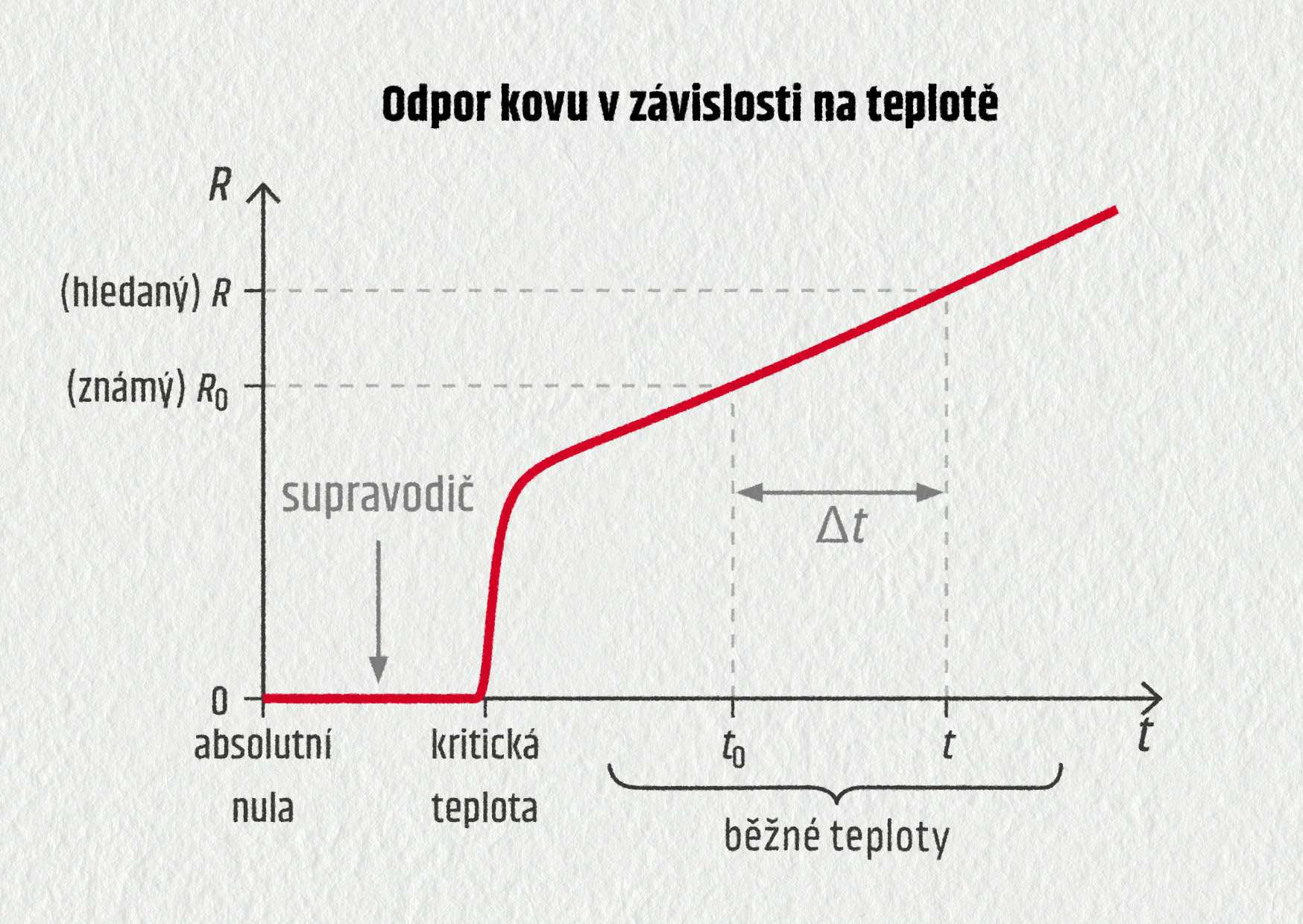
V širokém rozmezí teplot roste odpor téměř lineárně s teplotou.
Zdroj
Tuto závislost nejjednodušeji vyjádříme vzorcem
\[R=R_0(1+\alpha\cdot\Delta t),\]kde \(R\) označuje hledaný odpor při teplotě \(t\), \(R_0\) je známý odpor při (známé) referenční teplotě \(t_0,\) často bereme \(t_0=20\ ^\circ\mathrm{C}\), \(\Delta t=t-t_0\) je rozdíl teplot. Koeficient \(\alpha\) se nazývá teplotní součinitel odporu. Je to materiálová konstanta udávající, kolikrát se změní odpor při změně teploty o 1 °C. Její jednotkou je \(^\circ\mathrm{C}^{-1}\).
| kov | α (10−3 °C−1) |
|---|---|
| stříbro | 3,85 |
| měď | 3,93 |
| hliník | 4,03 |
| konstantan | 0,05 |
| železo | 6,5 |
| wolfram | 4,5 |
Zvláštní pozornost si zaslouží žárovka, jejíž vlákno je vyrobeno z wolframu (kov). S narůstajícím proudem se teplota vlákna zvyšuje, tím roste i jeho odpor. Při nestálém odporu už není proud přímo úměrný napětí, Ohmův zákon pro žárovku obecně neplatí – viz voltampérová charakteristika žárovky na obrázku 7.50b. Proudem se vlákno natolik zahřeje, že začne svítit.
Zajímavé je i chování některých kovů při velmi nízkých teplotách (teplotách blízkých absolutní nule, tj. −273,15 °C). Zchladíme-li čistý kov pod jistou kritickou teplotu (pro každý kov jiná), stává se z něj supravodič – jeho odpor poklesne přesně na nulu. V supravodivém prstenci může proud procházet libovolně dlouho, aniž by se odporem utlumil. Tento zvláštní stav hmoty se používá zejména v supravodivých cívkách k výrobě extrémně silných magnetických polí. V současnosti vědci usilovně hledají materiály, které by vykazovaly supravodivost i při běžných teplotách (vysokoteplotní supravodiče) – představa bezeztrátového přenosu elektrické energie je totiž ekonomicky velmi zajímavá.
Supravodivost objevil v roce 1911 Holanďan Heike Kamerlingh-Onnes (Nobelova cena 1913). S údivem zjistil, že při teplotě 4,2 K (přibližně −269 °C) padá odpor rtuti přesně na nulu!

Zdroj
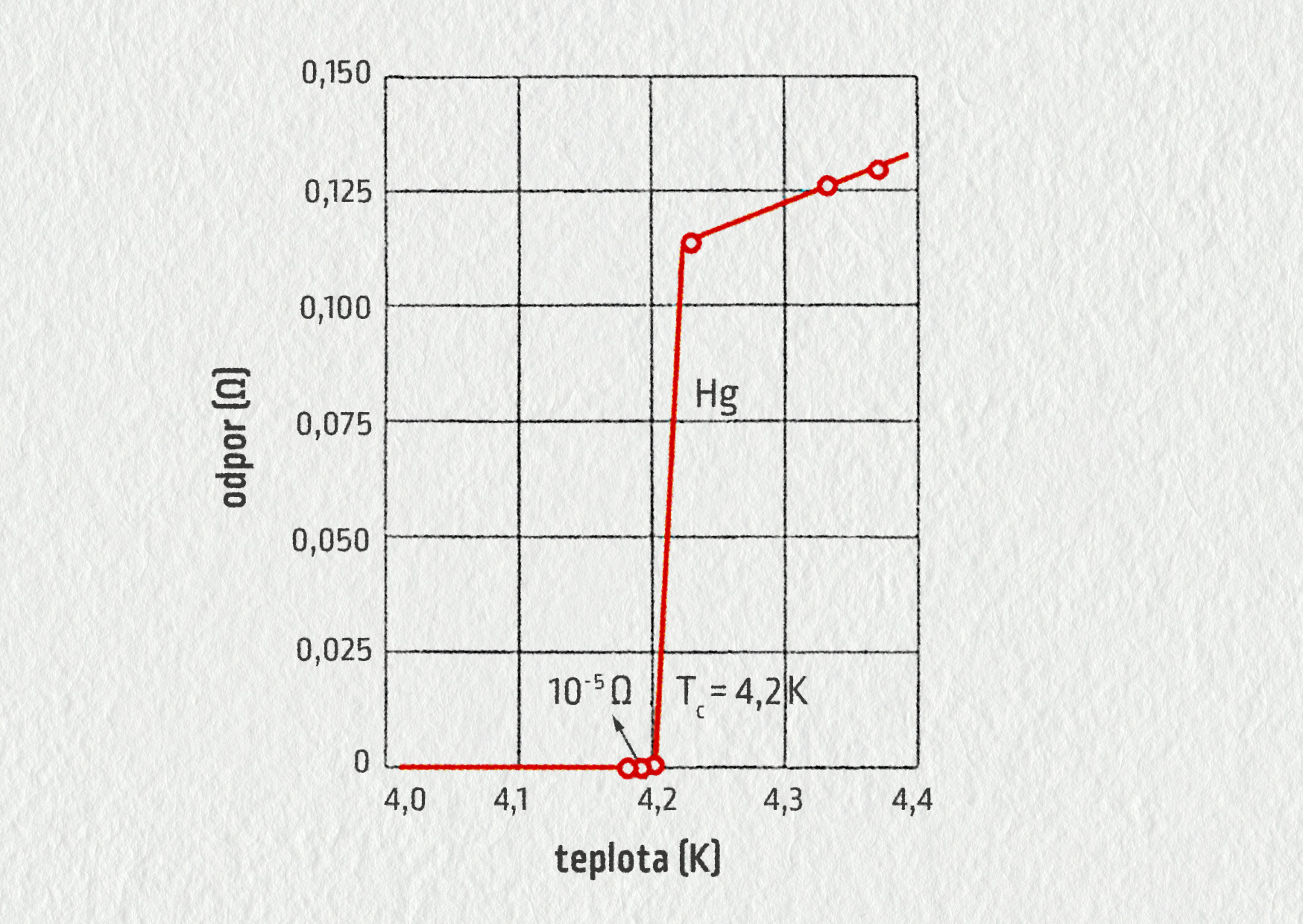
Zdroj
Pod kritickou teplotou jsou tepelné kmity mřížky natolik utlumeny a chaotický pohyb elektronů je natolik zpomalen, že se elektrony začnou kvantově „cítit“ a procházejí kovem synchronizovaně. To znamená, že v supravodivém stavu se neprodírá každý elektron mřížkou nezávisle na ostatních, ale naopak prochází materiálem koherentně s ostatními elektrony a synchronizovaně s kmity mřížky. Vysvětlení supravodivosti podali v roce 1957 Američané Bardeen, Cooper a Schrieffer – tzv. BCS teorie (Nobelova cena 1972).
Rezistor
Kromě vodičů na propojování součástek se z kovu vyrábějí rezistory. Rezistor je součástka s konstantní hodnotou odporu R. V běžném režimu svým odporem snižuje velikost proudu v určité větvi obvodu, a tím chrání jiné součástky před poškozením nadměrným proudem.
Zdroj
Dříve se rezistory vyráběly navinutím správné délky izolovaného drátu na nevodivý váleček. Dnes se na nevodivé keramické tělísko nejdříve nanese vrstva vodivého materiálu (kov nebo oxid kovu), pak se do ní vyfrézuje tenká spirálovitá drážka pro zvýšení odporu a celek se zataví do izolujícího pouzdra.
Používané rezistory

Zdroj
Zdroj

Zdroj

Zdroj

Zdroj
Hodnota odporu se na součástku vyznačí číslem (např. 330R = 330 Ω, 4k7 = 4,7 kΩ) nebo se použije barevný kód.

Zdroj