Co je podstatou elektrického proudu?
Vezměme malou žárovku a připojme ji ke zdroji. Kladný pól zdroje je místo s nedostatkem elektronů, na záporném pólu je elektronů přebytek. Vodivostní elektrony uvnitř vlákna žárovky jsou elektrickou silou přitahovány ke kladnému pólu a současně odpuzovány od záporného pólu zdroje a dají se kolektivně do pohybu ve směru působící elektrické síly. Vzniká elektrický proud.

Zdroj
Elektrický proud je uspořádaný pohyb nabitých částic.
Elektrický proud je fyzikální jev, při němž jsou všichni volní nositelé náboje téhož znaménka unášeni stejným směrem. Volným nositelem náboje je nabitá částice, která se může volně pohybovat. V kovech jsou to vodivostní elektrony a v kapalinách ionty. O existenci elektrického proudu se můžeme přesvědčit prostřednictvím jeho účinků.
Účinky elektrického proudu

Zdroj

Zdroj

Zdroj

Zdroj
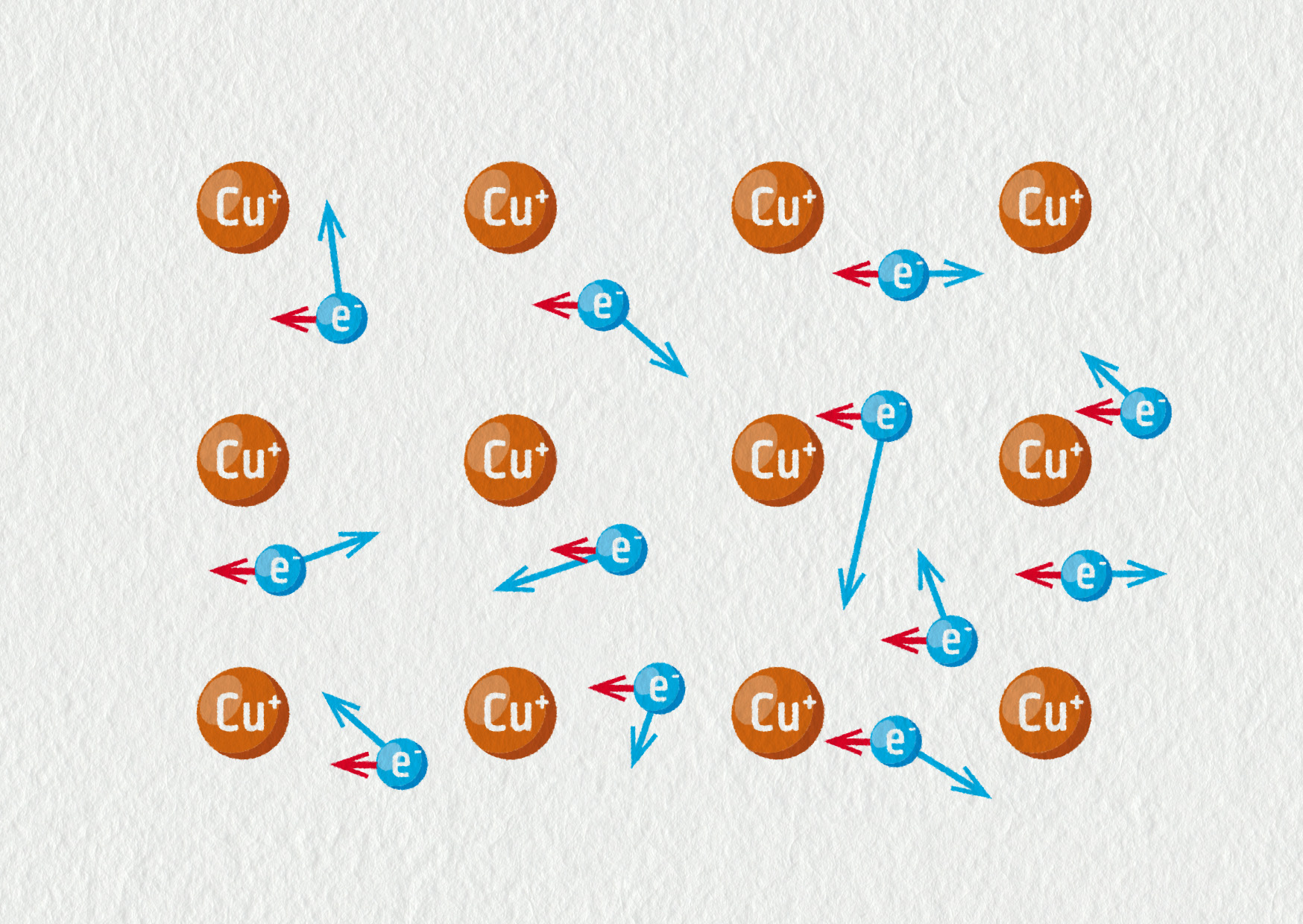
Při pokojové teplotě nejsou vodivostní elektrony uvnitř kovu v klidu, ale chaoticky se pohybují všemi směry podobně jako molekuly v plynu. Rychlost tohoto neuspořádaného pohybu je řádově 106 m/s. Po připojení zdroje tento pohyb pokračuje, ale elektrony se navíc začnou kolektivně posouvat ke kladnému pólu rychlostí řádově 1 mm/s = 10−3 m/s. Této rychlosti říkáme „driftová“ neboli „unášivá“ rychlost. Informace o připojení ke zdroji se kovem šíří rychlostí blízkou rychlosti světla ve vakuu, tj. 3 ⋅ 108 m/s.
Zdroj
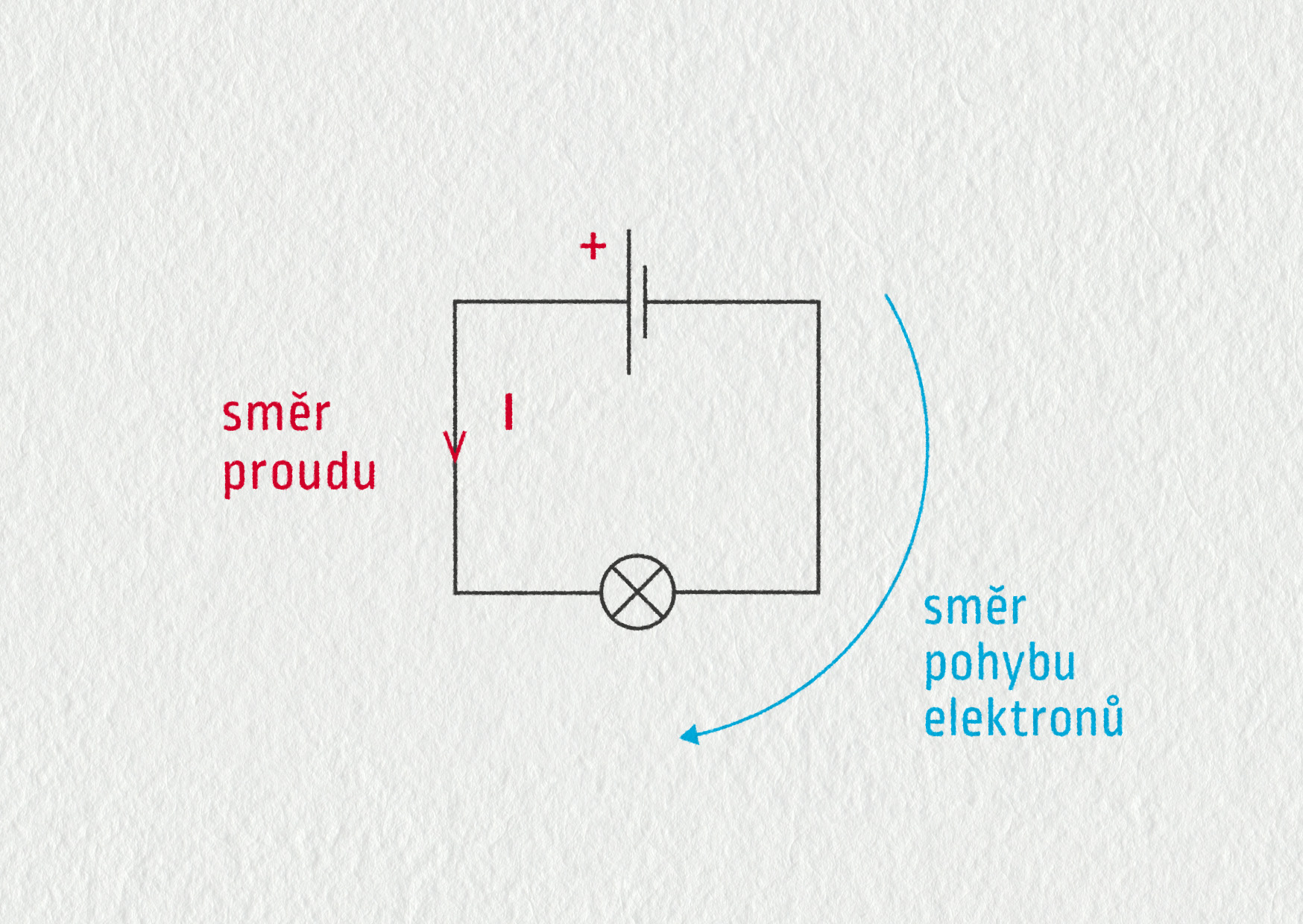
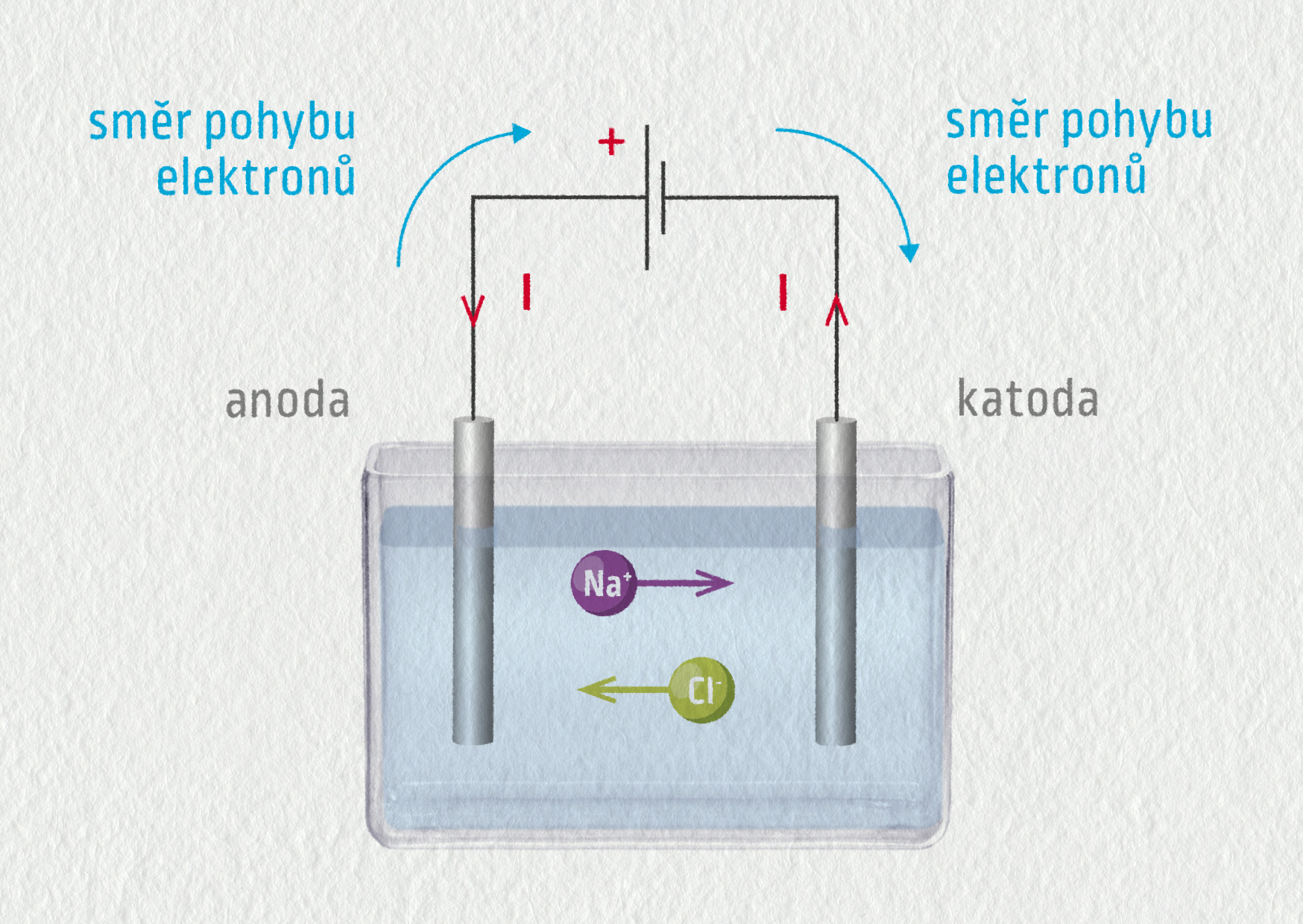
Příčinou elektrického proudu je elektrická síla vyvolaná vnějším zdrojem a působící na nositele náboje. Kladní nositelé (např. kladné ionty v kapalinách) se pohybují od + k −. Záporní nositelé (např. elektrony v kovech či záporné ionty v kapalinách) se pohybují opačným směrem, tedy od − k +, zcela v souladu s pravidly pro působení mezi náboji. Dohodou bylo stanoveno, že kladný směr proudu je směr kladných nositelů náboje.
Kladný směr proudu: od kladného k zápornému pólu zdroje.
Tato volba je poněkud nešťastná, protože elektrony se ve skutečnosti pohybují proti kladnému směru proudu. V době, kdy byl objeven elektrický proud (kolem roku 1800), neměli lidé ponětí o jeho podstatě. Věděli sice, že hýbe žabími stehýnky, „kope“ lidské tělo, ale netušili, co se děje na mikroskopické úrovni. Elektron byl objeven až o století později J. J. Thomsonem, v roce 1897.
Zdroj
Zdroj
Zdroj je příčinou elektrického proudu a současně určuje jeho směr v obvodu.
Pokud má zdroj kladný pól stále na stejném místě, jedná se o stejnosměrný zdroj a obvodem teče stejnosměrný proud. Jestliže se polarita svorek zdroje střídá, teče obvodem střídavý proud, směr proudu se trvale střídá.
Označení stejnosměrného proudu: ss, ⎓, DC (direct current).
Označení střídavého proudu: st, ∿, AC (alternating current).
K tomu, aby se v elektrickém obvodu objevil elektrický proud, musí být splněny dvě podmínky: obvod musí být uzavřen a musí obsahovat alespoň jeden zdroj.
Elektrický proud jakožto veličina
Elektrický proud I je fyzikální veličina vyjadřující množství náboje, které projde vodičem za časovou jednotku. Je základní veličinou v mezinárodní soustavě SI. Jednotkou elektrického proudu je ampér A. (1 A = 1 C/s).
Definice elektrického proudu
\(\displaystyle I=\frac{Q}{t}\)
- I … elektrický proud
- Q … celkový náboj, který vodičem projde
- t … doba, po kterou náboj vodičem prochází

Zdroj
Jednotka elektrického proudu je pojmenována po André-Marie Ampèrovi (1775–1836), francouzském fyzikovi proslulém díky objevům v elektrodynamice. Jeho jméno nese vztah pro magnetickou sílu působící na vodič s proudem v magnetickém poli, podepsán je pod vynálezem galvanometru a komutátoru.
V případě stejnosměrného proudu stálé velikosti projde za libovolně zvolený časový interval \(\Delta t\) vždy stejný náboj \(\Delta Q\), hodnota \(I\) se nemění. V opačném případě čili pokud množství náboje, který vodičem projde za časovou jednotku, kolísá, vztah \(I=\Delta Q/\Delta t\) definuje průměrný elektrický proud procházející po dobu \(\Delta t\).
Oproti tomu okamžitá velikost proudu, tj. hodnota \(I\) v určitém čase \(t\), je definována analogicky s tím rozdílem, že za \(\Delta t\) vezmeme libovolně (rozuměj nekonečně) malý časový interval, v němž leží okamžik \(t\), \(\Delta Q\) značí náboj prošlý během této (nekonečně) krátké doby \(\Delta t\). Okamžitá hodnota proudu v čase \(t\) se označuje malým i, tedy \(i=I(t)=\Delta Q/\Delta t\) pro \(\Delta t\) libovolně malé.
S použitím matematické symboliky
\[i=I(t)=\lim_{\Delta t\to0}\frac{\Delta Q}{\Delta t}=\frac{\mathrm{d}Q}{\mathrm{d}t}\;.\]Pokročilejší v matematice v tomto zápisu poznávají derivaci: okamžitá velikost proudu je derivací náboje podle času.
Jak se měří elektrický proud?
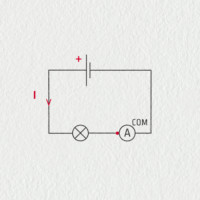
Elektrický proud se měří ampérmetrem, který je obvykle jednou z funkcí digitálního multimetru. Přestože některá nastavení provede ampérmetr automaticky, musíte pohlídat správnost zapojení a volbu veličiny nebo rozsahu. Klasický ampérmetr měří správně jen tehdy, pokud jím proud protéká, ampérmetr tedy zapojujeme do obvodu sériově.
Měření proudu
Zdroj
Zdroj

Zdroj
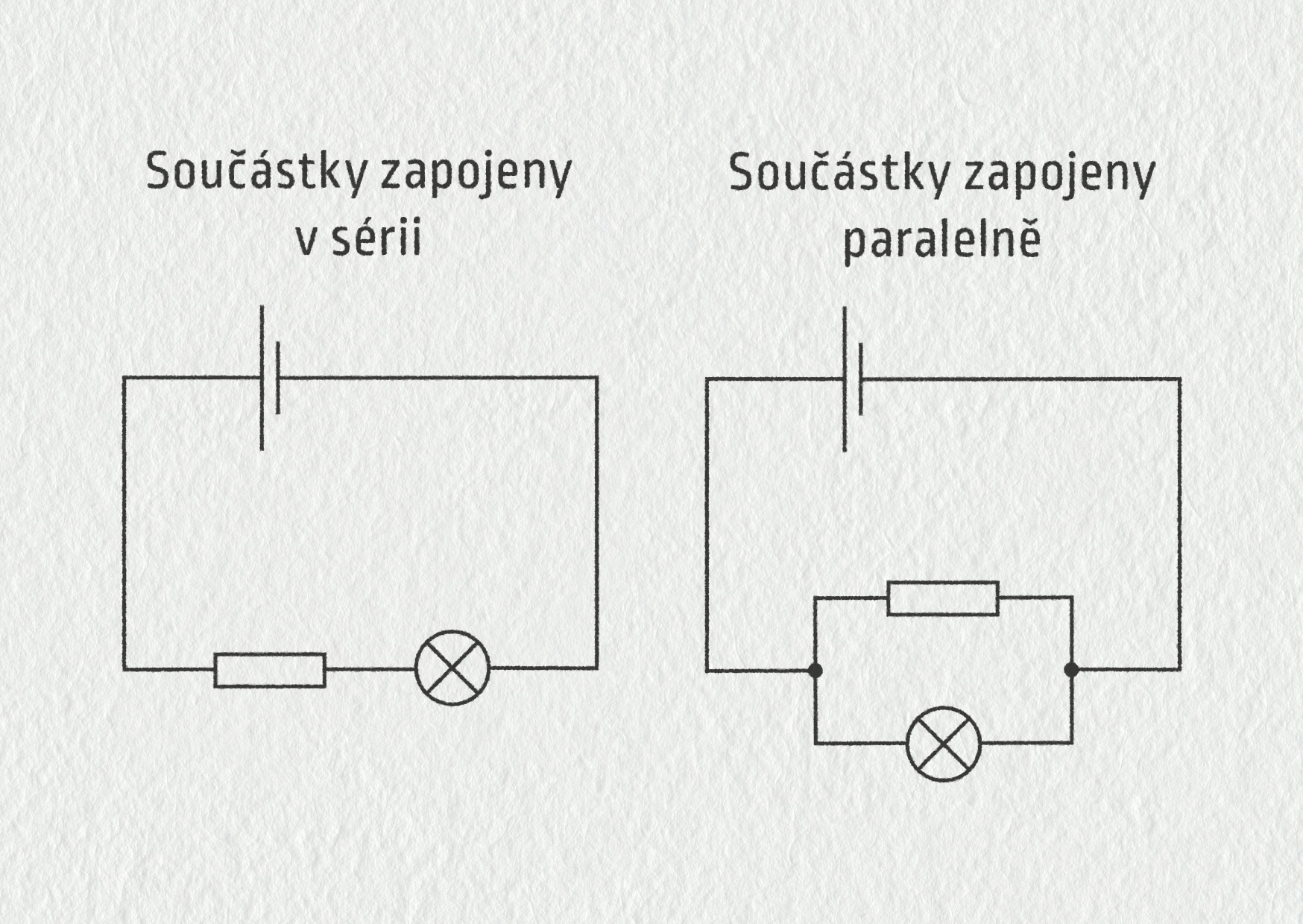
Sériové a paralelní zapojení znáte ze základní školy.
- Sériový obvod nemá žádná větvení, součástky jsou zapojeny za sebou podobně jako vagóny ve vlaku.
- Paralelní obvod obsahuje body větvení (uzly), součástky jsou zapojeny vedle sebe podobně, jako se drží tanečníci.
Obvody podrobněji rozebereme v 8. kapitole.
Zdroj
Rozsah ampérmetru je maximální hodnota proudu, jakou může ampérmetr měřit, aniž by byl poškozen. Měření začínáme vždy na největším dostupném rozsahu a pak dle potřeby měření zpřesňujeme postupnou volbou nižších rozsahů.

Zdroj
I při použití digitálního měřidla není nejistota (krajní chyba) měření proudu \(\Delta I\) nulová. Způsob výpočtu chyby je uveden v technické dokumentaci k ampérmetru a její hodnota je garantována výrobcem.
Zkoušeli jste někdy, nakolik je voda vodivá?
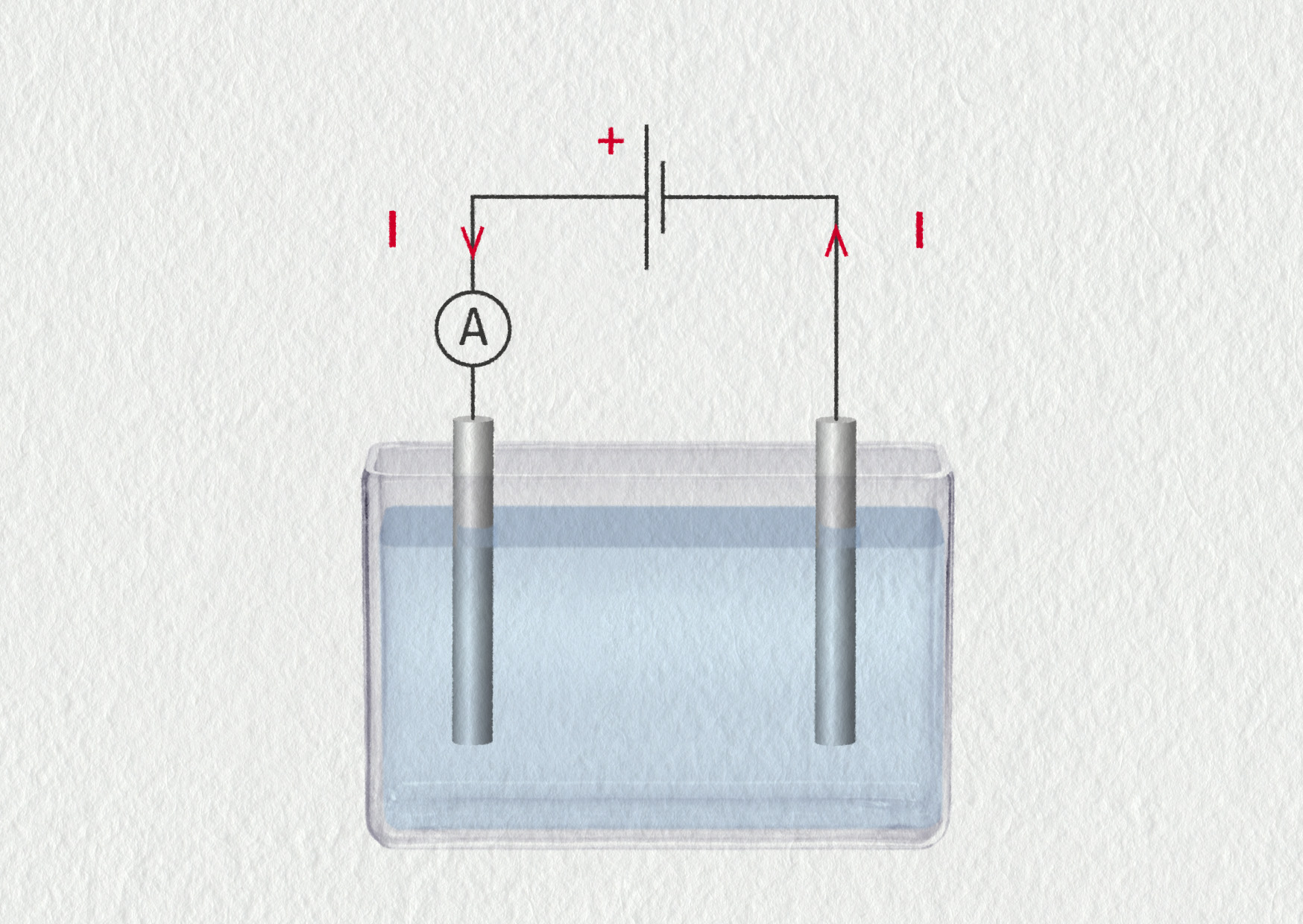
Budete potřebovat tužkovou baterii, dva plíšky ze stejného kovu (slouží jako elektrody), ampérmetr a vodiče. Připravte si tři stejné skleničky, naplňte je vodou z kohoutku, do druhé nasypte lžičku soli, do třetí dvě lžičky cukru a dobře promíchejte. Ponořte elektrody vždy ve stejné vzdálenosti do skleničky, zapojte sériový obvod s ampérmetrem a takto změřte elektrický proud ve všech třech kapalinách. Elektrody se nesmí vzájemně dotýkat a nesmí zůstat znečištěny předchozím roztokem.
Zdroj
- Proč je proud ve slané vodě největší?
- Proč čistá voda vede proud?
- Proč oslazená voda vede ještě méně než čistá?
- Slaná voda obsahuje nejvíce volných nositelů náboje. Jsou to ionty \(\mathrm{Na}^+\) a \(\mathrm{Cl}^-\), které vznikly disociací NaCl.
- Voda z kohoutku není chemicky čistá látka. Mezi neutrálními molekulami \(\mathrm{H_2O}\) je rozpuštěno mnoho minerálních látek v podobě iontů \(\mathrm{Ca}^{2+}\), \(\mathrm{Na}^+\), \(\mathrm{Mg}^{2+}\), \(\mathrm{Cl}^-\), \(\mathrm{HCO}_3^-\), \(\mathrm{OH}^-\), … I při použití destilované a deionizované vody byste naměřili nenulový proud, neboť molekuly \(\mathrm{H_2O}\) v malém množství spontánně disociují \(\mathrm{2H_2O\to H_3O^++OH^-}\), takže i chemicky čistá voda obsahuje oxoniové a hydroxidové ionty. Proto vždy, když hrozí nebezpečí úrazu elektrickým proudem, je voda vaším nepřítelem.
- Molekuly sacharózy \(\mathrm{C_{12}H_{22}O_{11}}\) ve vodě nedisociují na ionty. Jsou to relativně velké molekuly a pro pohyb ostatních iontů v kapalině představují překážku v pohybu.
Vlastnosti elektrického proudu
Poznatky zmíněné v tomto odstavci si můžete objevit samostatně během laboratorního cvičení Měření elektrického proudu. Jsou přímým důsledkem všeobecně platného zákona zachování náboje pro elektrické obvody.
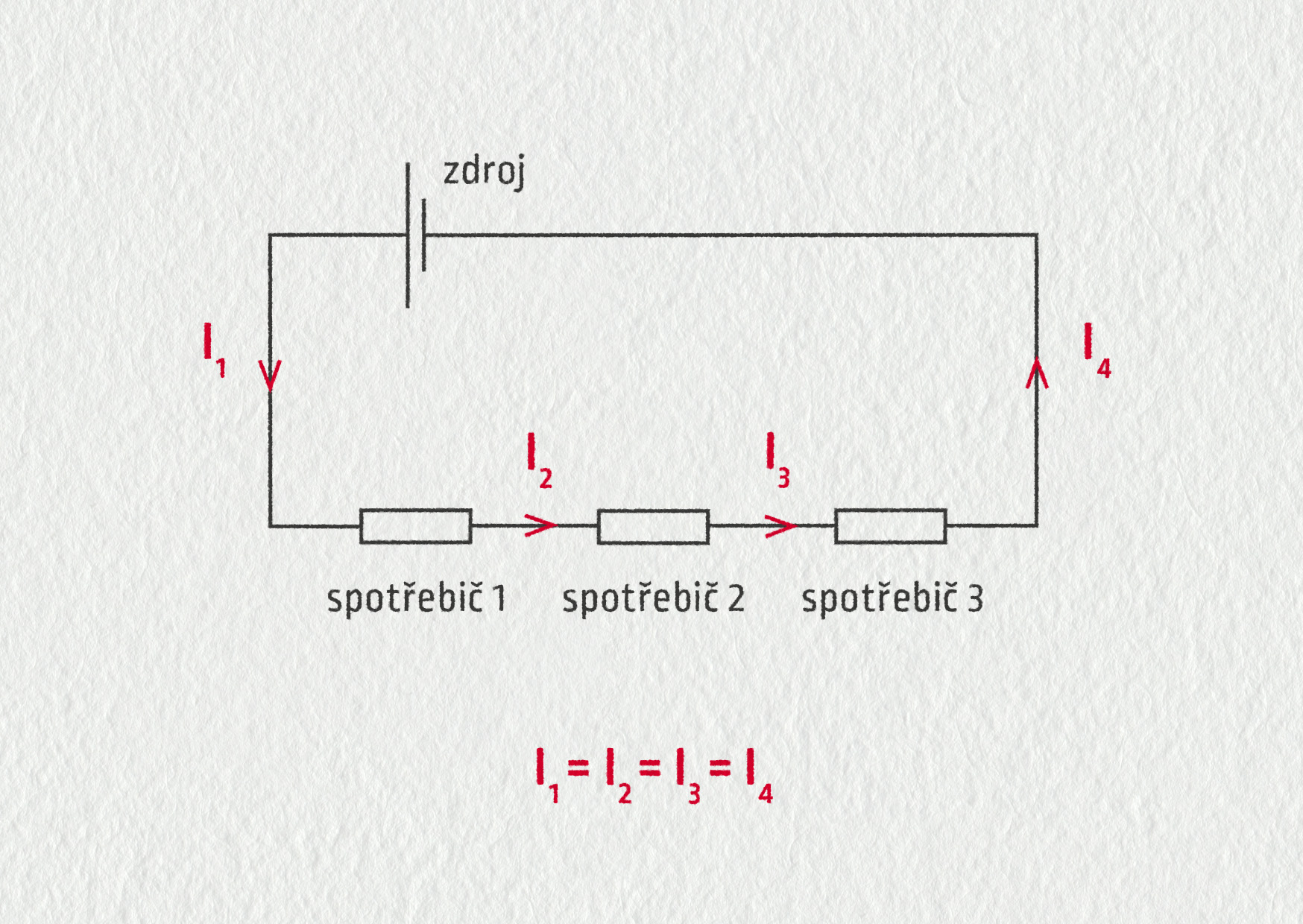
V sériovém obvodu má elektrický proud ve všech místech stejnou hodnotu.
Zdroj
Elektrický náboj nelze vytvořit ani zničit: náboj, který za sekundu do spotřebiče na jedné straně vteče, musí na druhé straně ze spotřebiče vytéct.
Součet proudů vtékajících do uzlu je roven součtu proudů z uzlu vytékajících:
\[\sum I_{\mathrm{do}}=\sum I_{\mathrm{ven}}\]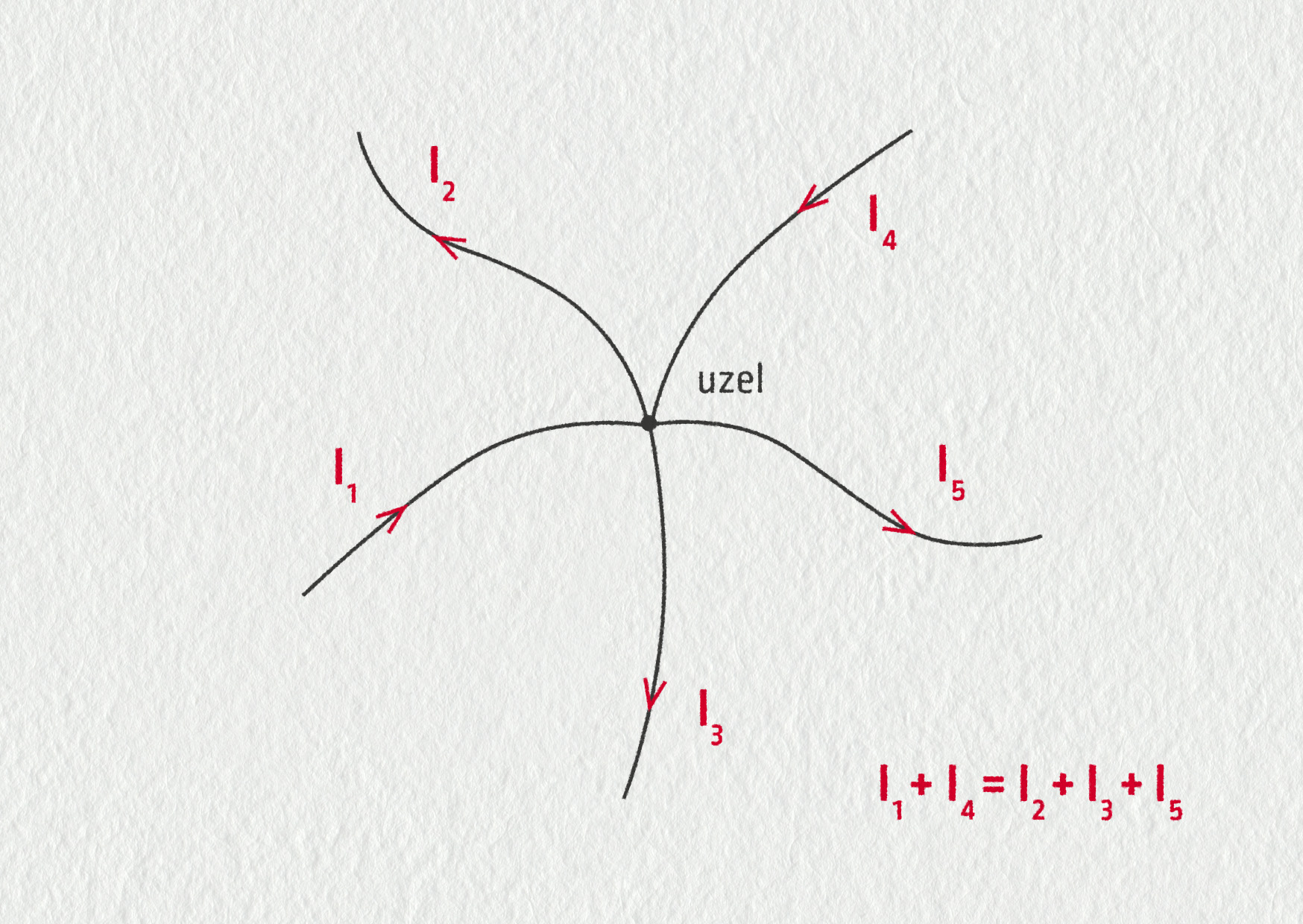
Zdroj
Uzel je místo (vodivého) spojení minimálně tří vodičů. V uzlu náboj nevzniká ani nezaniká, co za sekundu vteče dovnitř, musí vytéct i ven.
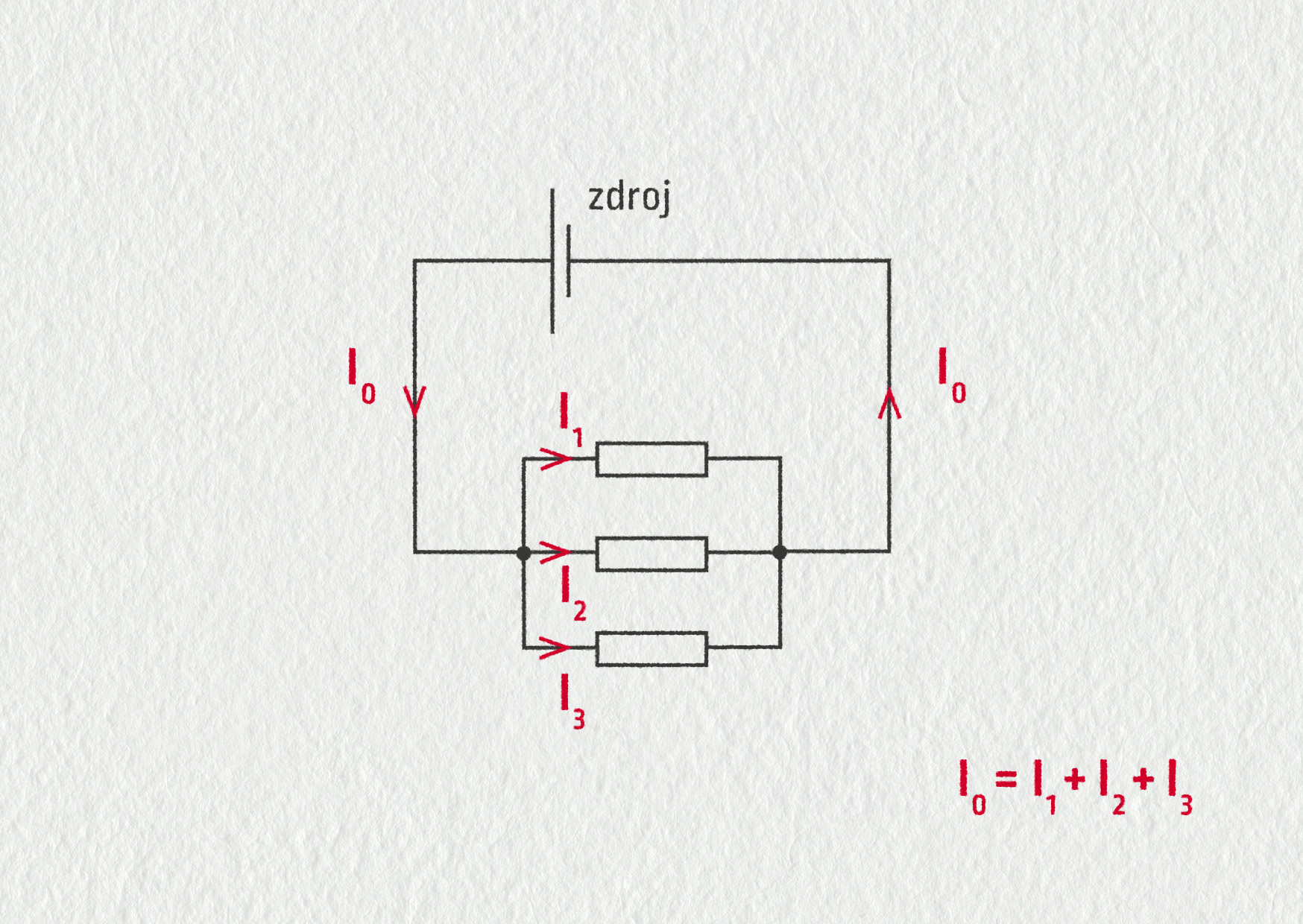
Zdroj
Proudění nábojů v obvodu můžeme přirovnat k proudění vody trubkami. Potom nás nepřekvapí, že ampérmetr (vodoměr) se musí zapojovat sériově, že v jednom vodiči (v jedné trubce) musí být průtok vždy stejný, nezávisle na tom, ve kterém místě proud měříme, a že v uzlu vodičů (rozvětvení trubek) musí platit výše uvedené tvrzení.
Vypočítejte proudy \(I_1\) a \(I_2\) tekoucí žárovkami.
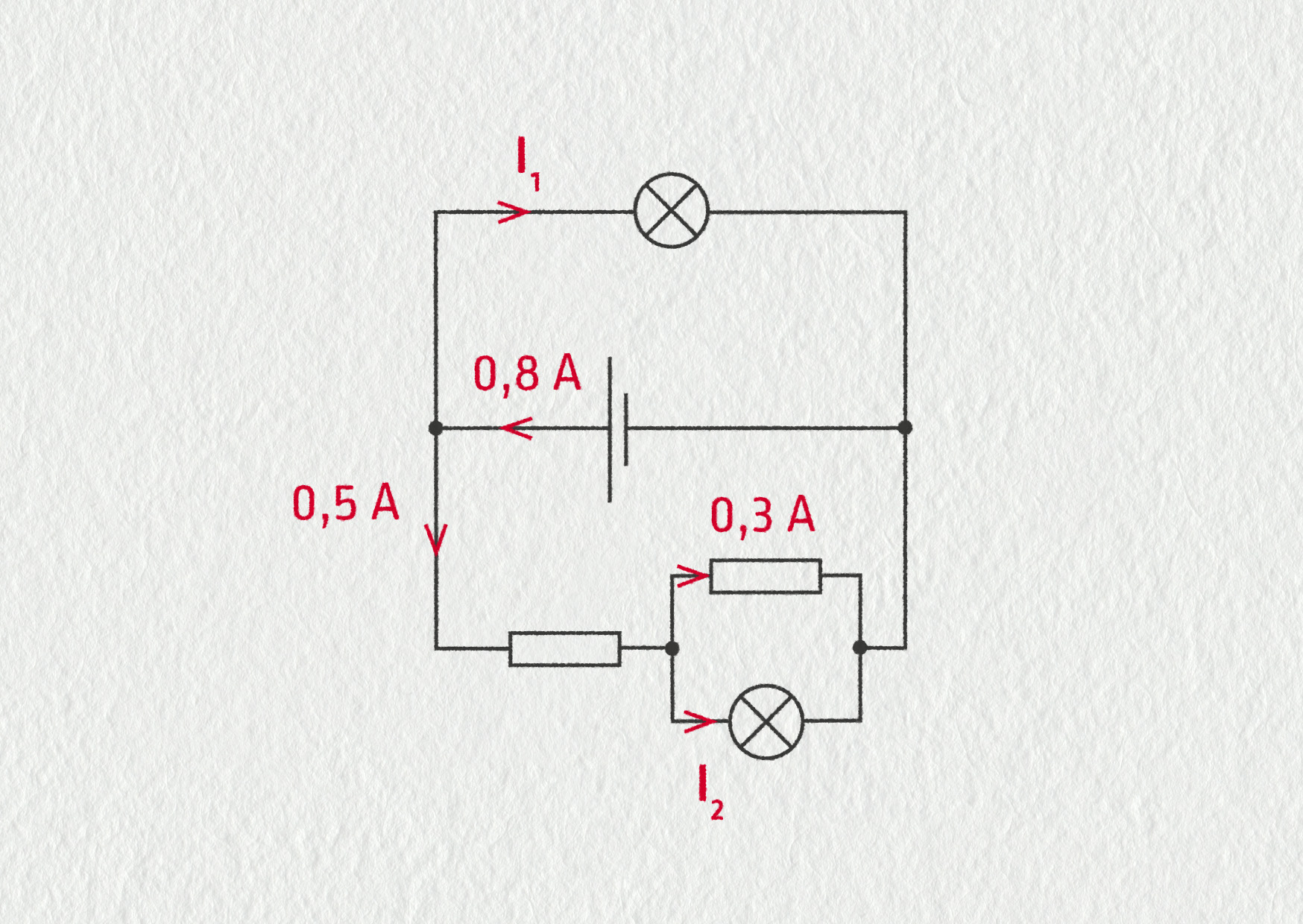
Zdroj
Zapište hodnotu proudu v ampérech (A).
\(I_1={}\)
\(I_2={}\)

