Gravitační pole

Co je to pole?

Každý člověk si dokáže představit, že tělesa, která se dotýkají, na sebe mohou působit silami. Jak je to ale s působením na dálku? Copak jedno těleso může prázdným prostorem na dálku ovlivňovat jiná tělesa?

Lidé postupně pochopili, že tělesa svojí přítomností ovlivňují vlastnosti okolního prostoru – vytvářejí kolem sebe pole. Hmotná tělesa (všechna) vytvářejí pole gravitační, elektricky nabitá tělesa vytvářejí pole elektrické. Pokud se do takového pole dostane jiné těleso, bude na ně působit síla. Říkáme, že pole má silové účinky. Obecně vzato je pole jedním z projevů hmoty, odlišné od látky, zprostředkovávající působení mezi tělesy.

Jak vypadá gravitační pole?

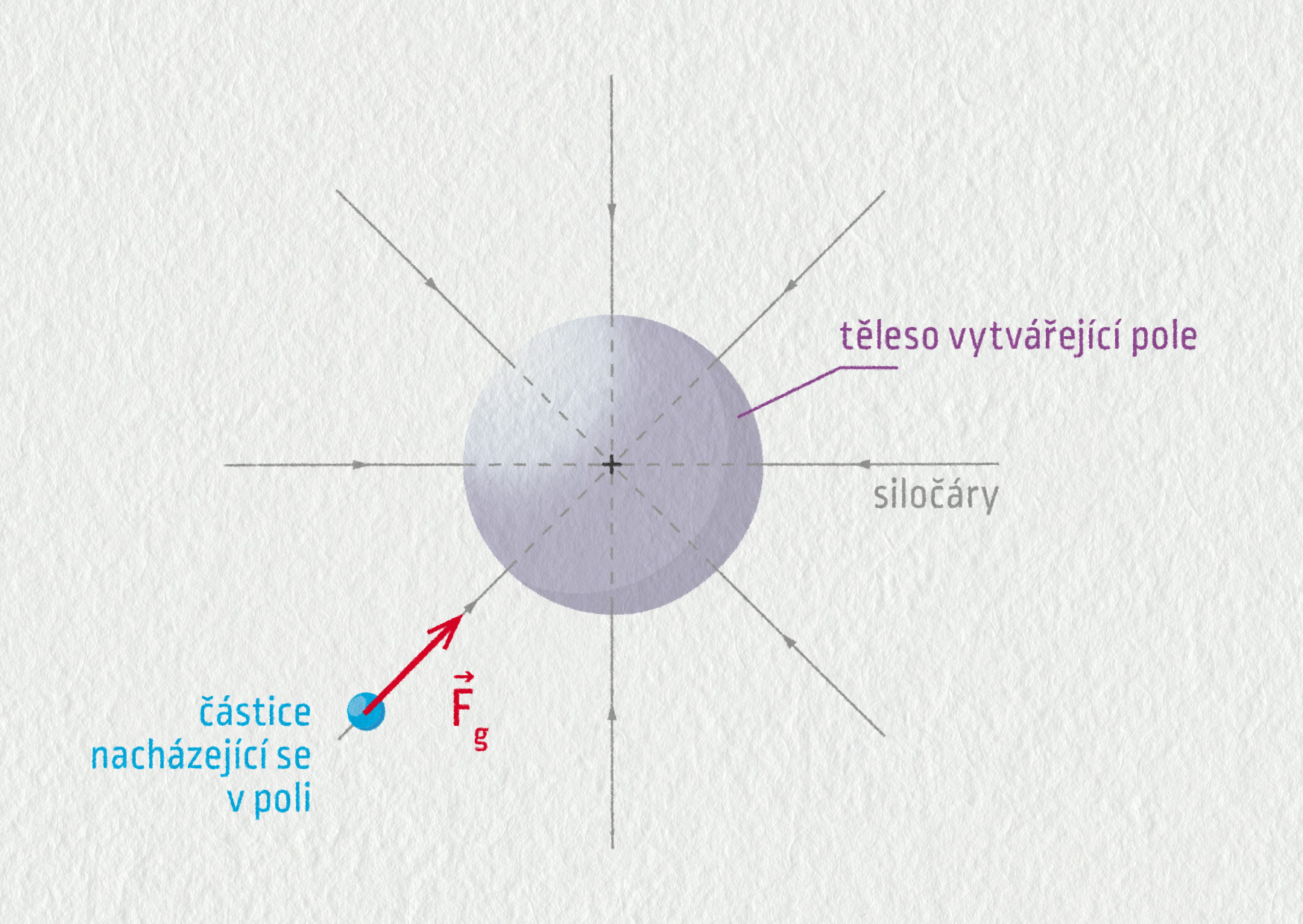
Existuje několik způsobů, jak si představit gravitační pole. Nejjednodušší způsob je znázornění pomocí siločar. Siločára je křivka, která v každém místě ukazuje směr gravitační síly. Přesněji řečeno, vektor \(\Vec{F}_\mathrm{g}\) má v každém místě směr tečny k siločáře – viz obrázek 17.23. Hustota siločar pak udává, jak je pole silné.

17.23 – Siločáry gravitačního pole.
Zdroj

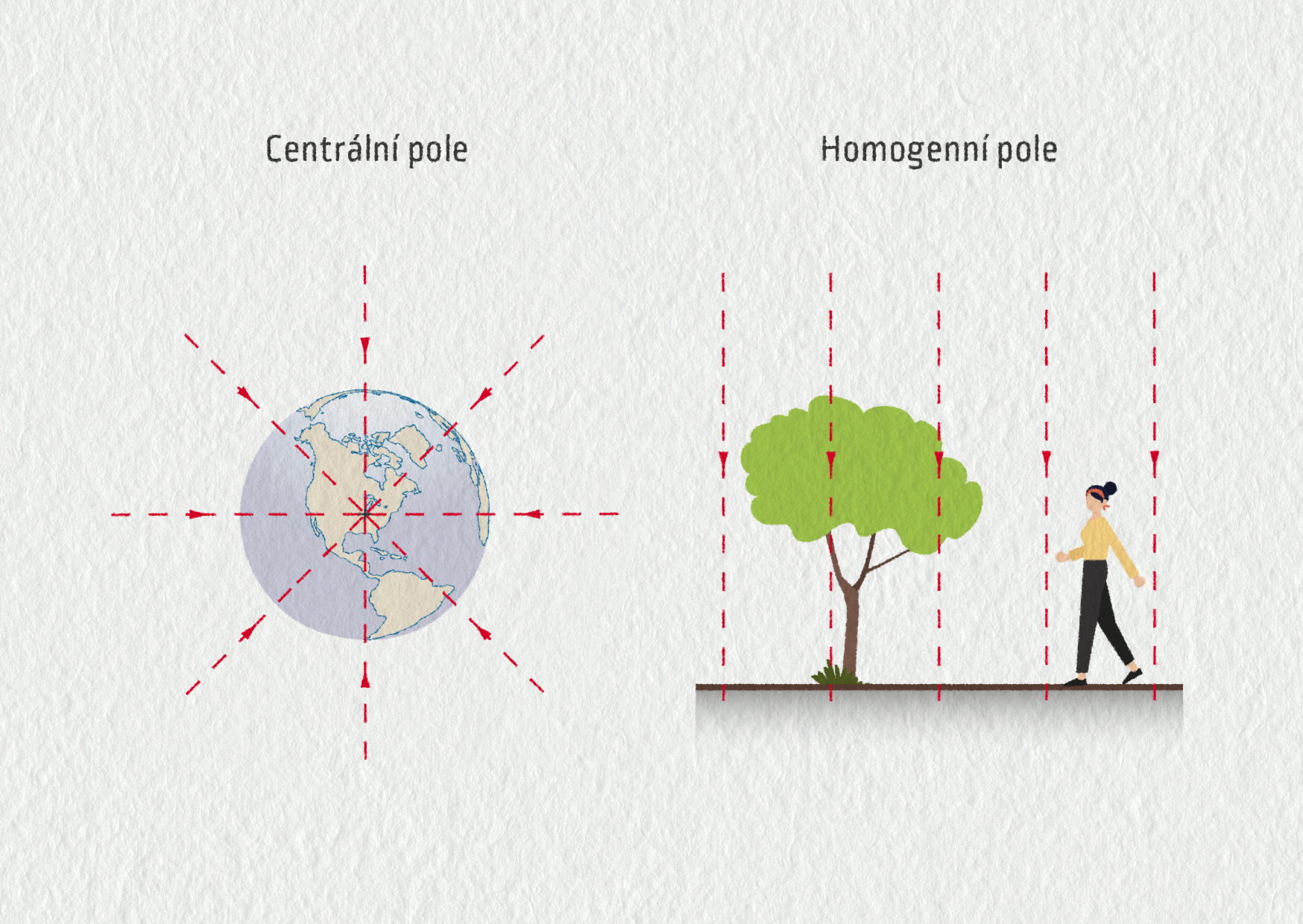
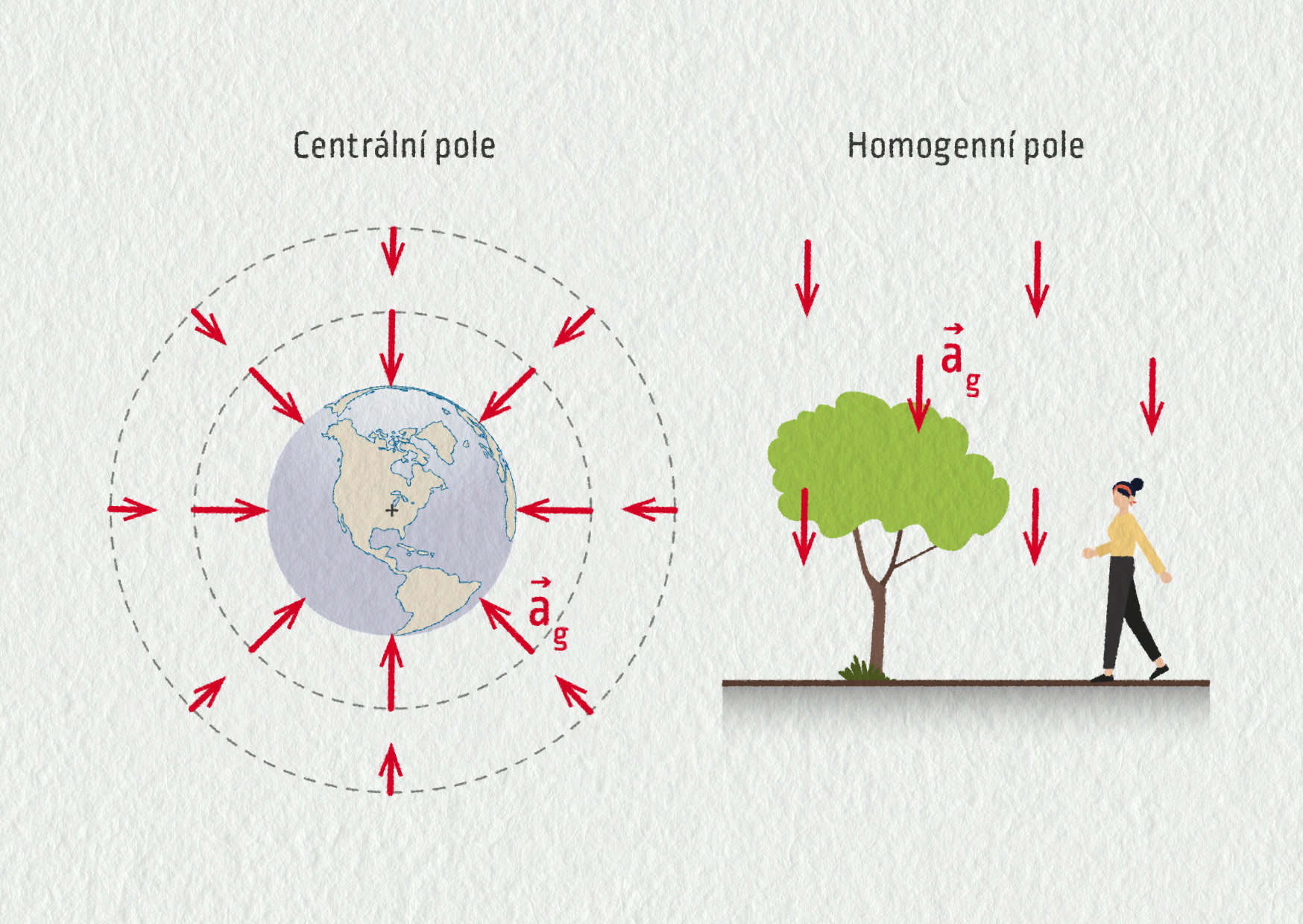
V okolí sféricky symetrických těles, typicky v okolí planet a hvězd, se siločáry paprsčitě sbíhají. Takové pole nazýváme centrální.

Pokud studujeme mechanické pohyby jen v malé oblasti prostoru, například jen v objemu volejbalového hřiště u povrchu Země, můžeme siločáry gravitačního pole považovat za rovnoběžné. V tomto případě hovoříme o homogenním poli. Homogenní pole má ve všech místech stejné vlastnosti. Na dané těleso tedy bude v kterémkoliv místě působit síla stejné velikosti i směru.

17.24 – Centrální a homogenní pole.
Zdroj

Intenzita gravitačního pole

Gravitační pole můžeme elegantně znázornit také pomocí vektorů: do každého bodu pole umístíme vektor, který ukazuje směr gravitační síly, a jehož délka vyjadřuje, jak je pole v daném bodě silné. Odpovídající vektorová veličina se nazývá intenzita gravitačního pole a je definována vztahem

\[ \Vec{a}_\mathrm{g} = \frac{\Vec{F}_\mathrm{g}}{m}\;, \]

kde \(\Vec{F}_\mathrm{g}\) je gravitační síla působící na částici o hmotnosti \(m\), která se nachází v gravitačním poli.

Vektor \(\Vec{a}_\mathrm{g}\) popisuje gravitační pole: má směr tečny k siločáře a jeho velikost je rovna síle, kterou by gravitační pole působilo na těleso o hmotnosti 1 kg.

Vektor \(\Vec{a}_\mathrm{g}\) popisuje současně i pohyb tělesa v gravitačním poli: dělíme-li totiž sílu hmotností, dostáváme zrychlení. Tedy \(\Vec{a}_\mathrm{g}\) má význam gravitačního zrychlení, zrychlení, s jakým padají všechna tělesa v daném místě pole. Jeho jednotkou je m/s2.

17.25 – Znázornění gravitačního pole pomocí vektoru intenzity gravitačního pole \(\Vec{a}_\mathrm{g}\).
Zdroj

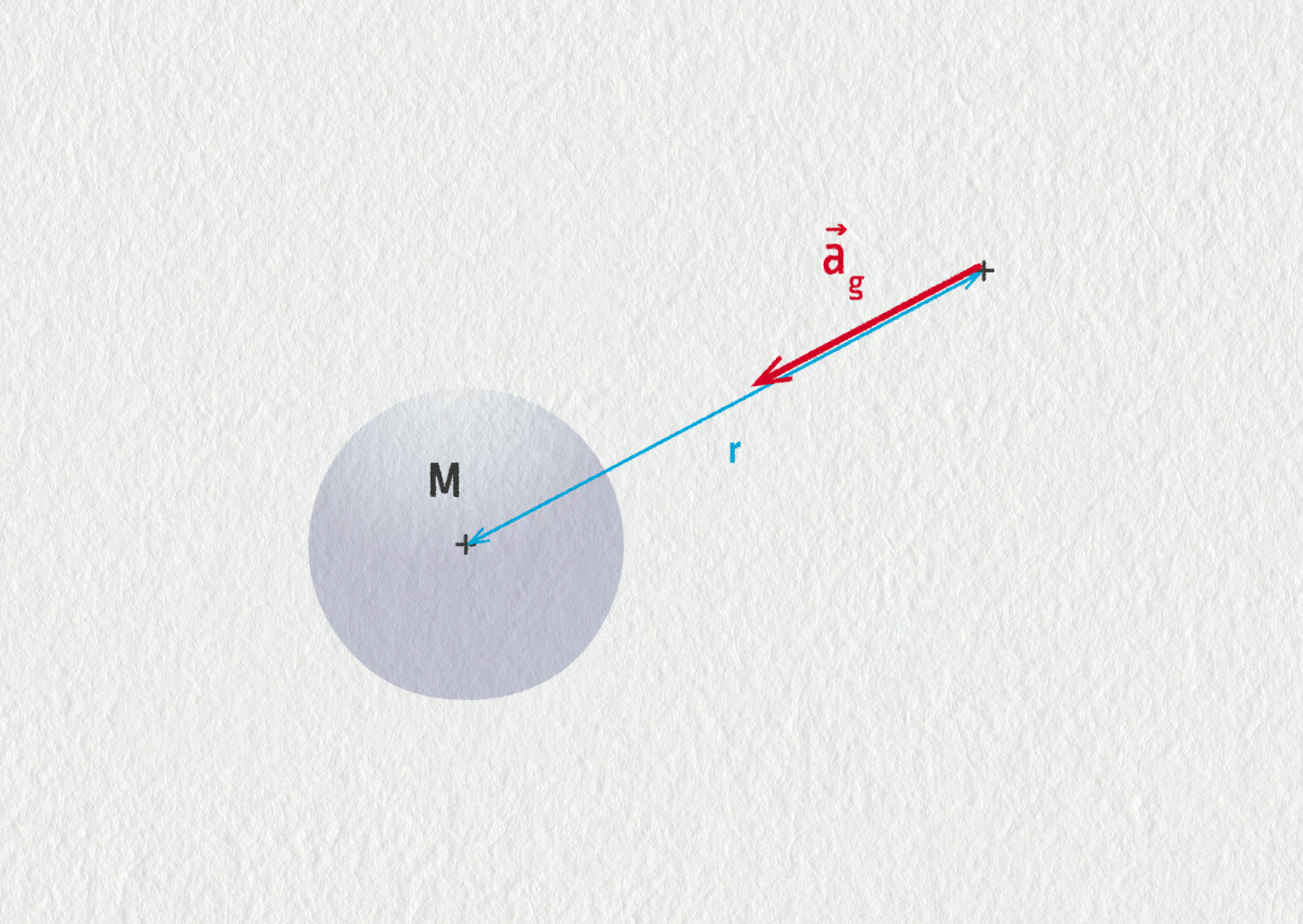
V případě centrálního pole vytvořeného tělesem o hmotnosti M z Newtonova gravitačního zákona snadno odvodíme vztah pro velikost gravitačního zrychlení:

\[ a_\mathrm{g} = \frac{F_\mathrm{g}}{m} = \frac{\displaystyle G\frac{mM}{r^2}}{m} = G\frac{M}{r^2}\;. \]

Písmeno \(r\) v předchozím vzorci značí vzdálenost místa, ve kterém pole vyšetřujeme, od těžiště sférického tělesa.

17.26 – Označení veličin ve vztahu pro gravitační zrychlení.
Zdroj

Gravitační zrychlení \(\Vec{a}_\mathrm{gZ}\) na povrchu Země spočítáme snadno dosazením za hmotnost \(M=M_\mathrm{Z}=5{,}97\cdot10^{24}\ \mathrm{kg}\) a poloměr \(r=r_\mathrm{Z}=6{,}37\cdot10^3\ \mathrm{km}\):

\[ a_\mathrm{gZ} = G\frac{M_\mathrm{Z}}{r_\mathrm{z}^2} = 6{,}67\cdot10^{-11}\cdot\frac{5{,}97\cdot10^{24}}{(6{,}37\cdot10^6)^2}\ \mathrm{m\cdot s}^{-2} = 9{,}81\ \mathrm{m\cdot s}^{-2}\;. \]

V této hodnotě zajisté poznáváte tíhové zrychlení \(g\). Jaká je přesná souvislost mezi \(a_\mathrm{gZ}\) a \(g\), je vysvětleno v poznámce níže.

Ekvipotenciální plochy

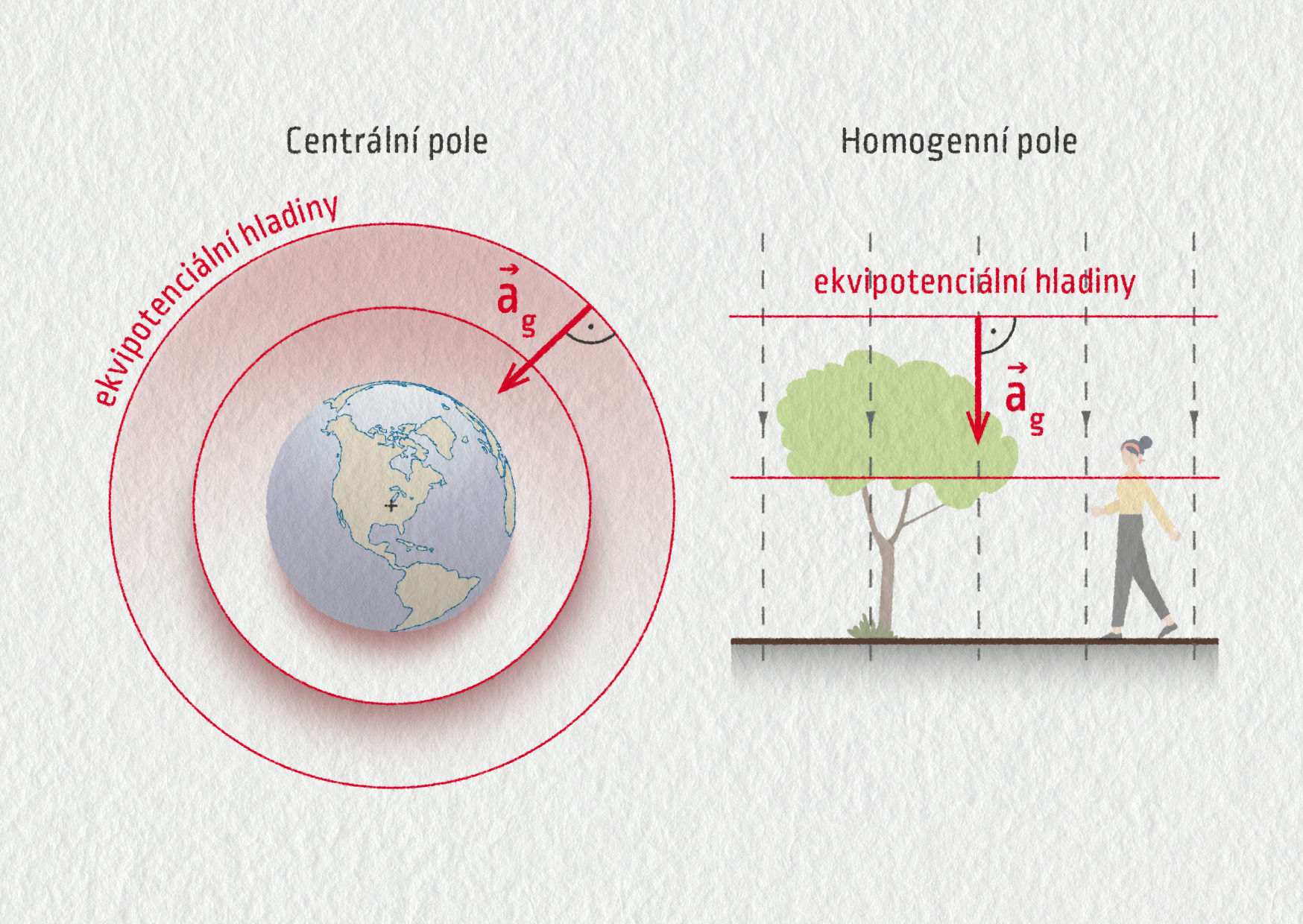
Další způsob, jak znázornit gravitační pole, využívá ekvipotenciálních ploch. Říkáme jim též ekvipotenciální hladiny nebo ekvipotenciální čáry ve 2D. Určité těleso má ve všech místech ekvipotenciální plochy stejnou potenciální energii. Ekvipotenciální hladiny jsou kolmé na intenzitu pole \(\Vec{a}_\mathrm{g}\).

17.27 – Znázornění gravitačního pole pomocí ekvipotenciálních čar.
Zdroj
Poznámka na okraj: Potenciální energie tělesa v gravitačním poli

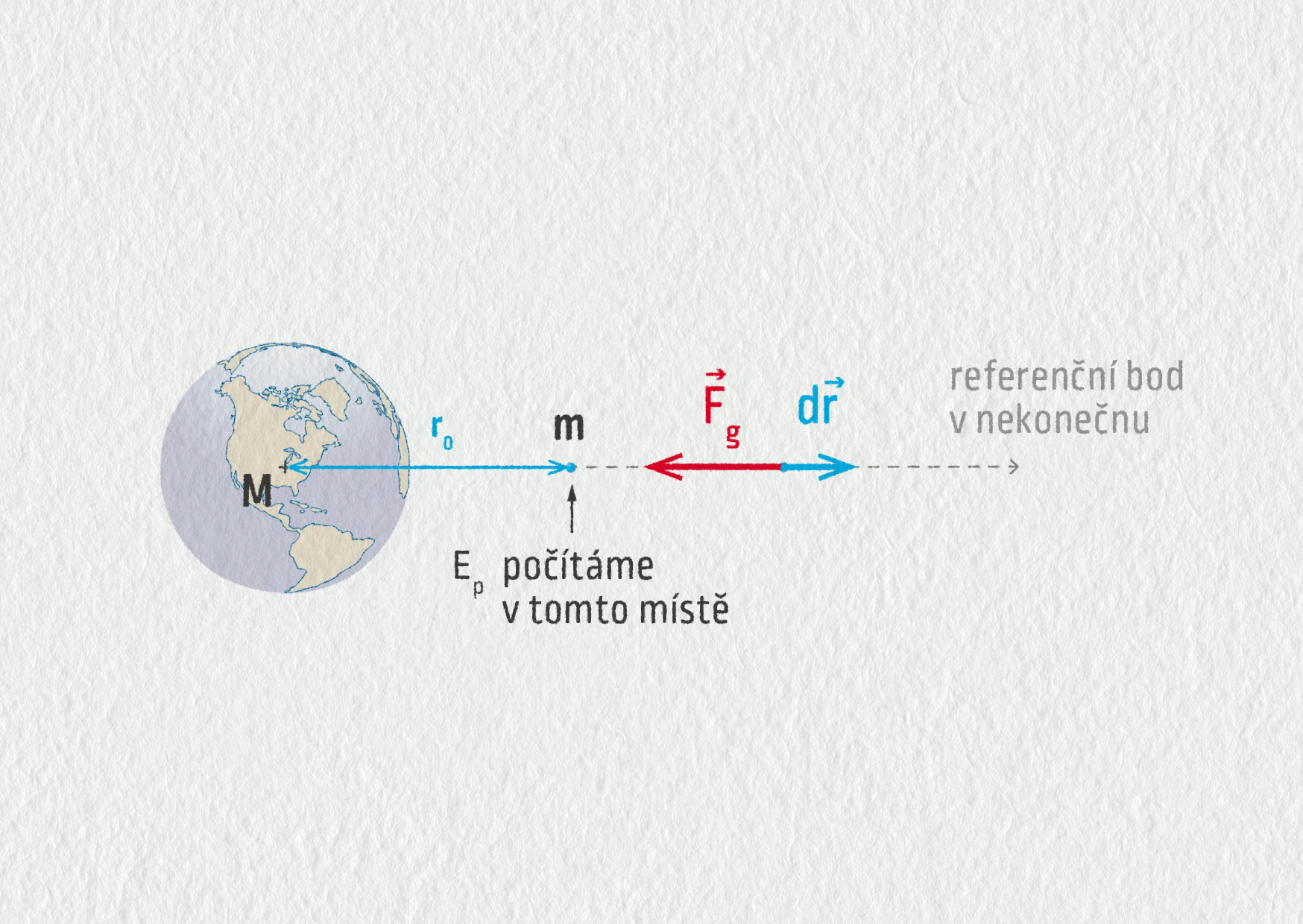
Potenciální energie tělesa v daném místě gravitačního pole je definována jakožto práce, kterou vykoná gravitační síla při přenesení tohoto tělesa z vybraného místa do předem zvoleného referenčního bodu. V případě centrálního pole se obvykle volí referenční bod v nekonečnu.

17.28 – Odvození vztahu pro potenciální energii tělesa v gravitačním poli – označení veličin
Zdroj

Z definice odvodíme vztah pro potenciální energii tělesa v centrálním gravitačním poli. Poněvadž se gravitační síla během cesty z \(r_0\) do nekonečna mění, musíme práci počítat integrálem:

\[\begin{aligned} E_\mathrm{P} &=W_\mathrm{g} = \int_{r_0}^{\infty} \Vec{F}_\mathrm{g}\cdot\mathrm{d}\Vec{r} = -\int_{r_0}^{\infty} F_\mathrm{g}\,\mathrm{d}r = -\int_{r_0}^{\infty} G\frac{mM}{r^2}\,\mathrm{d}r = -GmM\int_{r_0}^{\infty} \frac{1}{r^2}\,\mathrm{d}r\\ &= -GmM\left[-\frac{1}{r}\right]_0^{\infty} = -GmM\left[0-\left(-\frac{1}{r_0}\right)\right] = -G\frac{mM}{r_0}\\ \end{aligned}\]

Potenciální energie tělesa o hmotnosti \(m\) ve vzdálenosti \(r_0\) od středu tělesa hmotnosti \(M\), které pole vytváří, je tedy dána vztahem \(E_\mathrm{P}=-GmM/r_0\). Odtud plyne, že ekvipotenciální hladiny v centrálním poli jsou soustředné kulové plochy. Záporné znaménko vyjadřuje skutečnost, že částice \(m\) se nachází v potenciálové jámě. Pokud nemá dostatečnou kinetickou energii, je v gravitačním poli vázána, nemůže je opustit.

Studujeme-li pohyby jen v malé oblasti prostoru u povrchu Země, kde je gravitační pole téměř homogenní, volíme referenční bod na povrchu Země a gravitační sílu považujeme za konstantní. Potom

\[ E_\mathrm{P} = W_\mathrm{g} = F_\mathrm{g}h\cos(0) = G\frac{mM_\mathrm{Z}}{r_\mathrm{Z}^2}h = ma_\mathrm{gZ}h \simeq mhg\;. \]

Tíhová síla a tíhové zrychlení

Tíhová síla je gravitační síla u povrchu Země ovlivněná rotací Země. Je zvykem označovat gravitační sílu mezi libovolnými dvěma tělesy ve vesmíru symbolem \(\Vec{F}_\mathrm{g}\) a tíhovou sílu u povrchu planety symbolem \(\Vec{F}_\mathrm{G}\). Mnoho lidí tyto pojmy zaměňuje, protože v případě Země je mezi nimi jen opravdu malý rozdíl.

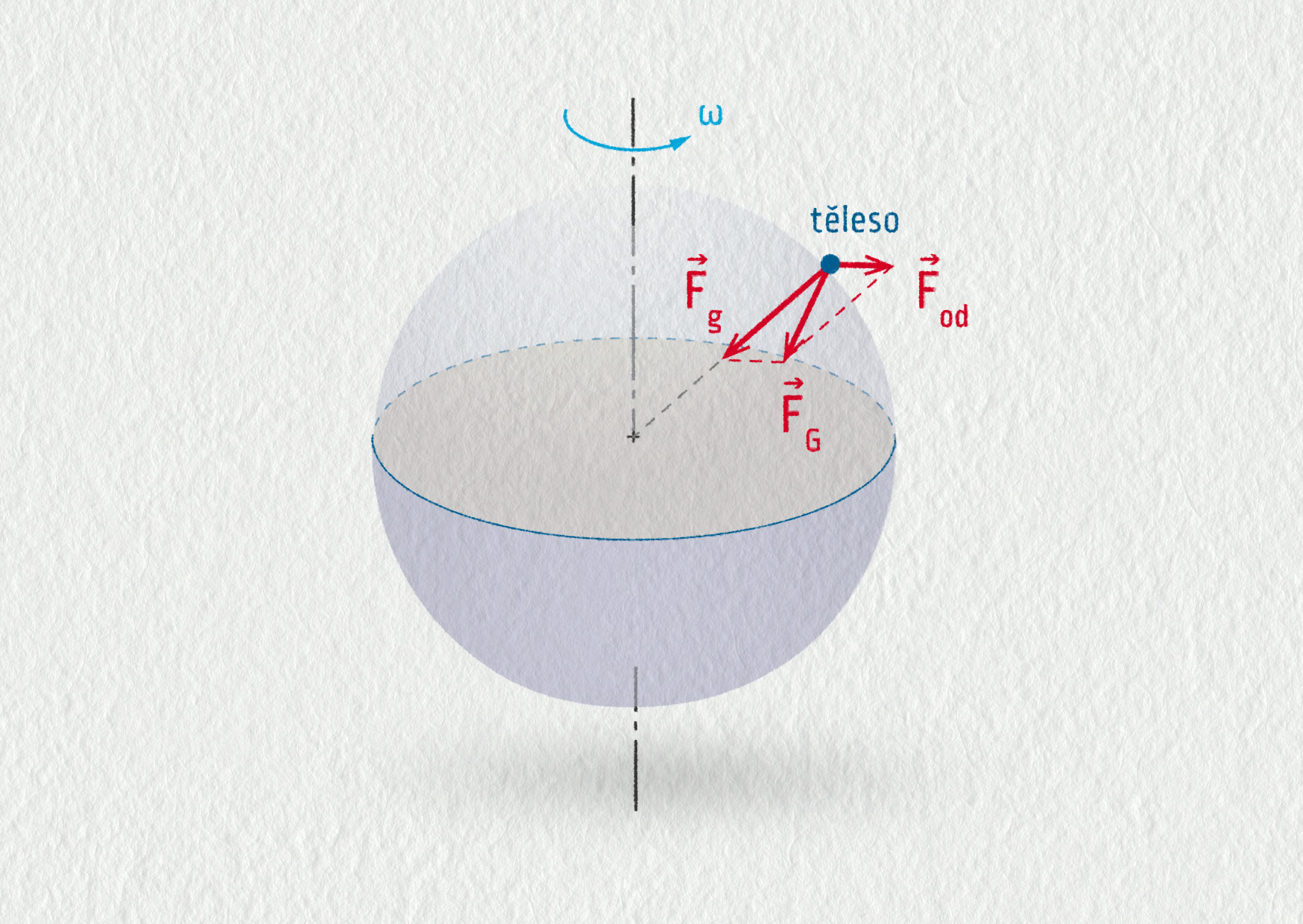
Pozorovatel fyzikálních dějů spojený s povrchem otáčející se Země tvoří, přísně vzato, neinerciální vztažnou soustavu. Kromě reálných sil, kterými na sebe tělesa skutečně působí, pozoruje i přítomnost setrvačných sil. Mezi tyto setrvačné síly patří i síla odstředivá \(\Vec{F}_\mathrm{od}\). Pozoruje tedy, že na všechna hmotná tělesa působí kromě gravitace i odstředivá síla vyvolaná rotací Země. Tíhová síla \(\Vec{F}_\mathrm{g}\) je výslednicí gravitační a odstředivé síly.

Definice tíhové síly

\[ \Vec{F}_\mathrm{G} = \Vec{F}_\mathrm{g} + \Vec{F}_\mathrm{od} \]

\(\Vec{F}_\mathrm{G}\) ... tíhová síla

\(\Vec{F}_\mathrm{g}\) ... gravitační síla

\(\Vec{F}_\mathrm{od}\) ... odstředivá síla vznikající v důsledku otáčení planety

17.29 – Tíhová síla vznikne složením gravitační síly a odstředivé síly. Tento obrázek by odpovídal velmi rychle rotující planetě, pro Zemi je odstředivá síla výrazně menší.
Zdroj

Tíhová síla definuje pro pozorovatele na Zemi svislý směr. Jednoduše řečeno, zavěsíme-li na povrchu Země těleso na provázek, má tíhová síla směr provázku. Tíhová síla je vždy kolmá na klidnou vodní hladinu v daném místě na Zemi. Když člověk stojí v klidu na váze, váha ukazuje velikost tíhové síly. Zatímco gravitační síla přitahuje tělesa přesně do středu Země, kvůli rotaci planety se zavěšená tělesa mírně vychýlí od osy otáčení (podobně jako se ze svislého směru vychýlí sedačky řetízkového kolotoče, když se kolotoč roztočí). V důsledku toho, s výjimkou pólů a rovníku, nesměřují svislé zdi domů přesně do středu Země, vodorovná hladina není přesně kolmá na spojnici daného místa a těžiště Země. Ve skutečnosti se ovšem Země otáčí pomalu, totiž s periodou 1 den, a výše popsaný efekt je hodně slabý. Odchylka směru tíhové síly od gravitační činí v ČR přibližně 0,1°, což při výpočtech můžeme směle zanedbat.

17.30 – Ke kontrole svislého směru zdí se používala olovnice – olověné těleso zavěšené na provázku. Provázek má směr tíhové síly a je kolmý na vodorovný směr. Ten můžeme ověřit pomocí vodováhy.
Zdroj

Poznamenejme, že otáčení naší planety má vliv i na její tvar. Zemský plášť je tekutý, na jeho povrchu se nachází relativně tenká zemská kůra. Klidná mořská hladina má v každém místě směr kolmý na \(\Vec{F}_\mathrm{G}\). Neuvažujeme-li suchozemský reliéf, má Země tvar rotačního elipsoidu, rovníkový poloměr je \(R_\mathrm{E}=6\,378\ \mathrm{km}\), ale poloměr měřený od pólů je o 21 km menší, totiž jen \(R_\mathrm{P}=6\,357\ \mathrm{km}\). K výpočtům se často používá střední poloměr Země \(R_\mathrm{Z}=6\,371\ \mathrm{km}\), což by byl poloměr koule o stejném objemu, jaký má Země ve skutečnosti.

Kontrolní otázka

Vyberte všechna správná tvrzení. Kdyby se Země neotáčela kolem svojí osy,



Kdyby se Země neotáčela, byla by odstředivá síla nulová. V tom případě by ovšem Země nebyla v důsledku rotace zploštělá na pólech, ale měla kulatý tvar (pomineme-li hornatý reliéf). Tíhová síla působící na určité těleso na povrchu by byla všude stejná.

Tíhové zrychlení \(\Vec{g}\) je definováno jako podíl tíhové síly \(\Vec{F}_\mathrm{G}\) a hmotnosti \(m\) tělesa, na nějž působí,

\[ \Vec{g} = \frac{\Vec{F}_\mathrm{G}}m\;. \]

Tíhové zrychlení je tedy rovnoběžné se směrem tíhové síly a určuje, s jakým zrychlením budou, z hlediska pozorovatele na povrchu Země, volným pádem padat tělesa. Tíhové zrychlení není konstanta, neboť mírně závisí na nadmořské výšce a na zeměpisné šířce.

Místo Změřené tíhové zrychlení g
Rovník, na úrovni mořské hladiny 9,780 m/s2
Zemský pól 9,835 m/s2
Praha 9,814 m/s2
Mexico City 9,776 m/s2
Mount Everest 9,773 m/s2
Kontrolní otázka
Zaškrtněte všechna správná tvrzení. Na zemském rovníku je gravitační konstanta

Žádné z nabízených tvrzení není správné. Gravitační konstanta \(G\) je konstantou úměrnosti v Newtonově gravitačním zákonu a má v celém vesmíru stejnou hodnotu \(G=6{,}67\cdot10^{-11}\ \mathrm{N}\cdot\mathrm{m}^2\cdot\mathrm{kg}^{-2}\). Tíhové zrychlení \(g\) je zcela jiná veličina, má jinou jednotku a v žádném případě je nelze porovnávat s gravitační konstantou.

Poznámka na okraj: Tíhové zrychlení podrobněji

Vezmeme-li definiční vztah pro tíhovou sílu \(\Vec{F}_\mathrm{G}=\Vec{F}_\mathrm{g}+\Vec{F}_\mathrm{od}\) a vydělíme-li jej hmotností tělesa, na které síly působí, dostaneme praktičtější vzorec pro tíhové zrychlení:

\[ \Vec{g} = \Vec{a}_\mathrm{g} + \Vec{a}_\mathrm{od}\;. \]

Velikost gravitačního zrychlení počítáme ze vztahu \(a_\mathrm{g}=GM/R^2\) a velikost odstředivého zrychlení ze vztahu \(a_\mathrm{od}=v^2/r\), kde \(v\) a \(r\) jsou rychlost tělesa a poloměr jeho trajektorie vůči inerciální geocentrické vztažné soustavě.

Poznámka na okraj: Setrvačné síly

O setrvačných silách jsme se krátce zmínili v poznámce v kapitole 5. Připomeňme si, že tyto síly existují jen v neinerciálních vztažných soustavách. Nevznikají vzájemným působením mezi tělesy, ale jako důsledek zrychleného pohybu samotného pozorovatele fyzikálních dějů. Proto se jim říká též zdánlivé neboli fiktivní síly.

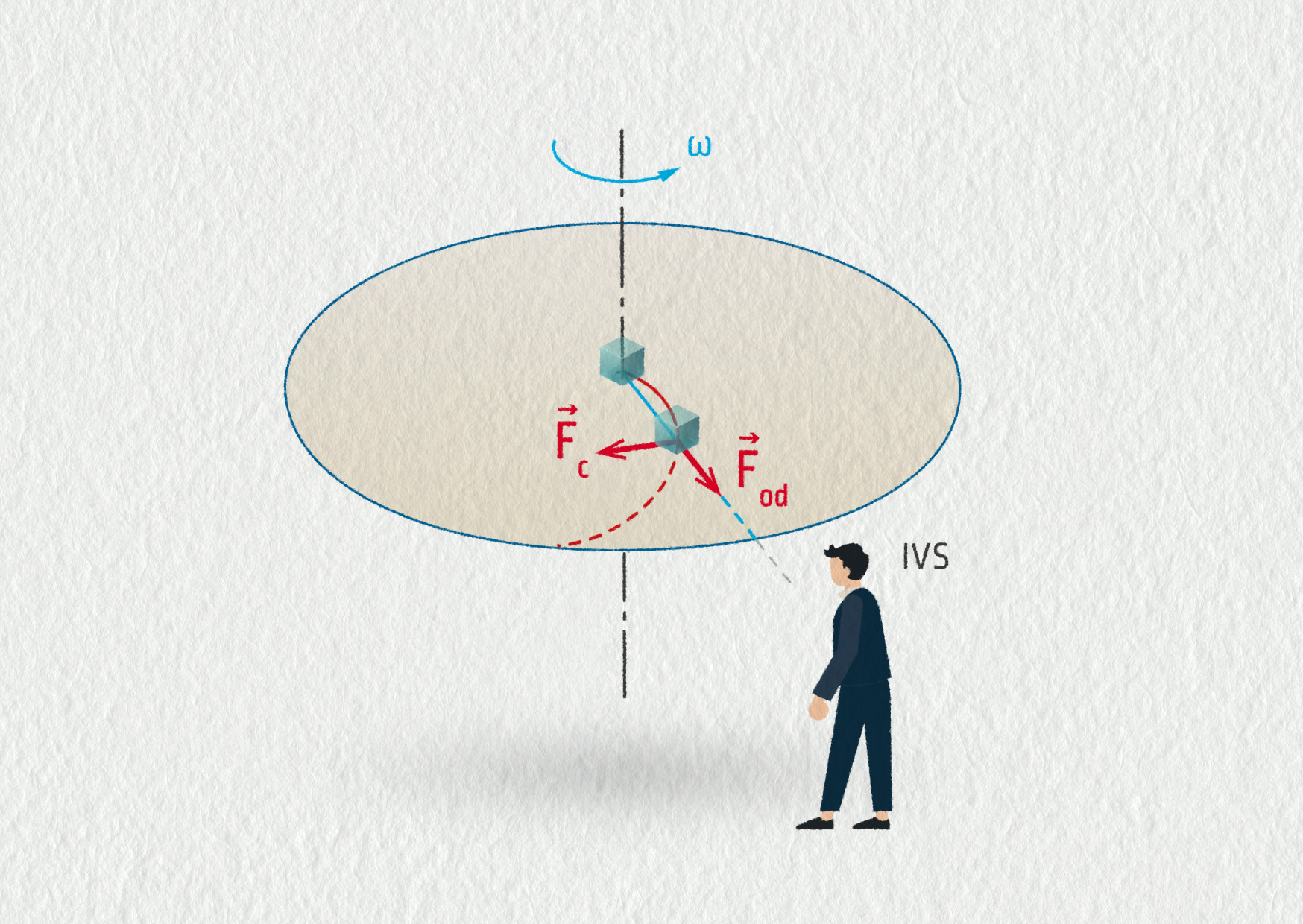
Pokud se pozorovatel pohybuje rovnoměrně po kružnici, má pocit, že na tělesa v jeho okolí působí kromě reálných sil i síla odstředivá \(\Vec{F}_\mathrm{od}\) a pokud se navíc tato tělesa pohybují, ještě i Coriolisova \(\Vec{F}_\mathrm{C}\).

Připoutaný řidič v autě, který ostře projede zatáčkou, pozoruje, jak odstředivá síla vynáší od středu například neupevněnou láhev s pitím. Pozorovatel stojící mimo silnici (inerciální vztažná soustava, dále jen IVS) by žádnou odstředivou sílu nezaregistroval a naopak by potvrdil platnost prvního Newtonova zákona – láhev s pitím setrvává v pohybu rovnoměrném přímočarém, dokud nenarazí na stěnu kabiny auta. Odstředivá síla je zdánlivý efekt, který vzniká v důsledku neinerciálnosti toho, kdo se dívá. Podobně pozorovatel, který sedí na řetízkovém kolotoči a během otáčení upustí bonbon, vidí, jak se tento bonbon vzdaluje od osy otáčení, a interpretuje to jako důsledek odstředivé síly (neinerciální VS), kdežto pozorovatel stojící na zemi (IVS) vidí, jak bonbon setrvává v pohybu daným směrem.

Při rovnoměrném pohybu pozorovatele po kružnici (vůči nějaké IVS) vypočítáme velikost odstředivé síly podle vztahu \(F_\mathrm{od}=ma_\mathrm{n}^*=m(v^*)^2/r^*\), kde \(a^*\), \(v^*\) a \(r^*\) jsou zrychlení, rychlost a poloměr trajektorie pohybu pozorovatele a \(m\) hmotnost pozorovaného tělesa.

V zeměpisu jste pravděpodobně slyšeli o síle Coriolisově v souvislosti s pohybem oblačnosti nebo směrem otáčení vodních vírů na severní a jižní polokouli. Tato síla je opět důsledkem neinerciálnosti pozorovatele. Uplatňuje se u těles, která se vzdalují nebo přibližují k ose otáčení a která pozorujeme z otáčející se vztažné soustavy. Coriolisova síla je orientována proti směru otáčení pozorovatele, pokud se pozorovaný objekt vzdaluje od osy otáčení. Takže ledová kostka klouzající bez tření od středu po gramofonové desce (přímočaře z hlediska vnějšího pozorovatele, IVS) bude na této otáčející se gramofonové desce zanechávat zakřivenou vlhkou stopu. Pozorovatel spojený s deskou si tento jev vysvětlí přítomností Coriolisovy síly. Podobně oblačnost směřující v našich zeměpisných šířkách od severu k jihu (vzdaluje se od osy rotace) se v důsledku tohoto jevu bude stáčet směrem k západu (proti směru otáčení planety).

17.31 – Ledová kostka klouže téměř bez tření po rotující desce. Modrou barvou je vyznačena trajektorie z hlediska vnějšího pozorovatele (IVS), červeně pak setrvačné síly a trajektorie z hlediska pozorovatele spojeného s deskou.
Zdroj
Poznámka na okraj: Gravitace na povrchu Země z hlediska inerciální vztažné soustavy

Uvažujme těleso v klidu ležící na povrchu Země. Pokud se na něj budeme dívat z povrchu Země (neinerciální vztažná soustava), musíme uvažovat tíhovou sílu a počítat s tíhovým zrychlením.

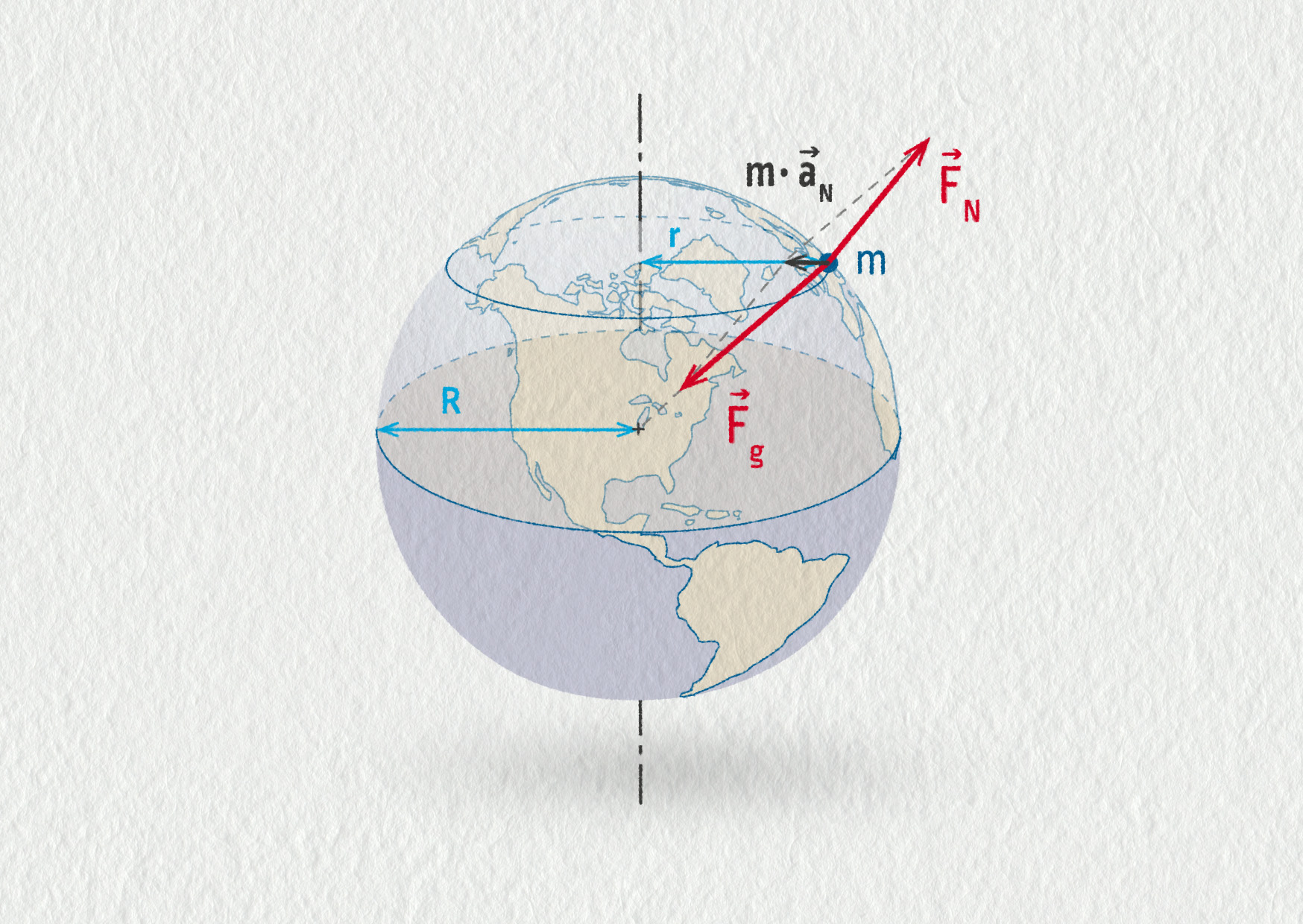
Na totéž těleso se můžeme ovšem podívat i z hlediska inerciální vztažné soustavy spojené se stálicemi. V této pozorovací soustavě se žádné setrvačné síly neuplatňují, platí Newtonovy pohybové zákony. Na toto těleso působí pouze reálné síly: gravitační síla \(\Vec{F}_\mathrm{g}\) a kolmá tlaková síla povrchu \(\Vec{F}_\mathrm{N}\). Jenže z hlediska této soustavy není těleso v klidu, ale pohybuje se spolu s povrchem Země po kružnici. Má tedy dostředivé zrychlení \(\Vec{a}_\mathrm{N}\). Jak ukazuje obrázek 17.32, gravitační a normálová síla se nemohou přesně vyrušit, jejich výslednice směřuje do středu kruhové trajektorie a platí

\[ \Vec{F}_\mathrm{g} + \Vec{F}_\mathrm{N} = m\Vec{a}_\mathrm{N}\;. \]

Porovnáním se vztahy uvedenými ve výkladu si můžeme povšimnout, že v tomto speciálním případě tělesa ležícího v klidu na povrchu Země platí \(\Vec{F}_\mathrm{N}=-\Vec{F}_\mathrm{G}\) a \(\Vec{a}_\mathrm{N}=-\Vec{a}_\mathrm{od}\).

17.32 – Silový diagram pro těleso ležící na povrchu Země z hlediska inerciální vztažné soustavy spojené se stálicemi.
Zdroj
Tlačítko pro návrat zpět nahoru na stránce (back to top)