Kosmické rychlosti
Newtonův gravitační zákon je fyzikální zákon s univerzální platností – platí stejně na Zemi jako ve vesmíru. Souvislost mezi pádem těles u povrchu a obíháním kolem Země Newton ukazoval následující úvahou.
Představme si, že na vysoký kopec na povrchu Země umístíme dělo, kterým budeme střílet vodorovně rychlostí \(\Vec{v}\). Zanedbáme pro jednoduchost otáčení Země a odpor vzduchu.
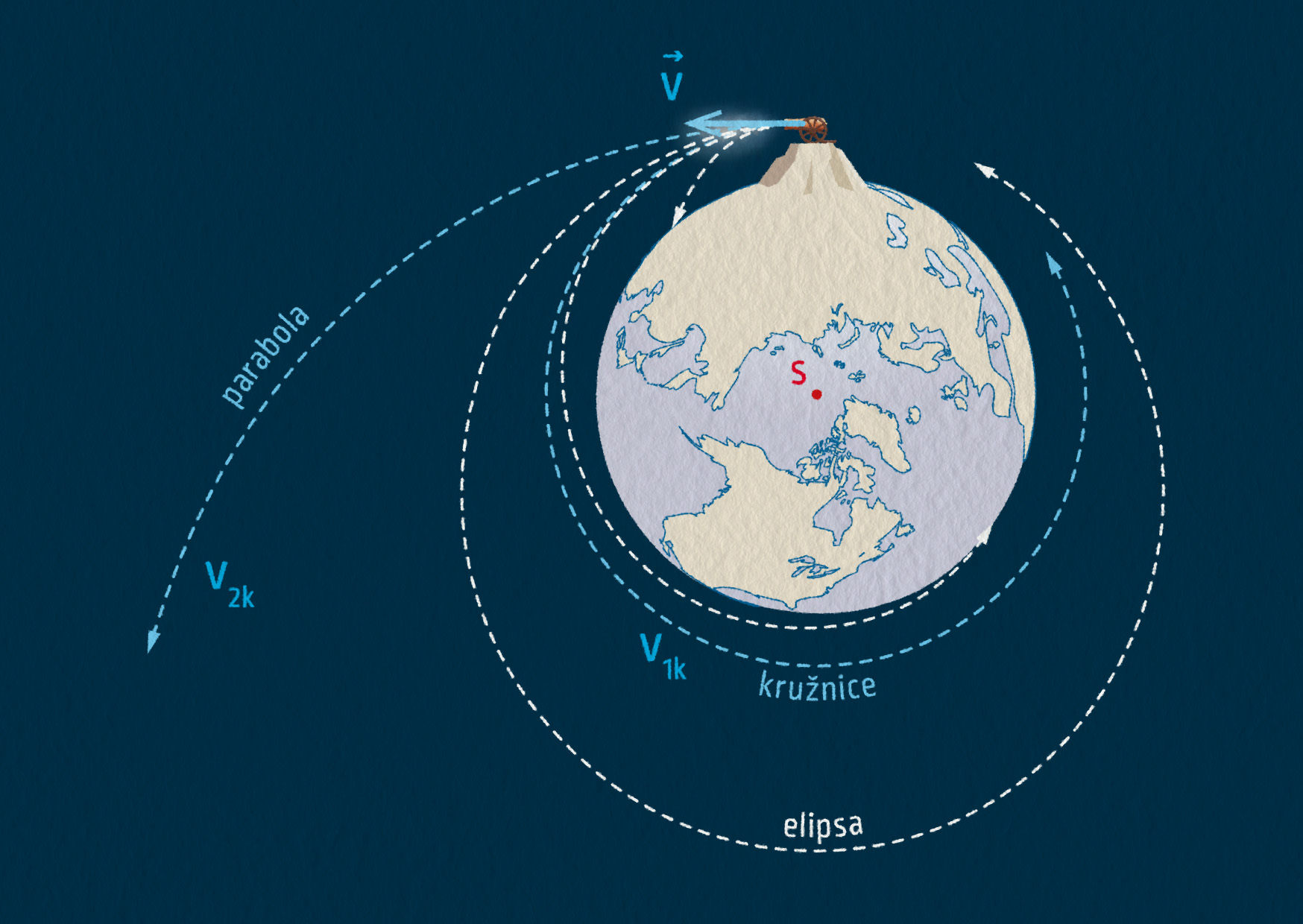
Zdroj
Pokud bude rychlost \(\Vec{v}\) malá, dopadne střela blízko od děla. Při postupném zvyšování počáteční rychlosti bude vzdálenost dopadu stále větší a větší. A při dosažení určité rychlosti nedopadne střela na povrch nikdy a začne obíhat po nejnižší kruhové trajektorii. Této rychlosti dnes říkáme první kosmická rychlost, pro Zemi má hodnotu \(v_{1\mathrm{K}}=7{,}9\ \mathrm{km/s}\). Při dalším zvětšování počáteční rychlosti střely přejde kruhový pohyb v pohyb po stále protáhlejší elipse. Jakmile dosáhneme rychlosti, kdy se elipsa již neuzavře, přechází trajektorie v parabolu. Této speciální rychlosti říkáme druhá kosmická rychlost (úniková rychlost) a pro Zemi má hodnotu \(v_{2\mathrm{K}}=11{,}2\ \mathrm{km/s}\). Překročí-li tedy rychlost střely \(v_{2\mathrm{K}}\), má tato střela dostatečně velkou energii, aby od Země odletěla libovolně daleko.
Pohyb po kruhové trajektorii v centrálním poli
K řešení obecného problému pohybu družice po elipse v centrálním gravitačním poli bychom potřebovali pokročilejší matematiku. Rozebereme tedy pouze pohyb po kružnici. Trajektorie všech planet Sluneční soustavy, trajektorii Měsíce i trajektorie mnohých umělých družic Země můžeme s dobrou přesností kruhovým pohybem aproximovat.
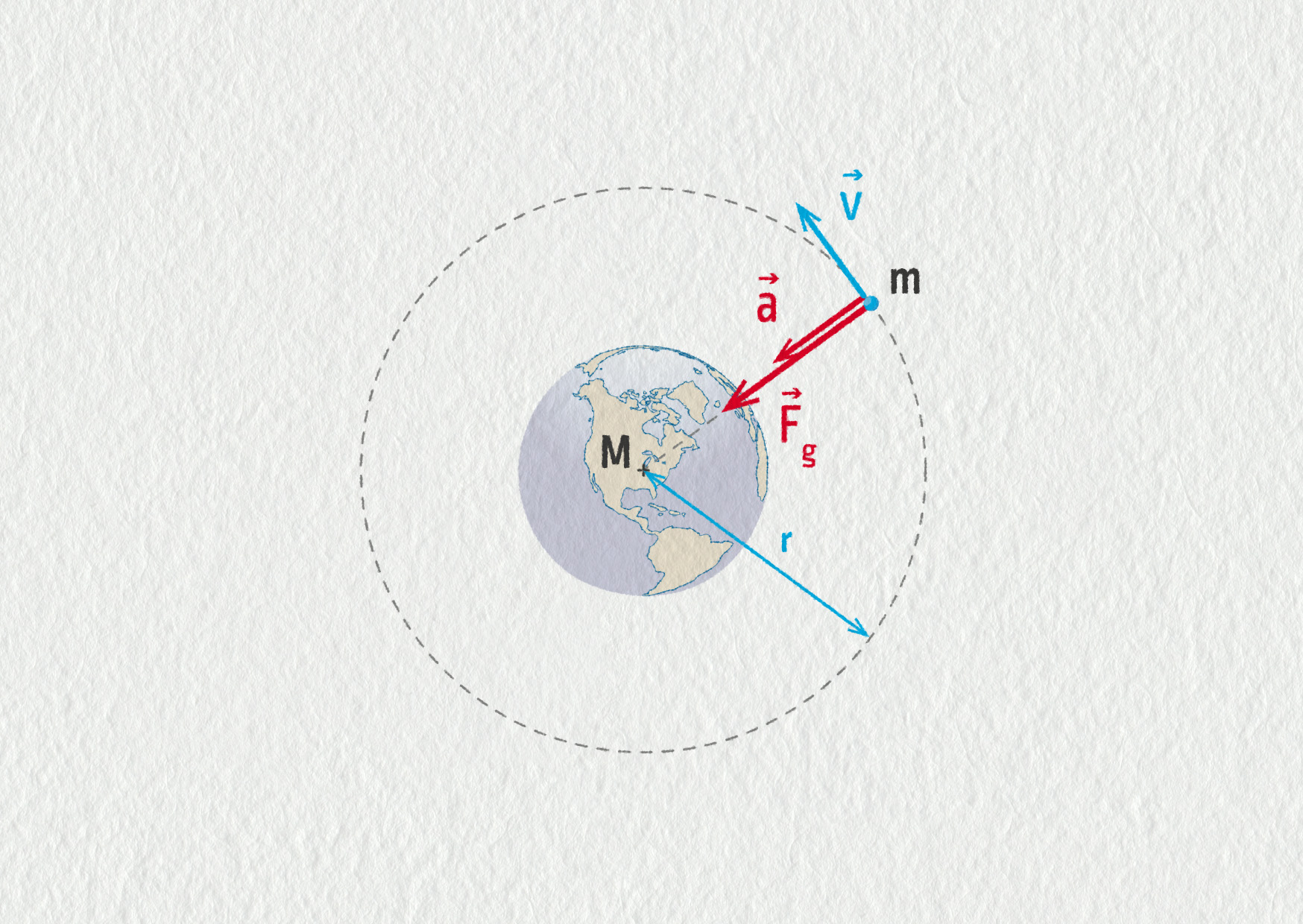
Zdroj
Na obrázku 17.34 je znázorněna družice o hmotnosti \(m\) obíhající ve stálé vzdálenosti \(r\) kolem planety o hmotnosti \(M\). Jediná síla působící na družici je gravitační síla \(\Vec{F}_\mathrm{g}\). Tato síla směřuje přesně do těžiště planety, tedy do středu kruhové trajektorie. Jelikož je tedy výslednice sil rovna \(\Vec{F}_\mathrm{g}\), platí dle 2. Newtonova zákona
\[ \Vec{F}_\mathrm{g} = m\Vec{a} \]Gravitační síla uděluje družici zrychlení \(\Vec{a}\), které má stejný směr jako působící síla (vektory \(\Vec{F}_\mathrm{g}\) a \(\Vec{a}\) jsou souhlasně rovnoběžné). Jedná se tedy o dostředivé zrychlení, známe je pod názvem normálové zrychlení \(a=a_\mathrm{N}\). Poněvadž je zrychlení kolmé na směr pohybu (na rychlost \(\Vec{v}\)), projeví se silové působení pouze zakřivováním trajektorie. Velikost rychlosti družice se měnit nemůže, neboť síla netáhne ani vpřed, ani vzad. Pohyb družice na kruhové trajektorii tedy musí být rovnoměrný.
Odvodíme nyní vztah pro rychlost družice. Pro velikosti vektorů máme z 2. Newtonova zákona
\[ F_\mathrm{g} = ma_\mathrm{N}\;. \]Po dosazení síly z gravitačního zákona
\[ F_\mathrm{g} = G\frac{mM}{r^2} \]a normálového zrychlení
\[ a_\mathrm{N} = \frac{v^2}{r} \]dostáváme
\[ G\frac{mM}{r^2} = m\frac{v^2}{r} \]odkud vyjádříme hledanou rychlost
\[ v = \sqrt{\frac{GM}{r}}\;. \]Družice na kruhové trajektorii o daném poloměru má přesně danou konstantní velikost rychlosti.
Mezinárodní vesmírná stanice, známá pod zkratkou ISS, je v současnosti jediná trvale obydlená vesmírná stanice. Mezi její hlavní cíle patří zkoumání dlouhodobého vlivu vesmírného prostředí na biologické funkce člověka: vliv mikrogravitace na svalovou atrofii, na odvápňování kostí, na oběh tělních tekutin, a vliv kosmického záření zejména na lidskou nervovou soustavu.
ISS se nachází na nízké oběžné dráze ve výšce 420 km nad zemským povrchem. Trajektorie je skloněna o 52° vzhledem k rovníku a při přeletech nad Evropou je ISS z ČR pozorovatelná jako výrazný světelný objekt na noční obloze, který se pohybuje nápadně rychleji a jiným směrem než planety a hvězdy.

Zdroj
Určete:
- rychlost pohybu ISS,
- za jak dlouho oběhne ISS Zemi.
Předpokládejme, že se ISS pohybuje po kruhové trajektorii. K výpočtu budeme potřebovat číselnou hodnotu hmotnosti Země \(M_\mathrm{Z}=5{,}97\cdot10^{24}\ \mathrm{kg}\), středního poloměru Země \(R_\mathrm{Z}=6{,}371\cdot10^6\ \mathrm{m}\) a gravitační konstanty \(G=6{,}67\cdot10^{-11}\ \mathrm{N}\cdot\mathrm{m}^2\cdot\mathrm{kg}^{-2}\). Výšku stanice nad povrchem označíme \(h\), dle zadání \(h=4{,}20\cdot10^5\ \mathrm{m}\).
a) Vzdálenost ISS od středu Země je \(r=R_\mathrm{Z}+h=6{,}791\cdot10^6\ \mathrm{m}\). Její rychlost vypočítáme dosazením do odvozeného vztahu
\[ v = \sqrt{\frac{GM_\mathrm{Z}}{r}} = \sqrt{\frac{6{,}67\cdot10^{-11}\times5{,}97\cdot10^{24}}{6{,}791\cdot10^6}}\ \mathrm{m/s} = 7{,}66\cdot10^3\ \mathrm{m/s} = 7{,}66\ \mathrm{km/s}\;. \]b) Pohyb družice je rovnoměrný, proto můžeme použít vztah
\[ v = \frac{s}{t} = \frac{\hbox{obvod}}{\hbox{dobu oběhu}} = \frac{2\pi R}{T}\;. \]Doba oběhu je tedy
\[ T = \frac{2\pi R}{v} = \frac{2\pi\cdot6{,}791\cdot10^6}{7{,}66\cdot10^3}\ \mathrm{s} = 5{,}57\cdot10^3\ \mathrm{s} \doteq 93\ \mathrm{min}\;. \]
Zdroj
Odvození třetího Keplerova zákona a vážení ve vesmíru
Pokračujme v naší úvaze o kruhovém pohybu v radiálním poli. Poněvadž je pohyb družice rovnoměrný, platí vztah \(v=s/t\). Dosaďme do něj za čas jednu periodu oběhu \(T\) a jí odpovídající dráhu rovnou obvodu kružnice:
\[ v = \frac{s}{t} = \frac{2\pi r}{T}\;. \]Je to tatáž rychlost družice, kterou jsme získali jinak – totiž z gravitačního zákona:
\[ \frac{2\pi r}{T} = v = \sqrt{\frac{GM}{r}}\;. \]Po umocnění rovnice na druhou a dalších jednoduchých matematických úpravách zjišťujeme, že
\[ \frac{r^3}{T^2} = \frac{GM}{4\pi^2}\;, \]tedy že podíl třetí mocniny poloměru trajektorie a druhé mocniny doby oběhu je konstantní a závisí pouze na hmotnosti centrálního tělesa. To je formulace třetího Keplerova zákona pro pohyb po kružnici.
Odvozený vzorec má pro astronomy mimořádný význam – umožňuje totiž vážit nebeská tělesa. Dá se použít pro vážení planet, hvězd, galaxií, černých děr, … Stačí změřit, za jak dlouho a v jaké vzdálenosti obíhá kolem tohoto objektu jiné pozorovatelné těleso. Ukažme si, jak jednoduše se dá zvážit Slunce.
Země obíhá kolem Slunce s periodou 1 rok ve střední vzdálenosti 150 milionů kilometrů. Vypočítejte hmotnost Slunce.
Pohyb Země budeme považovat za kruhový s periodou \(T=365\ \hbox{dní}=3{,}15\cdot10^7\ \mathrm{s}\) a poloměrem \(r=1{,}50\cdot10^{11}\ \mathrm{m}\). Gravitační konstanta má hodnotu \(G=6{,}67\cdot10^{-11}\ \mathrm{N}\cdot\mathrm{m}^2\cdot\mathrm{kg}^{-2}\). Ze 3. Keplerova zákona
\[ \frac{r^3}{T^2} = \frac{GM}{4\pi^2} \]vyjádříme hmotnost Slunce \(M\) a dosadíme
\[ M = \frac{4\pi^2}{G}\frac{r^3}{T^2} = \frac{4\pi^2}{6{,}67\cdot10^{-11}} \frac{(1{,}50\cdot10^{11})^3}{(3{,}15\cdot10^7)^2}\ \mathrm{kg} = 2{,}0\cdot10^{30}\ \mathrm{kg}\;. \]Geostacionární družice jsou umělé družice Země umístěné na speciální oběžnou dráhu tak, aby se nacházely stále nad stejným místem nad povrchem Země. Používají se k telekomunikaci (např. k přenosu satelitního vysílání – Skylink, Astra), k meteorologickým účelům (např. Meteosat), k pozorování Země a vesmíru. Všechny geostacionární družice obíhají nad rovníkem s periodou přesně jeden den. Vypočítejte výšku těchto satelitů nad povrchem a rychlost jejich oběhu. Rovníkový poloměr Země je \(R_\mathrm{E}=6\,378\ \mathrm{km}\), hmotnost Země \(M=5{,}972\cdot10^{24}\ \mathrm{kg}\).

Zdroj
Poloměr kruhové trajektorie družice označíme \(r\), výšku nad povrchem \(h\). Pak zřejmě platí \(r=R_\mathrm{E}+h\).
Doba oběhu \(T=1\ \hbox{den}=8{,}640\cdot10^4\ \mathrm{s}\).
Ze 3. Keplerova zákona
\[ \frac{r^3}{T^2} = \frac{GM}{4\pi^2}\;, \]vyjádříme poloměr trajektorie a dosadíme:
\[ r = \sqrt[3]{\frac{GMT^2}{4\pi^2}} = \sqrt[3]{\frac{6{,}67\cdot10^{-11}\times5{,}972\cdot10^{24}\times(8{,}640\cdot10^4)^2}{4\pi^2}}\ \mathrm{m} = 4{,}223\cdot10^7\ \mathrm{m}\;. \]Odečtením poloměru Země získáme výšku satelitu nad povrchem:
\[ h = r - R_\mathrm{E} = 4{,}223\cdot10^7\ \mathrm{m} - 6\,378\cdot10^6\ \mathrm{m} = 3{,}57\cdot10^7\ \mathrm{m}\;. \]Všechny geostacionární družice se nacházejí ve výšce přibližně 36 000 km nad povrchem.
Rychlost těchto družic vypočítáme z dříve odvozeného vztahu
\[ v = \sqrt{\frac{GM}{r}} = \sqrt{\frac{6{,}67\cdot10^{-11}\times5{,}97\cdot10^{24}}{4{,}223\cdot10^7}}\ \mathrm{m/s} = 3{,}07\cdot10^3\ \mathrm{m/s} \;. \]Geostacionární satelity se pohybují rychlostí přibližně 3 km/s.
K předpovídání počasí a sledování klimatu se používají jak geostacionární družice, tak satelity obíhající v rovině pólů. Více se dozvíte v následujícím videu: https://www.youtube.com/watch?v=Irxg-9svRtc

