Zdroj
Říká se, že Isaac Newton objevil gravitační zákon, když seděl pod stromem a na hlavu mu spadlo jablko. Představa hezká, leč hodně naivní – tak snadno fyzikální objevy nepřicházejí.
Je pravděpodobné, že během Newtonova pobytu na venkově, kam se uchýlil před epidemií moru, jej pozorování pádu jablka k úvahám o gravitaci inspirovalo. Za formulací gravitačního zákona a rozpracováním diferenciálního počtu se ve skutečnosti skrývají dva roky usilovné práce. Svoje objevy publikoval v roce 1687 v knize Principia Mathematica Philosophiae Naturalis. Toto dílo ovlivnilo na téměř tři sta let fyzikální chápání světa.
Co vlastně Newton objevil? Zjistil, že pohyby těles na Zemi se řídí stejnými zákony jako pohyby ve vesmíru. Zjistil, že volný pád jablka u povrchu Země má stejnou příčinu jako obíhání planet kolem Slunce, a tou příčinou je gravitační přitahování. Tím definitivně vyřešil spor předchozích generací, zda má Země ve vesmíru privilegované postavení, či nikoli.
Zdroj
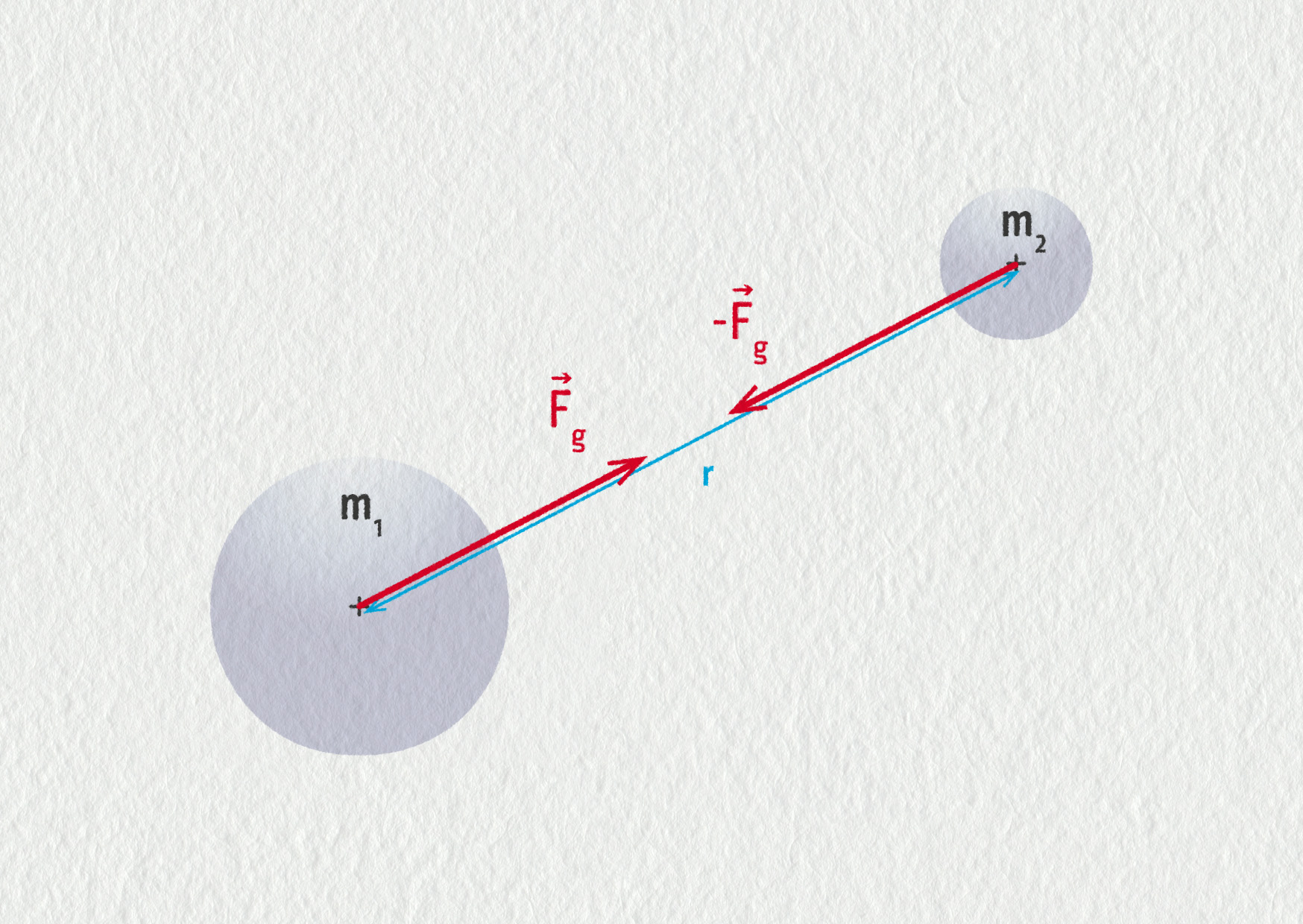
Dvě tělesa o hmotnostech \(m_1\) a \(m_2\), jejichž těžiště se nacházejí ve vzdálenosti \(r\), se vzájemně přitahují gravitační silou \(\Vec{F}_\mathrm{g}\), jejíž velikost je dána Newtonovým gravitačním zákonem.
Newtonův gravitační zákon
\[ F_g = G\frac{m_1m_2}{r^2} \]\(m_1\), \(m_2\) ... hmotnosti těles
\(r\) ... vzdálenost jejich těžišť
\(G\) ... gravitační konstanta
\(G=6,67\cdot10^{-11}\ \mathrm{N}\cdot\mathrm{m}^2\cdot\mathrm{kg}^{-2}\)
Podle třetího Newtonova pohybového zákona (zákon akce a reakce) jsou tyto gravitační síly stejně velké a opačně orientované.
Zdroj
Je třeba si všimnout, že gravitační síla je nepřímo úměrná druhé mocnině vzdálenosti.
Gravitační zákon v tomto tvaru platí pro kulově symetrická tělesa nebo tělesa, jejichž rozměry jsou zanedbatelné vzhledem k jejich vzdálenosti. Tyto předpoklady jsou výborně splněny pro pohyb planet ve Sluneční soustavě.
Velikost gravitační konstanty \(G\) nebyla za Newtonova života známa. První praktické měření provedl v roce 1798 Henry Cavendish. Gravitační konstanta \(G\) je jednou z univerzálních konstant vesmíru – kamkoli jsme se jako lidstvo dívali, všude měla stejnou hodnotu. Občas se gravitační konstanta chybně zaměňuje za tíhové zrychlení \(g\), které ovšem konstantou není, vysvětlení najdete v následující podkapitole Gravitační pole
Kontrolní otázka
Kontrolní otázka
Kontrolní otázka
Dosazením do Newtonova gravitačního zákona získáme v tomto případě pouze přibližný odhad, protože lidské tělo nelze považovat ze kulově symetrické těleso. Všimněte si, že gravitační síla mezi pasažéry je o devět řádů menší než gravitační síla, kterou je přitahuje Země. Proto pasažér cítí pouze přitažlivost zemskou, gravitační přitahování jiných lidí je zanedbatelné.
Poznámka na okraj: Jak Cavendish změřil gravitační konstantu
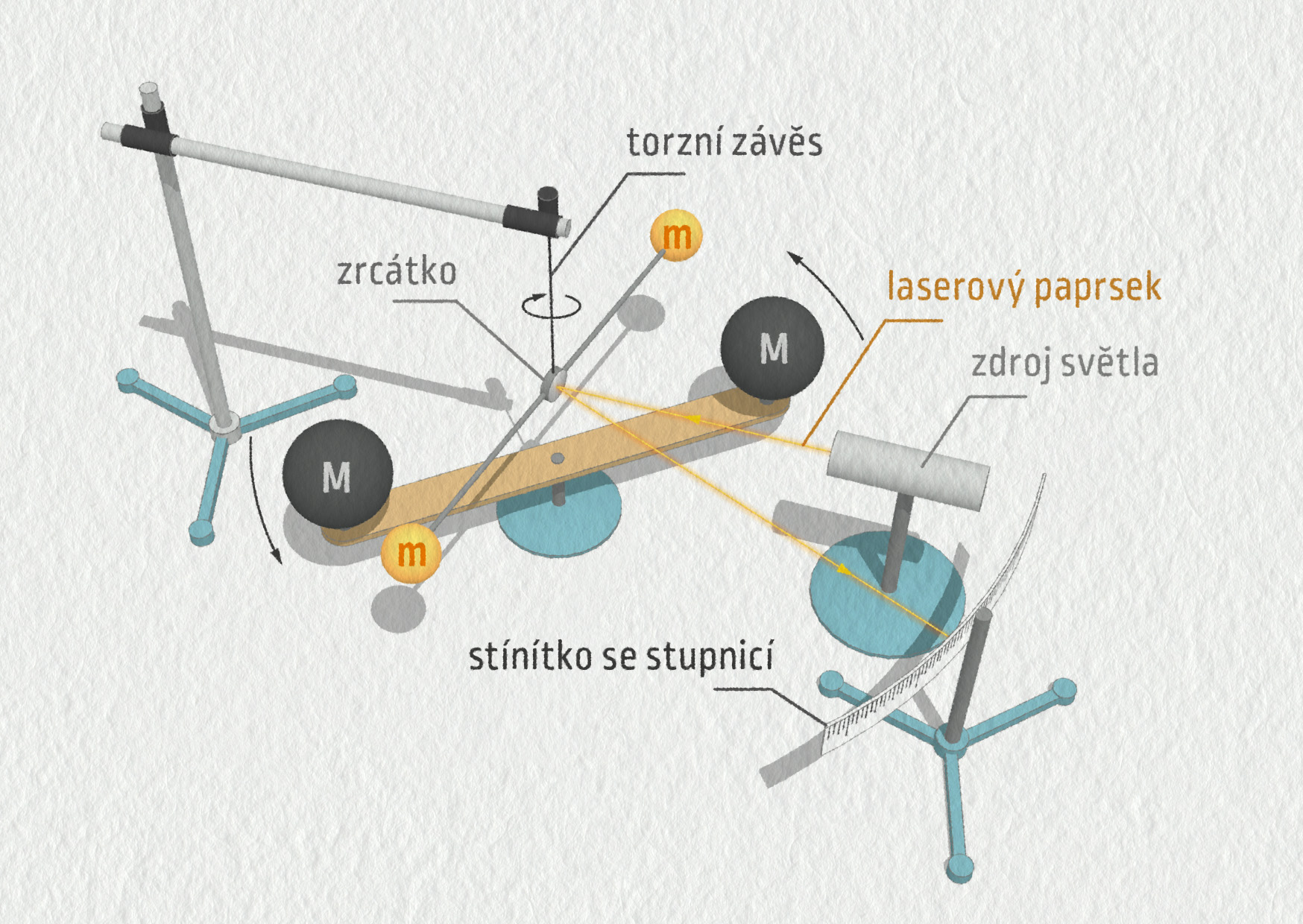
K měření použil Cavendish tenkou tyčku, na jejichž koncích byly umístěny olověné kuličky o hmotnostech \(m=730\ \mathrm{g}\). Tyčka byla zavěšena vodorovně na tenkém vlákně a byla opatřena zrcátkem – viz obrázek 17.21. Ke kuličkám střídavě z jedné a z druhé strany přibližoval pomocí nezávislého otočného ramena masivní olověné koule o hmotnostech \(m=158\ \mathrm{kg}\). Paprsek světla odražený zrcátkem byl pozorován v dalekohledu a umožnil změřit jemné otočení závěsu. Z předem zjištěné tuhosti vlákna a parametrů aparatury pak lze dopočítat gravitační sílu mezi koulemi a z ní pak gravitační konstantu.
Zdroj
Jak velkou silou se přitahují olověné koule s hmotnostmi \(m\) a \(M\), jsou-li jejich těžiště ve vzdálenosti 18 cm?
Poznámka na okraj: Heuristická úvaha vedoucí ke gravitačnímu zákonu
Uvažujme obíhání planety o hmotnosti \(m\) kolem hvězdy o hmotnosti \(M\), \(m\ll M\). Počátek soustavy souřadnic leží ve středu hvězdy, zanedbáme působení okolních těles.
-
Podle 2. Keplerova zákona je plošná rychlost planety \(\Vec{w}=\frac{1}{2}\Vec{r}\times\Vec{v}\) konstantní, takže
\[ \frac{\mathrm{d}\Vec{w}}{\mathrm{d}t} = \Vec{0} \]S využitím pravidla pro derivování součinu a vlastností vektorového součinu platí
\[ \frac{\mathrm{d}\Vec{w}}{\mathrm{d}t} = \frac{1}{2}\left(\frac{\mathrm{d}\Vec{r}}{\mathrm{d}t}\times\Vec{v}+\Vec{r}\times\frac{\mathrm{d}\Vec{v}}{\mathrm{d}t}\right) = \frac{1}{2}(\Vec{v}\times\Vec{v}+\Vec{r}\times\Vec{a}) = \frac{1}{2}\Vec{r}\times\Vec{a} = \Vec{0}\;. \]Vektorový součin průvodiče \(\Vec{r}\) a zrychlení \(\Vec{a}\) je nulový, pokud jsou tyto vektory rovnoběžné. Zrychlení planety \(\Vec{a}\) tedy musí mít směr průvodiče \(\Vec{r}\). Zrychlení směřuje do středu zakřivení trajektorie, proto musí být vůči průvodiči opačně orientované.
-
Podle 2. Newtonova pohybového zákona platí obecně \(\sum_i\Vec{F}_i=m\Vec{a}\) čili v našem případě \(\Vec{F}_\mathrm{g}=m\Vec{a}\). Gravitační síla je tedy přímo úměrná hmotnosti planety a musí mít dostředivý směr, tj. směr spojnice hvězdy a planety.
-
3. Keplerův zákon platí pro pohyb po elipse. Jelikož kružnice je speciálním případem elipsy, musí být splněn i pro kruhový pohyb:
\[ \frac{r^3}{T^2} = \hbox{konst.} \quad\hbox{neboli}\quad T^2=\frac{r^3}{\hbox{konst.}}\;. \]Pro velikost dostředivého zrychlení při pohybu planety po kružnici můžeme psát
\[ a_\mathrm{N} = \frac{v^2}{r} = \frac{\displaystyle\left(\frac{2\pi r}{T}\right)^{\!2}}{r} = \frac{4\pi^2r}{T^2} = \frac{4\pi^2r}{\displaystyle\;\frac{\strut r^3}{\hbox{konst.}}\;} = \hbox{konst.}\cdot\frac{4\pi^2}{r^2}\;. \]Velikost gravitační síly vypočítáme jako
\[ F_\mathrm{g} = ma = m\cdot\hbox{konst.}\cdot\frac{4\pi^2}{r^2} = 4\pi^2\,\hbox{konst.}\cdot\frac{m}{r^2}\;. \]Konstantu v předchozím vztahu označíme \(K=4\pi^2\,\hbox{konst.}\), takže \(F_\mathrm{g}=Km/r^2\).
-
Jelikož je gravitační přitahování symetrické, musí gravitační síla \(F_\mathrm{g}\) záviset stejným způsobem na hmotnosti planety \(m\) i na hmotnosti hvězdy \(M\). Poněvadž je \(F_\mathrm{g}\) úměrné \(m\), lze uhodnout, že konstanta \(K\) je úměrná hmotnosti hvězdy \(K=GM\). Odtud nám vychází, že velikost gravitační síly musí být
\[ F_\mathrm{g} = G\frac{mM}{r^2}\;. \]
