Dynamika kmitání

V tomto oddílu prozkoumáme, co je příčinou kmitání. Vše si vysvětlíme na dvou základních příkladech – na příkladu pružinového oscilátoru, kterým se dají modelovat složitější situace od kmitání atomů v pevných látkách až po ušní bubínek, a na příkladu matematického kyvadla, které jako model dobře funguje pro objekty zavěšené v gravitačním poli.

Kmitavý pohyb může nastat vždy, když existuje stabilní rovnovážná poloha tělesa. Při vychýlení z rovnovážné polohy na toto těleso začne působit vratná síla (často je to výslednice více působících sil), která vrací těleso zpět do rovnovážné polohy. Tato vratná síla nemůže být konstantní: při vychýlení tělesa na jednu stranu musí síla „táhnout“ směrem do rovnovážné polohy, při překmitnutí tělesa na opačnou stranu se automaticky musí změnit její orientace.

Pružinový oscilátor

Pružiny

21.17b – Tlačná pružina je součástí železničního podvozku.
Zdroj

21.17c – Pružiny jsou součástí pušek, pistolí i samopalů.
Zdroj

21.17d – Spirálové pružiny v nitru hodinek. Jedna slouží k uchování energie, druhá určuje frekvenci tikání.
Zdroj

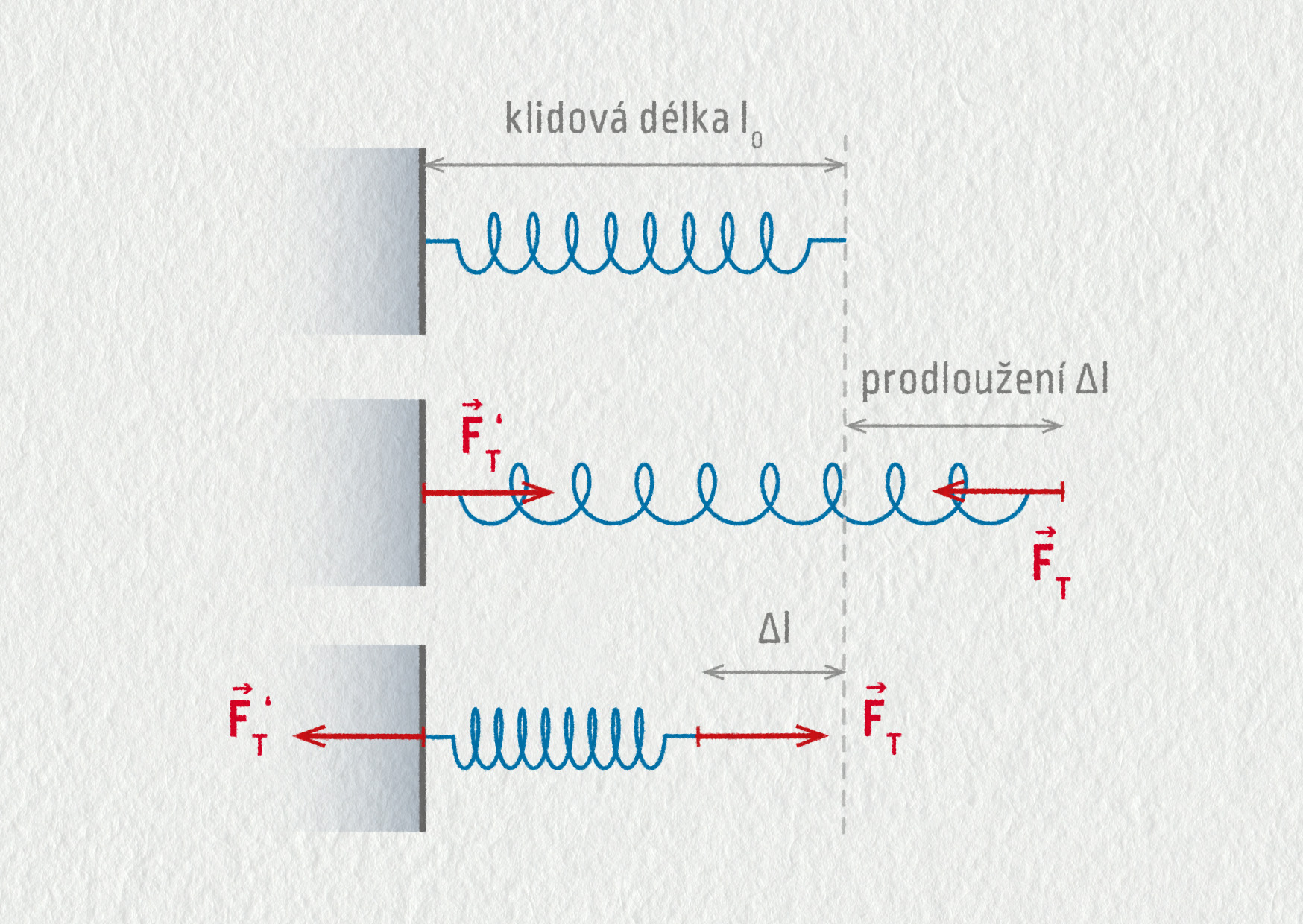
Existuje velké množství technických provedení pružin, ale všechny mají jedno společné: při natahování nebo stlačování začne pružina vytvářet sílu, díky níž se snaží vrátit se do nedeformovaného stavu. Tahová síla pružiny \(\Vec{F}_\mathrm{T}\) má směr rovnoběžný s osou pružiny, orientovaná je vždy proti deformaci. Jak jste mohli samostatně objevit v motivační aktivitě, tahová síla pružiny je přímo úměrná jejímu prodloužení, tedy

\[ F_\mathrm{T} = k\cdot\Delta l\;, \]

kde \(\Delta l\) označuje prodloužení pružiny v metrech a \(k\) je konstanta úměrnosti zvaná tuhost pružiny v newtonech na metr (N/m). Uvedený vztah je důsledkem Hookova zákona pro konkrétní těleso.

21.18 – Tahová síla pružiny **F_T** je síla, jíž deformované těleso působí na své okolí.
Zdroj

Dynamika pružinového oscilátoru

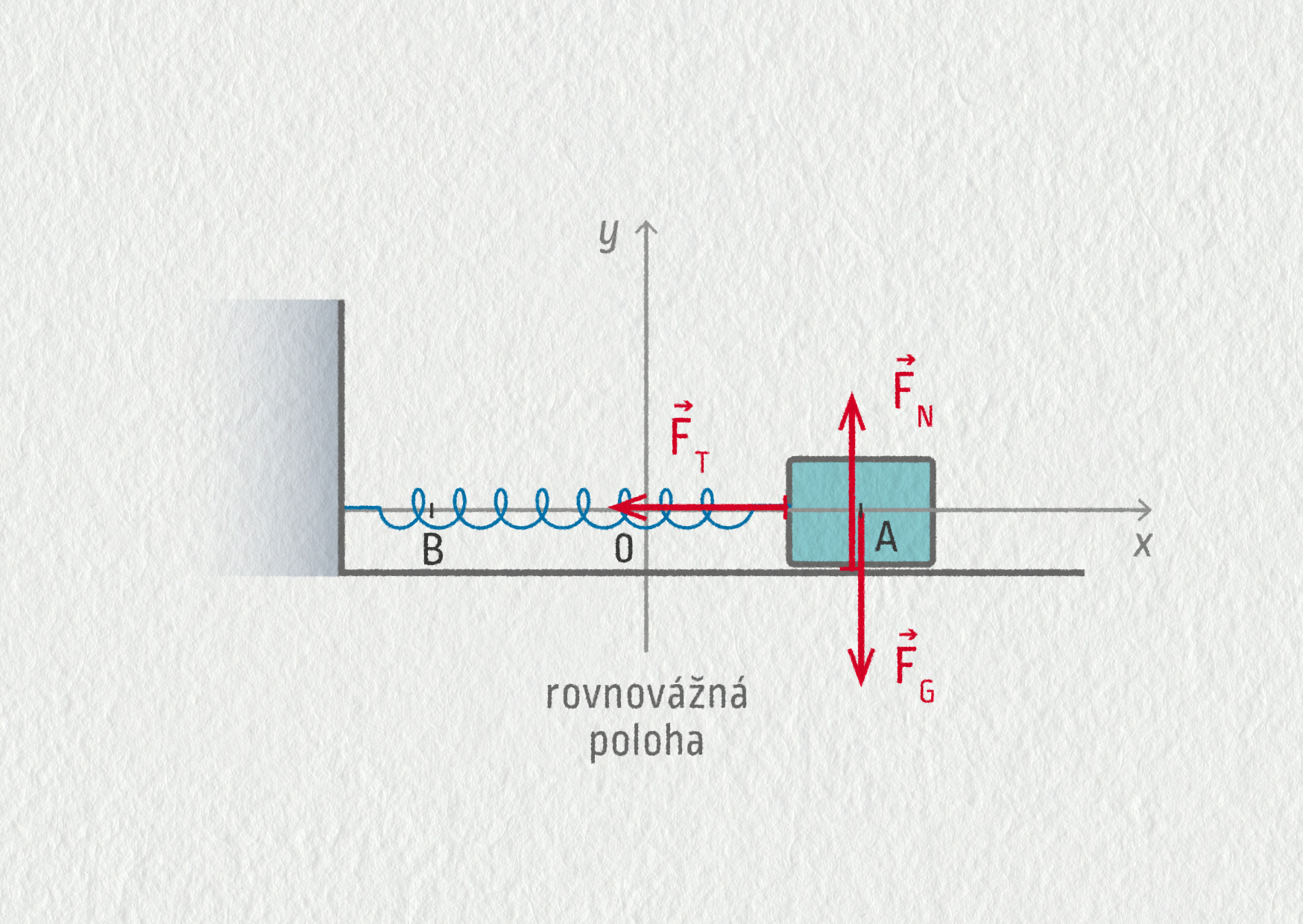
Prozkoumejme nyní pohyb tělesa pod vlivem tahové síly pružiny. Vozík o hmotnosti m položíme na hladkou vodorovnou podložku. Pružina o tuhosti k je na jednom konci upevněna k nepohyblivé stěně, její druhý konec je připojen k vozíku. V prvním přiblížení zanedbáme tření a moment setrvačnosti kol. Pokud není pružina napjatá, setrvává vozík v rovnovážné poloze. Vozík vychýlíme z rovnovážné polohy a v určitém okamžiku uvolníme bez počáteční rychlosti – viz obrázek 21.19.

Na vozík působí současně tíhová síla \(\Vec{F}_\mathrm{G}\), kolmá tlaková síla \(\Vec{F}_\mathrm{N}\) a tahová síla pružiny \(\Vec{F}_\mathrm{T}\). Vozík se pohybuje jen vodorovně, a proto se síly \(\Vec{F}_\mathrm{G}\) a \(\Vec{F}_\mathrm{N}\) musí vzájemně vyrušit. Výslednice sil je tedy rovna tahové síle pružiny \(\Vec{F}_\mathrm{T}\).

V našem případě na obrázku 21.19 je \(\Vec{F}_\mathrm{T}\) vratnou silou oscilátoru a prodloužení \(\Delta l\) je rovno okamžité výchylce z rovnovážné polohy \(x(t)\). Přímá úměrnost \(F_\mathrm{T}=kx\) znamená, že čím je oscilátor více vychýlen z rovnováhy, tím větší síla jej vrací zpět.

Jakmile těleso v bodě A uvolníme (bez počáteční rychlosti), urychluje je síla \(\Vec{F}_\mathrm{T}\) napjaté pružiny směrem doleva do rovnovážné polohy. V rovnovážné poloze O je sice síla \(\Vec{F}_\mathrm{T}\) nulová, ale těleso již získalo rychlost a setrvačností překmitne zprava doleva, tedy na opačnou stranu. Čím větší je potom výchylka vlevo od rovnovážné polohy, tím větší síla \(\Vec{F}_\mathrm{T}\) stlačené pružiny je brzdí (síla nyní působí vpravo, směrem do rovnovážné polohy), až se těleso na okamžik zcela zastaví v bodě obratu B. Situace se pak pro pohyb z B do A analogicky opakuje.

Frekvenci a periodu kmitání pružinového oscilátoru určují dvě konstanty: jednou z nich je tuhost pružiny \(k\), která nastavuje velikost vratné síly, a druhou konstantou je hmotnost kmitajícího tělesa \(m\), která charakterizuje jeho setrvačnost. Následující důležitý vztah můžete částečně objevit v praktiku a jeho odvození najdete v rozšiřující poznámce pod rámečkem. Lze jej aplikovat jak na oscilátor kmitající vodorovně, tak na oscilátor svislý.

Perioda pružinového oscilátoru

\[ T = 2\pi\sqrt{\frac mk}\;, \]

\(m\) – hmotnost tělesa v kg,

\(k\) – tuhost pružiny v N/m.

Kontrolní otázka

Zavěsíme-li na pružinu dvakrát těžší závaží, perioda kmitání se

zmenší na polovinu,
zmenší \(\sqrt2\) krát,
nezmění,
zvětší na dvojnásobek,
zvětší \(\sqrt2\) krát?

Příklad 1

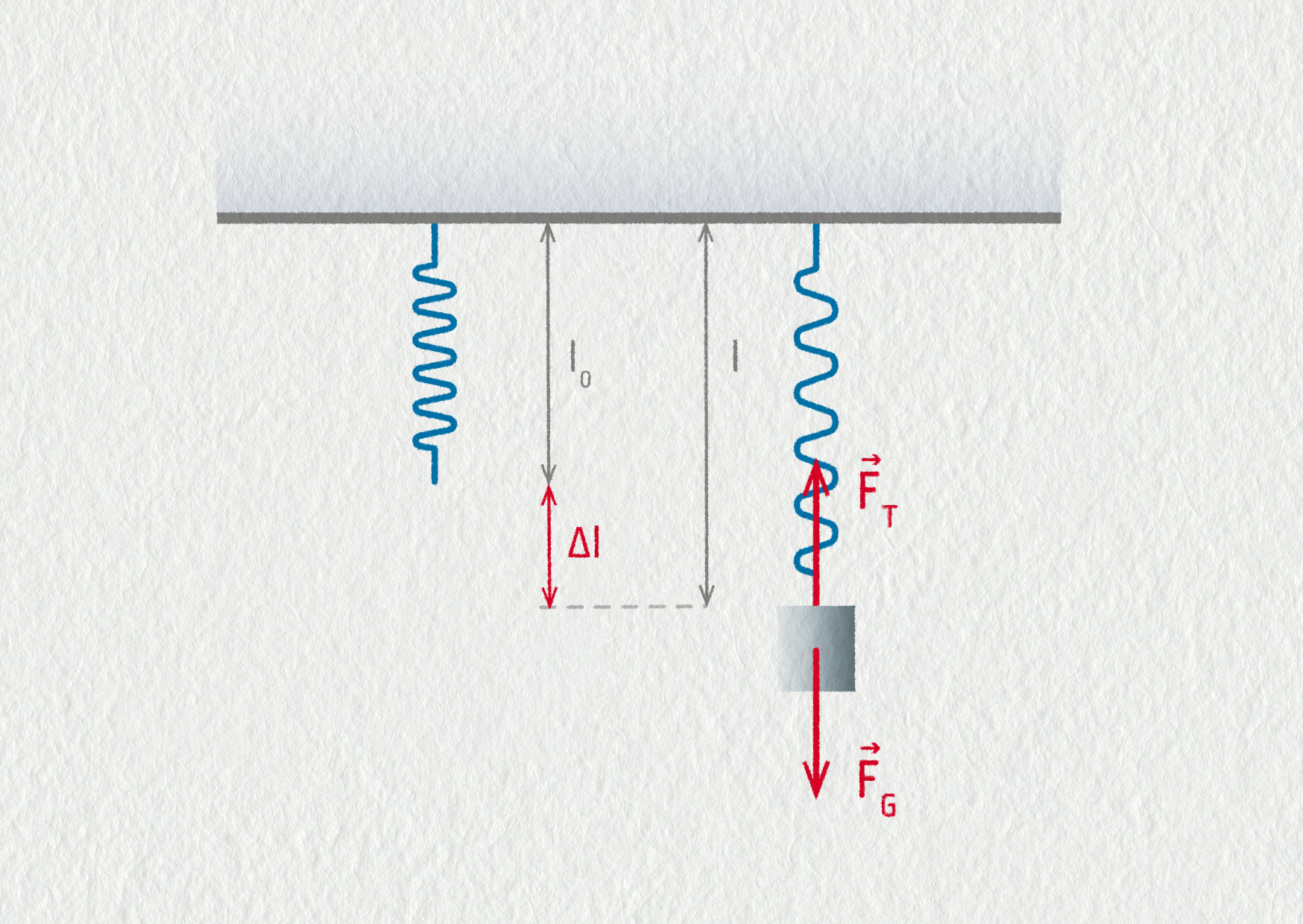
Na pružinu o klidové délce 20 cm a tuhosti 15 N/m zavěsíme závaží o hmotnosti 200 g.

Určete délku pružiny v rovnovážné poloze.
Určete frekvenci kmitání.

Řešení:

21.20 – Tahová síla pružiny – řešený příklad, označení veličin.
Zdroj

a) V rovnovážné poloze se působící síly vzájemně vyruší, platí tedy \(F_\mathrm{T}=F_\mathrm{G}\) neboli \(k\,\Delta l=mg\). Prodloužení pružiny je

\[ \Delta l = \frac{mg}k = \frac{0{,}200\cdot9{,}81}{15}\ \mathrm{m} = 0{,}13\ \mathrm{m} = 13\ \mathrm{cm}\;. \]

Délka pružiny v rovnovážné poloze je 33 cm.

b) Perioda kmitání je

\[ T = 2\pi\sqrt{\frac mk} = 2\pi\sqrt{\frac{0{,}200\ \mathrm{kg}}{15\ \mathrm{N/m}}} = 0{,}73\ \mathrm{s}\;, \]

takže frekvence \(f=1/T=1{,}4\ \mathrm{Hz}\).

Poznámka na okraj: Nalezení vztahu pro periodu pružinového oscilátoru

Vyjdeme ze situace na obrázku 21.19 ve výkladu. Pozorovatel pohybu se nachází v inerciální vztažné soustavě. Podle druhého Newtonova zákona je výslednice sil působících na těleso rovna součinu hmotnosti a zrychlení tělesa,

\[ m\Vec{a} = \sum_i \Vec{F}_i\;. \]

Promítneme-li tuto vektorovou rovnici do osy \(x\), získáváme algebraickou rovnici

\[ ma_x = -F_\mathrm{T} \]

neboli

\[ ma_x = -kx\;. \]

V předešlém oddílu jsme experimentálně zjistili, že pružinový oscilátor kmitá harmonicky. Dosaďme tedy kinematické vztahy pro výchylku \(x=x_\mathrm{m}\sin(\omega t+\varphi_0)\) a pro zrychlení \(a_x=-\omega^2x_\mathrm{m}\sin(\omega t+\varphi_0)\),

\[ -m\omega^2x_\mathrm{m}\sin(\omega t+\varphi_0) = -kx_\mathrm{m}\sin(\omega t+\varphi_0) \]

čili

\[ (m\omega^2-k)x_\mathrm{m}\sin(\omega t+\varphi_0)\; = 0. \]

Tento vztah musí být splněn v jakémkoli čase \(t\) a pro jakoukoli amplitudu \(x_\mathrm{m}\). To lze zajistit jedině tak, že první činitel je identicky roven nule:

\[ m\omega^2-k = 0\;. \]

Odsud již snadno odvodíme úhlovou frekvenci

\[ \omega = \sqrt{\frac km} \]

a periodu kmitání

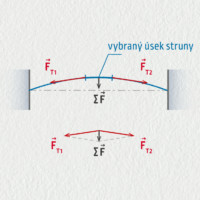
\[ T = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac mk}\;. \]

Dynamika kmitání struny na kytaře

21.21a – Atomy tvořící strunu kmitají kolem rovnovážné polohy kolmo do strany. Frekvence kmitání je rovna frekvenci vydávaného zvuku. Čím je větší amplituda kmitání, tím je tón hlasitější. Podobně jako pružina, i struna je pružný materiál. Čím víc ji napnete, tím větší silou na koncích působí.
Zdroj

21.21b – Původ vratné síly. Na struně si vybereme krátký úsek, na jehož konce působí z obou stran tahové síly **F_T1** a **F_T2**. Jejich výslednice ∑F představuje pro daný úsek vratnou sílu. Bez počítání můžeme uhodnout, že vratná síla bude tím větší, čím větší bude napětí struny, které závisí na výchylce. Kmitání je analogické pružinovému oscilátoru.
Zdroj

21.21c – Oplétání strun na hluboké tóny má velmi praktický význam. Opletením se struna stává těžší, má větší setrvačnost, a tím pádem při daném napětí kmitá pomaleji – s nižší frekvencí – než struna neopletená. Nižší frekvence znamená hlubší tón.
Zdroj

Matematické kyvadlo

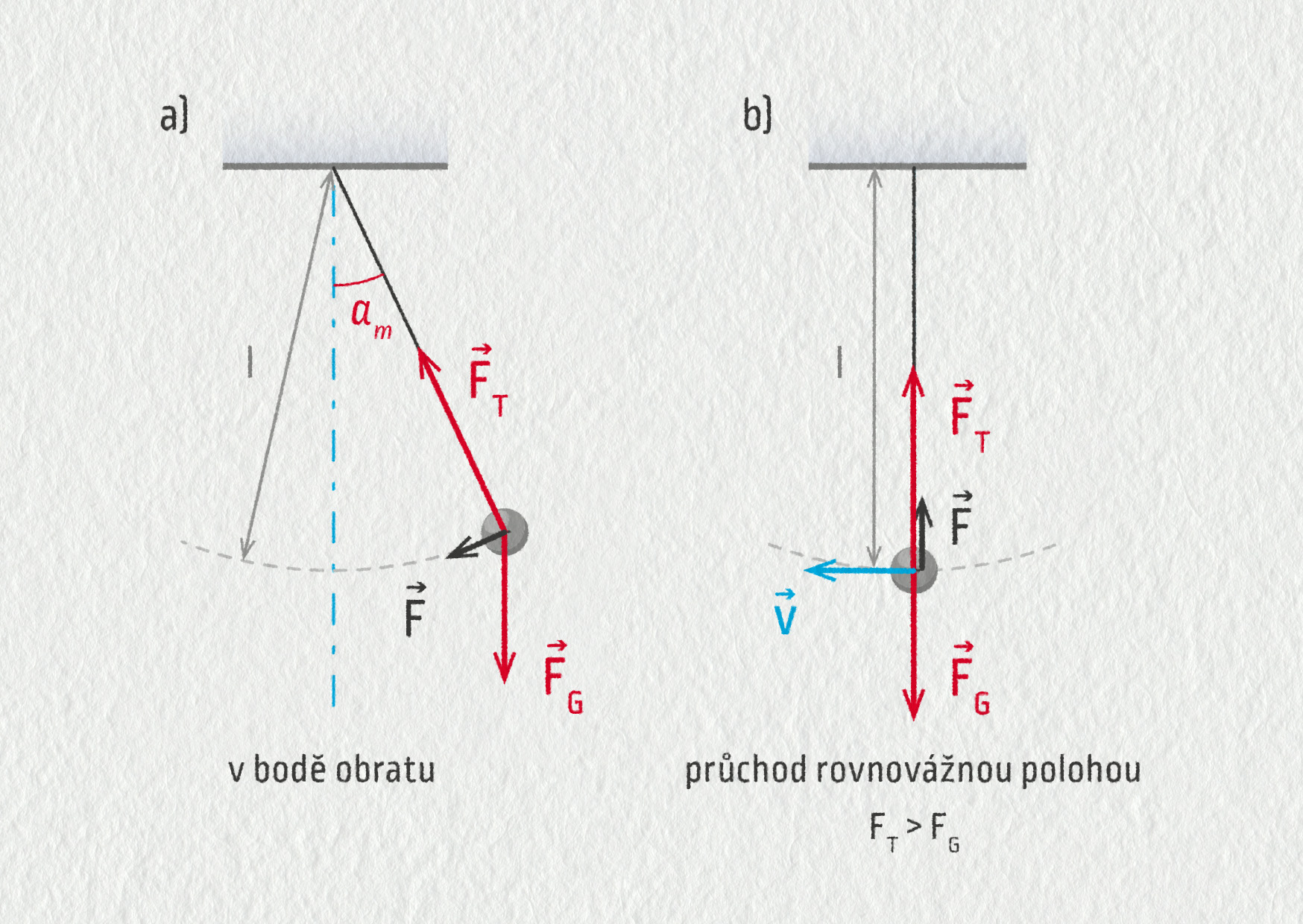
Těleso upevníme pomocí provázku k pevnému bodu závěsu. Provázek musí mít stálou délku a hmotnost zanedbatelnou v porovnání s hmotností tělesa. Symbolem \(l\) označíme vzdálenost těžiště tělesa do bodu závěsu. Použijeme těleso malých rozměrů s vyšší hustotou, abychom mohli zanedbat odporovou sílu vzduchu. Těleso vychýlíme z rovnovážné polohy a uvolníme bez počáteční rychlosti – viz obrázek 21.22 a).

21.22 – Rozbor sil působících na kyvadlo: a) v bodě obratu, b) při průchodu rovnovážnou polohou.
Zdroj

Na těleso působí tíhová síla \(\Vec{F}_\mathrm{G}\), která je po celou dobu konstantní, a tahová síla provázku \(\Vec{F}_\mathrm{N}\), jejíž směr i velikost se během kmitání mění. Složením těchto sil (vektorovým součtem) vzniká výslednice \(\Vec{F}\). Jejím vlivem vykonává těleso nerovnoměrně zrychlený pohyb po kružnici. Projekce \(\Vec{F}\) do směru pohybu je vratnou silou oscilátoru.

Za pozornost stojí i průchod rovnovážnou polohou – viz obrázek 21.22 b). Kmitající těleso v ní nesetrvává, ale pohybuje se křivočaře po kružnici o poloměru \(r=l\). Proto se síly ani v tomto bodě trajektorie při pohybu nevyruší, neboť podle druhého Newtonova zákona \(F_\mathrm{T}-F_\mathrm{G}=ma_\mathrm{N}\), kde \(a_\mathrm{N}\) je nenulové normálové zrychlení \(a_\mathrm{N}=v^2/l\).

Experimentováním v praktiku můžete samostatně objevit vztah pro periodu kmitání matematického kyvadla.

Perioda matematického kyvadla

\[ T = 2\pi\sqrt{\frac lg} \]

\(l\) – délka závěsu,

\(g\) – tíhové zrychlení.

Uvedený vztah platí pouze přibližně a používat jej můžeme jen pro kmity s malou amplitudou (tzv. malé kmity). Například pro \(\alpha_\mathrm{m}=10^\circ\) je nepřesnost tohoto vztahu 0,2 %.

Příklad 2

Kyvadla sehrála v minulosti důležitou úlohu při měření času. Vynálezem a stavbou kyvadlových hodin proslul holandský fyzik Christian Huygens. Jaká musí být délka matematického kyvadla \(l\), aby přechod z bodu obratu do protilehlého bodu obratu trval přesně jednu sekundu? Tíhové zrychlení v místě experimentu je 9,80 m/s².

Řešení:

Přechod z bodu obratu do protilehlého bodu obratu odpovídá polovině kmitu, takže perioda kmitání je \(T=2{,}00\ \mathrm{s}\). Ze vzorce pro periodu \(T=2\pi\sqrt{l/g}\) vyjádříme neznámou délku \(l\) a dosadíme číselné hodnoty.

\[ l = \left(\frac T{2\pi}\right)^2g = \left(\frac{2{,}00\ \mathrm{s}}{2\pi}\right)^2\cdot9{,}80\ \mathrm{m}\cdot\mathrm{s}^{-2} = 0{,}993\ \mathrm{m} = 99{,}3\ \mathrm{cm}\;. \]

Délka kyvadla musí být 99,3 cm.