Netlumené kmitání
Při mechanickém kmitání dochází k periodickým změnám nejen polohy a rychlosti, ale též k přeměnám forem energie. V oscilátorech, kterým jsme se podrobněji věnovali v předchozích oddílech, se mechanická energie vyskytuje v těchto podobách:
Kinetická energie \(E_\mathrm{k}=\frac12mv^2\)
Kinetickou energii má každé těleso, které se pohybuje.
Potenciální energie tíhová \(E_\mathrm{pg}=mgh\)
Potenciální energii tíhovou mají tělesa nacházející se v nenulové výšce v tíhovém poli Země. Výšku \(h\) volíme nejčastěji tak, aby byla nulová v rovnovážné poloze oscilátoru.
Potenciální energie pružnosti \(E_\mathrm{pe}=\frac12k(\Delta l)^2\)
Potenciální energie pružnosti je energie spojená s deformací pružiny. Symbol \(\Delta l\) zde označuje prodloužení pružiny vůči nenapjatému stavu. V případě oscilátoru kmitajícího vodorovně je \(\Delta l\) rovno okamžité výchylce z rovnovážné polohy \(x(t)\). Odvození vztahu pro \(E_\mathrm{pe}\) najdete v kapitole 6.
Mechanická energie je součtem energie kinetické a potenciální: \(E_\mathrm{m}=E_\mathrm{k}+E_\mathrm{p}\).
Popište přeměny energií při kmitání vozíčku na fotografii 21.19.

Zdroj
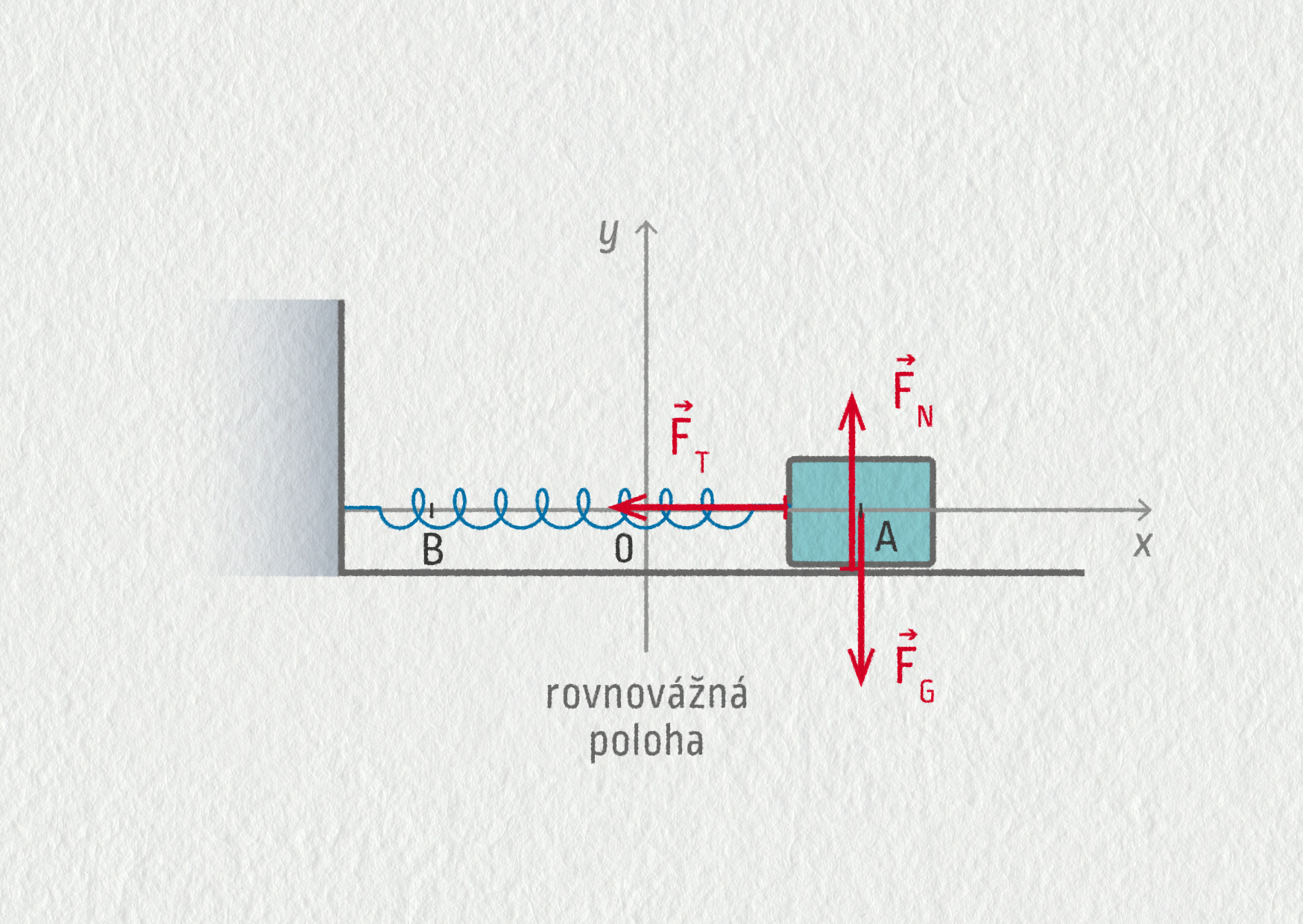
Počátek vztažné soustavy umístíme do rovnovážné polohy. Těleso se pohybuje vodorovně v nulové výšce, takže jeho potenciální energie tíhová je trvale nulová: \(E_\mathrm{pg}=0\).
V bodech obratu:
- má těleso nulovou rychlost, kinetická energie \(E_\mathrm{k}=0\),
- je pružina nejvíce napjatá, potenciální energie pružnosti \(E_\mathrm{pe}\) je maximální.
V rovnovážné poloze:
- není pružina napjatá, \(E_\mathrm{pe}=0\),
- má těleso největší rychlost, \(E_\mathrm{k}\) je maximální.
Při přechodu z bodu obratu do rovnovážné polohy se přeměňuje \(E_\mathrm{pe}\) na \(E_\mathrm{k}\), při pohybu z rovnovážné polohy do bodu obratu se přeměňuje \(E_\mathrm{k}\) zpět na \(E_\mathrm{pe}\).
Pokud v soustavě nepůsobí tření, je mechanická energie \(E_\mathrm{m}\) vozíčku konstantní, tj. součet \(E_\mathrm{k}+E_\mathrm{pe}\) má v každém okamžiku stejnou hodnotu. Oba body obratu jsou stále stejně vzdáleny od rovnovážné polohy – kmitání je netlumené.
Situace diskutovaná v předchozí řešené úloze je příkladem volného oscilátoru bez tření. Pro jeho energie můžeme shrnout:
- mechanická energie se zachovává,
- přeměňuje se kinetická energie na potenciální a naopak,
- v bodech obratu je \(E_\mathrm{k}\) nulová a \(E_\mathrm{p}\) maximální,
- v rovnovážné poloze je \(E_\mathrm{k}\) maximální,
- amplituda kmitání je stálá, kmitání je netlumené.
Pistolka pro děti je opatřena lehoučkou pružinkou o tuhosti \(k=4\ \mathrm{N/cm}\). Plastovým nábojem o hmotnosti \(m=2{,}5\ \mathrm{g}\) pružinku stlačíme o \(\Delta l=2\ \mathrm{cm}\). Při stisknutí spouště dojde k uvolnění pružinky. Jakou rychlostí je náboj vystřelen? Tření zanedbejte.
Uvažujeme pohyb vodorovným směrem a bez tření. Před výstřelem se náboj nachází v bodě A (viz obrázek 21.24), kde \(E_\mathrm{pe}\) je maximální a \(E_{\mathrm{k}A}=0\ \mathrm{J}\). Během výstřelu se potenciální energie stlačené pružinky přeměňuje na kinetickou energii náboje. V bodě B, když se pružinka přestává náboje dotýkat, již není napjatá, \(E_{\mathrm{pe}B}=0\ \mathrm{J}\) a kinetická energie náboje \(E_\mathrm{k}\) je maximální. Díky zachovávání mechanické energie můžeme psát
\[\begin{aligned} E_{\mathrm{pe}A} + E_{\mathrm{k}A} = E_{\mathrm{pe}B} + E_{\mathrm{k}B} \\ E_{\mathrm{pe}A} &= E_{\mathrm{k}B}\\ \frac12k(\Delta l)^2 &= \frac12mv_B^2\\ v_B &= \sqrt{\frac km}\,\Delta l = \sqrt{\frac{400\ \mathrm{N/m}}{0{,}0025\ \mathrm{kg}}}\cdot0{,}02\ \mathrm{m} = 8\ \mathrm{m/s}\\ \end{aligned}\]Náboj je vystřelen rychlostí 8 m/s.

Zdroj
Na tomto místě můžete oprávněně namítnout, že model oscilátoru bez tření je nereálný.
U pružinového oscilátoru zcela jistě dochází ke tření o vzduch, k vnitřnímu tření v materiálu pružiny, případně ke tření o podložku, u kyvadla obdobně nastává tření v bodě závěsu a tření o vzduch. Kvůli tření se postupně zastaví volné kmitání dětské houpačky i kmitání strojku hodinek, pokud je nenatáhnete nebo vybije-li se napájecí baterie. Samovolně se utlumí kmitání struny na kytaře, vibrace membrány reproduktoru, chvění zemské kůry při zemětřesení… Existuje vůbec v našem světě volný netlumený oscilátor?
Odpověď zní ano – ale musíme hledat nikoli mezi makroskopickými tělesy, nýbrž na úrovni molekul. Tak například molekula O2 je tvořena dvěma atomy kyslíku. Jejich rovnovážná vzdálenost je 121 pm. Vazba mezi atomy vzniká interakcí mezi elektronovými obaly a správně ji popisuje kvantová mechanika. Tato vazba není tuhá (ze statických modelů uložených ve skříni kabinetu chemie by člověk mohl získat mylnou představu tuhé tyčinky), ale podobá se spíše pružince s nelineární odezvou. To znamená, že vratná síla není přímo úměrná prodloužení, ale je to složitější spojitá rostoucí funkce. Pokud se atomy kyslíku vzdálí na více jak 121 pm, jsou taženy ke společnému těžišti, pokud se přiblíží na méně než 121 pm, jsou naopak tlačeny od sebe. Základní vibrační mód této molekuly má frekvenci 4,74 ⋅ 1013 Hz. S touto frekvencí může molekula kmitat netlumeně libovolně dlouho, amplituda těchto volných kmitů se nemění. Avšak pokud na ni dopadne infračervené záření vhodné frekvence nebo se molekula O2 srazí s jinou molekulou o dostatečné energii, může přejít do jiného vibračního módu o vyšší frekvenci a jiné amplitudě.
Tlumené kmitání
Volné kmitání tělesa je vždy tlumené. Projevuje se postupným zmenšováním amplitudy kmitání. Vlivem tření a odporu okolního vzduchu se původní mechanická energie postupně přeměňuje na vnitřní energii oscilátoru a okolí.
Zdroj
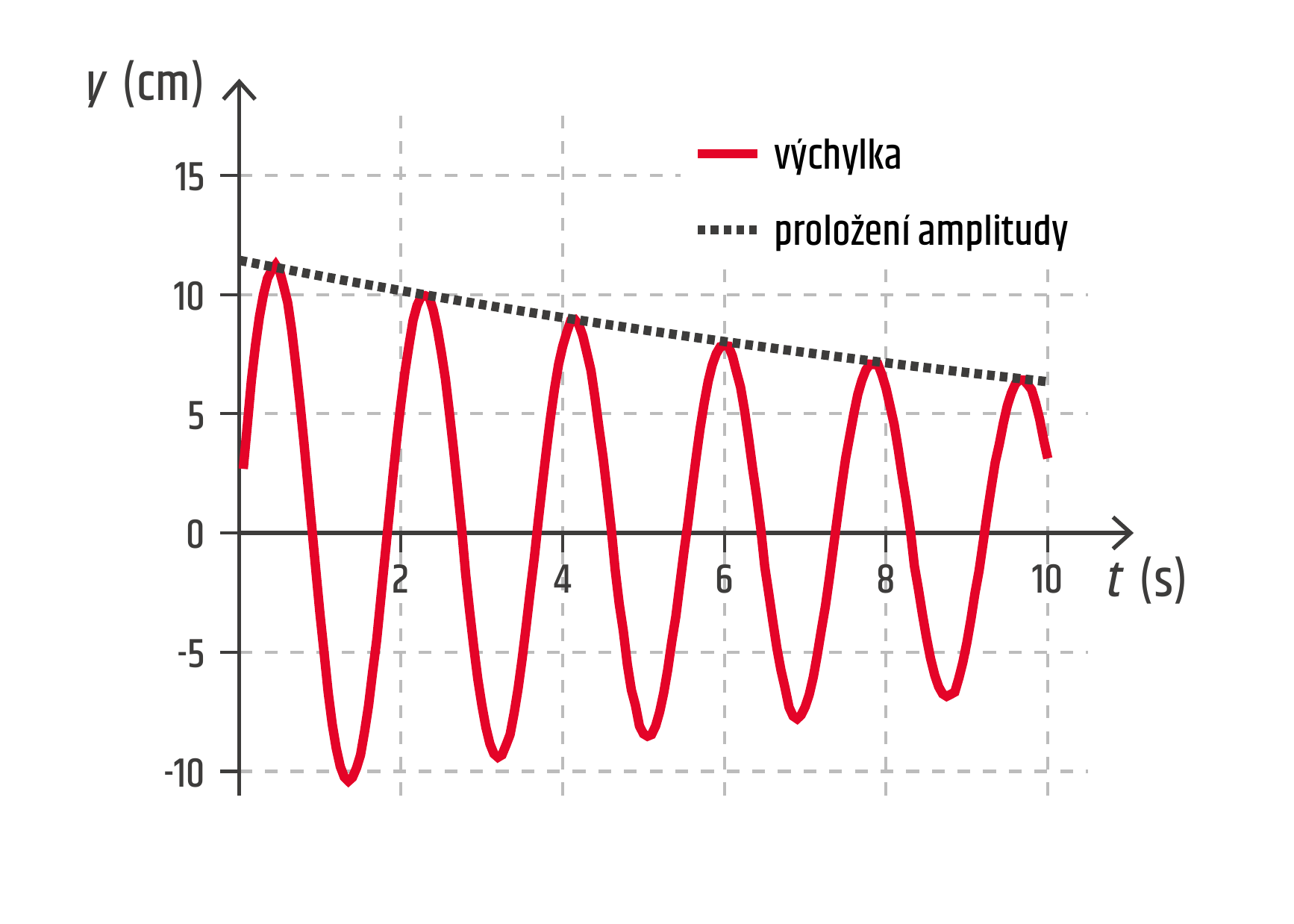
V grafu 21.25 je znázorněna závislost výchylky na čase pro vzduchem slabě tlumený oscilátor. Můžete si všimnout, že se jedná o sinusoidu, jejíž amplituda se exponenciálně zmenšuje. Pro slabě tlumený oscilátor platí
\[ y(t) = y_\mathrm{m}\mathrm{e}^{-\delta t}\sin(\omega t+\varphi_0)\;. \]Součinitel tlumení \(\delta\) určuje rychlost poklesu amplitudy k nule a závisí na třecí síle a hmotnosti kmitajícího tělesa.
Poněvadž se jednotlivé kmity neopakují identicky, hovoříme u slabě tlumeného oscilátoru o pseudoperiodickém kmitání. Pseudoperioda tlumeného oscilátoru \(T\), to znamená doba, po níž se zopakuje průběh rovnovážnou polohou stejným směrem, je delší než vlastní perioda \(T_0\) odpovídajícího netlumeného oscilátoru. Mezi úhlovou frekvencí \(\omega\) tlumeného oscilátoru a vlastní úhlovou frekvencí \(\omega_0\) příslušného netlumeného oscilátoru platí jednoduchý vztah \(\omega=\sqrt{\omega_0^2-\delta^2}\).
Se zvětšováním odporové síly se zvyšuje i součinitel tlumení \(\delta\) a kmity se tím rychleji tlumí. Je-li tlumení příliš silné (\(\delta\ge\omega_0\)), těleso ani jednou nepřekmitne přes rovnovážnou polohu, takže se vlastně žádné kmitání neobjeví.
Jak fungují tlumiče

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj
Cílem konstruktérů je najít kompromis mezi pohodlím uživatele a dobrými jízdními vlastnostmi. Vysoká tuhost zavěšení sice znamená dobrý kontakt kola s vozovkou, ale také nepříjemný pocit tvrdého pérování. Zvýšením koeficientu tlumení se zlepší pohodlí, ale snižuje se frekvence kmitání kola a zhoršuje se jeho kontakt s vozovkou.
| Vlastní frekvence (Hz) | Kvalita zavěšení |
|---|---|
| 0,5–1 | měkké, velmi pohodlné |
| 1–1,3 | pevné, docela pohodlné |
| 1,3–1,5 | tvrdé, nepohodlné |
| ≥ 1,5 | velmi tvrdé, značně nepohodlné |

