Momenty a stabilita
Ve všech úlohách počítejte s hodnotou \(g=10\ \mathrm{m/s}^2\), pokud není řečeno jinak.
Cvičení 1
Kovová tyčka se může otáčet kolem osy procházející svým středem. Tyčku nastavíme vodorovně (nachází se v rovnováze) a pak na ni zavěšujeme závaží.
- Závaží 50 g je ve vzdálenosti 4 cm od osy. Jak těžkým závažím umístěným na druhý konec ve vzdálenosti 20 cm od osy bychom tyčku vyvážili?
- Závaží 50 g je ve vzdálenosti 10 cm od osy. Kam je třeba umístit dvousetgramové závaží, aby zůstala v rovnováze?
- Závaží 50 g je ve vzdálenosti 10 cm od osy a jiné dvousetgramové závaží 5 cm na opačné straně od osy otáčení. Rozhodněte, kam je třeba zavěsit stogramové závaží, aby byla tyčka v rovnováze.
- 10 g;
- 2,5 cm od osy (na opačnou stranu);
- na stranu lehčího, 5 cm od osy
Cvičení 2
Kovová tyčka s těžištěm uprostřed je teď upevněná na svém jednom konci, kolem kterého se může otáčet. Její hmotnost je 500 g a délka 40 cm.
- Jak velkou silou musíme na druhém konci působit, abychom ji udrželi vodorovně?
- Na tyčku zavěsíme 200 g závaží 30 cm od osy otáčení. Jak velkou svislou silou působící na volném konci udržíme tyčku ve vodorovné poloze?
- V otázce b) setrvává tyčka v klidu. Vyruší se působící síly?
- 2,5 N;
- 4 N;
- ano, platí zákon setrvačnosti, na tyčku působí svislá síla v místě upevnění o velikosti 3 N
Cvičení 3
Stavební kolečko je typickým příkladem jednozvratné páky. Na kolečko si naložíme 3 pytle cementu (3 × 25 kg) tak, že těžiště nákladu je ve vodorovné vzdálenosti 40 cm od osy (od osy gumového kola).
- Jak velkou svislou silou musíme při jízdě na kolečko působit na konci rukojetí ve vodorovné vzdálenosti 150 cm od osy? Neuvažujte hmotnost samotného kolečka.
- Řešte tutéž úlohu za předpokladu, že stavební kolečko váží 30 kg a jeho těžiště leží ve vodorovné vzdálenosti 25 cm od osy.

Zdroj
- 200 N;
- 250 N
Cvičení 4
Louskáček na ořechy je příkladem jednozvratné páky. Má délku 25 cm, oříšek je umístěn 4 cm od osy. Jakou silou je drcen oříšek, když na konci rukojetí zmáčkneme silou 100 N?

Zdroj
625 N
Cvičení 5
Otvírač nápojů je dalším příkladem jednozvratné páky. Má délku 20 cm, na jednom konci jej položíme na víčko shora (bod otáčení), 3 cm od tohoto konce zahákneme za víčko. Jak velkou silou otvírač tahá za víčko, když na rukojeť působíme silou 15 N ve vzdálenosti 12 cm od bodu otáčení??

Zdroj
60 N
Cvičení 6
Dětská houpačka je příkladem dvojzvratné páky. Je sestavena z prkna o délce 3 m podepřeného v těžišti (osa otáčení). Na jeden konec si sedne Natálka (hmotnost 20 kg). Jak daleko od osy si má sednout Martin (hmotnost 30 kg), aby byla houpačka v rovnováze?

Zdroj
1,0 m
Cvičení 7
Martin je nespokojen, protože by také chtěl sedět na konci. O kolik cm a na kterou stranu musí posunout prkno z předchozího příkladu, aby byla houpačka opět v rovnováze?
- Hmotnost prkna neuvažujte.
- Hmotnost prkna je 15 kg.
- těžiště prkna posunout o 30 cm od podpěry směrem k Natálce;
- těžiště prkna posunout o 23 cm od podpěry směrem k Natálce
Cvičení 8
Betonový nosník o hmotnosti 60 kg a délce 2,4 m leží vodorovně na dvou podpěrách. Jedna podpěra se nachází na jednom konci a druhá 40 cm od druhého konce. Namalujte si obrázek a vypočítejte, jakými silami působí podpěry na nosník.
240 N a 360 N
Cvičení 9
Vodorovný nosník o hmotnosti 700 kg s těžištěm uprostřed je zatížen dvěma silami – viz obrázek 16.46. Vypočítejte síly, kterými podpěry působí na nosník.
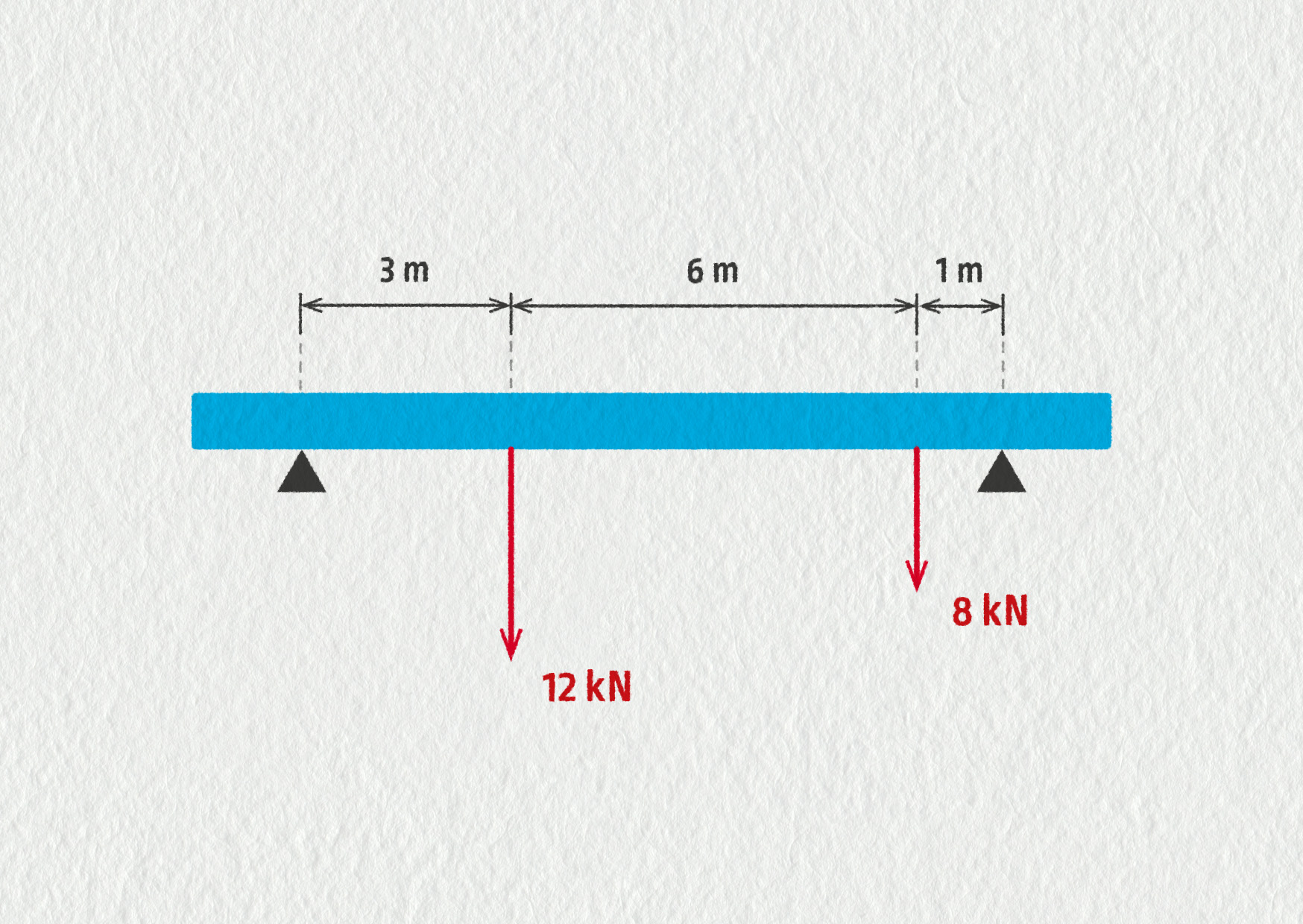
Zdroj
- 14,3 kN;
- 12,7 kN
Cvičení 10
Na obrázku 16.47 je znázorněn žebřík opřený o zeď. Jeho délka je 8,00 m, hmotnost 20 kg, úhel, který svírá se svislým směrem, je 30°. Přepokládejme, že jeho těžiště leží uprostřed. V obrázku 16.47 jsou vyznačeny působící síly, jejichž velikosti jsou:
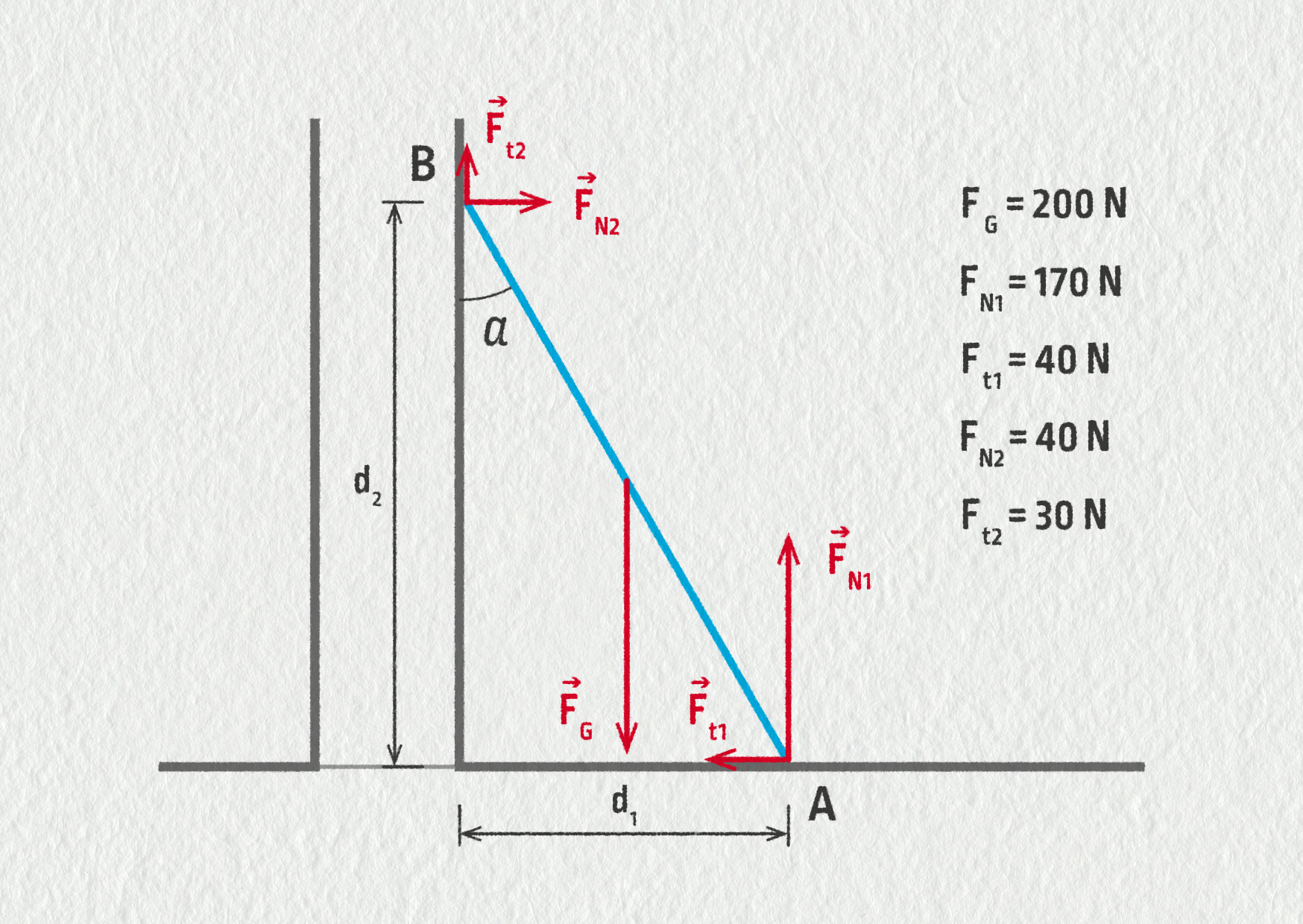
Zdroj
- Vypočítejte délky \(d_1\) a \(d_2\).
- Vypočítejte momenty všech sil vzhledem k ose procházející bodem A kolmo k nákresně. Kladný směr otáčení je proti směru hodinových ručiček.
- Je žebřík v rovnovážné poloze?
- 4,00 m; 6,93 m;
- vzhledem k bodu A: \(M_{\mathrm{t}1}=M_{\mathrm{N}1} = 0\), \(M_\mathrm{G}=+400\ \mathrm{N\cdot m}\), \(M_{\mathrm{t}2}=-120\ \mathrm{N\cdot m}\), \(M_{\mathrm{N}2}=-280\ \mathrm{N\cdot m}\);
- \(F_{\mathrm{t}1}\) se vyruší s \(F_{\mathrm{N}2}\), \(F_{\mathrm{t}2}\) a \(F_{\mathrm{N}1}\) se vyruší s \(F_\mathrm{G}\), součet momentů je nulový, podmínky rovnováhy jsou splněny
Cvičení 11
Dřevěný žebřík o délce 4 m a hmotnosti 30 kg je opřený o svislou zeď. Součinitel smykového tření mezi žebříkem a zemí a mezi žebříkem a zdí je 0,50. Vypočítejte maximální velikost úhlu, který může žebřík svírat se zdí, aniž by sklouzl, a velikosti všech sil působících na žebřík v této mezní situaci. Dosazujte hodnotu \(g=9{,}8\ \mathrm{m/s}^2\).
53,1°, při označení podle obrázku 16.47 je \(F_\mathrm{G}=294\ \mathrm{N}\), \(F_{\mathrm{N}1}=235\ \mathrm{N}\), \(F_{\mathrm{N}2}=F_{\mathrm{t}1}=118\ \mathrm{N}\), \(F_{\mathrm{t}2}=59\ \mathrm{N}\)

