Posuvný a otáčivý pohyb
Na obrázku je most architekta Václava Kociána a projektanta Davida Rose postavený v roce 2016 na železniční trati z Břeclavi do Vídně. Jedinečný svým designem i inženýrským řešením, pyšní se prvenstvím v celoevropské soutěži European Steel Bridge Awards. Bystrý pozorovatel zajisté ocení, jak dokonale stavba kopíruje linie okolní krajiny a jak se inženýři vypořádali s nepravoúhlým konceptem. Propočítat všechny tlaky a všechna napětí tak, aby jim odolaly namáhané součásti této důmyslné konstrukce, vyžaduje nemalou míru mistrovství a znalostí stavební mechaniky a nauky o vlastnostech materiálů. V této kapitole byste mimo jiné měli pochopit, jaké jsou ony základní fyzikální principy statiky staveb. Máte-li smysl pro hezké věci a současně hlavu na technická řešení, je stavebnictví dobrou volbou pro vaši profesní kariéru.
Posuvný a otáčivý pohyb
V předchozích kapitolách věnovaných mechanice jsme studovali situace, kdy tvar a rozměry tělesa nehrály podstatnou roli při jeho pohybu. Těleso jsme většinou bez dalšího vysvětlování nahradili hmotným bodem, vyšetřili, jaké síly na těleso působí, a pomocí Newtonových zákonů například předpověděli, jak se toto těleso bude pohybovat v budoucnosti. Toto zjednodušení lze provést jen v některých případech, jindy si s hmotným bodem nevystačíme.
V následujícím textu budeme předpokládat, že studované těleso má nezanedbatelné rozměry a že se jeho tvar, rozměry ani vnitřní rozložení hmoty nemohou měnit. Vytváříme tak zjednodušený model reality – model tuhého tělesa. Zjednodušení spočívá v tom, že síly působící na takové těleso mají pouze účinky pohybové, a nikoli deformační.
Ze všech možných druhů pohybů můžeme snadno popsat pohyb posuvný a pohyb otáčivý. Složitější pohyby je možné popsat jako složení pohybů posuvných a otáčivých.
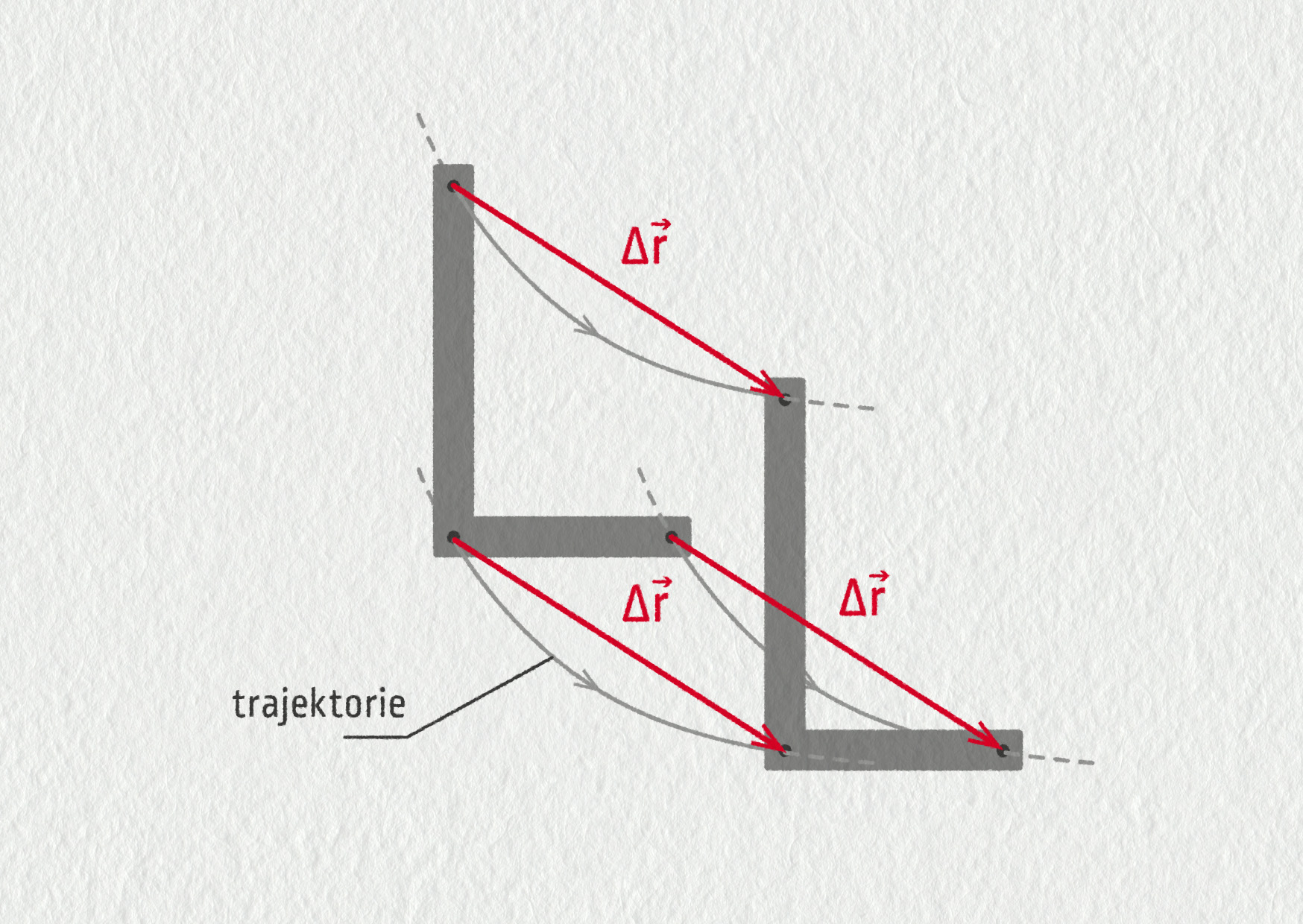
Posuvný pohyb neboli translace je charakteristický tím, že těžiště tělesa se v prostoru posouvá, ale těleso se při tom neotáčí. Znamená to, že za určitý čas \(\Delta t\) se všechny body tělesa (všechny části tělesa) posunou stejným směrem o stejnou vzdálenost. Lze tedy říci, že za čas \(\Delta t\) se všechny body tělesa posunou o stejný vektor \(\Delta\Vec{r}\). Při translaci mají v daný okamžik všechny body tělesa stejnou rychlost
\[ \Vec{v} = \frac{\Delta\Vec{r}}{\Delta t} \](velikost i směr) a pohybují se po trajektoriích stejného tvaru. Díky tomu můžeme v případě translace celé těleso nahradit jediným hmotným bodem a studovat pohyb jen tohoto hmotného bodu podle pravidel, která jsme se o pohybech dosud naučili. Posuvný pohyb vykonává např. konec prstu, kterým táhnete po displeji telefonu, řidič s autem na přímé silnici, píst ve spalovacím motoru atd.
Otáčivý pohyb neboli rotace se vyznačuje tím, že se těleso otáčí kolem určité osy, aniž se tato osa v prostoru nějak pohybuje. Osu otáčení budeme v našem výkladu značit písmenem \(z\). Za určitý čas \(\Delta t\) se všechny body tělesa (všechny části tělesa) otočí o stejný úhel \(\Delta\varphi\) kolem téže osy \(z\). To znamená, že všechny atomy mají v daný okamžik stejnou úhlovou rychlost
\[ \omega = \frac{\Delta\varphi}{\Delta t} \]
Na obrázku je vidět, že body tělesa se pohybují po soustředných kružnicích, jejichž středy leží na ose otáčení. Je také zřejmé, že při rotaci nemohou mít všechny části tělesa stejnou rychlost a že tato rychlost se zvětšuje spolu se vzdáleností od osy \(z\). Opíše-li totiž bod ve vzdálenosti \(r\) od osy otáčení oblouk o délce \(s\) za čas \(\Delta t\), bude velikost jeho rychlosti \(v=s/\Delta t=\Delta\varphi\cdot r/\Delta t=\omega r\). Pokud se těleso otáčí stálou úhlovou rychlostí, můžeme pro každý jeho bod používat vztahy platné pro rovnoměrný pohyb po kružnici. Otáčivý pohyb vykonává např. vrtule větrné elektrárny, řidič s autem na kruhovém objezdu, ručička na věžních hodinách atd.
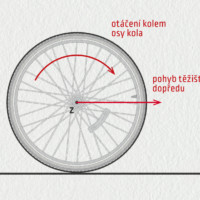
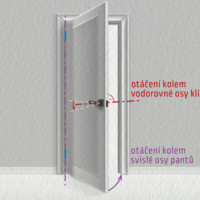
Složený pohyb vznikne, pokud předchozí pohyby probíhají současně. Složení translace a rotace můžeme pozorovat například u kola automobilu: kolo se otáčí kolem svojí osy a současně se tato osa posouvá ve směru jízdy. Složený pohyb vznikne i kombinací dvou rotací kolem dvou různých os, jako je tomu u kliky dveří: při zavírání dveří se klika i s dveřmi otáčí kolem svislé osy procházející panty, a pokud při tom kliku stiskneme, bude se současně otáčet i kolem vodorovné osy. Poznamenejme, že při skládání dvou translací má výsledný pohyb stále vlastnosti posuvného pohybu: parašutista klesající k zemi, jehož unáší boční vítr, se neotáčí, jeho tělo je stále ve svislé poloze.
Skládání pohybů
Kontrolní otázka
Prohlédněte si následující galerii a rozhodněte, jaký druh pohybu vykonávají vyfotografovaná tělesa. Do pole pro odpověď napište písmeno T v případě translace, R v případě rotace, nebo S v případě složeného pohybu.
[galerie title="Pohybující se tělesa"]
