Ověření zákona zachování mechanické energie
Úkol: Ověřte platnost zákona zachování mechanické energie pro kuličku valící se po nakloněné rovině.
Vybavení: deska k vytvoření nakloněné roviny, kulička, optická závora připojená k počítači a ovládací software, délkové měřidlo, posuvka
Mechanická energie \(E_\mathrm{m}\) je součet pohybové energie \(E_\mathrm{k}\) a polohové energie \(E_\mathrm{p}\) tělesa. Mechanická energie se zachovává, pokud na těleso nepůsobí nekonzervativní síly (třecí, tahové, …), nebo tyto síly nekonají práci. Zákon zachování energie je přírodním zákonem a podobně jako všechny přírodní zákony musí být ověřitelný experimentem.
K ověření zákona tedy musíme změřit kinetickou a potenciální energii kuličky v různých okamžicích pohybu po nakloněné rovině, a pokud bude vycházet jejich součet (v mezích chyb měření) stejný, mechanická energie se zachovává.
Zdroj
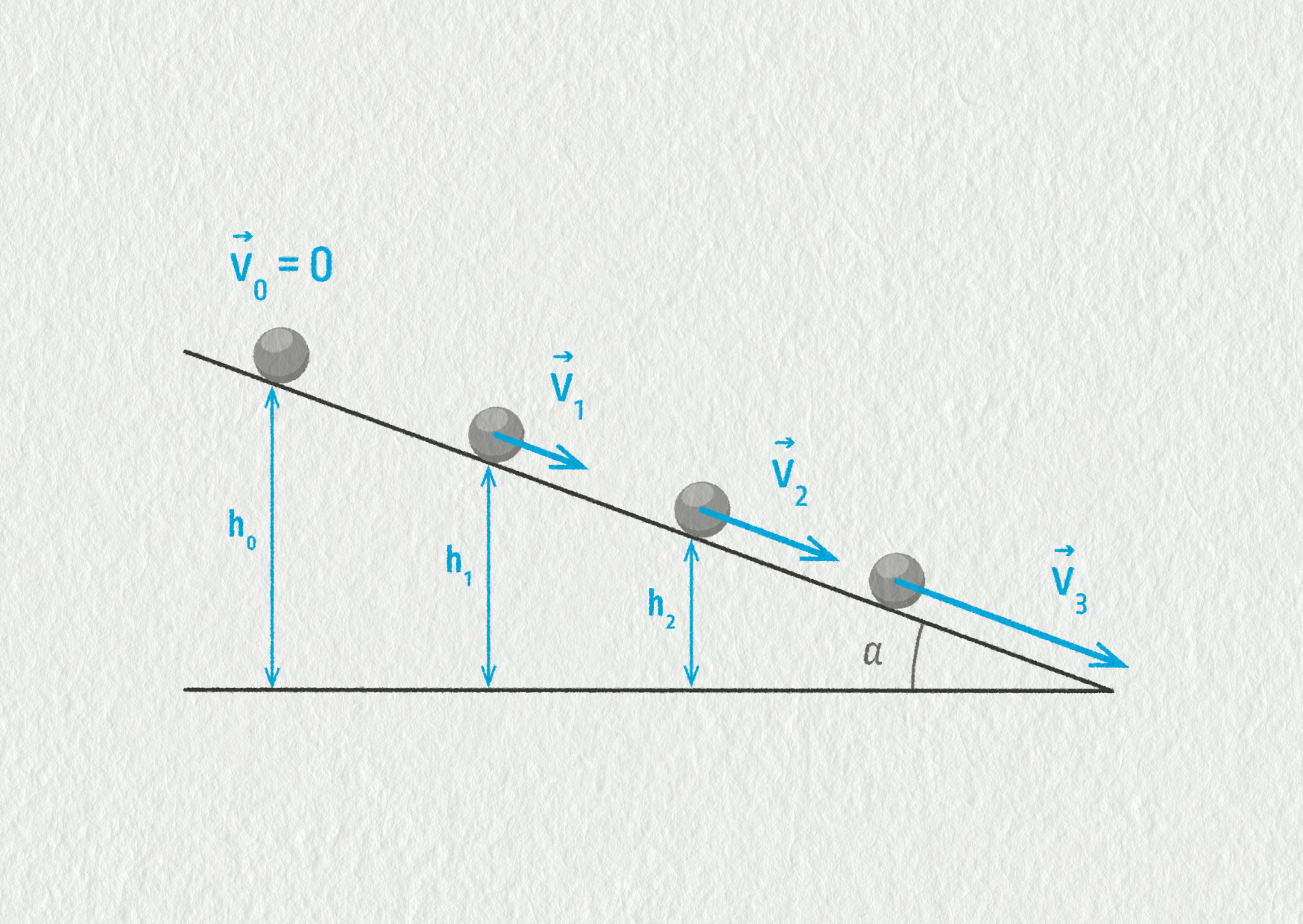
Kulička se nachází v gravitačním poli Země, její polohová energie je \(E_\mathrm{p}=mgh\), kde \(h\) je výška nad pevně zvolenou úrovní, např. rovinou pracovního stolu.
Kulička se po nakloněné rovině valí bez prokluzování, koná tedy složený pohyb z translace a rotace – oběma pohybům přísluší určitá kinetická energie.
K ověření zákona tedy musíme měřit okamžitou rychlost kuličky \(v\), právě když se nachází ve výšce \(h\). K tomu použijeme optickou závoru. Nastavíme ji tak, aby její světelný paprsek při průchodu mířil do středu kuličky. Kulička procházející optickou závorou tedy zakryje na velmi krátký čas \(t\) její světelný paprsek, přitom se odvalí o dráhu rovnou jejímu průměru. Měříme tedy dobu zakrytí paprsku \(t\) a počítáme okamžitou rychlost \(v\) jakožto průměr kuličky dělený \(t\).
Provedení:
- Změřte co nejpřesněji hmotnost \(m\) a průměr \(d\) kuličky.
- Vytvořte nakloněnou rovinu tak, aby se její sklon \(\alpha\) během experimentu neměnil.
- Pouštějte kuličku stále ze stejného místa a bez počáteční rychlosti a pomocí optické závory měřte její rychlost v různých výškách.
- Z naměřených dat vypočítejte energie \(E_\mathrm{p}\), \(E_\mathrm{kT}\), \(E_\mathrm{kR}\) a \(E_\mathrm{m}\).
- Sestrojte graf závislosti energií na výšce \(h\).
- Rozhodněte a zdůvodněte, zda provedené experimenty potvrdily platnost ZZME.
Ad 1) Doporučujeme použít kuličku kovovou nebo dřevěnou o průměru 2 až 4 cm. Nedoporučujeme používat kuličky měkké s velkým valivým odporem. Pokud použijete kuličku dutou, která má jiný moment setrvačnosti, je třeba opravit výpočet \(E_\mathrm{kR}\).
Ad 4) S posuvem těžiště kuličky je spojena kinetická energie \(E_\mathrm{kT}=\frac{1}{2}mv^2\), s jejím otáčením kinetická energie
\[ E_\mathrm{kR} = \frac{1}{2}J\omega^2 = \frac{1}{2}\left(\frac{2}{5}mr^2\right)\left(\frac{v}{r}\right)^2 = \frac{1}{5}mv^2 \]Ad 5) Pro kuličku o průměru 2,69 cm a hmotnosti 80,1 g můžeme při určitém sklonu nakloněné roviny získat tyto výsledky:
| \(h\ \mathrm{(cm)}\) | \(t\ \mathrm{(s)}\) | \(v\ \mathrm{(m/s)}\) | \(E_\mathrm{p}\ \mathrm{(J)}\) | \(E_\mathrm{kT}\ \mathrm{(J)}\) | \(E_\mathrm{kR}\ \mathrm{(J)}\) | \(E_\mathrm{m}\ \mathrm{(J)}\) |
|---|---|---|---|---|---|---|
| 12,3 | 0,054 | 0,496 | 0,0966 | 0,0099 | 0,0039 | 0,110 |
| 11,5 | 0,047 | 0,578 | 0,0903 | 0,0134 | 0,0054 | 0,109 |
| 9,3 | 0,040 | 0,674 | 0,0731 | 0,0182 | 0,0073 | 0,099 |
| 9,0 | 0,035 | 0,777 | 0,0707 | 0,0242 | 0,0097 | 0,105 |
| 7,2 | 0,030 | 0,903 | 0,0566 | 0,0326 | 0,0131 | 0,102 |
| 6,0 | 0,028 | 0,968 | 0,0471 | 0,0375 | 0,0150 | 0,100 |
Zdroj
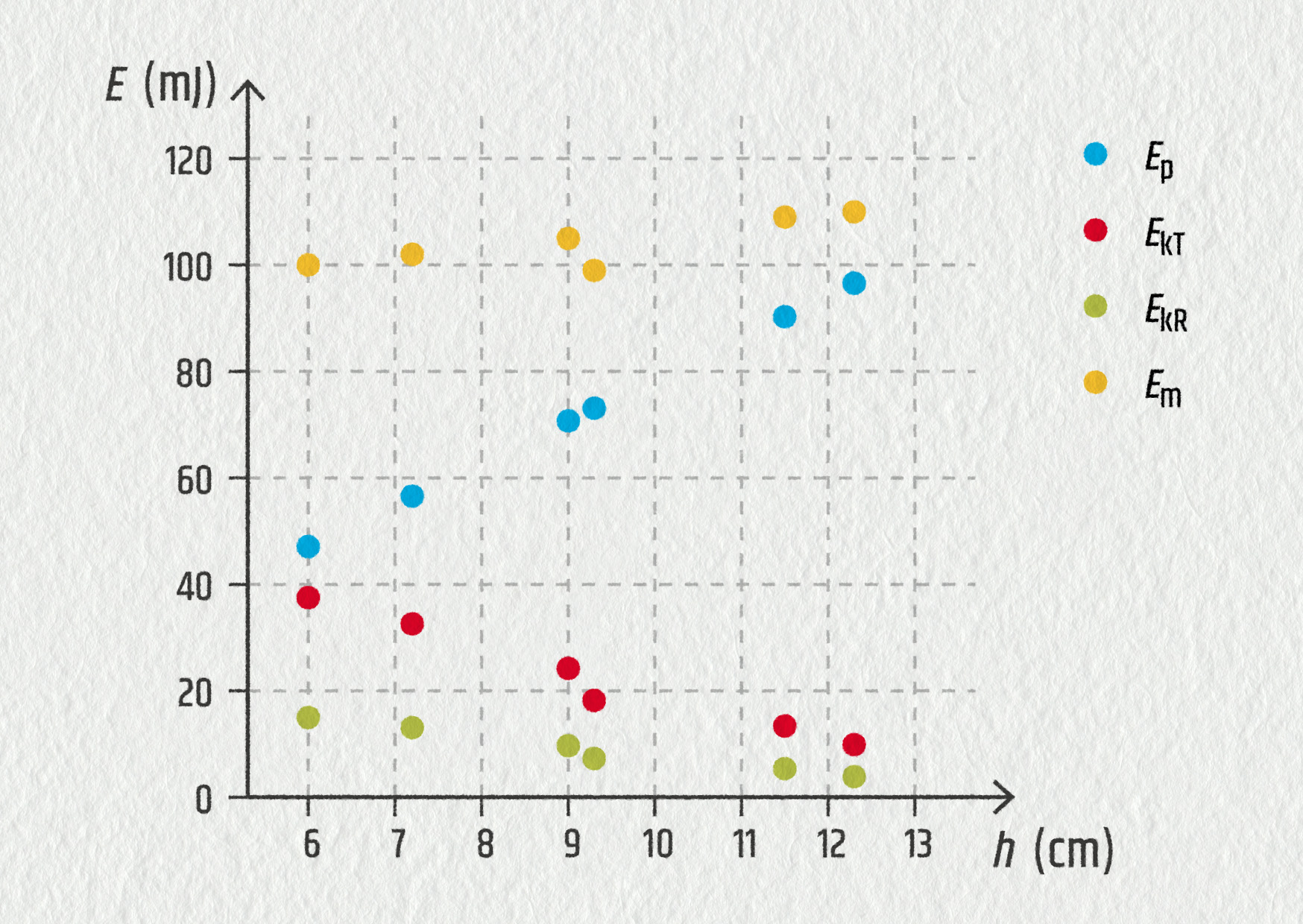
Ad 6) Vyhodnocení experimentu můžete ponechat na elementární úrovni: pokud hodnoty \(E_\mathrm{m}\) nezávisí na \(h\) a jen v důsledku náhodných chyb „poskakují“ kolem střední hodnoty, ZZME lze považovat za ověřený. Pokud naopak existuje korelace mezi \(E_\mathrm{m}\) a \(h\) (např. \(E_\mathrm{m}\) roste při zvyšování \(h\)), ZZME se ověřit nepodařilo.
S velmi šikovnou třídou lze vyhodnocení provést lépe: pokusit se odhadnout nejistotu měření podle pravidel vyložených v kapitole 2 a ověřit, zda se odchylka každé naměřené hodnoty \(E_\mathrm{m}\) od střední hodnoty \(E_\mathrm{m}\) liší méně, než činí nejistota měření.
Pro naše hodnoty je průměrná hodnota mechanické energie 0,104 J, maximální odchylka 0,006 J, což představuje 5,8 % z hodnoty \(E_\mathrm{m}\).
Odhad nejistot měření pro výšku \(h_4=9{,}0\ \mathrm{cm}\) a čas \(t_4=0{,}035\ \mathrm{s}\):
\(\Delta h=0{,}2\ \mathrm{cm}\), \(\delta h=2{,}2\,\%\) (pravítkem, optická závora není k nakloněné rovině pevně fixována)
\(\Delta t=0{,}002\ \mathrm{s}\), \(\delta t=5{,}7\,\%\) (vzorkovací frekvence 1000 Hz, odečítáme začátek a konec zakrytí)
\(\Delta m=0{,}1\ \mathrm{g}\), \(\delta m=0{,}1\,\%\) (citlivost digitální váhy)
\(\Delta d=0{,}4\ \mathrm{cm}\), \(\delta d=14{,}9\ \%\) (odhad, paprsek optické závory má šířku 2 mm, uvažujeme zakrývání a odkrývání)
Nejistotu tíhového zrychlení \(g=9{,}8065\ \mathrm{m/s^2}\) nemusíme uvažovat.
\(\delta v=16{,}0\,\%\)
\(\delta E_\mathrm{p}=2{,}2\,\%\), \(\Delta E_\mathrm{p}=1{,}6\ \mathrm{mJ}\)
\(\delta E_\mathrm{kT}=22{,}6\,\%\), \(\Delta E_\mathrm{kT}=5{,}5\ \mathrm{mJ}\)
\(\delta E_\mathrm{kR}=22{,}6\,\%\), \(\Delta E_\mathrm{kR}=2{,}2\ \mathrm{mJ}\)
Nejistota určení mechanické energie je \(\Delta E_\mathrm{m}=6{,}1\ \mathrm{mJ}=0{,}0061\ \mathrm{J}\)
Nejistota měření je stejná jako maximální odchylka naměřené mechanické energie od střední hodnoty. Zákon zachování se v mezích nejistot měření podařilo ověřit.
Často se u žáků setkáváme s hrubě nesprávným vysvětlením, že se mechanická energie při valení kuličky na nakloněné rovině zachovává, protože je třecí síla zanedbatelná. Toto je velmi rozšířený mýtus plynoucí z nepochopení situace.
Ve skutečnosti je třecí síla přítomna a ovlivňuje pohyb kuličky.
Kdyby byla třecí síla nulová nebo zanedbatelná, kulička by se vůbec neroztočila a po nakloněné rovině by klouzala jako sáňky po svahu. Tím pádem by v každé výšce musela mít větší rychlost, než reálně má, protože část její kinetické energie je v reálu „uložena“ právě do otáčivého pohybu. (*)
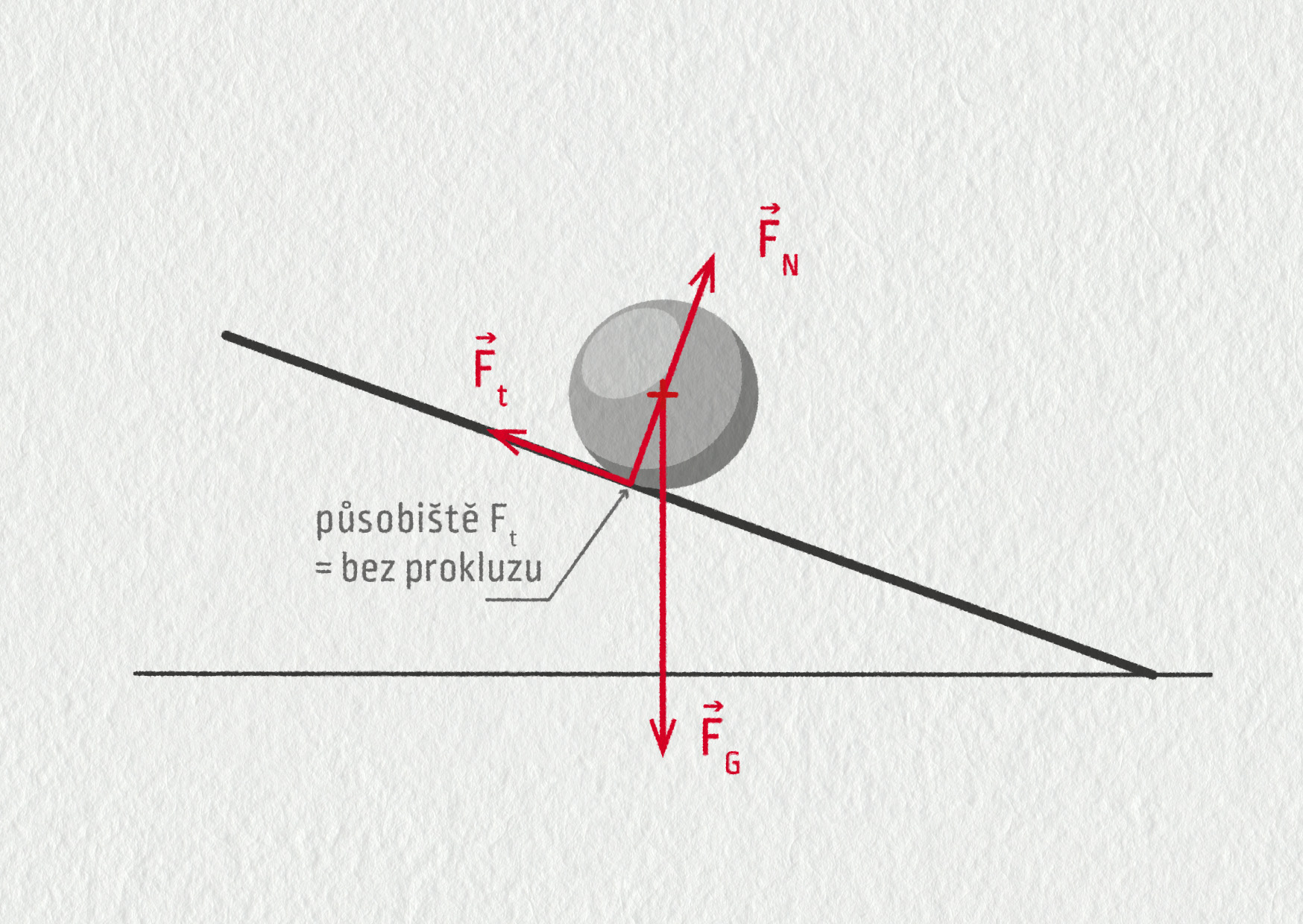
Zdroj
Skutečný stav vidíte na obrázku. Třecí síla působí v bodě dotyku kuličky a podložky rovnoběžně s podložkou. Na rozdíl od \(\Vec{F}_\mathrm{G}\) a \(\Vec{F}_\mathrm{N}\) je její moment vůči těžišti kuličky nenulový, takže právě třecí síla je zodpovědná za to, že se kulička roztočí kolem osy procházející těžištěm.
Síla třecí \(\Vec{F}_\mathrm{t}\) podobně jako síla normálová \(\Vec{F}_\mathrm{N}\) jsou nekonzervativní. Jenže kulička po podložce neprokluzuje, což znamená, že působiště třecí ani normálové síly se v žádný okamžik nepohybuje. Proto tyto dvě nekonzervativní a nenulové síly nekonají práci.
Můžeme tedy uzavřít, že třecí síla vůbec není zanedbatelná, ale v případě valení bez prokluzu nekoná práci, takže se mechanická energie zachovává.
(*) O tom, že k nepochopení situace může dojít i mezi učiteli a může se dokonce dostat i do učebnic, vtipně referuje Richard Feynman v knize To snad nemyslíte vážně, pane Feynmane! – viz pasáž o výuce fyziky v Brazílii. 🙂

