Atomová hypotéza
V této kapitole začneme podrobněji zkoumat, jaká je vnitřní struktura různých látek a jaké to má důsledky. Základem našich představ je existence atomů a molekul – atomová hypotéza. Tento nápad je starý víc jak dvě tisíciletí; pochází od řeckého filosofa Démokrita z Abdér. Démokritos uvažoval o tom, že hmotu nelze donekonečna dělit na menší a menší části, proto musí existovat nějaké základní stavební částice – atomy. Jenže tyhle atomy jsou tak malé, že není možné je pozorovat přímo lidským zrakem ani optickým mikroskopem. Proto se z atomové hypotézy stal experimentálně prokázaný fakt až počátkem 20. století (více o tom najdete v motivační aktivitě „Je možné pozorovat atomy?“). V dnešní době můžeme atomy pozorovat prostřednictvím speciálních mikroskopů, např. AFM (atomic force microscopy). S atomy můžeme dokonce manipulovat; poprvé se to povedlo v roce 1989 vědcům z laboratoří IBM, kteří z pouhých 35 atomů xenonu vytvořili miniaturní logo (viz obrázek).

Zdroj
Co víme o atomech dnes? To nejdůležitější lze shrnout do čtyř jednoduchých vět.
- Atomy se neustále chaoticky pohybují.
- Atomy na sebe působí elektrickými silami.
- Atomy jsou velmi malé, řádově 0,1 nm.
- Atomy se mohou spojovat do molekul.
V celé kapitole budeme z těchto poznatků vycházet. Pro většinu fyzikálních úvah není podstatné, zda se jedná o atom či molekulu, jejich chování je totiž podobné. Pro začátek si představte obyčejnou sklenici vody. Na první pohled voda vypadá docela klidně, ale ve skutečnosti se všechny její molekuly neustále divoce pohybují a s tím je spojena docela velká kinetická energie. Tuto vnitřní kinetickou energii můžeme zvýšit tím, že vodu ohřejeme. Rychlost pohybu molekul souvisí s teplotou. O tom se můžeme přesvědčit jednoduchým pokusem. K naší sklenici přidáme ještě druhou, do které nalijeme vodu horkou. Po ustálení víření vody do obou sklenic kápneme barvivo. Můžeme sledovat, jak se molekuly barviva postupně promíchávají s molekulami vody. Tento jev se nazývá difúze a jeho rychlost závisí na teplotě, neboť s teplotou roste rychlost chaotického pohybu molekul.

Zdroj
Molekuly vody se pohybují, ale voda ve sklenici přesto zůstává s jasně ohraničenou hladinou. Je to tím, že mezi molekulami vody působí přitažlivé síly. Přesto se na hladině občas najde molekula, které se přitažlivou sílu překonat podaří a od zbytku vody se odpoutá. Pozorujeme to jako vypařování vody (asi vás nepřekvapí, že horká voda se bude vypařovat rychleji). Síly, kterými na sebe působí atomy a molekuly, nazýváme obecně vazebné síly. S tím je spojená také potenciální vazebná energie. Není to ale tak jednoduché; problematika vzájemného působení atomů a molekul je velmi složitá a je základem celé chemie.
Podívejme se do třetice na naši sklenici vody. Kolik molekul vody obsahuje? V dalším textu se to naučíte sami spočítat, ale pojďme si teď prozradit výsledek a zamyslet se nad ním. 3 dl vody obsahují asi 1025 molekul. Proti tomu je 300 miliard hvězd v naší galaxii opravdu směšně malé číslo. Následující úloha vám pomůže lépe si představit takto obrovské množství.
- Představte si, že by se každou sekundu ze sklenice vody (= 1025 molekul) vypařilo 300 miliard molekul. Za jak dlouho by všechna voda zmizela?
- Představte si, že 3 dl vody ze sklenice nalijete do oceánu a dokonale promícháte. Voda ze všech světových oceánů má objem asi 1,3 ⋅ 1018 m3. Pak naberete stejnou sklenici vody z oceánu. Budou v ní nějaké molekuly z vaší původní sklenice? A případně kolik?
a) Je to jednoduché:
\[t=\frac{10^{25}}{300\cdot10^9}\ \mathrm{s}=3{,}3\cdot10^{13}\ \mathrm{s}\approx10^{6}\ \mathrm{let}\]To znamená, že ve skutečnosti se každou sekundu vypaří mnohem víc než 300 miliard molekul!
b) Poměr ředění je
\[\frac{0{,}0003\ \mathrm{m}^3}{1,3\cdot10^{18}\ \mathrm{m}^3}=2{,}3\cdot10^{-22}\]Počet molekul ve sklenici je ale 1025, takže po zředění jich bude \(2{,}3\cdot10^{-22}\times10^{25}=2300\).
Voda se může vypařit nebo zmrznout, což lze opět snadno pochopit na úrovni atomů a molekul. Přehledně to shrnuje obrázek tří skupenství látky.
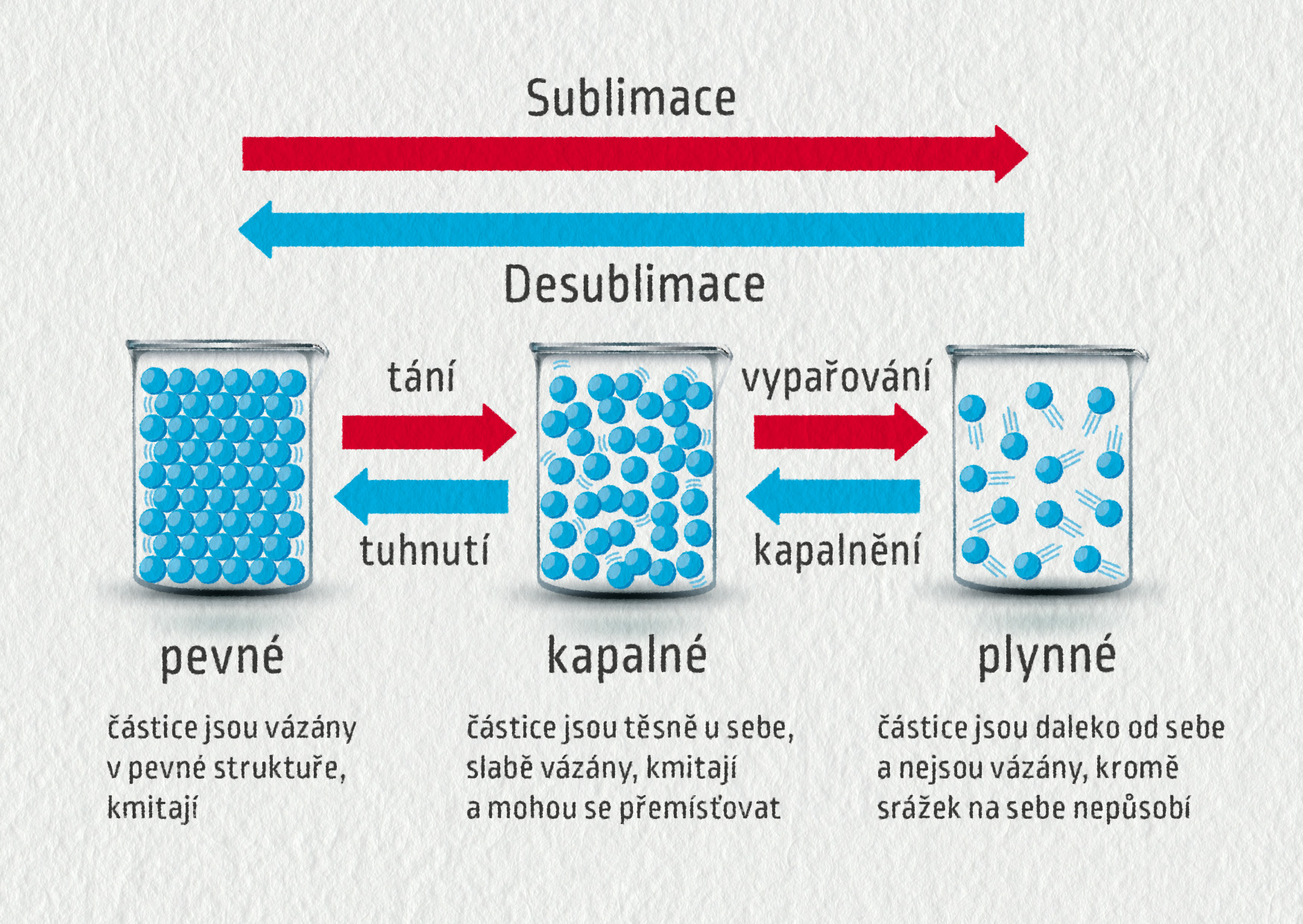
Zdroj
Jak počítáme množství částic v tělese?
Atom je velmi malá částice, takže bychom ho samotný těžko zvážili. Nejlehčí atom vodíku má hmotnost pouhých 1,67 ⋅ 10−27 kg. Lepší představu o vzájemné hmotnosti atomů proto získáme, když určíme, kolikrát je nějaký atom těžší než atom vodíku. Například atom helia je zhruba čtyřikrát těžší než atom vodíku, proto bychom mohli říct, že jeho relativní atomová hmotnost je 4. Z praktických důvodu se místo atomu vodíku používá atomová hmotnostní konstanta u, číselně blízká hmotnosti atomu vodíku.
Relativní atomová hmotnost \(A_\mathrm{r}=m_\mathrm{a}/\mathrm{u}\)
\(\mathrm{u} = 1{,}660\,539\cdot10^{-27}\ \mathrm{kg}\) (atomová hmotnostní konstanta)
\(m_\mathrm{a}\) = hmotnost atomu
Obdobně můžeme definovat také relativní molekulovou hmotnost \(M_\mathrm{r}=m_\mathrm{m}/\mathrm{u}\), kde \(m_\mathrm{m}\) je hmotnost molekuly. Podívejme se nyní na příklady relativních hmotností různých látek. Přesné hodnoty pro všechny prvky najdete například zde: https://cs.wikipedia.org/wiki/Rozšířená_periodická_tabulka
| Značka | Název | \(A_\mathrm{r}\) (\(M_\mathrm{r}\)) |
|---|---|---|
| H | vodík | 1,008 |
| He | helium | 4,003 |
| Li | lithium | 6,941 |
| C | uhlík | 12,011 |
| O | kyslík | 15,999 |
| Fe | železo | 55,845 |
| H2 | molekulární vodík | 2,016 |
| H2O | voda | 18,015 |
| N2 | molekulární dusík | 28,014 |
Zaokrouhlené hodnoty relativních hmotností vyplývají ze složení atomů (molekul). Tak například jádro helia se skládá ze dvou protonů a dvou neutronů, proto \(A_\mathrm{r}=4\). Podobně uhlík je šestý prvek periodické tabulky, má 6 protonů a 6 neutronů, proto \(A_\mathrm{r}=12\). Pozor, nejde o pravidlo, u těžších prvků už převažují neutrony nad protony. Například železo má 26 protonů a 30 neutronů, proto \(A_\mathrm{r}=56\). Velmi dobře se dají odvodit i hmotnosti molekul. Třeba takový vodík ve formě dvouatomové molekuly H2 má \(M_\mathrm{r}=2\). Molekula H2O se skládá ze dvou vodíků a jednoho kyslíku, proto \(M_\mathrm{r}=2+16=18\).
Proč nejsou ve skutečnosti relativní atomové hmotnosti celá čísla? Důvody jsou dva a oba velmi zajímavé.
- Prvky se v přírodě obvykle vyskytují jako směs izotopů (atomů se stejným počtem protonů a různým počtem neutronů). Prvek je v přírodě tvořen směsí atomů o různé hmotnosti. Silně se to projeví například u lithia, kde dominuje těžší izotop 7Li. Naopak minimální vliv je u vodíku, kde 99,985% představuje izotop 1H.
- V jádru se uplatňují relativistické efekty – hmotnost jádra je menší než hmotnost oddělených protonů a neutronů, konkrétně platí rovnice spojující hmotnost s energií \(E=mc^2\) (podrobněji v kapitole 27).
Jaká je přibližně relativní molekulová hmotnost oxidu uhličitého (CO2)?
\(M_\mathrm{r}={}\) [...]
Pomocí relativní atomové hmotnosti můžeme snadno počítat hmotnosti atomů (molekul), ale také množství atomů (molekul) v určitém množství látky, neboť pro celkovou hmotnost tělesa m musí platit \(m=Nm_\mathrm{a}\), kde \(N\) je počet atomů (molekul), \(m_\mathrm{a}\) je hmotnost jednoho atomu (molekuly).
Množství atomů v běžných tělesech dokážeme zapsat jen pomocí obrovských čísel. Proto byla zavedena speciální fyzikální veličina látkové množství s jednotkou mol. Jeden mol není nic jiného než přesně určený „balíček“ částic. Počet částic v tomto „balíčku“ je určen Avogadrovou konstantou \(N_\mathrm{A}=6{,}022\,140\,76\cdot10^{23}\ \mathrm{mol}^{-1}\).
Látkové množství \(n = N / N_\mathrm{A}\)
\(N_\mathrm{A}=6{,}022\,140\,76\cdot10^{23}\ \mathrm{mol}^{-1}\) (Avogadrova konstanta)

Zdroj
- Vypočítejte hmotnost jedné molekuly vody.
- Vypočítejte počet molekul v 0,3 kg vody.
- Vypočítejte látkové množství 0,3 kg vody.
a) \(m_\mathrm{m} = M_\mathrm{r}u = 18\times1{,}66\cdot10^{-27}\ \mathrm{kg} = 30\cdot10^{-27}\ \mathrm{kg}\).
b) \(\displaystyle N=\frac{m}{m_\mathrm{m}} = \frac{0{,}3\ \mathrm{kg}}{30\cdot10^{-27}\ \mathrm{kg}} = 10^{25}\).
c) \(\displaystyle n=\frac{N}{N_\mathrm{A}} = \frac{10^{25}}{6\cdot10^{23}\ \mathrm{mol}^{-1}} = 17\ \mathrm{mol}\).
Vypočítejte hmotnost jednoho molu
- atomárního vodíku (H),
- železa (Fe),
- vody (H2O).
Máme provést ten samý výpočet třikrát, jen pokaždé pro jinou látku. Určitě se proto vyplatí začít obecným řešením a dosazování číselných hodnot nechat až nakonec. Platí
\[ \begin{aligned} m &=Nm_\mathrm{a}\\ &=nN_\mathrm{A}m_\mathrm{a}\\ &=nN_\mathrm{A}A_\mathrm{r}u\\ \end{aligned} \]V našem případě je látkové množství \(n = 1\ \mathrm{mol}\) a součin Avogadrovy konstanty a atomové hmotnostní konstanty je
\[ N_\mathrm{A}u = 6{,}022\cdot10^{23}\ \mathrm{mol}^{-1} \times 1{,}66\cdot10^{-27}\ \mathrm{kg} = 0,001\ \mathrm{kg}\cdot\mathrm{mol}^{-1} \]Teď jsme připraveni dosazovat
- \(m = 1\ \mathrm{mol}\times0{,}001\ \mathrm{kg}\cdot\mathrm{mol}^{-1}\times 1 = 0{,}001\ \mathrm{kg}=1\ \mathrm{g}\).
- \(m = 1\ \mathrm{mol}\times0{,}001\ \mathrm{kg}\cdot\mathrm{mol}^{-1}\times 56 = 0{,}001\ \mathrm{kg}=56\ \mathrm{g}\).
- \(m = 1\ \mathrm{mol}\times0{,}001\ \mathrm{kg}\cdot\mathrm{mol}^{-1}\times 18 = 0{,}001\ \mathrm{kg}=18\ \mathrm{g}\).
Systematický postup se nám vyplatil! Vidíme, že výpočty pro konkrétní látky jsou po obecném odvození již velmi jednoduché. Dokonce jsme dokázali, že hmotnost jednoho molu v gramech je číselně rovna relativní atomové (molekulové) hmotnosti.
V předchozím příkladu jsme odhalili zajímavou souvislost: molární hmotnost = hmotnost jednoho molu v gramech – je číselně rovna relativní atomové (molekulové) hmotnosti. To je možné jen díky tomu, že součin Avogadrovy konstanty a atomové hmotnostní konstanty je roven \(0{,}001\ \mathrm{kg}\cdot\mathrm{mol}^{-1} = 1\ \mathrm{g}\cdot\mathrm{mol}^{-1}\). Jinými slovy, hmotnost 1 molu vodíku je přibližně 1 g. Avogadrova konstanta je zvolena právě tak, aby hmotnost 1 molu uhlíku 12C byla přesně 12 g. Molární hmotnost je v praxi často používanou veličinou, proto si zaslouží vlastní definici:
Molární hmotnost \(M_\mathrm{m}=m/n\)
\(n\) je látkové množství, \(m\) je hmotnost látky.
Všechny veličiny přehledně shrnuje závěrečná grafika:
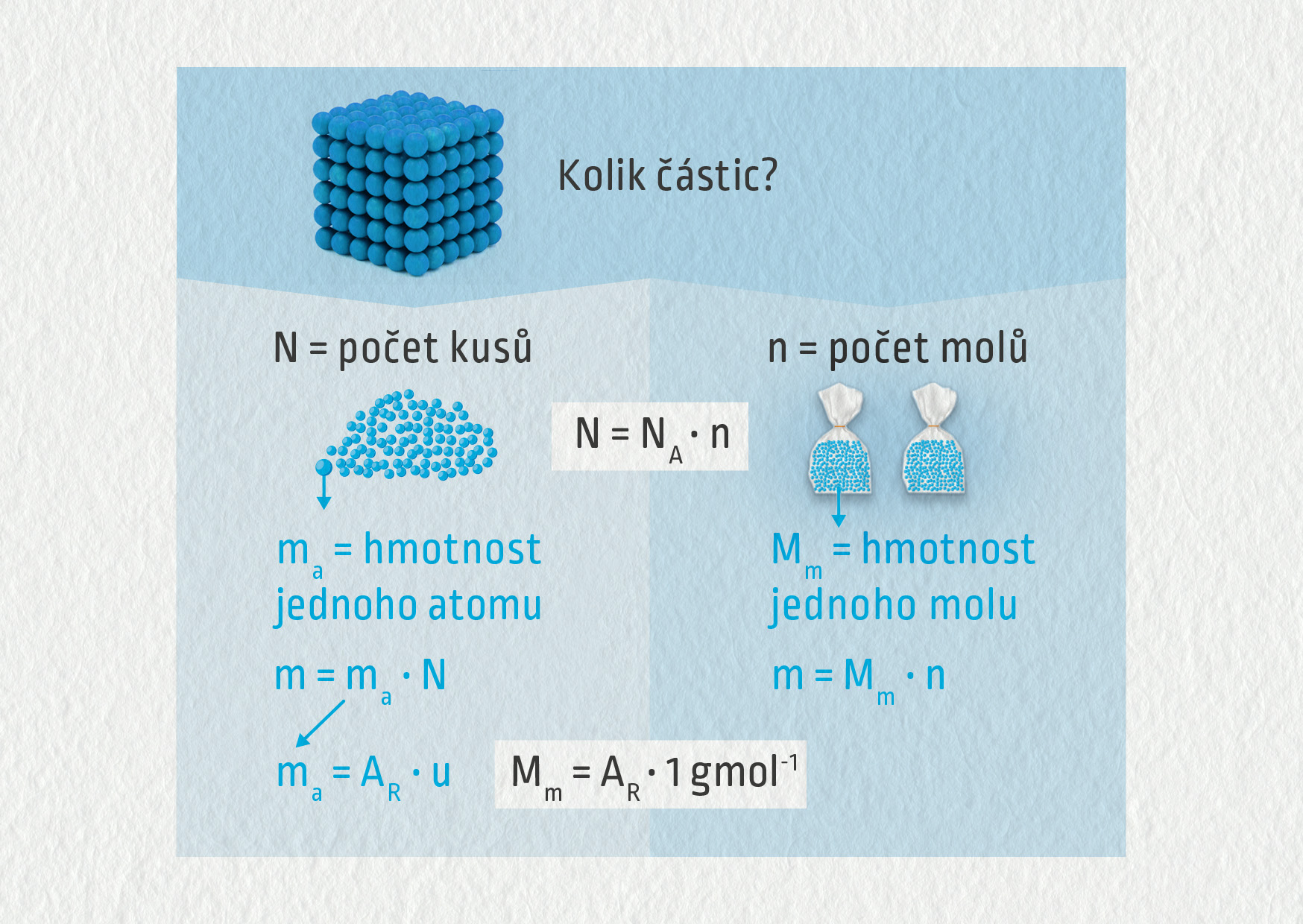
Zdroj
- Kolik kg CO2 vznikne spálením 1 kg čistého uhlíku?
- V zemské atmosféře je asi 2 ⋅ 1015 kg oxidu uhličitého. Lidé ročně spálí asi 6 ⋅ 1012 kg uhlíku z fosilních paliv. Jaký je roční přírůstek oxidu uhličitého za předpokladu, že veškerý oxid uhličitý je zachován v atmosféře?
a) Nezáleží na přesném průběhu chemických reakcí. Podstatné jsou vstupy a výstupy, v tomto případě tedy můžeme zapsat
\[ \mathrm{C}+\mathrm{O_2}\to\mathrm{CO_2} \]Pro relativní hmotnosti platí: \(A_\mathrm{R}(\mathrm{C})=12\), \(M_\mathrm{R}(\mathrm{O}_2)=32\), \(M_\mathrm{R}(\mathrm{CO}_2)=12+32=44\). Můžeme tedy říci, že poměr hmotností \(M_\mathrm{R}(\mathrm{CO}_2)/A_\mathrm{R}(\mathrm{C})=44/12=11/3=3,7\). Z toho vyplývá, že spálením 1 kg uhlíku vznikne asi 3,7 kg CO2.
b) Díky předchozímu výpočtu už stačí jen násobit \(3,7\times6\cdot10^{12}\ \mathrm{kg} = 22\cdot10^{12}\ \mathrm{kg} = 2\cdot10^{12}\ \mathrm{kg}\). To je asi 1 % celkového množství v atmosféře.
I když molekuly a atomy nejsou pouhým okem viditelné, vědcům se přesto podařilo je změřit i spočítat. K tomu však vedla dlouhá a klikatá cesta. Jedním z těch, kdo se o to zasloužil, byl italský šlechtic Lorenzo Romano Amedeo Carlo Avogadro, hrabě z Quarenga a Cerreta. V roce 1811 publikoval hypotézu o tom, že počet částic plynu je za stejného tlaku a teploty přímo úměrný objemu plynu. Tento předpoklad vystavěl na domněnce, že hmotnost molekul je přímo úměrná hustotě plynu. Základní myšlenka jeho teorie vycházela z představy, že nejmenší částice plynu jsou molekuly (molekula – latinsky malé množství hmoty), které jsou složeny ze dvou nebo i více atomů. Za svého života se Amedeo Avogadro potvrzení a uznání své molekulární hypotézy nedočkal – mezi současníky nevzbudila téměř žádnou pozornost, a pokud ano, byla i odmítána. Avogadro totiž nedokázal své hypotézy přesně experimentálně ověřit.
Prvním vědcem, který dokázal molekuly skutečně „spočítat“, byl Rakušan českého původu Johann Josef Loschmidt. V roce 1866 publikoval práci „O velikosti molekul vzduchu“. Loschmidt určil rozměry molekul tak, že porovnával hustotu látky v kapalném a plynném skupenství. Předpokládal přitom, že molekuly jsou kulovitého tvaru a v kapalném skupenství jsou k sobě těsně uspořádány. Na základě svých výpočtů určil počet molekul v 1 cm3 ideálního plynu při normálním tlaku a teplotě. Ten je dnes označován jako Loschmidtova konstanta.
Samotný pojem „Avogadrova konstanta“ pak vytvořil v roce 1909 fyzik Jean Perrin, který ji definoval jako počet molekul v přesně 32 gramech kyslíku. Cílem této definice bylo dosáhnout toho, aby se hmotnost molu látky v gramech číselně rovnala relativní molekulové hmotnosti jeho molekul.

Zdroj
V roce 1971 bylo látkové množství určeno jako nezávislá fyzikální veličina a mol jako jedna ze sedmi základních jednotek soustavy SI. Konkrétně byl mol definován jako množství látky, která obsahuje tolik částic, kolik je atomů ve 12 g uhlíku 12C. V důsledku této definice získala Avogadrova konstanta v systému SI hodnotu přibližně \(6{,}022\cdot10^{23}\ \mathrm{mol}^{-1}\). Od roku 2019 je pak Avogadrova konstanta pevně stanovená jako \(N_\mathrm{A} = 6{,}022\,140\,76\cdot10^{23}\ \mathrm{mol}^{-1}\).
Hodnotu Avogadrovy konstanty je možné velmi přesně změřit například pomocí zkoumání struktury pravidelných krystalů nebo pomocí elektrolýzy (tuto metodu si můžete sami vyzkoušet v praktiku).

