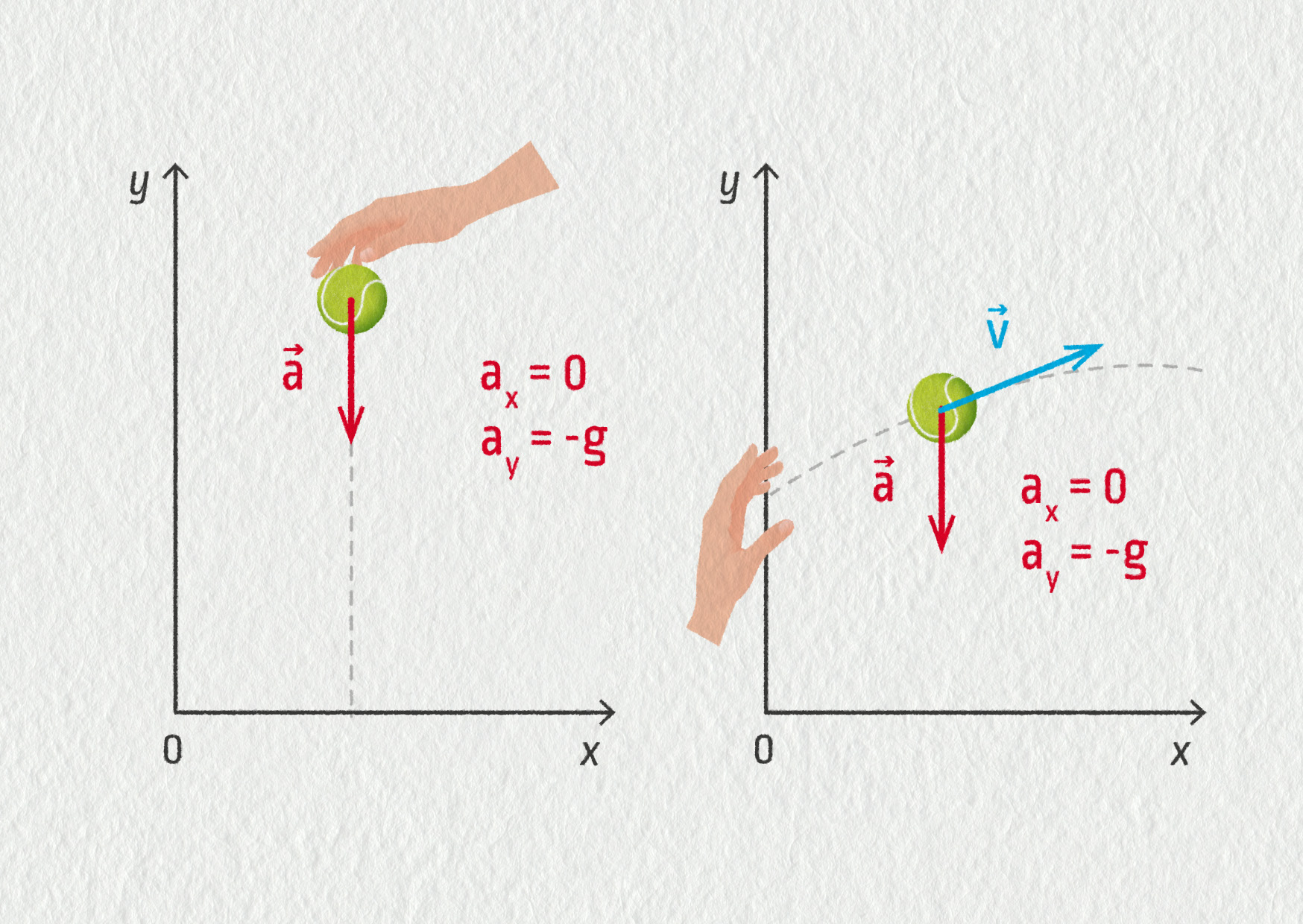
Ocitneme se v trochu jiné situaci, když budeme studovat vrhy. O vrzích hovoříme, jestliže nás zajímá pohyb tělesa v homogenním tíhovém poli Země. Předpokládáme, že na těleso působí pouze tíhová síla. Odpor vzduchu tedy zanedbáváme. Můžeme rozlišit, zda je tělesu udělena počáteční rychlost a jaký má směr. Podle toho rozlišíme volné pády (nulová počáteční rychlost) a vrhy svislé, vodorovné či šikmé. Vrhy svislý, vodorovný a šikmý se liší právě směrem počáteční rychlosti.
Zdroj
Ať už jde o volný pád nebo vrh, zrychlení tělesa je stejné. Na těleso působí pouze tíhová síla, která je svislá a míří dolů. Podle druhého Newtonova zákona je zrychlení tělesa orientováno stejně jako výsledná síla, v tomto případě tíhová síla. Můžeme tedy zrychlení zapsat ve tvaru \(\Vec{a}=(0,-g)\), pokud jsou osy souřadnicového systému vodorovná a svislá.
Na dva vrhy se podívejme detailněji v následujících řešených příkladech.
Vrh vodorovný
V případě vodorovného vrhu má počáteční rychlost vodorovný směr. Jaké to má důsledky pro pohyb tělesa? Bude jeho trajektorií přímka? Kam dopadne a za jak dlouho? Jakou rychlostí?
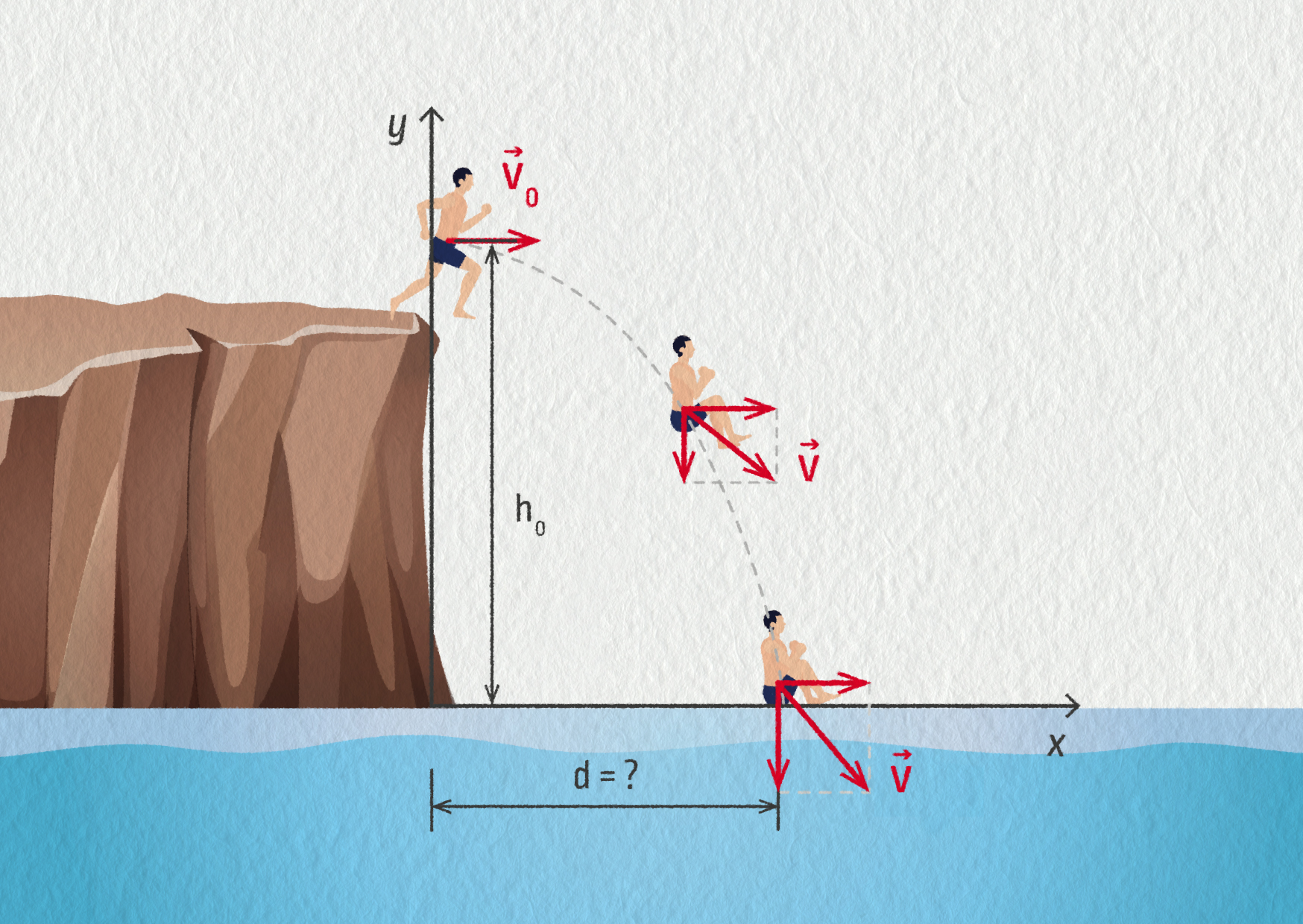
Chlapec na obrázku skáče do vody v jezeře z břehu, který je 2,4 m nad hladinou jezera. Jak daleko od břehu dopadne, když se rozběhne rychlostí \(v_0=2{,}6\ \mathrm{m/s}\) a jeho těžiště je ve výšce 80 cm nad úrovní břehu? (Viz obrázek 15.16.)
Zdroj
Zvolme nejprve soustavu souřadnic a určeme počáteční podmínky pohybu chlapce. V okamžiku odrazu, tedy v čase \(t=0\ \mathrm{s}\), se nachází v bodě, jehož polohu určuje svislý vektor \(\Vec{r}_0=(0,h_0)\). Má také vodorovnou rychlost \(\Vec{v}=(v_0,0)\). Na chlapce působí pouze tíhová síla, ostatní síly zanedbáváme. Součet všech působích sil je roven pouze tíhové síle a podle druhého Newtonova zákona tedy můžeme napsat \(\Vec{F}=m\Vec{g}=m\Vec{a}\). Pro zrychlení tedy získáme složky \(\Vec{a}=(0,-g)\). Proto můžeme sestavit časové rovnice ve tvaru
\[ \begin{aligned} v_x(t) &= v_0\\ v_y(t) &= -gt\\ \end{aligned} \]a
\[ \begin{aligned} x(t) &= v_0t\\ y(t) &= -\frac12gt^2+h_0\\ \end{aligned} \]Co tyto rovnice pro pohyb znamenají? Nenulové složky rychlosti nás informují o tom, že probíhá pohyb ve směru osy \(x\) i osy \(y\). Ve směru osy \(x\) se ale rychlost nemění, můžeme se tedy na tuto část pohybu dívat jako na pohyb rovnoměrný. Rovnice pro polohu \(x\) tomuto závěru zcela odpovídá.
Ve směru osy \(y\), kde pohyb původně neprobíhal, dochází k nárůstu rychlosti ve směru dolů – těleso padá, znaménko této složky je záporné. Pohyb v tomto směru je rovnoměrně zrychlený, což opět potvrzujeme v rovnici pro výšku tělesa nad hladinou vody.
Abychom určili, jak daleko chlapec dopadne, musíme nejprve vypočítat dobu jeho pohybu vzduchem. V místě dopadu na hladinu je jeho výška nulová, píšeme tedy
\[ y(t_\mathrm{D}) = 0 = -\frac12gt^2+h_0\;. \]Pro dobu pádu platí
\[ t_\mathrm{D}=\sqrt{\frac{2h_0}h}=\sqrt{\frac{2\cdot3{,}2}{9{,}81}}\ \mathrm{s}=0{,}81\ \mathrm{s}\;. \]Tento čas poté dosadíme do vztahu pro x-ovou souřadnici, která je v místě dopadu rovna právě hledané vzdálenosti \(d\):
\[ d=x(t_\mathrm{D})=v_0t_\mathrm{D}=2{,6}\cdot0{,}81\ \mathrm{m}=2{,}1\ \mathrm{m}\;. \]Zajímá-li nás otázka, s jakou rychlostí chlapec do vody dopadne, musíme z času \(t_\mathrm{D}=0,81\ \mathrm{s}\) určit obě složky rychlosti \(v_{\mathrm{D}x}=v_0=2{,}6\ \mathrm{m/s}\) a \(v_{\mathrm{D}y}=-gt=-9{,}81\cdot0{,}81=-7,9\ \mathrm{m/s}\). Pro velikost rychlosti tedy platí
\[ v_\mathrm{D}=\sqrt{v_{\mathrm{D}x}^2+v_{\mathrm{D}y}^2}=\sqrt{2{,}6^2+(-7{,}9)^2}=8{,}3\ \mathrm{m/s}\;. \]Vrh vodorovný můžeme popsat jako pohyb rovnoměrný ve směru osy \(x\) a pohyb rovnoměrně zrychlený ve směru osy \(y\). Počáteční rychlost směřuje pouze ve vodorovném směru (osa \(x\)), zatímco zrychlení je svislé. Proto se rychlost ve směru této osy nebude měnit. Ve směru svislém (osa \(y\)) jde o volný pád bez počáteční rychlosti. Složka rychlosti ve směru osy \(y\) narůstá přímo úměrně času.
Trajektorií vodorovného vrhu je křivka, protože dochází k pohybu v obou směrech. Určeme nyní její rovnici. Matematicky jde o funkci \(y=f(x)\). Proto z rovnice \(x(t)=v_0t\) vyjádříme čas \(t=x/v_0\) a dosadíme do rovnice pro \(y\). Rovnice trajektorie má tvar
\[ y(x)=-\frac12g\left(\frac{x}{v_0}\right)^{\!2}+h_0=-\frac{gx^2}{2v_0^2}+h_0=Ax^2+B\;. \]Vidíme, že se jedná o kvadratickou funkci, trajektorií je tedy parabola. Na následující animaci se můžete podívat, jak je tvar trajektorie ovlivněn počátečními podmínkami.
https://www.geogebra.org/calculator/heceufbw
Vrh šikmý
Nyní se podívejme na nejobecnější pohyb v tíhovém poli. Tím je vrh šikmý. Stále se pohybujeme v tíhovém poli Země, které považujeme za homogenní. Při zavedení kartézského souřadnicového systému s osou \(x\) vodorovnou a osou \(y\) svislou bude mít zrychlení tyto složky: \(\Vec{a}=\Vec{g}=(0,-g)\). Počáteční rychlost nyní svírá s vodorovným směrem (osou \(x\)) úhel \(\alpha\), její složky tedy jsou \(\Vec{v}_0=(v_0\cos\alpha,v_0\sin\alpha)\).
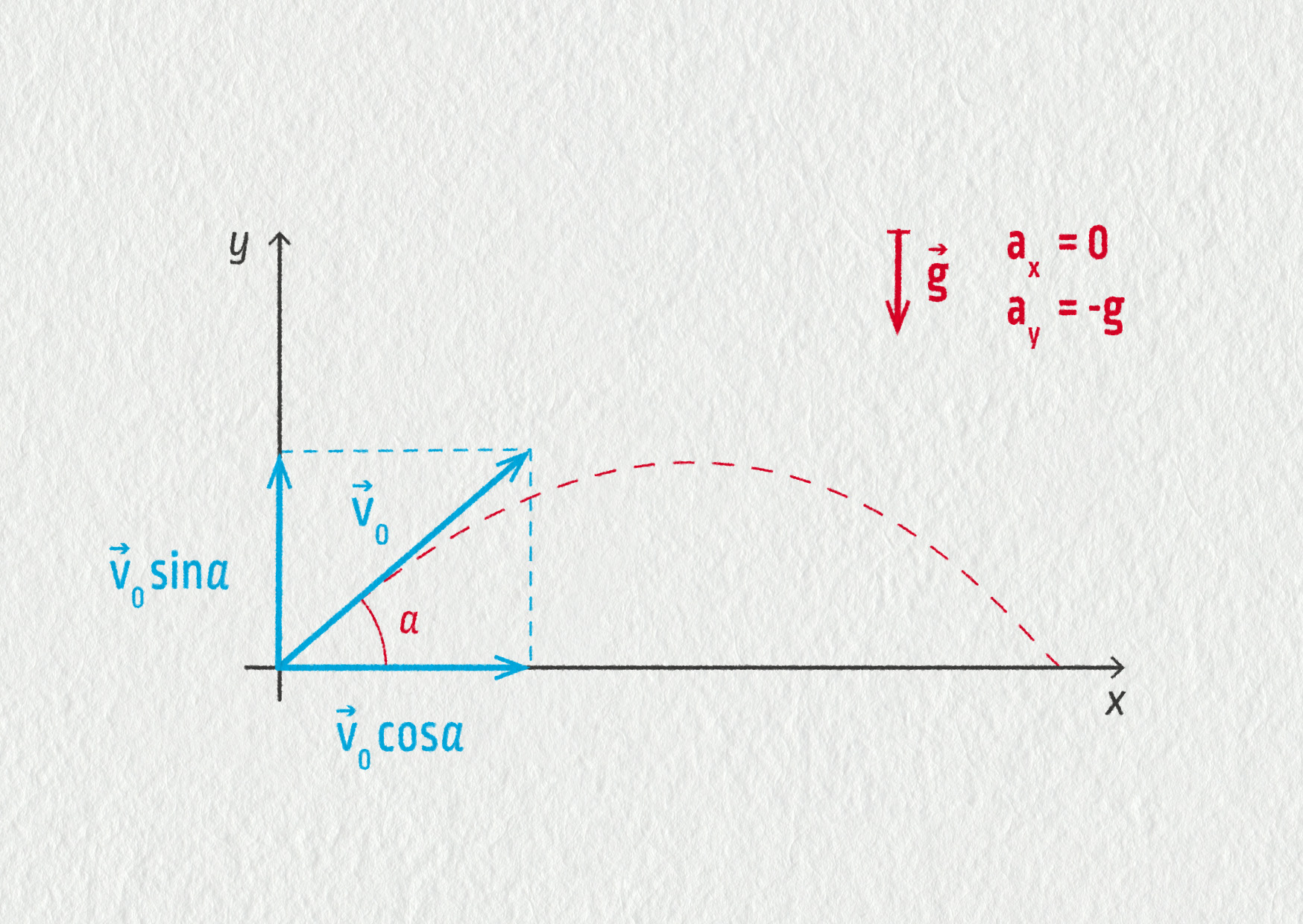
Zdroj
Opět můžeme tento pohyb rozložit na pohyb rovnoměrný ve směru osy \(x\) a rovnoměrně zpomalený/zrychlený ve směru osy \(y\). Je to dáno jedinou působící silou – tíhovou silou, která je svislá. Ve směru svislém je tedy rychlost tělesa ovlivněna zrychlením o velikosti \(-g\), což znamená nejprve rovnoměrně zpomalený pohyb ve směru svislém, poté rovnoměrně zrychlený pohyb tělesa při jeho návratu dolů. Ve směru vodorovném je zrychlení nulové, vodorovná složka rychlosti je tedy konstantní, nemění se. Pojďme si vše ukázat na konkrétním příkladu.
Jednou z možností, jak skórovat v ragby, je položení míče do brankoviště. Tým skórujícího hráče získá pět bodů. Po pětce následuje kop, tzv. konverze, za dva body. Hráč ragby má zahrát přímý kop (konverzi) ze vzdálenosti \(d=36\ \mathrm{m}\) od branky. Míč je umístěn v bodě O a hráč mu udělí počáteční rychlost svírající úhel \(\alpha=53^\circ\) vzhledem k vodorovné rovině.
- Sestavte pohybové rovnice.
- Určete rovnici trajektorie míče v soustavě souřadnic s počátkem O v místě kopu.
- Jakou minimální rychlost musí hráč udělit míči v bodě O, aby míč proletěl nad břevnem branky, které se nachází ve výšce \(h=3\ \mathrm{m}\) vzhledem k povrchu hřiště?

Zdroj

Zdroj
1) Sestavme časové rovnice pohybu. Do obecných rovnic dosadíme za zrychlení \(\Vec{a}=(0,-g)\) a za počáteční rychlost \(\Vec{v}_0=(v_0\cos\alpha,v_0\sin\alpha)\). V čase \(t=0\) se míč nachází v počátku souřadnic, proto máme \(\Vec{r}_0=(0,0)\). Souřadnice \(x\) a \(y\) míče mají tedy tvar
\[ \begin{aligned} x(t) &= v_0t\cos\alpha\\ y(t) &= -\frac12gt^2+v_0t\sin\alpha\\ \end{aligned} \]2) Abychom nalezli rovnici trajektorie a s její pomocí určili velikost minimální počáteční rychlosti pro dosažení branky, vyjádříme z první rovnice čas
\[ t=\frac{x}{v_0\cos\alpha}\; \]Ten hned dosadíme do druhé rovnice:
\[ y(x) = -\frac12g\frac{x^2}{v_0^2\cos^2\alpha}+v_0\sin\alpha\,\frac{x}{v_0\cos\alpha} = \] \[= -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\tan\alpha\cdot x=Ax^2+Bx\;. \]Opět vidíme, že trajektorií šikmého vrhu je parabola.
3) Tato parabola musí procházet bodem B (36 m, 3 m), aby byl přímý kop úspěšný a bylo dosaženo dalších dvou bodů. Případně může míč proletět brankou ve větší výšce. Za souřadnice \((x,y)\) tedy dosadíme (36 m, 3 m) a získáme rovnici s neznámou \(v_0\).
\[ 3{,}0=-\frac{9{,}81}{2v_0^2\cos^2(53^\circ)}\cdot36^2+\tan(53^\circ)\cdot36\;. \]Jejím řešením je rychlost o velikosti \(v_0=19{,}8\ \mathrm{m/s}\). Touto minimální rychlostí musí hráč pod úhlem 53° kopnout míč směrem k brance, aby bylo dosaženo dalších dvou bodů.
Celá situace je znázorněna na následující animaci. Můžete si nastavovat různé úhly a velikosti počáteční rychlosti a zkoumat, kdy již bude dosaženo branky.

Zdroj
https://www.geogebra.org/calculator/ryp6sacf
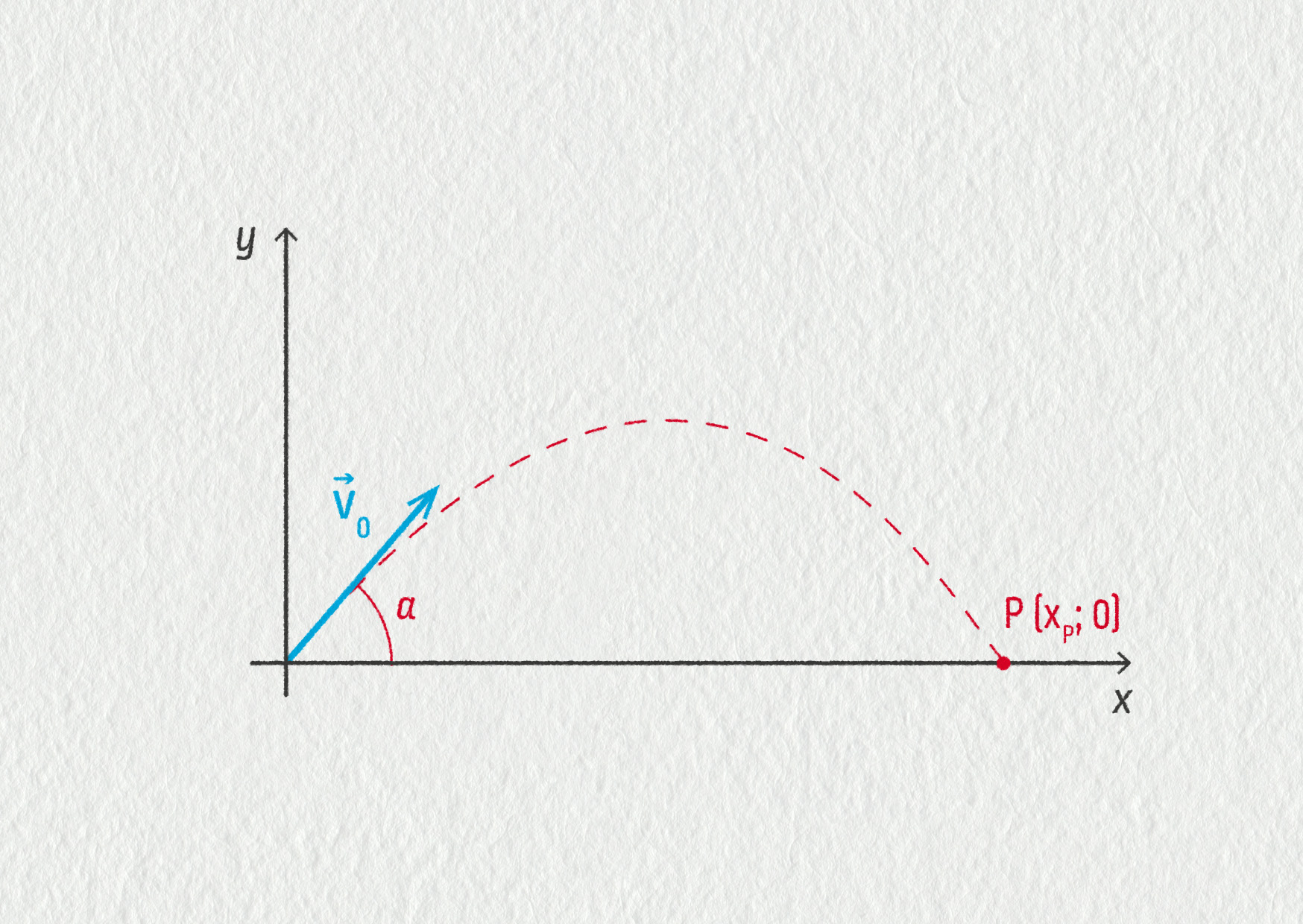
Budeme-li se ptát, co ovlivňuje délku vrhu, musíme se nejprve ptát, kam těleso dopadne. Tento bod, na následujícím obrázku označený P, má souřadnice \((x_\mathrm{P};0)\), protože místo dopadu je na zemi neboli v nulové výšce. (To v případě počátku soustavy souřadnic na povrchu země.)
Zdroj
Pro souřadnice jakéhokoliv bodu na parabolické trajektorii jsme již dříve odvodili
\[ \begin{aligned} x(t) &= v_0t\cos\alpha\\ y(t) &= -\frac12gt^2+v_0t\sin\alpha\\ \end{aligned} \]V bodě P platí, že \(y(t_\mathrm{P})=0\). Dostáváme kvadratickou rovnici pro \(t_\mathrm{P}\) bez absolutního členu.
\[ y(t_\mathrm{P})=-\frac12gt_\mathrm{P}^2+v_0t_\mathrm{P}\sin\alpha=t_\mathrm{P}\left(-\frac12gt_\mathrm{P}+v_0\sin\alpha\right)\;. \]Jejím řešením jsou hodnoty \(t_{\mathrm{P}1}=0\) a \(t_{\mathrm{P}2}=2v_0/g\cdot\sin\alpha\). První čas odpovídá počátku pohybu, kdy je těleso vrženo z počátku souřadnic, druhý čas odpovídá bodu P a okamžiku dopadu. Abychom určili, kam náš projektil dopadne, dosadíme čas dopadu \(t_{\mathrm{P}2}\) do první rovnice
\[ x_\mathrm{P}=x(t_{\mathrm{P}2})=v_0\frac{2v_0\sin\alpha}{g}\cos\alpha=\frac{v_0^2}{g}\sin2\alpha\;. \]Ve výsledném vztahu pro dostřel se tedy objevují dvě proměnné: počáteční rychlost \(v_0\) a úhel, pod kterým je těleso vrženo. Je zřejmé, že při větší počáteční rychlosti dopadne vržené těleso dále. Jak je tomu se závislostí na úhlu? Funkce sinus nabývá maximální hodnoty pro úhel roven 90°. Protože argument funkce sinus je v našem vztahu \(2\alpha\), maximální hodnoty tedy nabývá pro úhel \(\alpha=45^\circ\). Pro maximální dostřel tedy musíme těleso vyslat pod úhlem 45° vzhledem k vodorovnému směru.
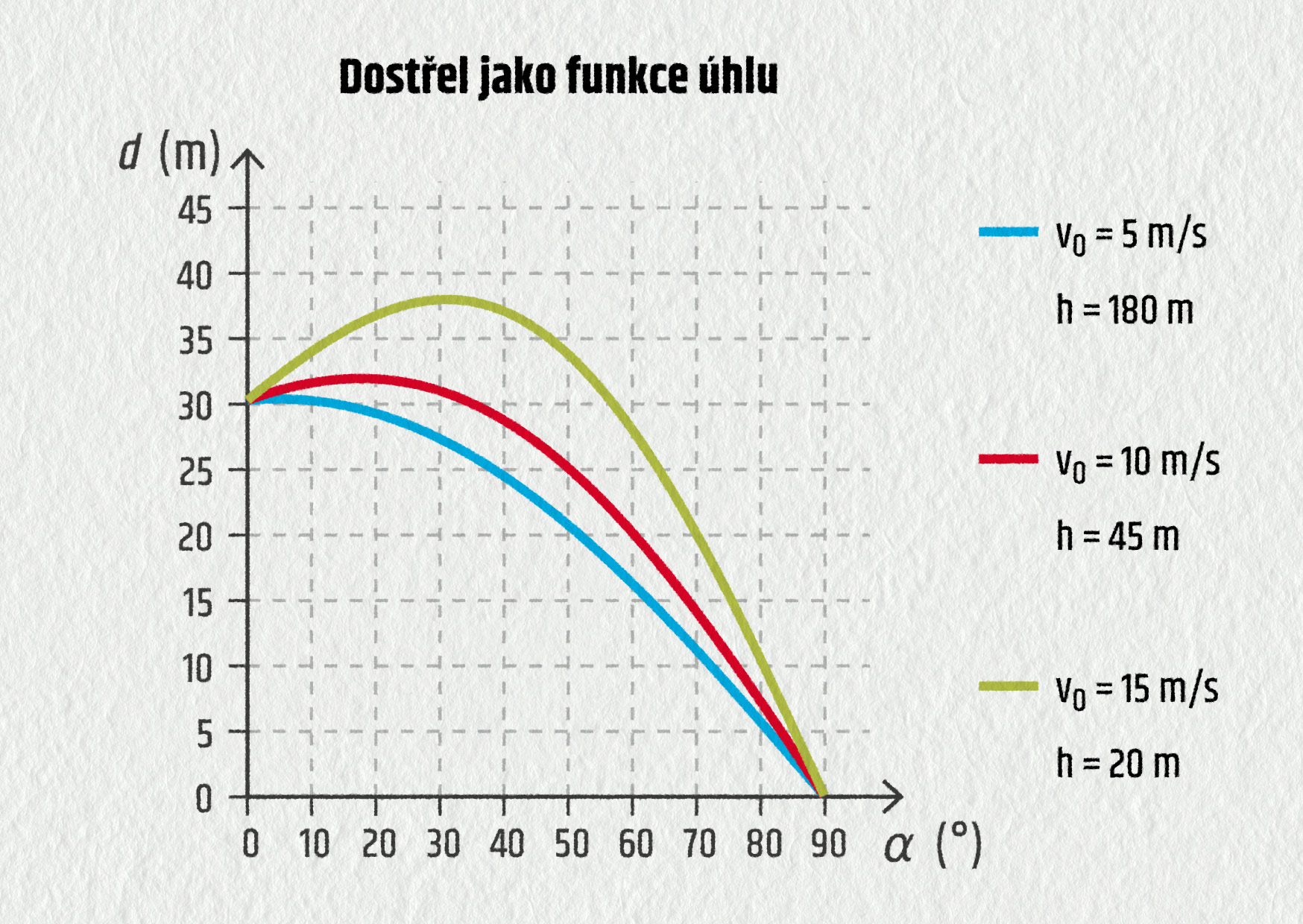
Jak se tento úhel změní, když budeme střílet z vyvýšeného místa? A jaký bude dostřel, když bychom uvažovali i tření se vzduchem? Zkuste najít alespoň některé odpovědi v následujícím grafu nebo simulaci.
Zdroj

