Dalším významným pohybem je pohyb po kružnici. Otáčivé pohyby pevných těles, jako třeba otáčení kola automobilu kolem svého středu, budeme studovat v další kapitole. V této kapitole se zaměříme na pohyby bodů a těles po kruhových trajektoriích. Jako příklad takového pohybu uveďme pohyb některých satelitů kolem Země, pohyb kolotoče nebo třeba pohyb nabité částice v kruhovém urychlovači. Jak můžeme tyto a další pohyby popsat?
Když k popisu pohybu po kružnici použijeme kartézskou soustavu souřadnic s navzájem kolmými osami, nebude to příliš výhodné. Už při rovnoměrném pohybu po kružnici se souřadnice našeho tělesa poměrně komplikovaně mění.
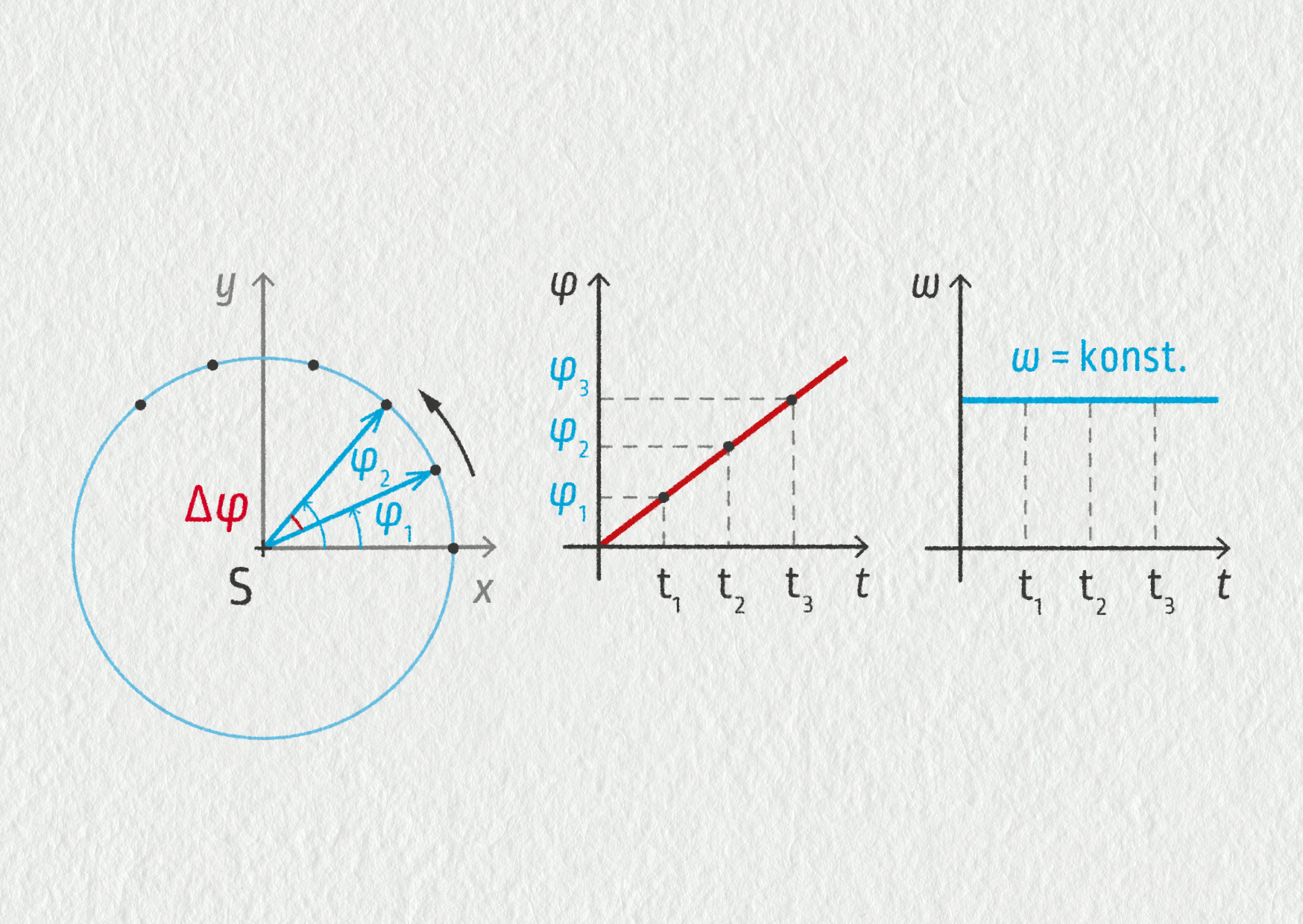
Vhodnější je pro popis pohybu použít polární souřadnice. Je-li počátek situován do středu kružnice, všechny body na trajektorii tělesa budou mít stejnou souřadnici \(r=R\) (\(R\) značí poloměr kruhové trajektorie), a tudíž k úplnému popisu pohybu tělesa bude stačit popsat změny pouze druhé souřadnice \(\varphi\). Tato souřadnice vyjadřuje úhel mezi spojnicí daného bodu se středem trajektorie a kladným směrem osy x.
Stejně jako při pohybu po přímce můžeme definovat rychlost, definujeme v polárních souřadnicích úhlovou rychlost \( \omega \).
Úhlová rychlost je podíl úhlu \(\Delta\varphi\) opsaného tělesem a doby \(\Delta t\), za kterou tato změna nastala.
Její jednotka je rad·s−1.
Vyjadřuje velikost úhlu v radiánech, který těleso opíše za 1 s.
Je-li pohyb po kružnici rovnoměrný, těleso urazí za daný čas \(\Delta t\) vždy stejný úhel \(\Delta\varphi\). Změna souřadnice \(\varphi\) je tedy lineární funkcí času a velikost úhlové rychlosti \(\omega\) je konstantní.
Zdroj
Uražená vzdálenost při rovnoměrném pohybu po kružnici odpovídá délce oblouku mezi počátečním a koncovým bodem pohybu. Můžeme ji vypočítat pomocí vztahu \(s=\overparen{AB}=R\,\Delta\varphi.\) Vezmeme-li definici průměrné rychlosti \(v_\mathrm{p}=s/\Delta t\), po dosazení získáme vztah mezi velikostí rychlosti \(v_\mathrm{p}\) a velikostí úhlové rychlosti \(\omega\):
\[ v_\mathrm{p} = \frac{s}{\Delta t} = \frac{R\,\Delta\varphi}{\Delta t}=R\omega\;. \]Čím je bod dále od středu otáčení, tím je jeho rychlost větší. Za stejnou dobu \(\Delta t\) musí urazit oblouk o větší délce.
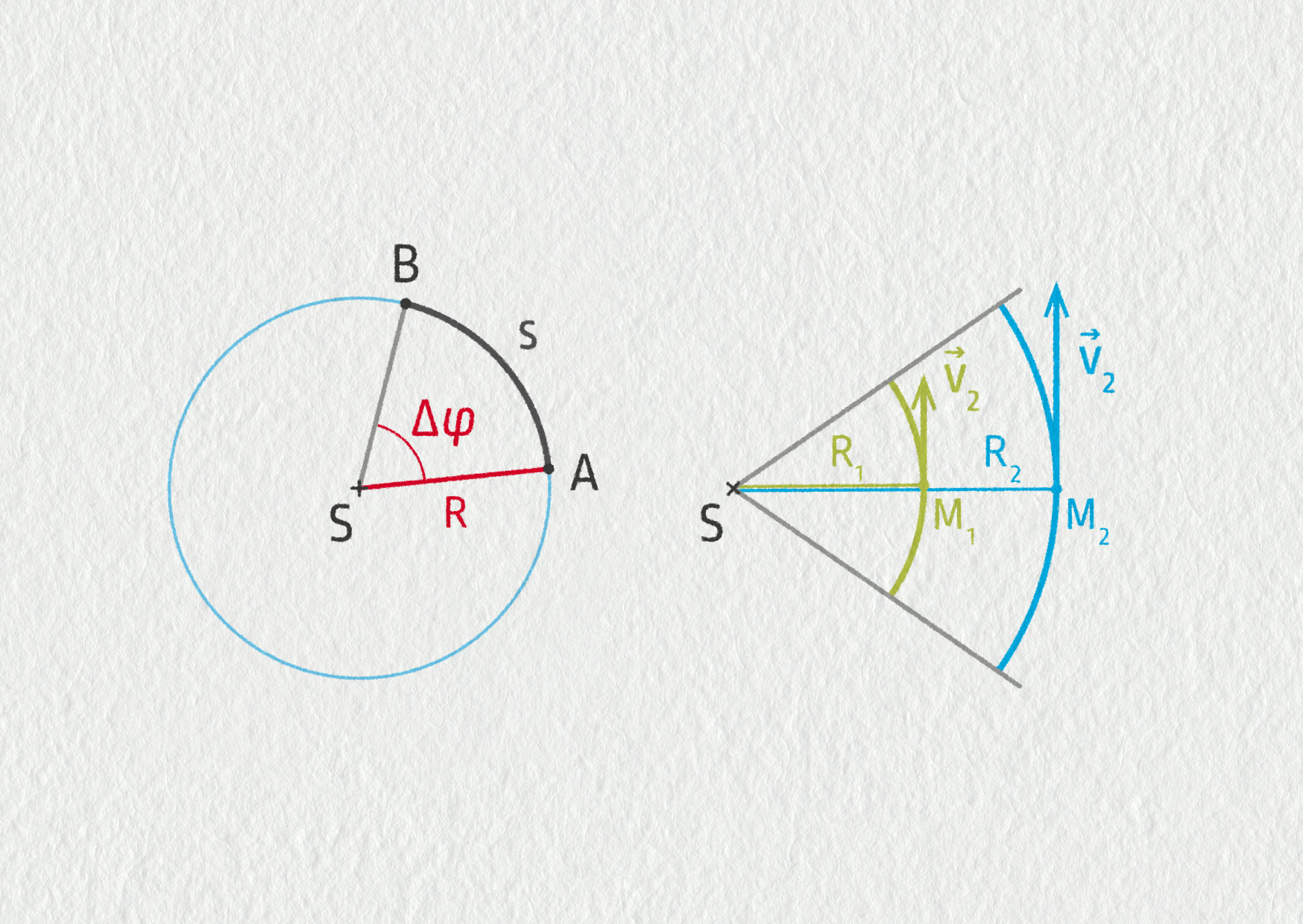
Zdroj

Zdroj
Určete velikost úhlové rychlosti tělesa, které se pohybuje po kružnici o poloměru 28 cm a opíše oblouk odpovídající úhlu 70° za 2 s. Jaká je velikost jeho rychlosti?
Nejprve spočítáme úhlovou rychlost otáčení tělesa. Vyjdeme z definice úhlové rychlosti a převedeme úhel ve stupních na radiány:
\[ \omega = \frac{\Delta\varphi}{\Delta t} = \frac{\displaystyle 70\cdot\frac{2\pi}{360}}{2}\ \mathrm{rad}\cdot\mathrm{s}^{-1}=0{,}61\ \mathrm{rad}\cdot\mathrm{s}^{-1}\;. \]Podle vztahu mezi velikostí rychlosti a úhlovou rychlostí pak píšeme \(v=\omega R=0{,}61\cdot0{,}28\ \mathrm{m}\cdot\mathrm{s}^{-1}=0{,}17\ \mathrm{m}\cdot\mathrm{s}^{-1}\).
Vzhledem k tomu, že trajektorií je uzavřená křivka, těleso se po určité době vrátí do výchozího bodu a jeho pohyb se začne opakovat. Takový pohyb nazýváme periodický. Doba, po které se pohyb začíná opakovat, je perioda \(T\). Perioda souvisí s frekvencí \(f\), která vyjadřuje počet oběhů za jednotku času.
Perioda \(T\) vyjadřuje dobu, po které se pohyb začíná opakovat. Její jednotka je sekunda.
Frekvence \(f\) vyjadřuje počet otáček za jednotku času. Její jednotka je hertz (Hz).
Vzájemně spolu souvisí vztahem \(f=1/T\).
Jestliže těleso vykoná jeden oběh po kruhové trajektorii, opíše úhel o velikosti \(2\pi\) za dobu \(T\). Úhlovou rychlost jeho pohybu tedy můžeme vyjádřit vztahem
\[ \omega=\frac{\Delta\varphi}{\Delta t}=\frac{2\pi}{T}=2\pi f\;. \]Co je příčinou, že se těleso pohybuje po kružnici?
Příčinou pohybového stavu tělesa jsou působící síly. Newtonovy pohybové zákony nám říkají, že pokud na těleso působí nenulová výsledná síla, bude zrychlení tělesa také nenulové a bude úměrné působící síle
\[ \sum_{i=1}^n \Vec{F}_i = m\Vec{a}\;. \]Těleso tak bude měnit svůj směr nebo velikost rychlosti. Nebo obojí najednou.
Zkusme nyní popsat rovnoměrný pohyb tělesa po kružnici. Jaké bude jeho zrychlení? Asi nás napadne, že při rovnoměrném pohybu tělesa je zrychlení nulové. Není tomu tak vždy, protože při křivočarém pohybu, a tedy i pohybu po kružnici, se objevuje normálové zrychlení \(\Vec{a}_\mathrm{N}\). Toto zrychlení odpovídá zakřivení trajektorie a vyjadřuje změnu směru rychlosti. Kam směřuje zrychlení při rovnoměrném pohybu po kružnici? Podívejme se na následující konstrukci zrychlení:
15.26 – Animace konstrukce vektoru zrychlení (rovnoměrný pohyb po kružnici)
https://www.geogebra.org/calculator/r7wqedmr
Zrychlení tělesa vykonávajícího rovnoměrný pohyb po kružnici směřuje vždy do středu kružnice (trajektorie). Proto bývá nazýváno dostředivým zrychlením. Jakou má toto zrychlení velikost?
Jak jsme již napsali v minulé kapitole, velikost normálového zrychlení můžeme vyjádřit vztahem \(a_\mathrm{N}=v^2/R\), kde \(v\) je velikost rychlosti tělesa a \(R\) je poloměr kruhové trajektorie.

Zdroj
Vidíme, že normálové zrychlení závisí mimo rychlosti také na poloměru trajektorie v okolí uvažovaného bodu, tudíž vyjadřuje to, že daný bod zatáčí a jak moc. Čím je poloměr trajektorie menší, tím je normálové zrychlení větší, a obráceně. Velice dobře to je vidět na následující animaci.
15.28 – Velikost normálového zrychlení závisí na poloměru trajektorie a velikosti rychlosti. V animaci můžete měnit jako poloměr trajektorie, tak velikost rychlosti tělesa.
Odkaz na Geogebru: https://www.geogebra.org/calculator/fjcvdvsb
Chcete-li se podívat, jak odvodit dříve uvedený vztah pro velikost normálového (dostředivého) zrychlení, přečtěte si následující poznámku na okraji.
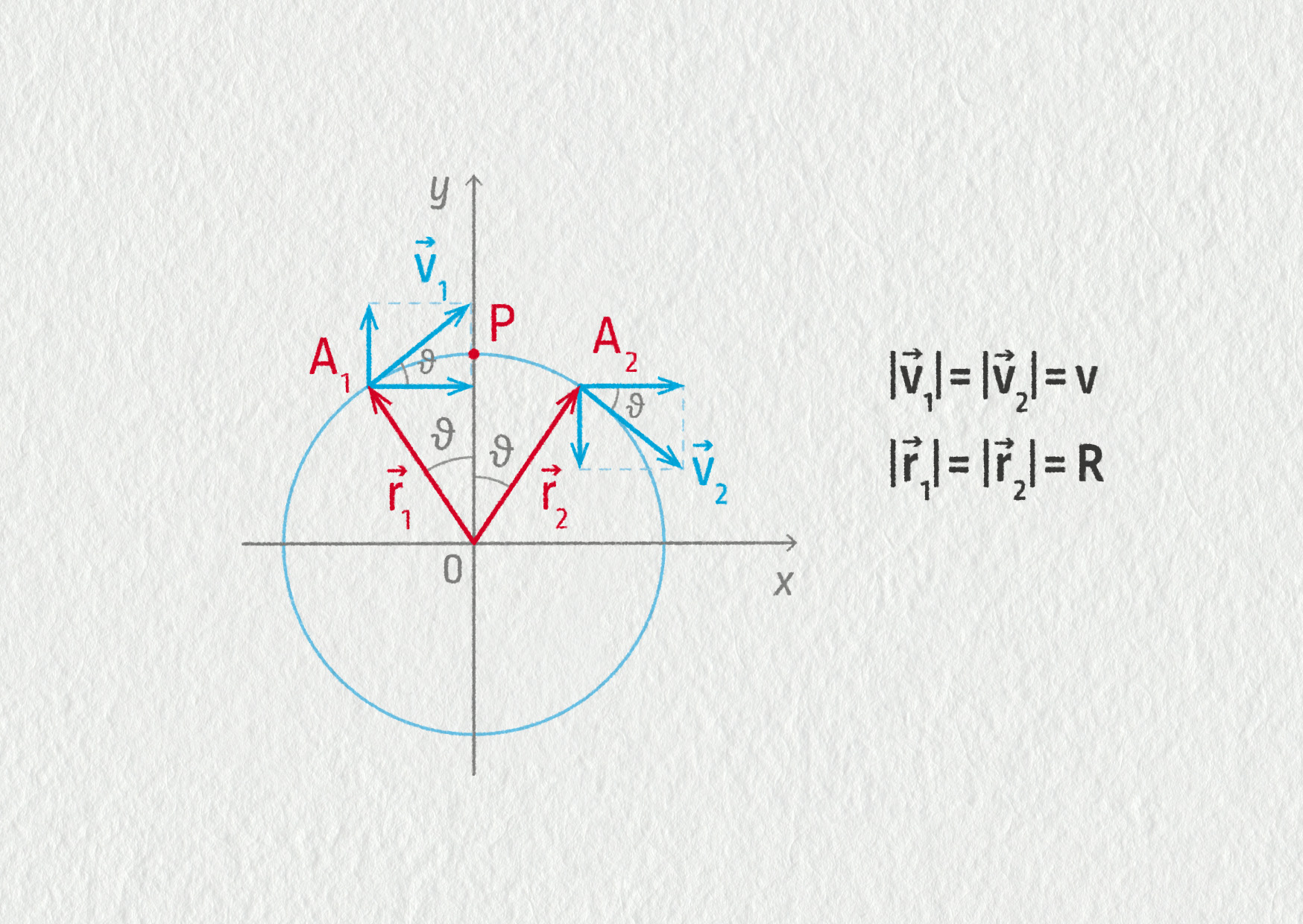
Podívejme se na těleso pohybující se rovnoměrným pohybem po kružnici. Nachází se v bodě P. Vezměme dva body A1 a A2 umístěné symetricky kolem bodu P (viz obrázek). Budou představovat dvě pozice – předcházející a následující bodu P.
Zdroj
Průměrné zrychlení můžeme vyjádřit pomocí vztahu
\[ \Vec{a}_\mathrm{p}=\frac{\Delta\Vec{v}}{\Delta t}=\frac{\Vec{v}_1-\Vec{v}_2}{\Delta t}\;. \]Rychlosti v bodech A1 a A2 můžeme vyjádřit pomocí jejich složek
\[ \begin{aligned} \Vec{v}_1 = (v_{1x},v_{1y}) &= (v\cos\vartheta,v\sin\vartheta)\\ \Vec{v}_2 = (v_{2x},v_{2y}) &= (v\cos\vartheta,-v\sin\vartheta)\\ \end{aligned} \]Pro průměrné zrychlení tedy po dosazení platí
\[ \Vec{a}_\mathrm{p}=\frac{\Delta\Vec{v}}{\Delta t}=\frac{\Vec{v}_1-\Vec{v}_2}{\Delta t}=\frac{(0,-2v\sin\vartheta)}{\Delta t}=\left(0, -\frac{2v\sin\vartheta}{\Delta t}\right)\;. \]Ze složek zrychlení v bodě P můžeme usoudit, že směr zrychlení je v záporném směru osy \(y\), což v bodě P znamená, že míří do středu trajektorie, do počátku soustavy souřadnic.
Těleso urazí dráhu odpovídající délce oblouku mezi body A1 a A2 o velikosti \(d=R\cdot2\vartheta\). Úhel \(\vartheta\) měříme v radiánech. Protože jde o pohyb rovnoměrný, tato uražená dráha je přímo úměrná času \(d=v\,\Delta t\), odkud pro čas získáme
\[ \Delta t=\frac dv=\frac{2R\vartheta}{v}\;. \]A konečně pro průměrné zrychlení pak
\[ \Vec{a}_\mathrm{p}=\left(0,-\frac{2v\sin\vartheta}{\Delta t}\right)=\left(0,-\frac{v^2}R \frac{\sin\vartheta}\vartheta \right)\;. \]Jak jsme již ukázali dříve, okamžité zrychlení je \(\Vec{a}=\lim_{\Delta t\to0}\Vec{a}_\mathrm{p}\), a proto výraz \((\sin\vartheta)/\vartheta\) jde k 1 pro \(\Delta t\to0\) (body A1 a A2 se nekonečně přibližují k bodu P) a okamžité zrychlení píšeme ve tvaru
\[ \Vec{a}=\left(0,-\frac{v^2}R\right)\;. \]Jak jsme zmínili již ve 14. kapitole, hodnota \(a_\mathrm{N}=v^2/R\) je velikost normálového zrychlení, které vyjadřuje míru zakřivení trajektorie.
Jestliže víme, kam směřuje zrychlení pohybu rovnoměrného po kružnici, víme také podle druhého Newtonova zákona, jaký je směr síly, která tento pohyb způsobuje. V některých situacích je to zřejmé, jindy musíme příčinu pohybu trochu hledat.
Pohyby po kružnici – působící síla

Zdroj

Zdroj

Zdroj
Je známo, že při sprintu na 200 m nebo 400 m dosahují běžci delších časů, než kdyby tuto vzdálenost běželi na rovném úseku. Dokážete to vysvětlit pomocí fyziky?
(Poznámka: Starty jednotlivých drah jsou proti sobě posunuty tak, aby vzdálenosti do cíle podle ideálních stop byly stejné.)
Je to způsobeno dostředivou silou, kterou běžec při běhu zatáčkou působí. To má za následek snížení síly, kterou má běžec k dispozici pro pohyb po dráze. Podle očekávání je tento efekt tím výraznější, čím menší je poloměr zatáčky. Proto si běžci často stěžují, že vnitřní dráha je „příliš úzká“.
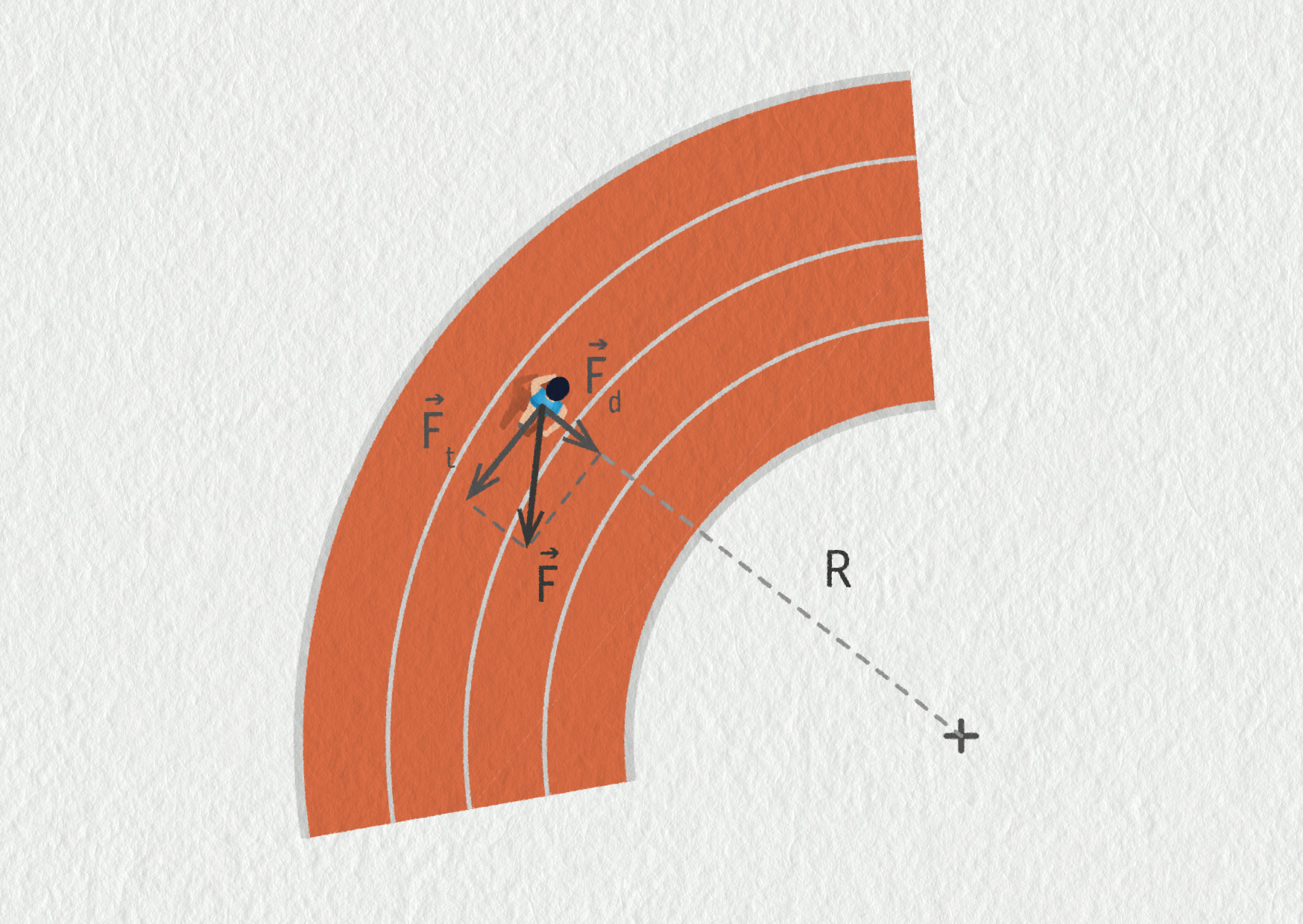
Zdroj
Obrázek ukazuje kontaktní síly působící mezi nohou běžce a zakřivenou dráhou. Poloměr zatáčky je \(R\). Běh v zatáčce nutí běžce vyvíjet dostředivou sílu \(\Vec{F}_\mathrm{d}\), aby se udržel na své zakřivené dráze. Tato dostředivá síla se přidává k síle potřebné k pohonu po dráze v tečném směru, která je značena \(\Vec{F}_\mathrm{t}\). Celková síla \(\Vec{F}\) (působící dráhou na běžce) má složky \(\Vec{F}_\mathrm{t}\) a \(\Vec{F}_\mathrm{d}\).
Pokud by běžec v dráze č. 1 (nejvnitřnější dráha) uběhl 200 m za 19,72 s, v dráze 8 (nejvzdálenější dráha) by ji uběhl za 19,60 s. To je docela velký časový rozdíl, který se v cíli promítá do vzdálenosti přibližně 1 metr. Zvláště když si uvědomíme, že mnoho závodů se vyhrává nebo prohrává o pouhé centimetry…
Je však třeba zdůraznit, že ani sprinteři nepovažují dráhu č. 8 za nejvýhodnější, protože vzhledem k rozloženým startům by běželi polovinu závodu před ostatními běžci, což je staví do psychické nevýhody, že nevidí, co dělají ostatní běžci.

