Výkon
Fyzikální veličina práce závisí jen na síle a posunutí. Něco se někam posunulo a odvedla se nějaká práce. V běžném životě také měříme množství práce (vykopání brambor, posečení louky apod.), zajímavé však je také, za jak dlouho byla daná práce vykonána. Když posečete stejnou louku do oběda, váš výkon bude jistě vyšší, než když na ní budete pracovat ještě v půli odpoledne.
Ve fyzice je tomu stejně. Rychlost konání práce popisuje veličina zvaná výkon. Definujeme ho jako podíl práce W a odpovídajícího času t.
Jeho jednotkou je J/s = W (watt).
Tabulka výkonů (maximální výkony):
| zdroj | přibližný výkon (W) |
|---|---|
| raketa Saturn | 88 000 000 000 |
| soustava elektráren Tři soutěsky (Čína) – instalovaný výkon | 22 500 000 000 |
| jaderná elektrárna Temelín | 2 168 000 000 |
| Queen Mary II | 115 000 000 |
| Pendolino | 4 000 000 |
| sportovní vůz Dodge Viper | 365 000 |
| nákladní automobil Tatra 815 | 250 000 |
| osobní automobil Škoda Karoq 1.5 TSI | 110 000 |
| skútr Kentoya Fever 125 cm3 | 5 000 |
| vrcholový cyklista při sprintu | 1 400 |
| vrcholový sportovec dlouhodobě (maraton) | 300 |
| člověk jdoucí do schodů | 150 |
| člověk při chůzi | 60 |
Další zajímavé hodnoty výkonů naleznete na: http://www.komplexnizdravi.cz/pohyb/energeticky-vydej-cloveka-pri-sportu-a-praci/
U automobilů se často setkáme také se starší jednotkou výkonu koňskou silou (horse power):
1 hp (koňská síla) = 746 W
O historii této jednotky, odvozené od výkonu koně, se dočtete v následující poznámce.
Poznámka na okraj: Koňská síla
Dříve používaná jednotka výkonu koňská síla byla zavedena Jamesem Wattem. Vznikla z potřeby porovnat výkon nově vzniklého parního stroje s něčím, co existovalo předtím. A z hlediska výkonu to byli právě koně. Měl-li si investor do parního stroje představit, jak výkonný bude jeho nový pohon, mohl to porovnat právě s doposud používanými koňmi. Jedna koňská síla odpovídá podle Watta výkonu koně, který dlouhodobě chodí v žentouru rychlostí 1 m/s a zvedá přitom náklad o hmotnosti cca 80 kg. Můžete si sami ověřit, zda tato definice odpovídá uvedenému vztahu.
Zdroj
Nakonec několik hodnot výkonů automobilových motorů:
| automobil | výkon (kW) | výkon (hp) |
|---|---|---|
| Trabant 601 | 19 | 26 |
| Škoda Octavia 1,6 TDI | 85 | 115 |
| Bugatti Veyron | 882 | 1200 |
| Tesla model S P100D | 568 | 762 |
Příklad 1
Výsledek: 429 W; při normální chůzi do schodů máme výkon asi 150 W, špičkově dokáže člověk vyvinout až výkon kolem 1 500 W – například atlet při startu běhu na 100 m nebo při sprintu v cyklistice.
Uvažujeme-li nyní automobil jedoucí konstantní rychlostí, musí motor automobilu vyvinout sílu, která vyrovná účinek tření a odporu vzduchu. Jestliže automobil urazí vzdálenost s, motor vykoná práci W a pro jeho výkon platí:
\[P=\frac{W}{t}=\frac{Fs}{t}=Fv\;,\]protože vzdálenost uražená za čas odpovídá velikosti jeho rychlosti \(v=s/t\).
Poznámka na okraj: Okamžitý výkon
Pokud je rychlost tělesa v každém okamžiku jiná, výkon je nazýván okamžitý a jeho velikost vypočítáme podle vztahu:
\[P=\frac{\mathrm{d}W}{\mathrm{d}t}=Fv\]Říkáme, že okamžitý výkon je derivací práce podle času.
Příklad 2
\(P=Fv\), odtud \(v=P/F=42\,000/1500\ \mathrm{m/s}=28\ \mathrm{m/s}=101\ \mathrm{km/h}\).
Všimněte si, že síla motoru je větší než průmět tíhové síly do nakloněné roviny \(mg\sin\alpha\). Motor musí překonávat také odporové síly.
Účinnost
S výkonem úzce souvisí i veličina příkon. Jestliže výkon je množství práce nebo energie vykonané za čas, příkon je roven množství práce nebo energie spotřebované za stejný čas.
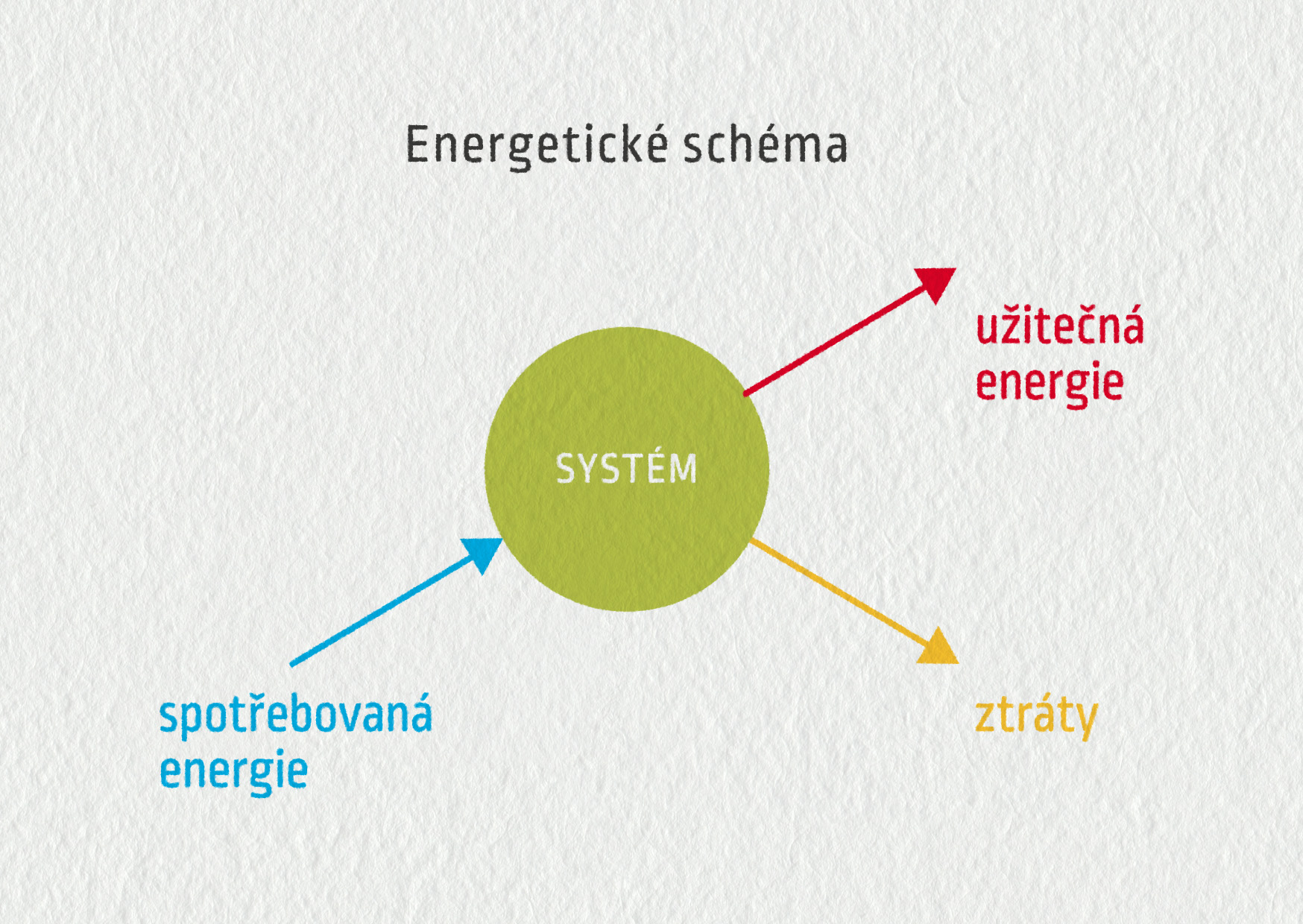
Zdroj
V tomto schématu vidíme, že když nějaký systém přijímá energii a přeměňuje ji na jiné formy energie, celkové množství energie zůstává konstantní. Sledujeme-li, jaké množství energie bylo změněno na jinou formu, zavádíme veličinu účinnost \(\eta\) (éta). Je definována podílem:
\[\eta=\frac{\hbox{energie užitečná}}{\hbox{energie spotřebovaná}}=\frac{\hbox{výkon}}{\hbox{příkon}}\]Účinnost je bezrozměrná veličina (podíl dvou energií nebo výkonů), vyjadřujeme ji číslem mezi 0 a 1, neboť užitečná energie je menší než spotřebovaná energie, a to o ztráty. Na následující galerii si můžete prohlédnout energetické schéma žárovky, vysavače a spalovacího motoru.
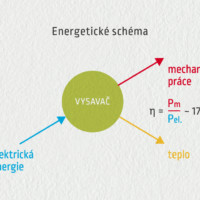
Zdroj
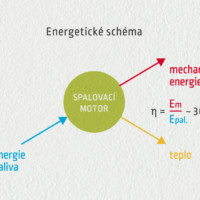
Zdroj
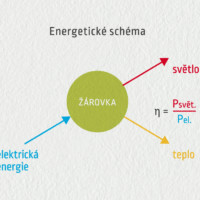
Zdroj
Příklad 3
\[\eta=\frac{\hbox{sací výkon}}{\hbox{příkon}}\]
odtud pak dostáváme pro první vysavač:
\[\hbox{sací výkon}=\eta\cdot\hbox{příkon}=0{,}22\cdot750\ \mathrm{W}=162\ \mathrm{W}\]a pro druhý vysavač:
\[\hbox{sací výkon}=\eta\cdot\hbox{příkon}=0{,}27\cdot700\ \mathrm{W}=186\ \mathrm{W}\]Větší výkon má druhý vysavač.
