Zákon síly
Cvičení 1
Běžné SUV má hmotnost 1 500 kg a z klidu na rychlost 100 km/h se rozjede za 10 s. Vypočítejte tahovou sílu motoru.
Cvičení 2
S využitím 2. Newtonova zákona odvoďte, že pokud je zanedbatelný odpor vzduchu, všechna tělesa padají se stejným zrychlením a = g.
Cvičení 3
Na startu lyžařského závodu má svah sklon a = 12°. Vypočítejte, s jakým zrychlením se bude pohybovat lyžařka Lucka. Předpokládejte, že má dobře namazané lyže (zanedbatelné tření) a že má aerodynamickou postavu (zanedbatelný odpor vzduchu). Hmotnost označíme m – nepodařilo se ji zjistit.
Vypočítejte, za jak dlouho a na jaké dráze dosáhne rychlosti 90 km/h.
Cvičení 4
Určete, jak velkou gravitační silou přitahuje Slunce Zemi. K výpočtu stačí znát jen hmotnost Země (6 ∙ 1024 kg), střední vzdálenost od Slunce (150 milionů km) a dobu oběhu všichni znáte.
Cvičení 5
Táhnete svou mladší sestru na sáňkách silou 120 N, když tu náhle najedete na zledovatělý povrch (uvažujme pohyb bez tření). Saně se začnou pohybovat se zrychlením 2,5 m/s2. Určete hmotnost sestry, jestliže samotné saně mají hmotnost 7,5 kg.
Cvičení 6
Kulečníkové kouli o hmotnosti 0,170 kg je během 4,0 ms udělena rychlost 12 m/s. Vypočítejte sílu, která na kouli působila během této doby a uvedla ji do pohybu.
Cvičení 7
Představme si experiment, ve kterém upustíme ze stejné výšky dvě stejně velké koule. První kovová má větší hmotnost než druhá dřevěná.
- Je doba pádu první koule větší, stejná nebo menší než doba pádu druhé koule?
- Vyberte nejsprávnější vysvětlení z následujících:
- Tíhové zrychlení je stejné pro všechny předměty bez ohledu na jejich hmotnost.
- Hmotnější kouli je těžší urychlit.
- Odpor vzduchu má menší účinek na těžší kouli.
Cvičení 8
Chytač v baseballu zachytí míček letící rychlostí 144 km/h do své rukavice a zastaví jej na dráze 0,15 m. Předpokládáme-li, že na míček působí silou o velikosti 800 N, určete hmotnost míčku.

Zdroj
Cvičení 9
Automobil jede rychlostí 16,0 m/s, když v tom řidič uvidí na cestě skákající míč. Začne brzdit a během 1,20 s se jeho rychlost sníží na 9,5 m/s. Hmotnost automobilu je 950 kg.
- Určete průměrnou brzdnou sílu automobilu.
- Určete dráhu, kterou automobil ujel při tomto zpomalení.
- 5,1 kN
- 15,5 m
Cvičení 10
Přistávající letadlo Jetliner A747 má hmotnost 3,50 ⋅ 105 kg. Má rychlost 27,0 m/s a působí na něj brzdící síla 4,30 ⋅ 105 N.
- Jaká bude jeho rychlost po 7,50 s brzdění?
- Jakou dráhu letadlo urazí během této doby?
- 17,8 m/s
- 168 m
Cvičení 11
Při odkopu od branky působí noha brankáře na míč průměrnou silou F = 297 N. S jakým zrychlením se míč pohybuje, je-li jeho hmotnost 450 g? Jakou rychlost míč získá, působí-li noha po dobu 0,05 s? Zanedbejte vliv ostatních sil.
Cvičení 12
Člověk je schopen při roztlačování auta vyvinout sílu 250 N. Valivý odpor plus tření v ložiskách, které působí proti pohybu auta, činí dohromady 150 N. Hmotnost auta je 1500 kg. S jakým zrychlením je možné auto roztlačit? Za jak dlouho dosáhne auto rychlosti 6 km/h?
Cvičení 13
Auto s největším zrychlením na světě je Porsche 918 Spyder. Při hmotnosti 1,7 t zrychlí z 0 na 100 km/h za pouhých 2,2 s. Vypočítejte průměrnou tahovou sílu motoru. Údaj se vztahuje k přímočarému pohybu po vodorovné silnici, zanedbáváme odpor vzduchu.
Cvičení 14
Tatrovka jede po vodorovné silnici rychlostí v0 = 64,8 km/h. V určitém okamžiku vstoupí do vozovky nepozorný chodec a řidič začne prudce brzdit. Maximální síla, kterou brzdy vyvinou, je 66 kN. Vypočítejte velikost zrychlení a brzdnou dráhu. Hmotnost plně naložené Tatrovky je 22 t.
Cvičení 15
K čemu slouží ABS čili Anti-lock Brake System? Při prudkém brzdění se kola u starých aut, která nemají ABS, zastaví a kloužou po asfaltu smykem se součinitelem dynamického tření fd = 0,55. Pokud je antiblokovací systém ABS aktivní, kola neprokluzují a je možné využít maximální hodnoty součinitele statického tření fs = 0,60. Spočítejte pro oba případy zrychlení a brzdnou dráhu při vodorovném pohybu s počáteční rychlostí v0 = 90 km/h.

Zdroj
Cvičení 16
Tento odstrašující příklad má ukázat, k čemu jsou dobré autosedačky pro děti. Místo toho, aby usadila dítě o hmotnosti 9 kg do sedačky, drží je maminka na klíně. Při nehodě narazí auto v rychlosti 45 km/h do překážky a zastaví se za 0,1 s. Jakou silou by musela maminka dítě držet, aby se pohyb dítěte zastavil spolu s autem a s ní? Co se stane ve skutečnosti?
Cvičení 17
Dospělý člověk o hmotnosti 80 kg stojí ve výtahu. Vypočítejte, jak velkou silou bude působit nohama na podlahu výtahu, jestliže:
- je výtah v klidu,
- se výtah rozjíždí dolů se zrychlením 2 m/s2,
- jede výtah rovnoměrným pohybem nahoru rychlostí 2,5 m/s,
- se výtah rozjíždí nahoru tak, že na dráze 4 m získá rychlost 2 m/s.
- 800 N
- 640 N
- 800 N
- 840 N
Cvičení 18
Na základě analýzy grafu zrychlení výtahu v závislosti na čase, určete, jak se kabina výtahu pohybovala. v čase t = 0 s byl výtah v klidu.
- Popište jednotlivé fáze jejího pohybu.
- Rozjela se nejprve nahoru nebo dolů?
- Jaké rychlosti dosáhla, jestliže zrychlení kabiny vždy trvalo právě 2,0 s?
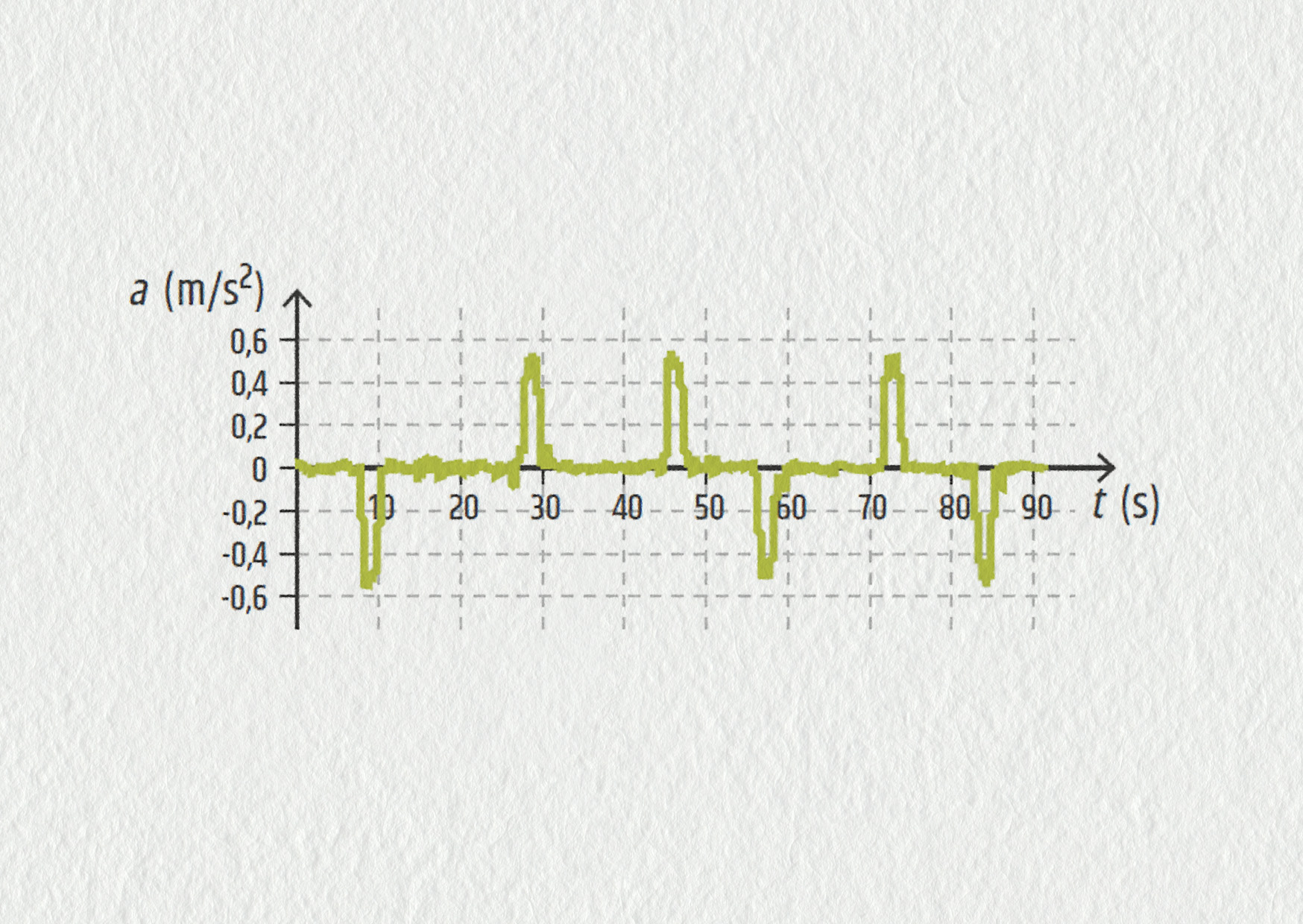
Zdroj
- a) klid (0–8 s) – rovnoměrně zrychlený pohyb dolů (8–10 s) – rovnoměrný pohyb dolů (10–28 s) – rovnoměrně zpomalený pohyb (28–30 s) – klid (30–46 s) – rovnoměrně zrychlený pohyb vzhůru (46–48 s), rovnoměrný pohyb vzhůru (48–57 s), …
- dolů, zrychlení je záporné
- 1,0 m/s
Cvičení 19
Auto o hmotnosti 1 200 kg projíždí kruhovým objezdem o poloměru 25 m rychlostí 30,6 km/h. Která síla způsobuje, že auto zatáčí? Vypočítejte její velikost.
Cvičení 20
Určete, jak velkou gravitační silou přitahuje Země Měsíc. Hmotnost Měsíce je 7,35 ∙ 1022 kg, jeho střední vzdálenost od Země 384 000 km a perioda oběhu po kružnici 27,3 dne.
Cvičení 21
Malá kovová kulička o hmotnosti 200 g je zavěšena na tenké niti o délce 80 cm. Vypočítejte tahovou sílu niti, pokud:
- kulička visí v klidu v nejnižší poloze,
- kulička je rozhoupaná a prochází rychlostí 2 m/s rovnovážnou polohou.
- 2 N
- 3 N
Cvičení 22
Vypočítejte, s jakým zrychlením se bude rozjíždět auto o hmotnosti 1,2 t do kopce o sklonu 6,8°, je-li tahová síla motoru 2,2 kN a odporová síla 0,3 kN.
Cvičení 23
Lyžařka Katka sjíždí svah, který má sklon 13,5°. Součinitel smykového tření mezi lyžemi a sněhem je 0,08. Za jak dlouho získá rychlost 100 km/h, rozjíždí-li se z klidu? Katka má aerodynamickou postavu a jezdí zásadně šusem.
Cvičení 24
Předpokládejme kulovou kapičku vodní mlhy o hmotnosti m a hustotě \(\varrho=1{,}0\ \mathrm{g/cm}^3\), mající poloměr r. Kapka padá svisle dolů, působí na ni odporová síla úměrná rychlosti (\(F_\mathrm{O}=6\pi\eta rv\)) a těsně před dopadem na zem dosáhne kapka své mezní rychlosti o velikosti 1,5 cm/s. Při řešení úlohy uvažujte dynamickou viskozitu vzduchu η = 1,3 ∙ 10-3 Pa ∙ s-1 při 10 °C. Určete poloměr vodní kapičky r.
Cvičení 25
Řetízkový kolotoč vykoná jednu otáčku za 5 s. Poloměr kružnice, po níž se pohybuje sedačka kolotoče, je 4,0 m. Jaký úhel svírá závěs sedačky se svislým směrem?
Cvičení 26
Motorkář projíždí neklopenou vodorovnou zatáčkou o poloměru 100 m. Zatáčí díky třecí síle mezi koly a silnicí. Jakou maximální rychlostí může jet, aniž by dostal smyk? Součinitel smykového tření mezi pneumatikou a mokrým asfaltem je 0,30.

Zdroj
Cvičení 27
Těleso o hmotnosti m1 = 0,5 kg leží na vodorovném stole a je uváděno do pohybu visícím závažím o hmotnosti m2 = 0,3 kg, které je k němu připevněno nití vedenou přes kladku. Součinitel smykového tření mezi tělesem a povrchem stolu je 0,20. Určete velikost zrychlení tělesa a sílu, kterou je napínána nit.

