Podívejme se nyní detailně na nejjednodušší a nejrozšířenější prvek ve vesmíru. Na příkladu vodíku si ukážeme, jak uplatnit pravidla vysvětlená v předchozím textu.
Jestliže na výbojku s vodíkem přivedeme napětí 5 000 V, molekuly plynného H2 jsou pomocí elektrického výboje disociovány na atomy vodíku H. Po jejich excitaci při následném návratu do základního stavu budou tyto atomy vytvářet fotony charakteristických vlnových délek a výbojka bude vydávat jasné růžové světlo. Podíváme-li se na ni spektroskopem nebo spektrometrem, zjistíme, jak vypadá spektrum vodíku.
Vodíková výbojka a spektrum vodíku

Zdroj
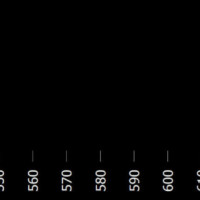
Zdroj
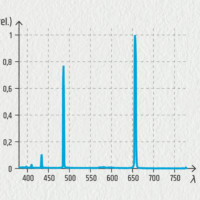
Zdroj
V emisním spektru vodíku najdeme 4 barevné čáry ve viditelné oblasti. Jejich vlnové délky a značení jsou Hα 656,3 nm (červená), Hβ 486,1 nm (světle modrá), Hγ 434,0 nm (indigová) a Hδ 410,2 nm (fialová). Poslední z nich je velice slabá a špatně viditelná. Podle objevitele matematického výrazu poskytujícího tyto vlnové délky je nazýváme Balmerovou sérií.
Existují však i spektrální čáry okem neviditelné, například v ultrafialové oblasti nebo v infračervené oblasti. V tomto případě hovoříme o Lymanově sérii nebo o sérii Paschenově, Brackettově či Pfundově.
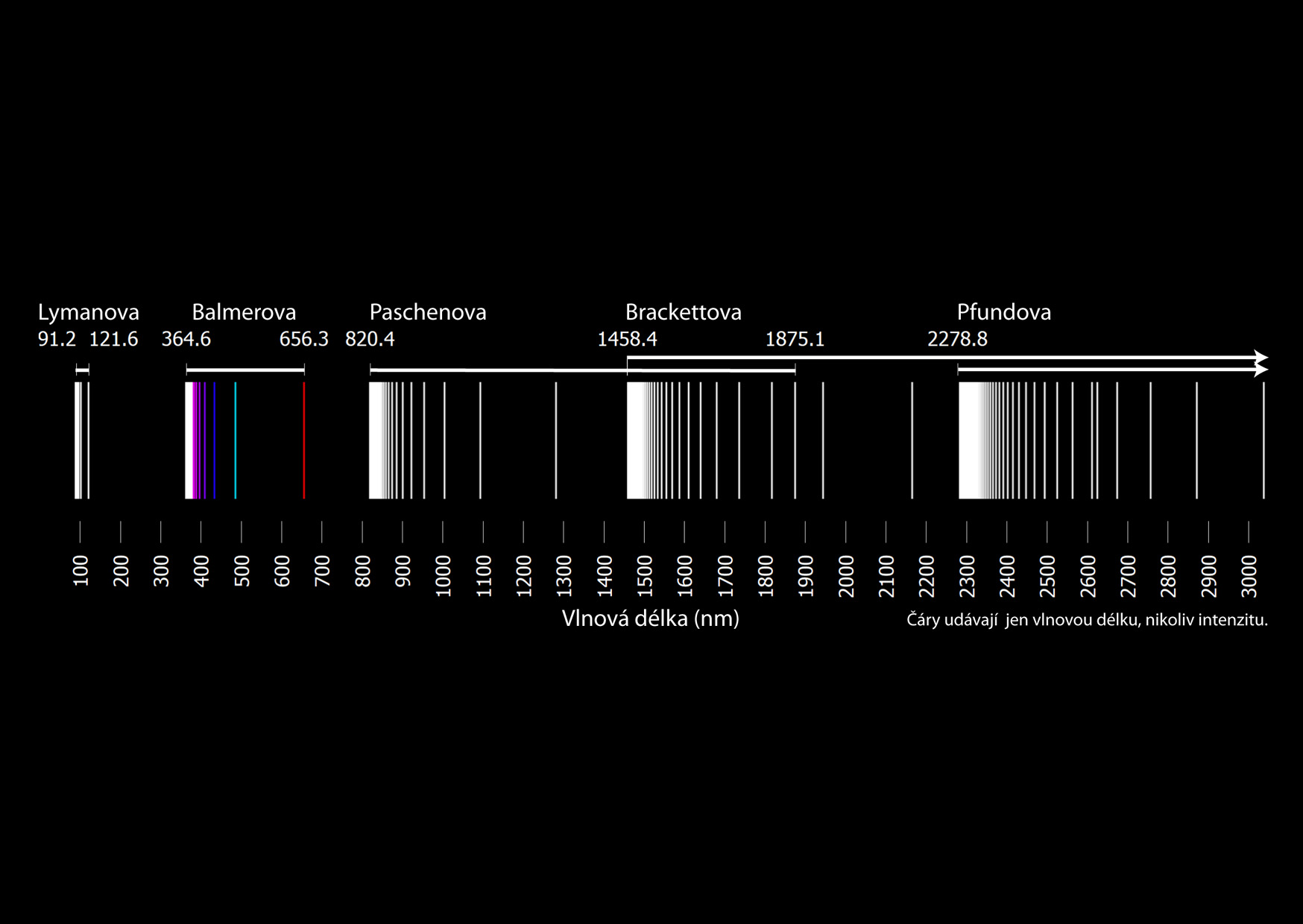
Zdroj
Pozorovaná spektra jsme ale dlouho neuměli vysvětlit.
Johann Balmer a Johann Rydberg dokonce sestavili matematický vztah, který umožňoval vypočítat vlnové délky emitovaných spektrálních čar:
\[ \frac1{\lambda_{nm}} = R_\mathrm{H}\left(\frac1{m^2}-\frac1{n^2}\right)\;. \]Byl to čistě empirický vztah a nikdo jej neuměl vysvětlit na základě žádné teorie.
Řešení přinesl v roce 1913 právě Niels Bohr svým kvantováním energie v atomu a modelem atomu vodíku. Zde uvádíme základní Bohrovy postuláty, na kterých je postaven jeho model atomu:
- V atomu existují stacionární stavy, na kterých se elektron pohybuje podle zákonů klasické mechaniky. Na těchto hladinách elektron nevyzařuje energii, a je tedy stabilní.
- Ke změně energie dochází pouze při přeskoku elektronu z jedné hladiny na druhou. Pokud energii elektronu dodáme, přeskočí na vyšší hladinu, a naopak. Tato energie je rovna \(E=hf\), což znamená, že se při přeskoku buď absorbuje, nebo vyzáří foton s frekvencí \(f\) (\(h\) zde značí Planckovu konstantu).
- Dráhy, na kterých se elektron může pohybovat, musí splňovat \(L=n\,h/2\pi\), tedy že úhlový moment hybnosti elektronu musí být celočíselným násobkem redukované Planckovy konstanty.
Podle Bohra se elektrony v atomu vodíku pohybují kolem jádra po kružnicích v určitých hladinách a jejich energie je stálá. Třetí postulát pak hovoří o kvantování momentu hybnosti, což je veličina popisující rotační pohyb tělesa, v našem případě elektronu kolem jádra.
Myšlenka to byla převratná, protože Planckovu teorii kvantování již dříve (1905) Einstein použil na světlo a nyní (1913) ji Bohr uplatnil i na jiné objekty než světlo. Bohrův model byl velmi rychle přijat, neboť umožnil jednoduše vysvětlit pozorované jevy. Za svůj přínos k popisu atomu byl Niels Bohr v roce 1922 odměněn Nobelovou cenou.
Abychom pochopili, jak vzniká spektrum vodíku, musíme v souladu s Bohrem nejprve předpokládat, že hodnoty energií v základním nebo v excitovaném stavu závisí na hodnotě hlavního kvantového čísla \(n\). Značíme je \(E_n\) a můžeme je vyjádřit jednoduchým matematickým vztahem:
Jestliže se elektron nachází na hladině \(n\), energii atomu vodíku H je možné vyjádřit vztahem
\[ E_n = -\frac{E_0}{n^2}\;. \]\(E_0 = 13{,}6\ \mathrm{eV}\) – ionizační energie atomu vodíku,
\(n\) – hodnota hlavního kvantového čísla.
Hodnoty energií jsou záporné, protože nulovou hladinu (\(E=0\ \mathrm{eV}\)) jsme zvolili v takovém stavu, kdy elektron již není vázán v atomu. Jde tedy o ionizovaný stav atomu vodíku H+.
Dnes atom vodíku popisujeme pomocí kvantové fyziky. Z ní již vyplývá, že energie příslušející jednotlivým stavům atomu vodíku závisí na hlavním kvantovém čísle. V Bohrově době, tj. na počátku 20. století, však myšlenka kvantování energií byla zcela nová a značně revoluční.
Výpočet energetických hladin vodíku
Na základě vztahu pro energii elektronu vypočítejte energie prvních pěti hladin (\(n=1,2,3,4,5\)). Poté je znázorněte do energetického diagramu a přidejte hladinu odpovídající volnému elektronu (\(n\to\infty\)).
Základní stav odpovídá hlavnímu kvantovému číslu \(n=1\). Je to základní stav atomu vodíku a jeho energie má hodnotu
\[ n=1 \quad\Rightarrow\quad E=E_1=-\frac{E_0}{1^2} = -13{,}6\ \mathrm{eV} \]Pro první excitovaný stav (\(n=2\)) dostáváme
\[ n=2 \quad\Rightarrow\quad E=E_2=-\frac{E_0}{2^2} = -3{,}40\ \mathrm{eV} \]Pro druhý excitovaný stav (\(n=3\)) pak platí:
\[ n=3 \quad\Rightarrow\quad E=E_3=-\frac{E_0}{3^2} = -1{,}51\ \mathrm{eV} \]Čím výše jsou vrstvy, ve kterých se nacházejí elektrony, tím těsněji u sebe jsou jejich energetické hladiny. Jejich energie jsou poměrně blízké, což vidíme na celkovém energetickém diagramu atomu vodíku (viz energetické schéma atomu vodíku na obrázku 25.29).
Výpočet vlnové délky spektrálních čar vodíku
Vypočítejte vlnovou délku fotonu, který vznikl přeskokem elektronu mezi
- prvním excitovaným a základním stavem;
- druhým a prvním excitovaným stavem;
- třetím a prvním excitovaným stavem;
- čtvrtým a druhým excitovaným stavem.
Abychom určili velikost vlnové délky fotonu vyzářeného při přeskoku mezi hladinami s hlavními kvantovými čísly \(n\) a \(m\), přičemž \(n>m\), vyjádříme nejprve hodnoty energií příslušejících těmto stavům. Pro počáteční stav \(n\) platí:
\[ E_n = -\frac{E_0}{n^2}\;. \]Pro koncový stav \(m\) píšeme analogicky
\[ E_m = -\frac{E_0}{m^2}\;. \]Rozdíl energií lze tedy vyjádřit pomocí vztahu
\[ \Delta E = E_n - E_m = -\frac{E_0}{n^2} - \left(\frac{E_0}{m^2}\right) = E_0\left(\frac1{m^2}-\frac1{n^2}\right) = \frac{hc}{\lambda_{nm}}\;. \]Odtud pak můžeme vyjádřit požadovanou vlnovou délku odpovídající určitému přeskoku mezi dvěma hladinami vztahem
\[ \frac1{\lambda_{nm}} = \frac{E_0}{hc}\left(\frac1{m^2}-\frac1{n^2}\right) = R_\mathrm{H}\left(\frac1{m^2}-\frac1{n^2}\right)\;, \]kde jsme pro zjednodušení zavedli Rydbergovu konstantu pomocí
\[ R_\mathrm{H} = \frac{E_0}{hc} \approx 1{,}097\cdot10^{7}\ \mathrm{m}^{-1}\;. \]Vlnová délka fotonu, který vznikne přeskokem mezi prvním excitovaným stavem (\(n=2\)) a základním stavem (\(m=1\)), je \(\lambda_{21}=121{,}6\ \mathrm{nm}\). Tato vlnová délka odpovídá ultrafialovému záření a je základní čarou v Lymanově sérii ležící v této oblasti. Když budeme počítat přeskoky mezi základní hladinou a dalšími vyššími hladinami, vždy dostaneme ještě vyšší energii (hladiny jsou dále od sebe) a daná čára bude vždy ležet v ultrafialové oblasti.
Vlnová délka fotonu při přeskoku mezi prvním a druhým excitovaným stavem (\(n=3\) a \(m=2\)) je \(\lambda_{32}=656{,}1\ \mathrm{nm}\). To je červená čára ve viditelné oblasti vodíkového spektra označovaná jako Hα. Jde o základní čáru ve viditelné Balmerově sérii. Čára mezi hladinami \(n=4\) a \(m=2\) je opět viditelná, \(\lambda_{42}=486{,}3\ \mathrm{nm}\), je to čára Hβ. I další dvě čáry této série jsou viditelné. Naproti tomu u více od sebe vzdálených hladin se již dostáváme do ultrafialové oblasti. Proto ve viditelné části spektra atomu vodíku nalezneme pouze čtyři emisní čáry.
Následující série se jmenuje Paschenova a odpovídá všem přeskokům do druhého excitovaného stavu (\(m=3\)). První čára z této série má vlnovou délku \(\lambda_{43}=1876{,}9\ \mathrm{nm}\) a leží, stejně jako všechny ostatní čáry nepříliš od sebe vzdálených hladin, v infračervené oblasti spektra.
Porovnejte vaše výsledky s hodnotami v obrázku 25.29.
Na následujícím obrázku je znázorněn energetický diagram atomu vodíku. Všimněte si, že vypočtené hodnoty jednotlivých spektrálních čar přesně odpovídají naměřeným hodnotám. Bohrův model umožňoval teoreticky vypočítat pozorované hodnoty vlnových délek spektrálních čar ve spektru atomu vodíku.
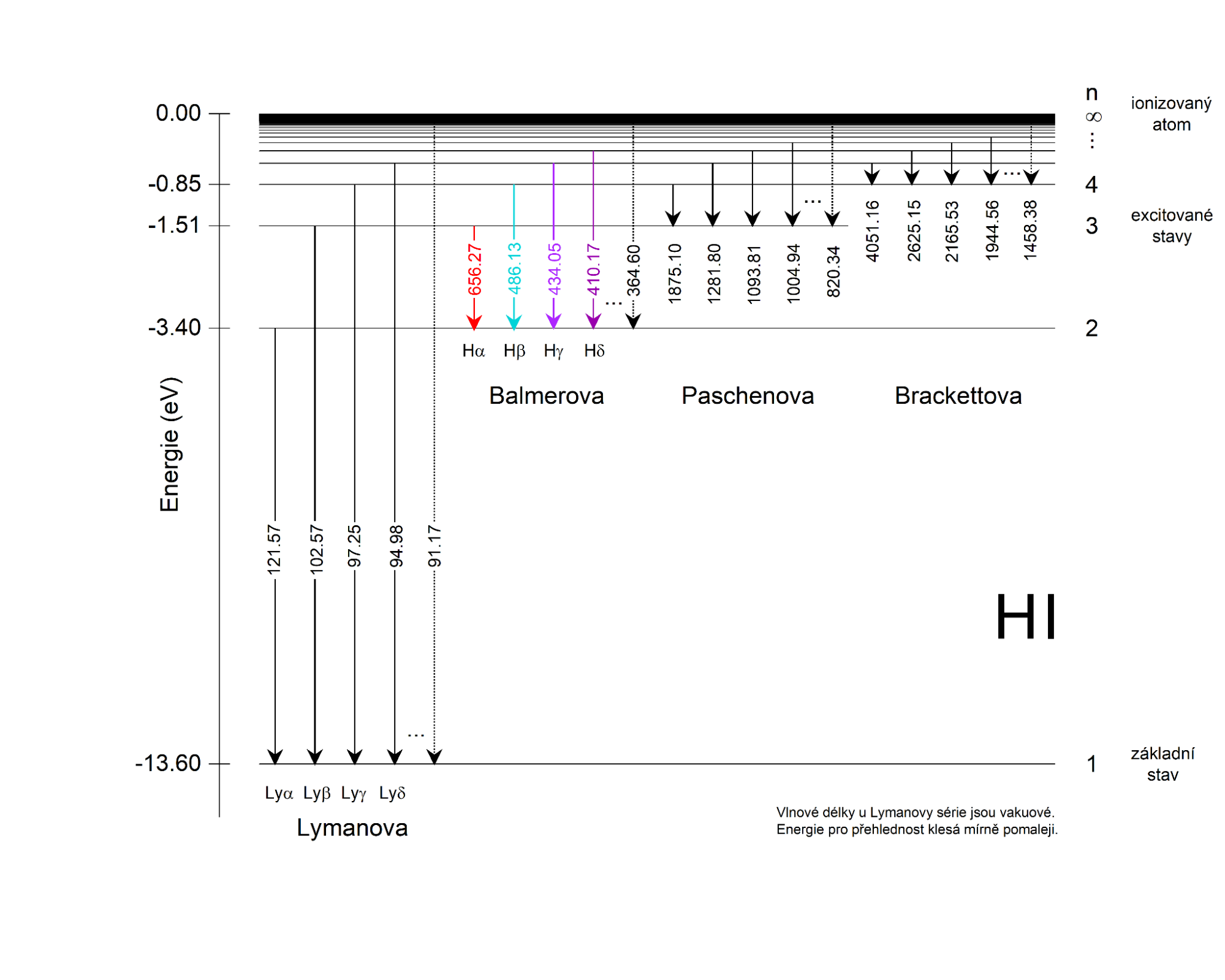
Zdroj
Atom vodíku je z hlediska matematického popisu velmi jednoduchý. V jeho elektronovém obalu se nachází jeden elektron, který se sice může vyskytovat v různých diskrétních vzdálenostech od jádra, přesto můžeme tyto energetické hladiny atomu stručně popsat pomocí matematických vzorců.
V případě dalších atomů, které mají větší množství elektronů, je takové energetické schéma podstatně složitější.
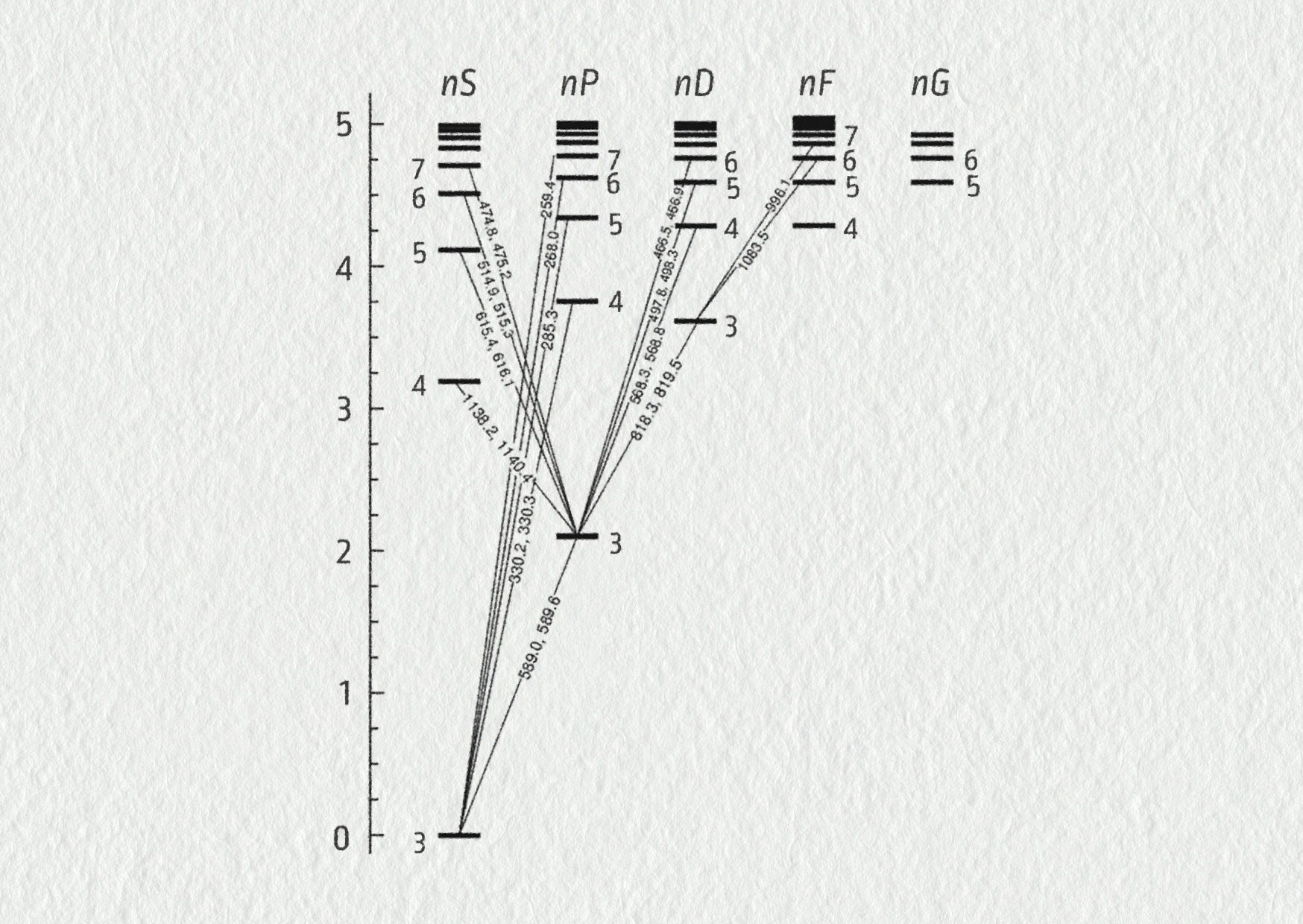
Zdroj
Přesto i zde platí: Jakýkoliv přeskok elektronu mezi dvěma energetickými hladinami je doprovázen buď emisí, nebo absorpcí záření, pro jehož vlnovou délku existuje vztah \(E=hf_{nm}=E_n-E_m\). Každý atom má svůj vlastní a jedinečný energetický diagram a jemu odpovídající spektrum.

Zdroj

