V této kapitole jsme se seznámili s několika experimenty, jejichž vysvětlení je možné pouze pomocí částicové povahy světla. Z předchozí kapitoly však známe jiné pokusy, které ke svému objasnění vyžadují vlnovou povahu světla.
Nabízí se logická otázka: Jaká je skutečná podstata světla? Možná vás to překvapí, ale na tuto otázku nedává fyzika jednoznačnou odpověď. Ukázalo se, že jevy spojené s vyzařováním a pohlcováním světla lze vysvětlit pomocí částicového modelu. Naopak pro šíření světla prostorem je vyhovujícím modelem vlnová teorie. Setkáváme se s formulací, že světlo má duální charakter. To znamená, že se někdy projevuje jako vlna, jindy zase jako proud částic.
Ve stejném roce, kdy Compton objasnil interakci RTG záření a volných elektronů, přišel francouzský fyzik Louis de Broglie s převratnou hypotézou. Světlo, na které jsme dříve nahlíželi jako na vlnění, se v některých případech chová jako částice. Co když to platí i opačně? Co když mikroobjekty, na které jsme dosud nahlíželi jako na částice, se někdy chovají jako vlny? De Broglie dokonce navrhl, jak určit vlnovou délku částice, která se pohybuje rychlostí \(v\):
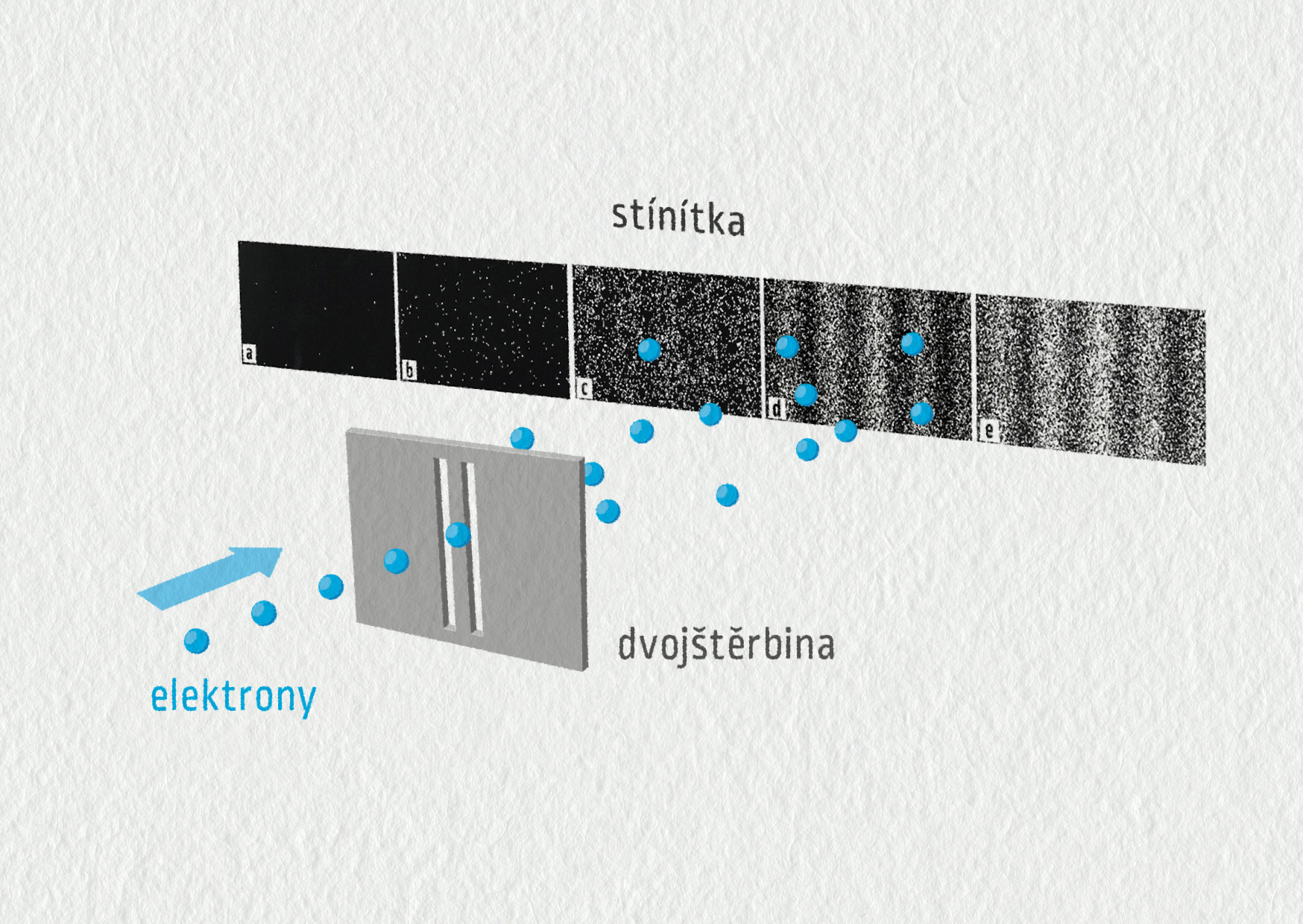
\[ \lambda = \frac hp = \frac{h}{mv}\;. \]Veličina p v předcházejícím výrazu je součin hmotnosti m a rychlosti v částice. Nazývá se hybnost. Fyzikové provedli zdánlivě jednoduchý pokus, při kterém nechali elektrony procházet dvojštěrbinou, podobně jako světlo. Po průchodu bylo místo dopadu jednotlivých elektronů zaznamenáno pomocí speciální vrstvy, která mění energii elektronu na světlo (viz obrázek).
Zdroj
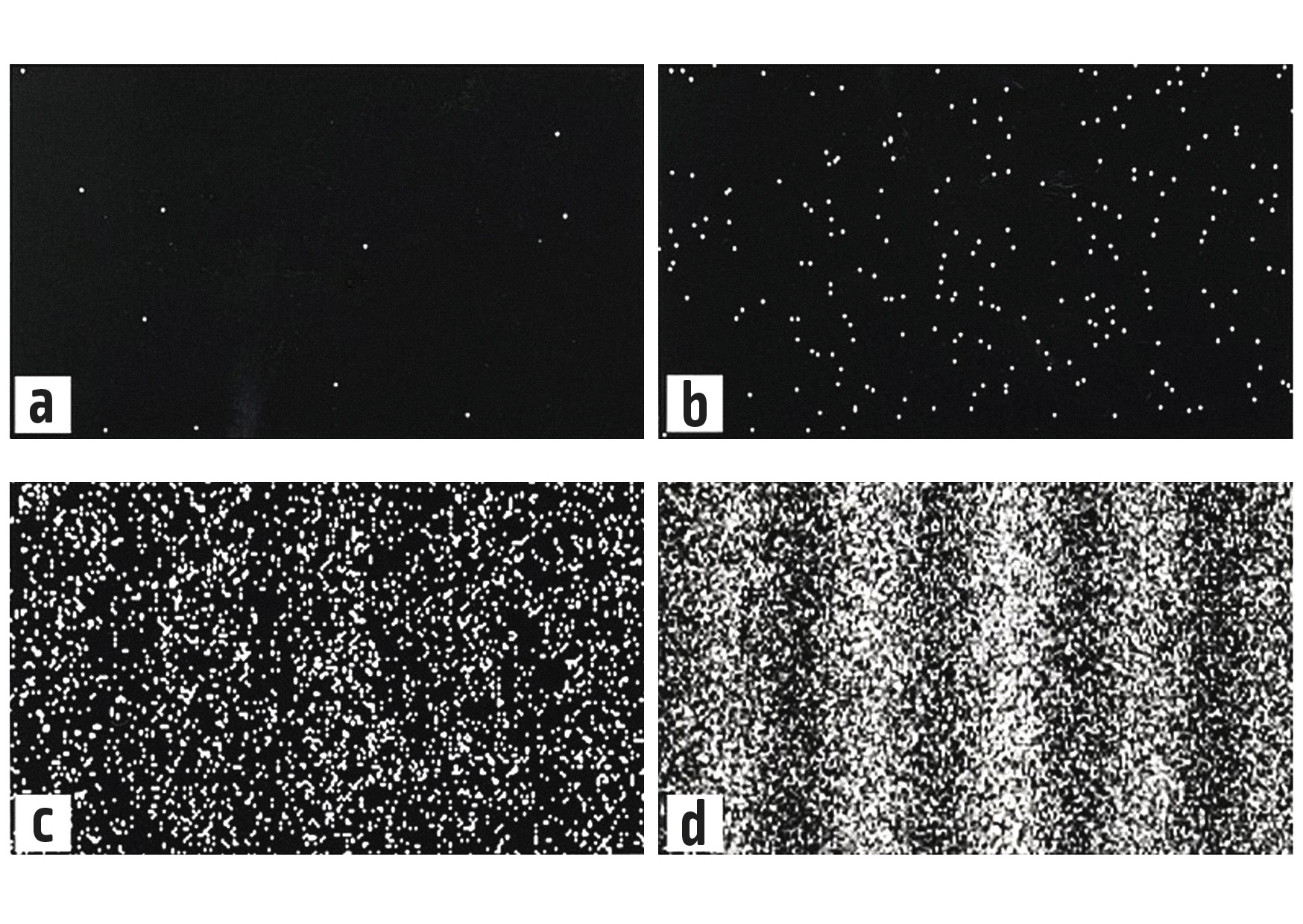
Ze začátku, kdy na citlivou vrstvu dopadne pouze prvních několik elektronů, se zdá, že jejich poloha je zcela náhodná. Avšak jakmile je jejich množství velké, začneme rozeznávat známý obrazec, jako by šlo o interferenci světla.
Zdroj
Na své cestě prostorem se tedy elektron chová jako vlna. Někdy se říká, že elektron „interferuje sám se sebou“, což ale není přesné, protože v tu chvíli se nejedná o částici. Na citlivé vrstvě už ale bez problémů pozorujeme konkrétní místo dopadu elektronu – částice!
Jaká je de Broglieho vlnová délka elektronu o energii 10,0 eV?
Nejprve vyjádříme hybnost elektronu \(p=mv\). Za rychlost dosadíme ze vztahu pro kinetickou energii \(v=\sqrt{2E_\mathrm{k}/m}\). Dostáváme tak
\[ p = m\sqrt{\frac{2E_\mathrm{k}}m} = \sqrt{2E_\mathrm{k}m}\;. \]De Broglieho vlnová délka elektronu má hodnotu
\[ \lambda = \frac{h}{\sqrt{2E_\mathrm{k}m}} = \frac{6{,}63\cdot10^{-34}}{\sqrt{2\cdot10{,}0\cdot1{,}602\cdot10^{-19}\cdot9{,}1\cdot10^{-31}}} = 3{,}88\cdot10^{-10}\ \mathrm{m} = 0{,}388\ \mathrm{nm}\;. \]Tato vlnová délka odpovídá rozměrům atomu nebo molekuly. Vlnové vlastnosti částic se tedy projevují v rozměru atomů. Toho využíváme, když urychlenými elektrony ozařujeme povrch krystalu a ze vzniklého difrakčního obrazce dokážeme určit rozložení jednotlivých atomů v krystalu.

Zdroj
Pro porovnání ještě vypočítejme de Broglieho vlnovou délku padajícího jablka. Uvažujme hmotnost 130 g a rychlost 5 m/s. Dosazením získáme
\[ \lambda = \frac hp = \frac{h}{mv} = \frac{6{,}63\cdot10^{-34}}{0{,}130\cdot5} = 1{,}0\cdot10^{-33}\ \mathrm{m}\;. \]Tato vlnová délka je o mnoho desítek řádů menší než rozměr atomu, a proto vlnové vlastnosti padajících jablek nemůžeme pozorovat.
Nejen světlo, ale ani další částice mikrosvěta se zkrátka nechovají jako předměty běžné denní potřeby, kterým bychom pouze zmenšili rozměry. Počínají si velmi podivně a představit si je jednoduše není v našich silách. Naštěstí fyzika dokáže pracovat i s tím, co si nedokážeme představit. Víme, že fyzika popisuje svět pomocí modelů a teorií. Zde jsme narazili na oblast, kde klasické teorie (vlnová i částicová) selhaly, a proto bylo potřeba vytvořit úplně novou teorii – kvantovou fyziku.
Mikroobjekty nejsou ani klasickými částicemi, ani vlněním. Jediný způsob, jak si je „představit“, je ponořit se do studia kvantové fyziky… Niels Bohr kdysi řekl: „Kdo není při setkání s kvantovou teorii šokován, ten ji zcela určitě nepochopil.“ Měl tím na mysli právě onu „rozpolcenost“ mezi částicovou a vlnovou povahou hmoty.

