Možná jste si všimli, že v předchozích příkladech jsme propočítávali obvody jen s jedním zdrojem a spotřebiče jsme nahrazovali rezistory. Co když je v obvodu více zdrojů, co když spotřebiče, jako např. žárovka a dioda, mají nelineární charakteristiky, a Ohmův zákon pro ně neplatí?
Nejuniverzálnějším nástrojem k řešení elektrických obvodů jsou Kirchhoffovy zákony. Jsou matematickým zápisem zákona zachování náboje a zákona zachování energie v elektrických obvodech. Lze je použít pro všechna zapojení.
1. Kirchhoffův zákon
Součet proudů vtékajících do uzlu je roven součtu proudů z uzlu vytékajících.
\[ \sum I_\mathrm{do} = \sum I_\mathrm{ven} \]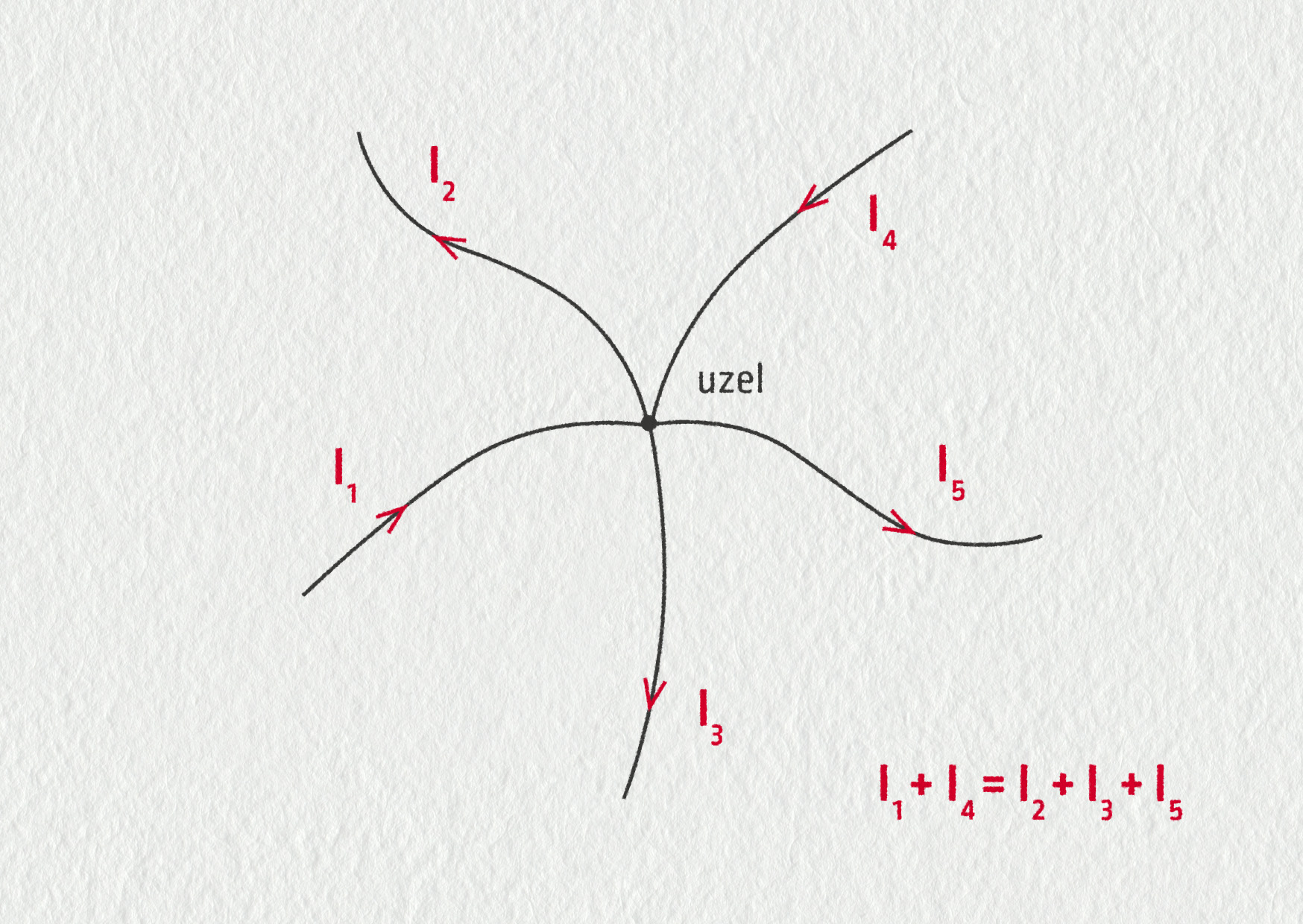
Zdroj
Platí pro libovolný uzel rozvětveného obvodu a vyjadřuje zákon zachování elektrického náboje.
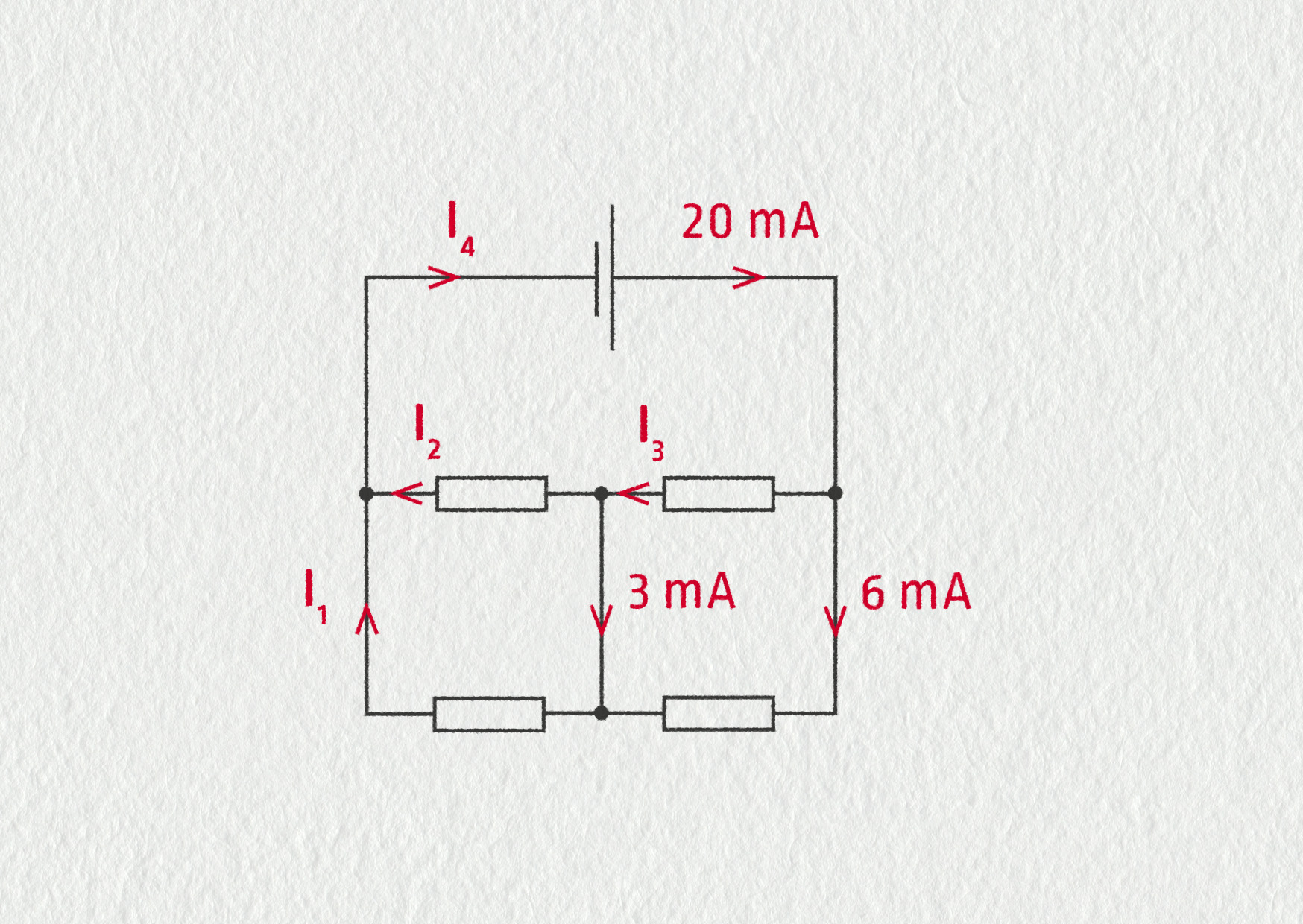
Zdroj
V obvodu 8.48 jsme změřili některé proudy. Pomocí 1.KZ dopočítejte proudy ve zbývajících větvích obvodu. Zapište hodnotu proudu v miliampérech.
2. Kirchhoffův zákon
V uzavřené smyčce je součet napětí na zdrojích roven součtu napětí na spotřebičích.
\[ \sum U_\mathrm{zdroje} = \sum U_\mathrm{spotřebiče} \]Platí pro libovolnou smyčku v obvodu.
Nejjednodušším příkladem uzavřené smyčky je obyčejný sériový obvod. Obecně vzato, uzavřená smyčka je jakákoli cesta, jak se větvemi obvodu dostat do výchozího místa. V následujícím schématu vidíte část nějaké velmi složité sítě a v ní jsou vyznačeny dvě různé smyčky. Každé smyčce odpovídá jedna rovnice mezi elektrickými veličinami.

Zdroj
Třebaže zápis 2. Kirchhoffova zákona vypadá jednoduše, při jeho používání musíme být pozorní na znaménka. Ukažme si „návod na použití“ nejprve obecně, potom na příkladu.
- V jednotlivých větvích označíme směr proudu. Pokud není zřejmé, jakým směrem teče ve skutečnosti, jeden směr si prostě zvolíme… a když jsme se volbou netrefili, vyjde nám záporná hodnota \(I\).
- Vybereme si nějakou smyčku a v ní si zvolíme směr obcházení.
- Do levé strany rovnice dosazujeme elektromotorická napětí na zdrojích: pokud by zdroj (uvažovaný samostatně, bez ohledu na zbytek obvodu) dával proud ve směru obcházení po smyčce, bereme jeho elektromotorické napětí jako kladné; je-li zdroj zapojen obráceně, jeho napětí dosazujeme se znaménkem minus.
- Do pravé strany rovnice dosazujeme napětí na spotřebičích: pokud daným spotřebičem teče proud ve směru obcházení po smyčce, bereme jeho napětí jako kladné; v opačném případě záporné.
Poznámka: Pokud smyčka obsahuje reálný zdroj (s vnitřním odporem), schéma překreslíme a tento zdroj znázorníme jako sériovou kombinaci ideálního zdroje (s napětím Ue) a vnitřního odporu r (bereme jako spotřebič) – viz Zdroje napětí.
Akumulátor o elektromotorickém napětí 10 V a vnitřním odporu 2 Ω připojíme k nabíječce dávající napětí 13 V s vnitřním odporem 1 Ω. Vypočítejte nabíjecí proud.

Zdroj
Obvod překreslíme pomocí ideálních zdrojů a vnitřních odporů. Označíme si zadané veličiny. Nabíječka dává vyšší napětí, určuje tedy směr proudu \(I\).
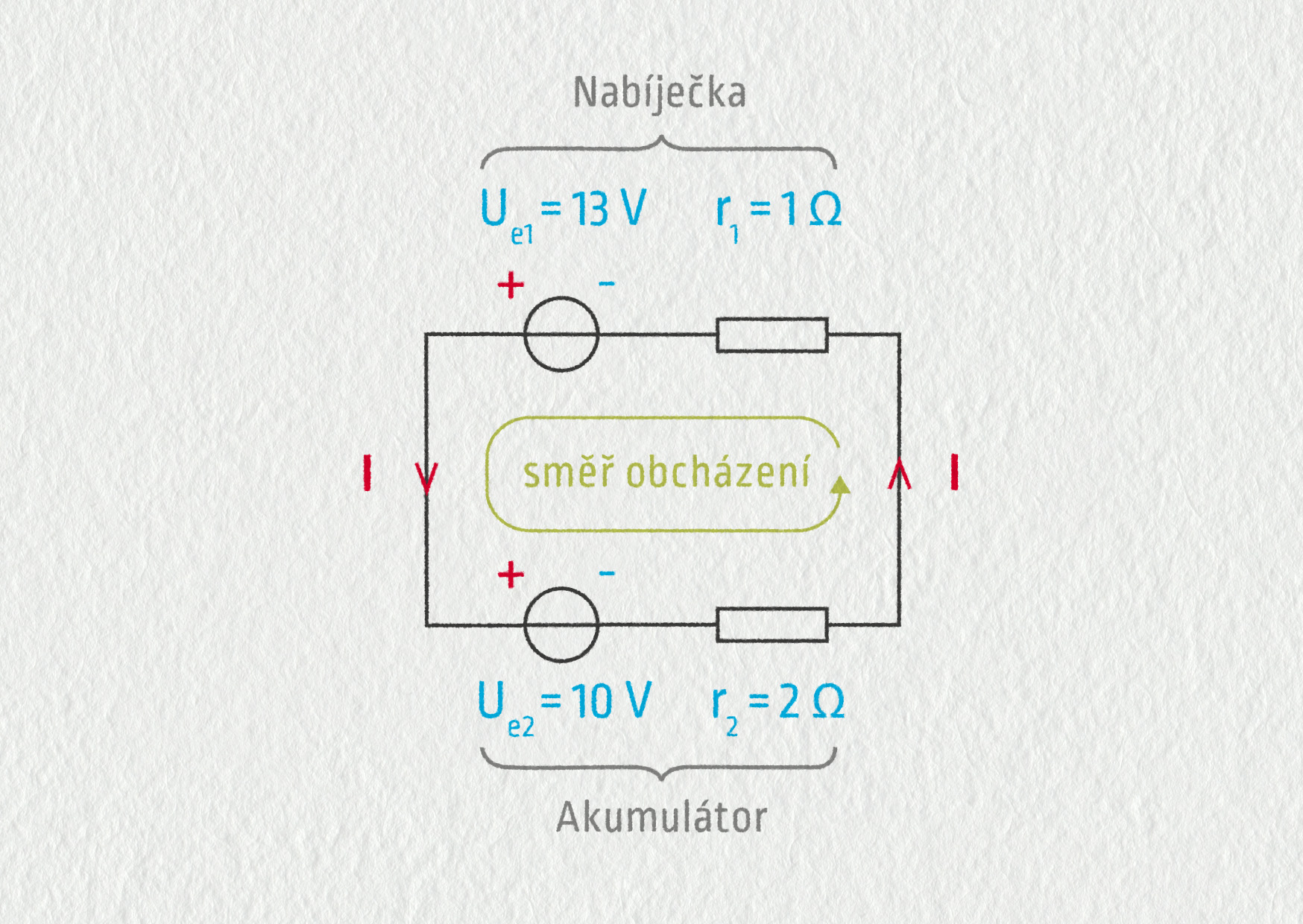
Zdroj
Směr obcházení po smyčce si zvolíme stejný, jako je předpokládaný směr proudu. Ve smyčce jsou dva zdroje (\(U_{\mathrm{e}1}\) a \(U_{\mathrm{e}1}\)) a dva spotřebiče (\(r_1\) a \(r_2\)). Dosadíme do 2. Kirchhoffova zákona:

Zdroj
Napětí na vnitřních odporech počítáme podle Ohmova zákona:
\[ U_{\mathrm{e}1} - U_{\mathrm{e}2} = r_1 I + r_2 I \] \[ I = \frac{U_{\mathrm{e}1} - U_{\mathrm{e}2}}{r_1 + r_2} = \frac{13-10}{1+2}\ \mathrm{A} = 1\ \mathrm{A} \]Při nabíjení teče proud 1 A.
Poznámka 1: Kdybychom si zvolili opačný směr obcházení po smyčce, bude první rovnice vynásobena minus jedničkou – zkuste to! Na závadu to není, násobení rovnice −1 je ekvivalentní úprava. 🙂
Poznámka 2: Kdybychom neuhodli správně směr proudu, žádná tragédie 🙂 , proud \(I\) vyjde stejně velký s opačným znaménkem – zkuste to!
Vypočítejte napětí v obvodu na obrázku 8.53.
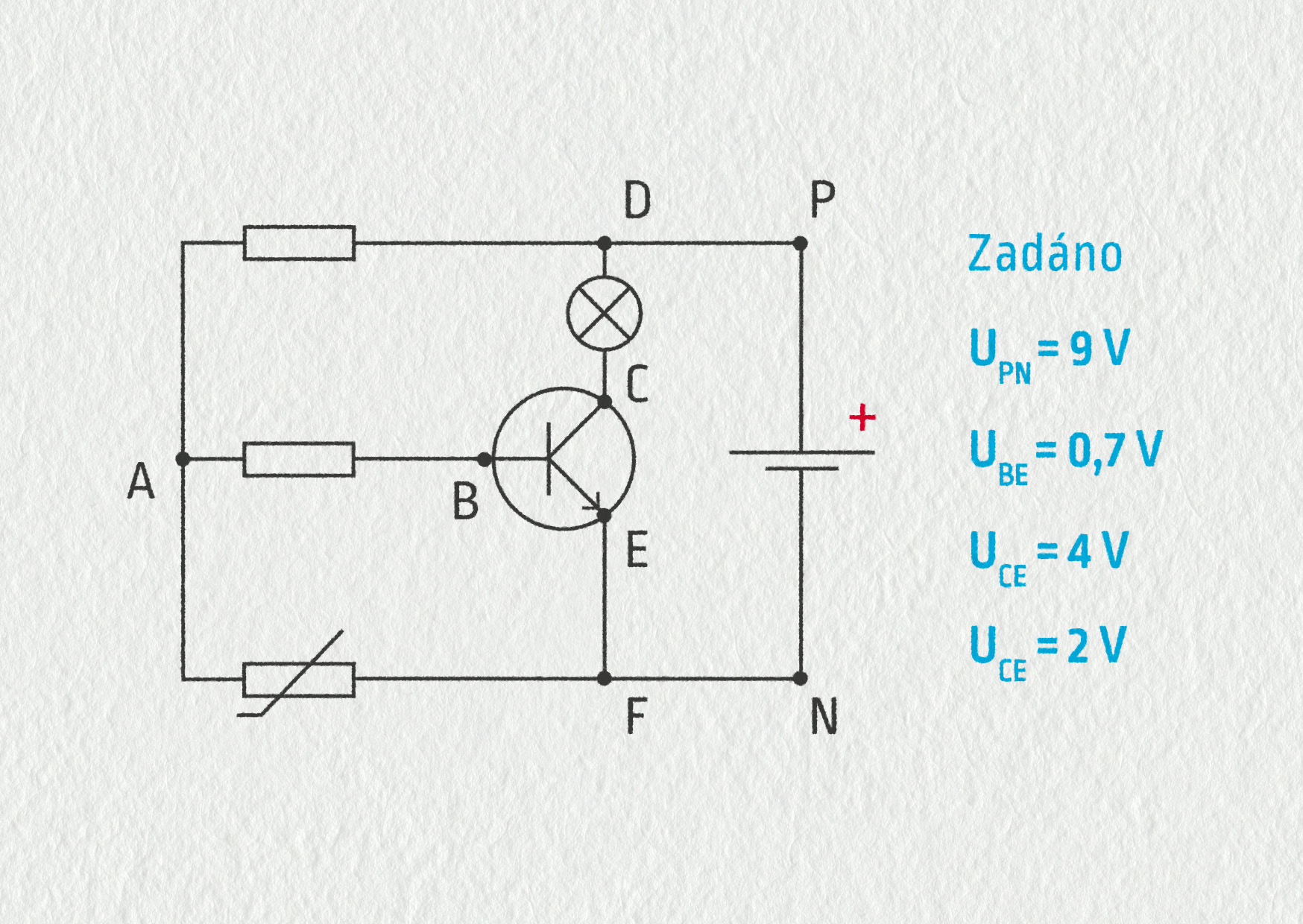
Zdroj
Zapište číselnou hodnotu ve voltech (V).
Vypočítejte proudy v jednotlivých větvích elektrické sítě na obrázku 8.54.
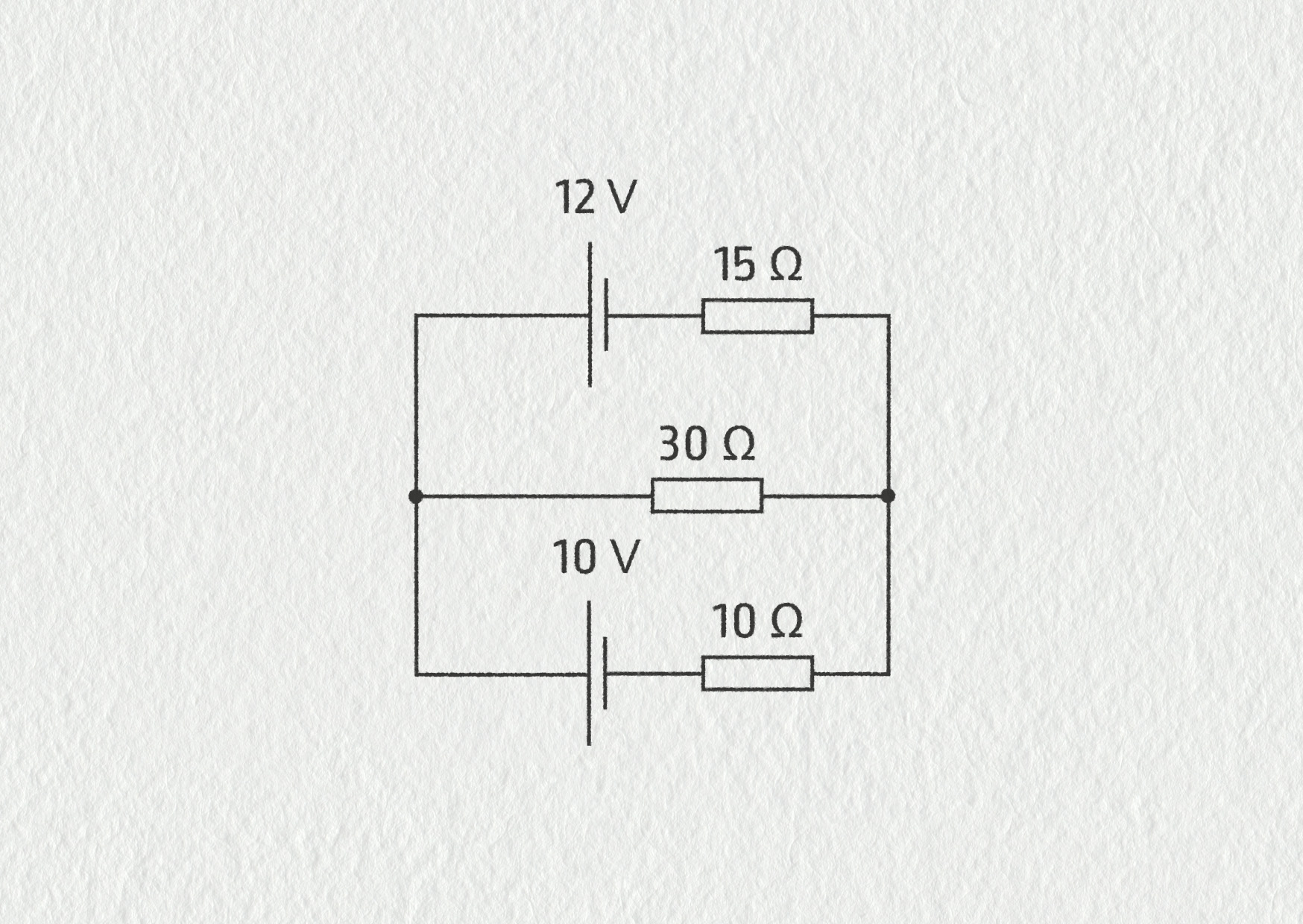
Zdroj
Označíme si zadané veličiny. Proudy ve větvích pojmenujeme a zkusíme uhodnout jejich směr – viz 2. poznámka v předchozím příkladu.
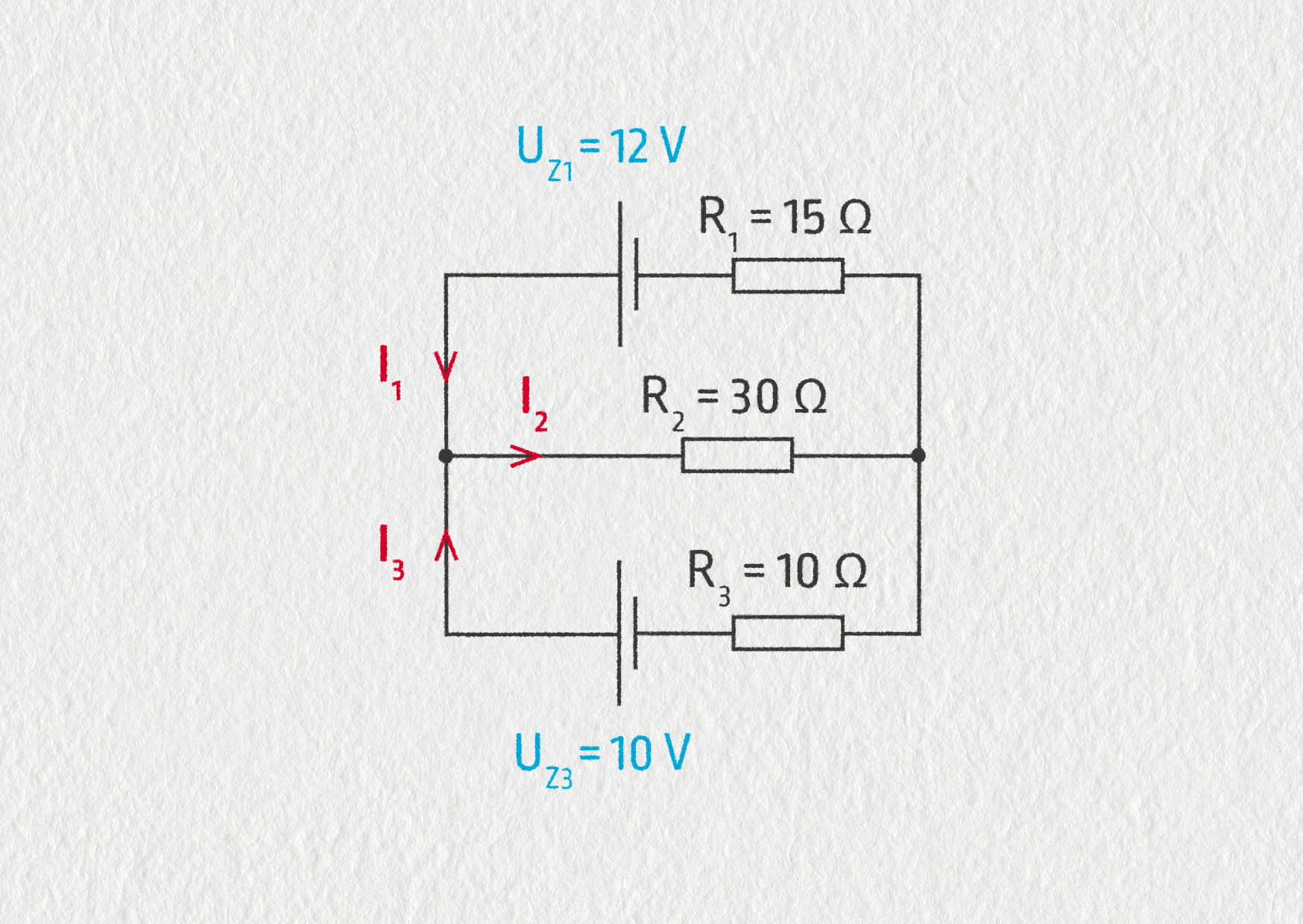
Zdroj
Máme tři neznámé proudy – potřebujeme sestavit soustavu tří rovnic pro tři neznámé. Z 1. Kirchhoffova zákona získáme první rovnici: \(I_1 + I_3 = I_2\). 1. KZ pro druhý uzel by nám dal tutéž rovnici, musíme tedy použít také 2. KZ.
Zvolíme si dvě smyčky – viz obrázek.
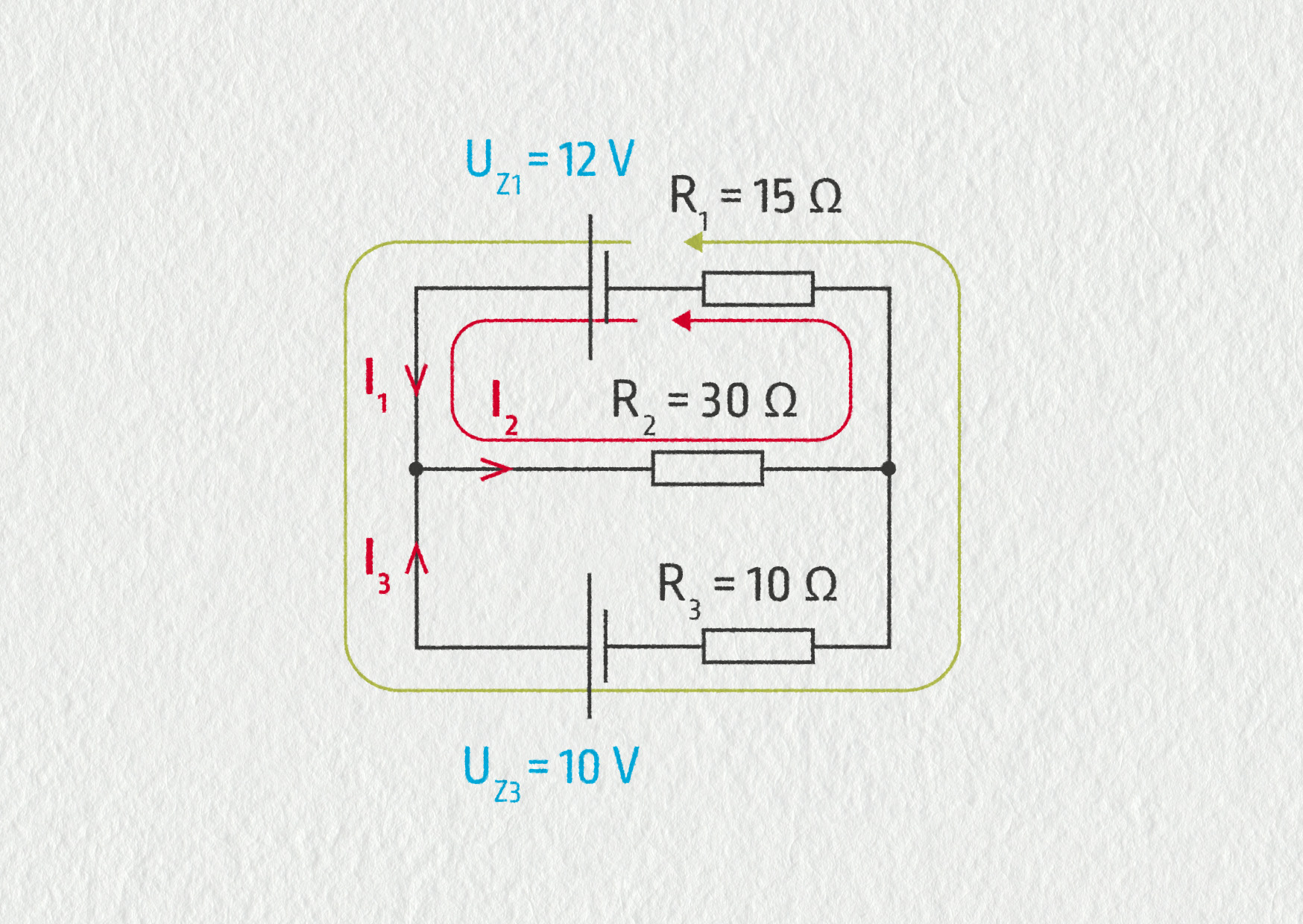
Zdroj
Červená smyčka: \(U_{\mathrm{Z}1} = R_1 I_1 + R_2 I_2\)
Zelená smyčka: \(U_{\mathrm{Z}1} - U_{\mathrm{Z}3} = R_1 I_1 - R_3 I_3\)
Po dosazení číselných hodnot získáme soustavu tří algebraických rovnic pro tři neznámé.
Řešením této soustavy jsou proudy \(I_1 = 0{,}2\ \mathrm{A}\), \(I_2 = 0{,}3\ \mathrm{A}\) a \(I_3 = 0{,}1\ \mathrm{A}\).
Poznamenejme, že správně bychom měli ke všem číselným hodnotám psát jednotky. Ovšem fyzikální vztahy mají tu pěknou vlastnost, že pokud do nich dosadíme v základních jednotkách, vyjde výsledek v základních jednotkách.

