Řešení elektrických obvodů spočívá nejčastěji v nalezení proudů v jednotlivých větvích a napětí na jednotlivých součástkách, jakmile jsou zdroje připojeny. Parametry jednotlivých součástek považujeme za známé.
V této předposlední části kapitoly nebude téměř žádná nová „teorie“, vše podstatné už známe z předchozího výkladu. Ukážeme si na několika příkladech, jak tyto poznatky používat.
Příklad 1: Výsledný odpor
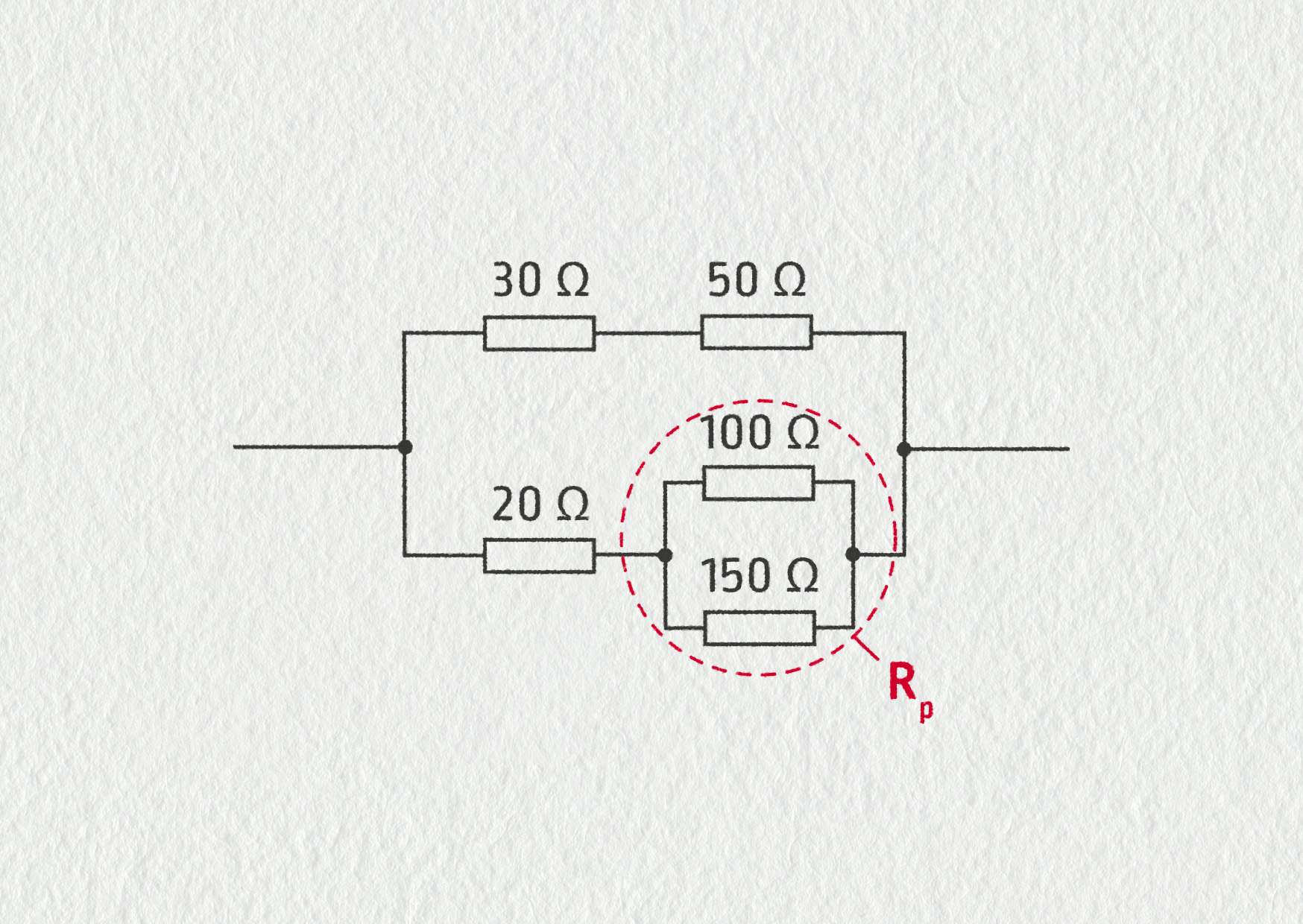
Určete celkový odpor kombinace rezistorů na obrázku 8.40.
Zdroj
Typická úloha z elektřiny, uvidíte v následujícím, k čemu se bude hodit.
Základní myšlenka: používáme pouze pravidla pro výsledný odpor sériového a paralelního zapojení, postupně zjednodušujeme zapojení tím, že kombinaci součástek nahradíme jejich celkovým odporem, začínáme vždy od nejvíce vnořených součástí zapojení.
Řešení
Odpory 100 Ω a 150 Ω jsou zapojeny paralelně:
\[ \frac{1}{R_\mathrm{p}} = \frac{1}{100\ \mathrm{\Omega}} + \frac{1}{150\ \mathrm{\Omega}} = \frac{1}{60\ \mathrm{\Omega}}\;,\]takže tato paralelní kombinace se chová jako jediný rezistor o odporu \(R_\mathrm{p}=60\ \mathrm{\Omega}\).
Zdroj
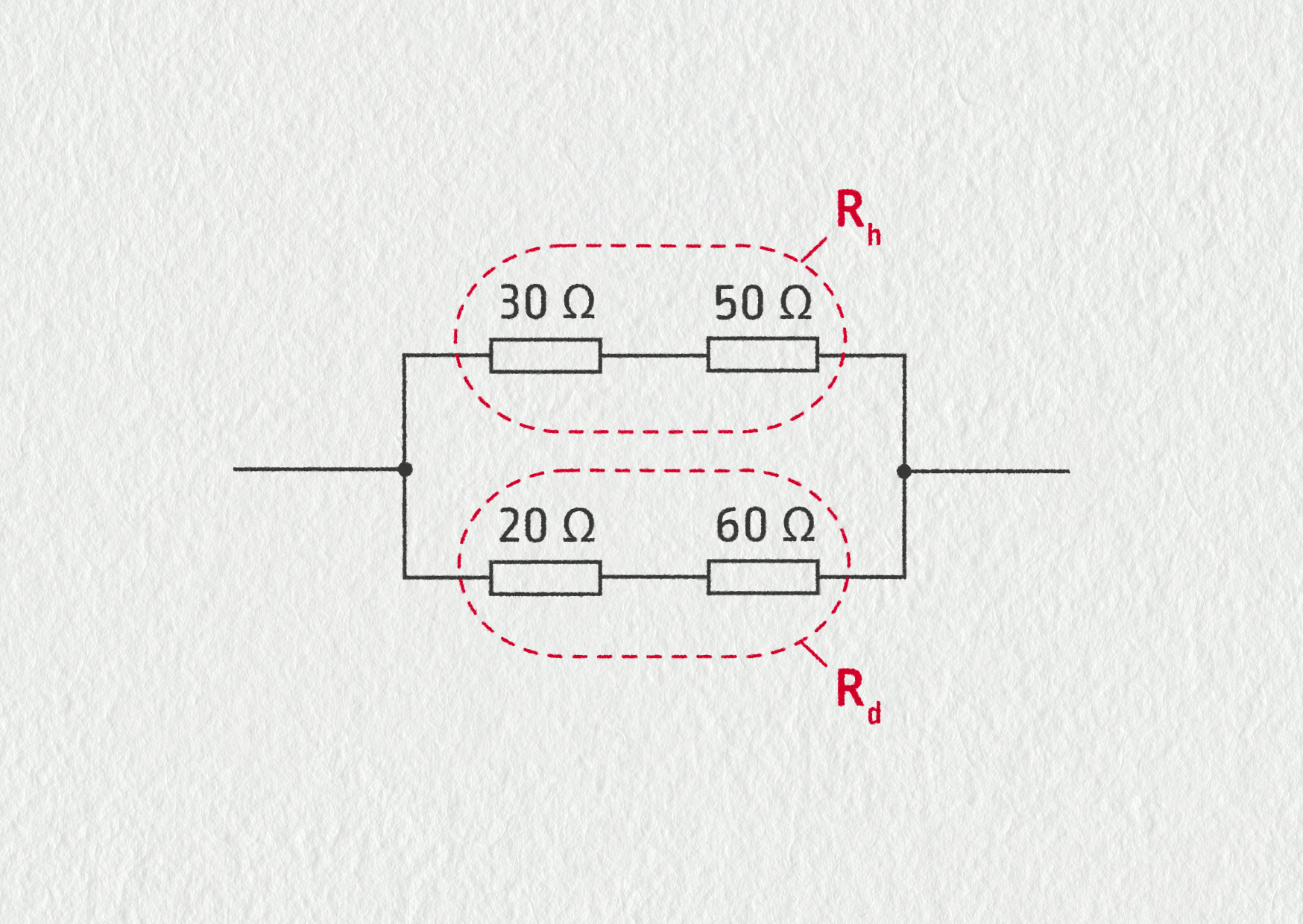
V horní větvi máme 30 Ω a 50 Ω sériově, takže odpor horní větve je \(R_\mathrm{h}=30\ \mathrm{\Omega}+50\ \mathrm{\Omega} = 80\ \mathrm{\Omega}\). V dolní větvi máme 20 Ω a 60 Ω sériově, takže odpor dolní větve \(R_\mathrm{d} = 20\ \mathrm{\Omega} + 60\ \mathrm{\Omega} = 80\ \mathrm{\Omega}\).
Zdroj
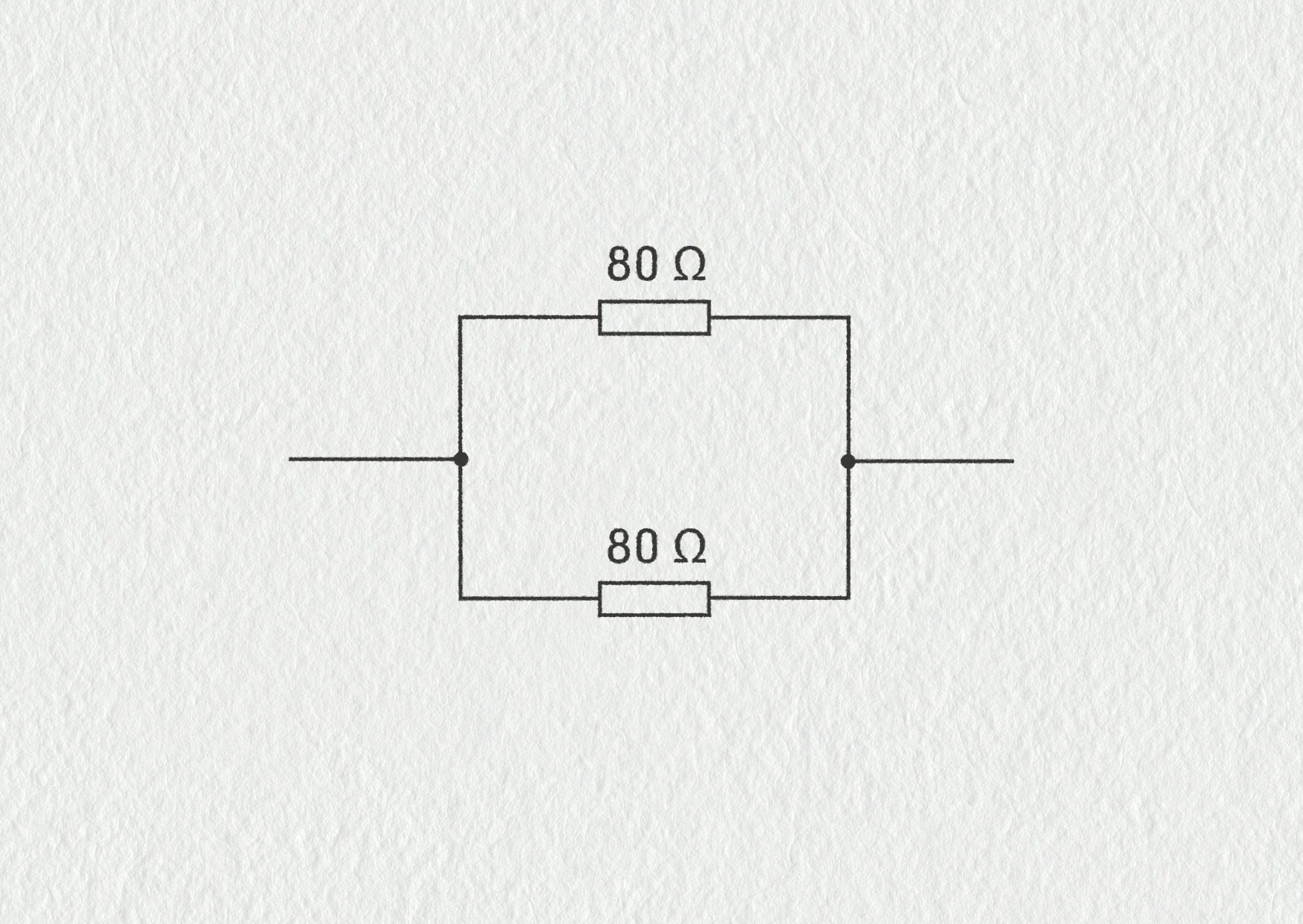
Horní a dolní větev jsou zapojeny paralelně, takže platí
\[ \frac{1}{R} = \frac{1}{R_\mathrm{h}} + \frac{1}{R_\mathrm{d}} = \frac{1}{80\ \mathrm{\Omega}} + \frac{1}{80\ \mathrm{\Omega}} = \frac{1}{40\ \mathrm{\Omega}}.\]Celkový odpor původního zapojení je 40 Ω.
Příklad 2: Ohmův zákon pro uzavřený obvod
Určete proud odebíraný ze zdroje v obvodu na obrázku 8.43.

Zdroj
Základní myšlenka: Používáme pravidla pro řazení rezistorů, vztah pro svorkové napětí zdroje a Ohmův zákon pro rezistor. Nejdříve si označíme hledaný proud. Nahradíme celý vnější obvod jediným výsledným odporem, napětí na zdroji je pak rovno napětí na tomto odporu. Z této rovnosti dopočítáme proud.
Řešení
Reálný zdroj si rozkreslíme jako sériové zapojení ideálního zdroje a vnitřního odporu.
Polarita zdroje určuje směr proudu: proud teče obvodem od kladného k zápornému pólu. Výsledný odpor \(R\): odpor dolní větve (rezistory v sérii) vypočítáme součtem \(10\ \mathrm{\Omega} + 20\ \mathrm{\Omega} = 30\ \mathrm{\Omega}\), celkový odpor určíme ze vztahu
\[ \frac{1}{R} = \frac{1}{15\ \mathrm{\Omega}} + \frac{1}{30\ \mathrm{\Omega}} = \frac{1}{10\ \mathrm{\Omega}}\;,\]takže \(R = 10\ \mathrm{\Omega}\). Čili celý vnější obvod se chová jako rezistor o odporu 10 Ω připojený do bodů A a B.
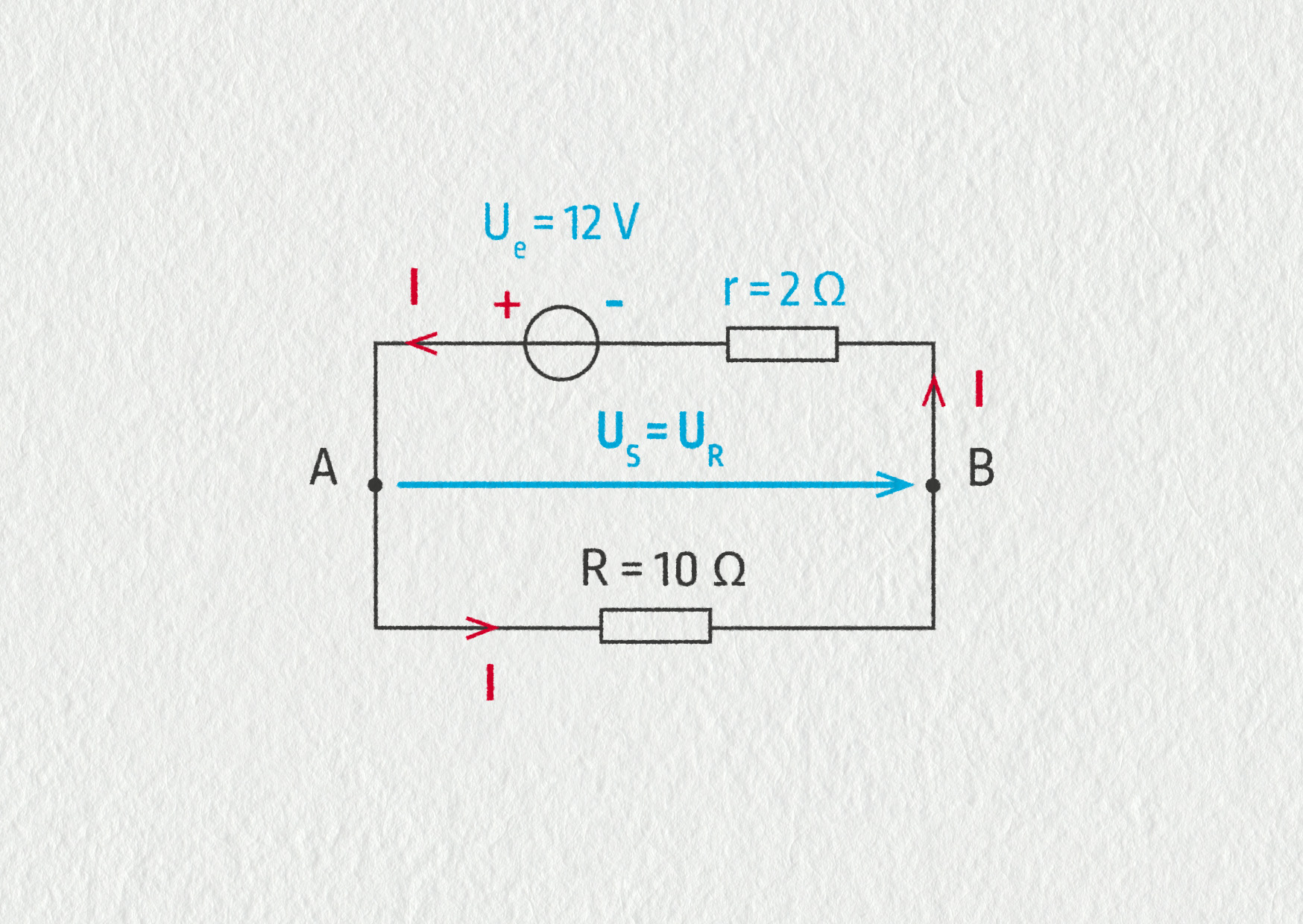
Zdroj
K těmto bodům je připojen i zdroj, takže napětí \(U_{AB} = U_\mathrm{S} = U_\mathrm{R}\). Napětí na svorkách reálného zdroje závisí na odebíraném proudu \(U_\mathrm{S} = U_\mathrm{e}-rI\). Napětí na rezistoru je podle Ohmova zákona \(U_\mathrm{R} = RI\). Dosazením dostáváme
\[ \begin{aligned} U_\mathrm{e}-rI &=RI\\ U_\mathrm{e} &= rI + RI\\ U_\mathrm{e} &= (r + R)\cdot I\\ I &= \frac{U_\mathrm{e}}{r + R} \end{aligned} \]Proud odebíraný ze zdroje se vypočítá jako elektromotorické napětí zdroje dělené součtem vnitřního odporu zdroje a celkového odporu vnějšího obvodu.
Číselně \(I = 12/(2 + 10)\ \mathrm{A} = 1\ \mathrm{A}.\)
Příklad 3: Rozvětvený obvod s rezistory a jedním zdrojem
Na obrázku 8.45 je obvod sestavený ze zdroje o elektromotorickém napětí \(U_\mathrm{e} = 12\ \mathrm{V}\) a vnitřním odporu \(r = 1\ \mathrm{\Omega}\) a ze tří rezistorů o odporech \(R_1 = 8\ \mathrm{\Omega}\), \(R_2 = 20\ \mathrm{\Omega}\), \(R_3 = 60\ \mathrm{\Omega}\). Určete pracovní bod obvodu, tj. proudy v jednotlivých větvích a napětí na jednotlivých součástkách.
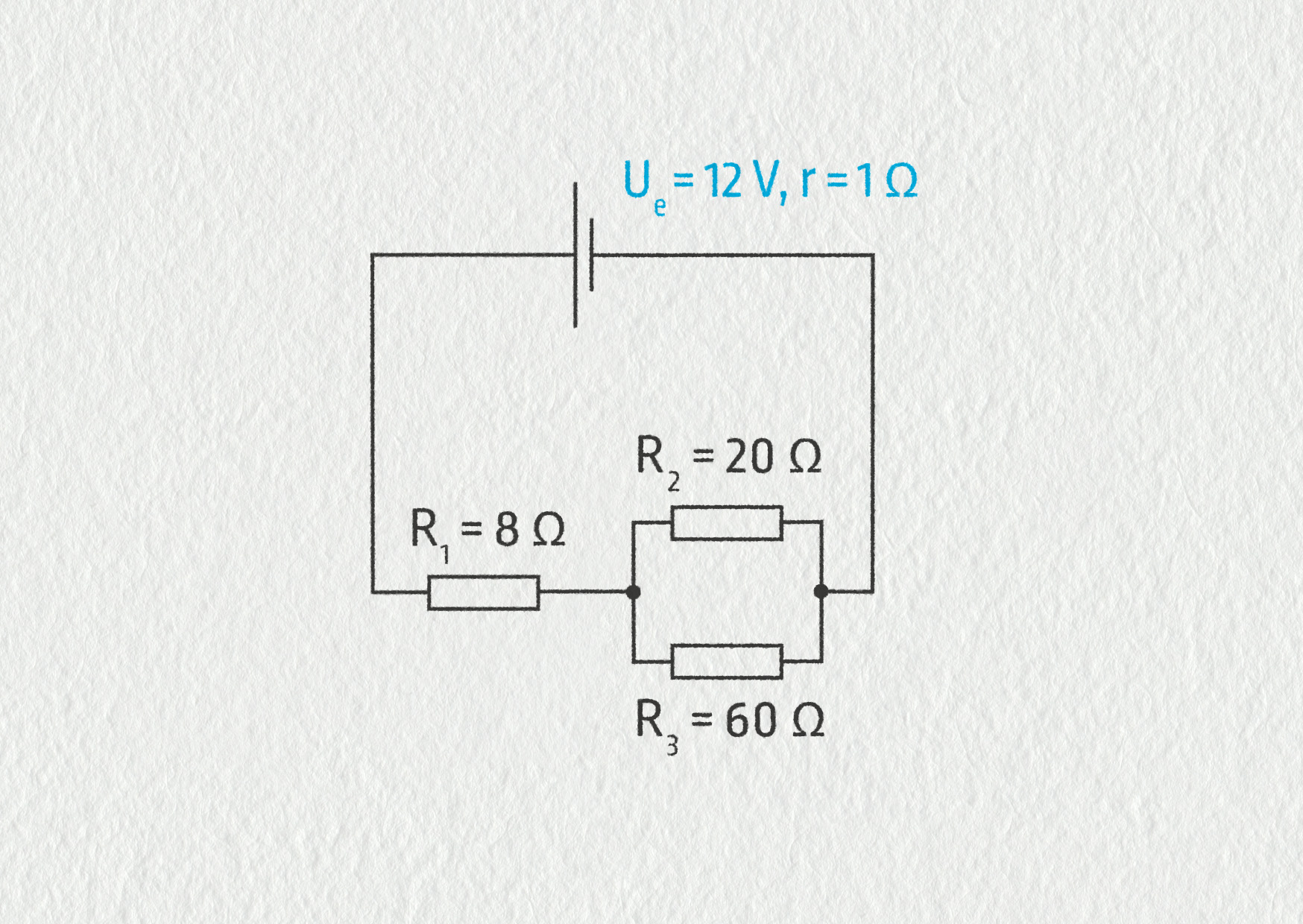
Zdroj
Řešení
Nejdříve si vyznačíme směry proudů v obvodu a označíme známé a hledané veličiny.
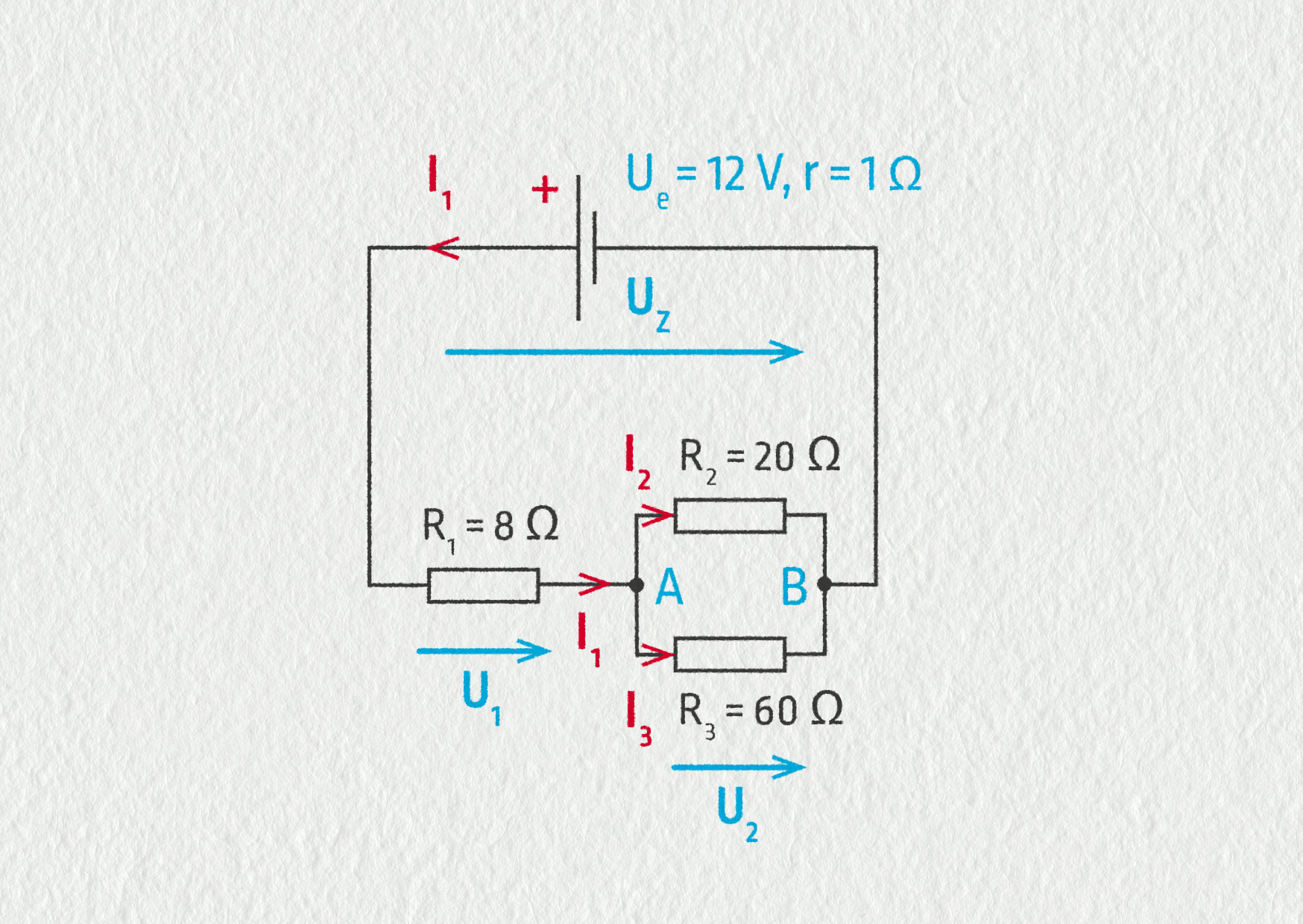
Zdroj
Proud \(I_1\) tekoucí zdrojem a rezistorem \(R_1\) spočítáme pomocí Ohmova zákona pro uzavřený obvod. Snadno ověříme, že celkový odpor obvodu je \(R = 23\ \mathrm{\Omega}\), takže
\[ I_1 = \frac{U_\mathrm{e}}{r + R} = \frac{12}{1 + 23}\ \mathrm{A} = 0{,}5\ \mathrm{A}\;. \]Odtud můžeme určit napětí na zdroji
\[ U_\mathrm{S} = U_\mathrm{e}-rI_1 = (12-1\cdot0{,}5)\ \mathrm{V} = 11{,}5\ \mathrm{V} \]a z Ohmova zákona pro rezistor napětí na prvním rezistoru \(U_1 = R_1I_1 = 8\cdot0{,}5 = 4\ \mathrm{V}\).
Z kapitoly o napětí víme, že pro libovolné tři body obvodu A, B, C platí \(U_{AC} = U_{AB} + U_{BC}\). Takže v našem obvodu \(U_\mathrm{S} = U_1 + U_2\), a proto \(U_2 = 11{,}5\ \mathrm{V}-4\ \mathrm{V} = 7,5\ \mathrm{V}\), což je zřejmě napětí na rezistoru 2 (stejné jako na rezistoru 3).
Rezistory \(R_2\) a \(R_3\) jsou připojeny k uzlům B a C a platí pro ně Ohmův zákon. Odtud získáme proudy
\[ I_2 = \frac{U_2}{R_2} = \frac{7{,}5}{20}\ \mathrm{A} = 0{,}375\ \mathrm{A} = 375\ \mathrm{mA} \]a
\[ I_3 = \frac{U_2}{R_3} = \frac{7{,}5}{60}\ \mathrm{A} = 0{,}125\ \mathrm{A} = 125\ \mathrm{mA} \]Tím je úloha vyřešena. Můžete se přesvědčit, že jsme počítali správně, součet \(I_2 + I_3\) dá skutečně \(I_1\) a poměr \(I_2 : I_3 = 3 : 1\), což je skutečně obrácený poměr odporů.

