V této podkapitole prozkoumáme vlastnosti dvou základních obvodů v elektřině.
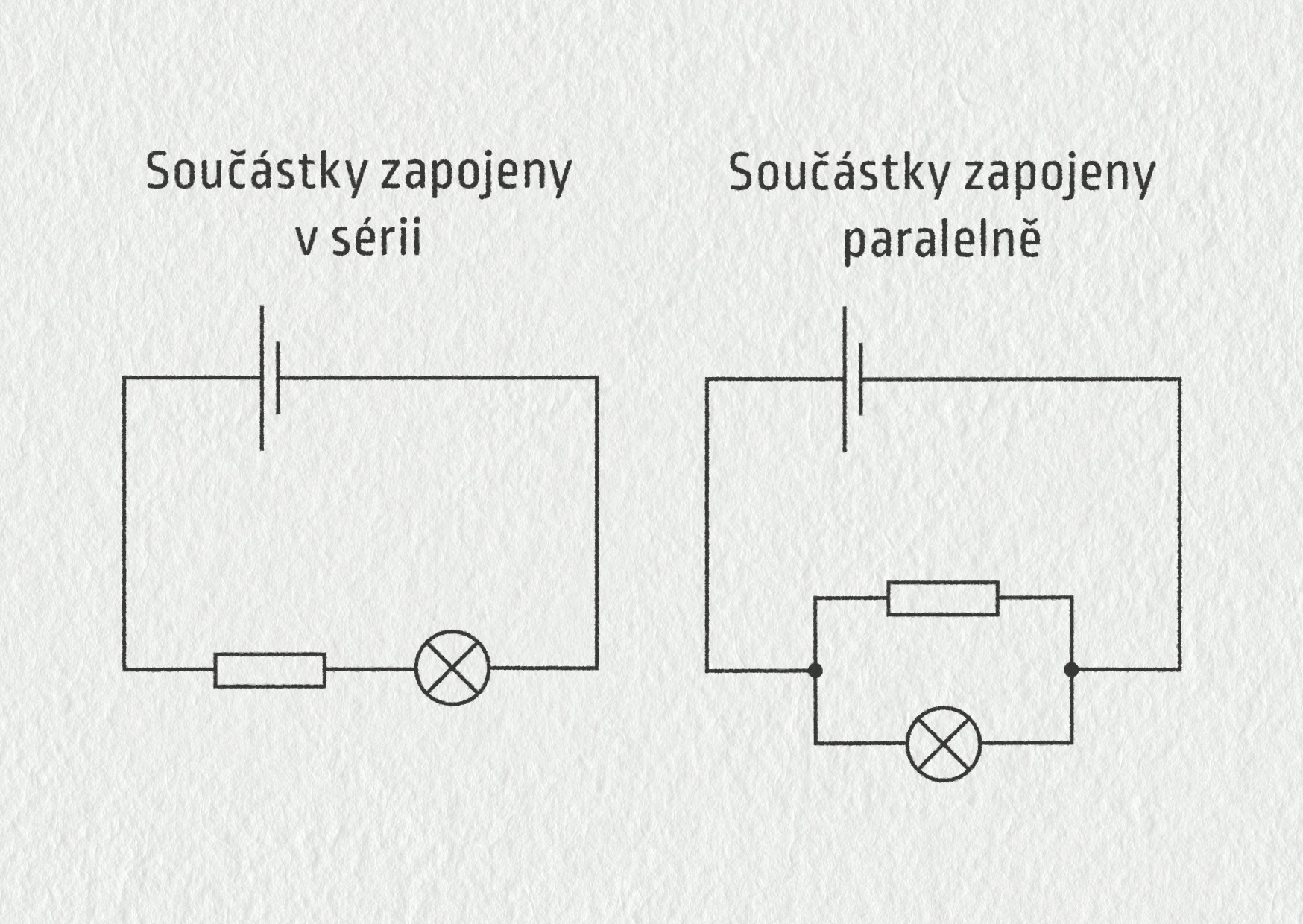
Sériový obvod nemá žádná větvení, součástky jsou zapojeny za sebou podobně jako vagóny ve vlaku.
Paralelní obvod obsahuje body větvení (uzly), součástky jsou zapojeny vedle sebe podobně, jako se drží tanečníci při valčíku.
Zdroj
Sériový obvod
Nejdůležitější zákonitosti sériového obvodu vysvětlíme na následujícím modelovém zapojení. Uvažujme obvod tvořený zdrojem konstantního napětí \(U_\mathrm{Z}\) a dvěma rezistory o odporech \(R_1\) a \(R_2\) zapojenými do série. Napětí na svorkách rezistorů označíme \(U_1\) a \(U_2\) – viz obrázek.
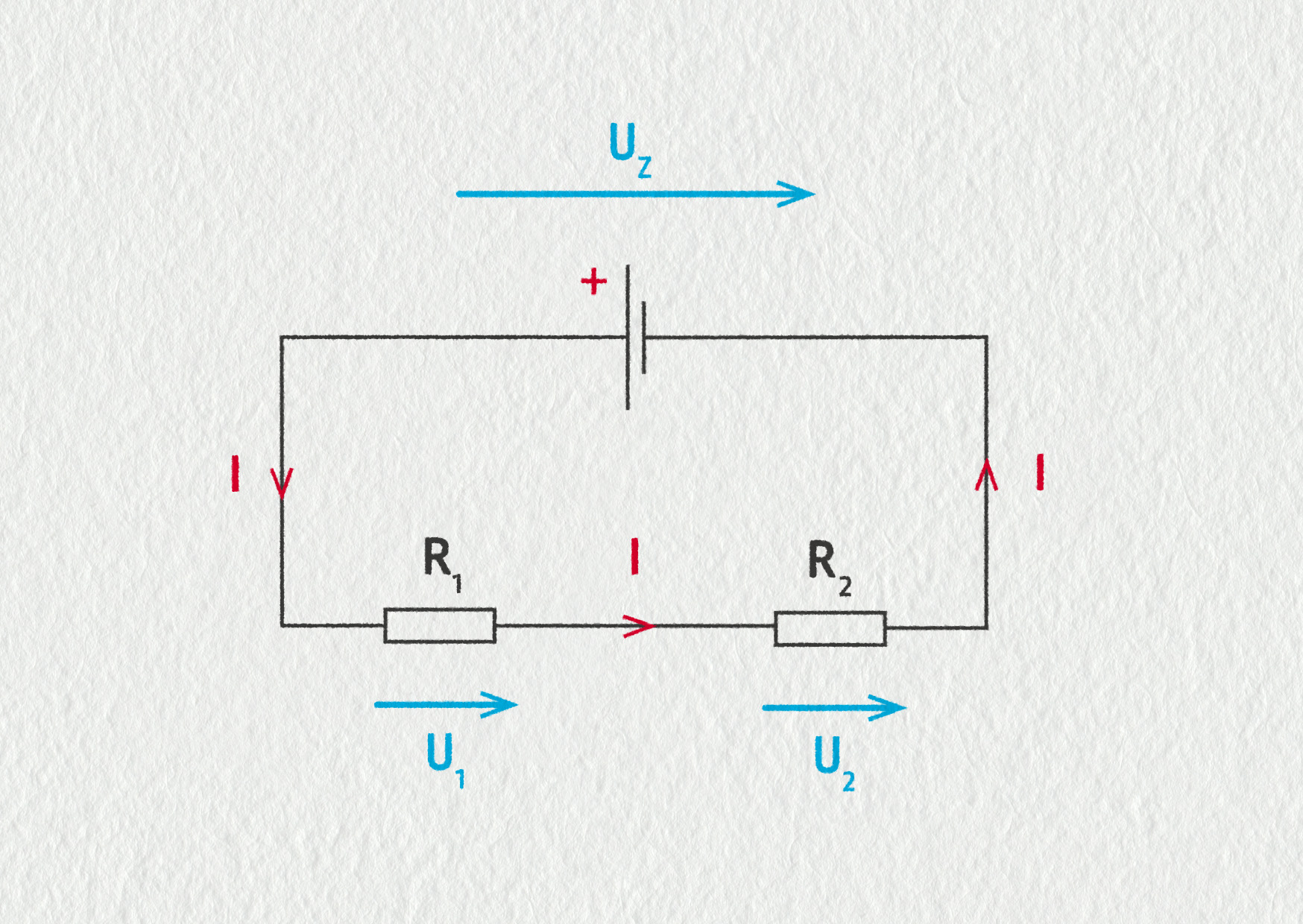
Zdroj
Pro elektrické veličiny platí:
- V sériovém obvodu protéká všemi součástkami stejný proud \(I\).
- Napětí na zdroji je rovno součtu napětí na spotřebičích, \(U_\mathrm{Z}=U_1+U_2\).
- Celkový odpor obvodu je roven součtu odporů na spotřebičích, \(R=R_1+R_2\).
- Poměr napětí na spotřebičích je stejný jako poměr jejich odporů, \(U_1/U_2=R_1/R_2\).
Odvození:
- V obvodu nejsou žádné body větvení. V součástkách náboj nevzniká ani nezaniká, takže proud, který na jedné straně do součástky vtéká, z ní na druhé straně vytéká. Vlastnost plyne přímo ze zákona zachování náboje.
- Označme si v obvodu body A, B, C. Zdroj je zapojen mezi body A a C, tedy \(U_\mathrm{Z}=U_{AC}\), podobně pro spotřebiče \(U_1=U_{AB}\), \(U_2=U_{BC}\). Z předchozí kapitoly 7.3 víme, že obecně platí \(U_{AC}=U_{AB}+U_{BC}\), takže \(U_\mathrm{Z}=U_1+U_2\). Tato vlastnost plyne ze zákona zachování energie v elektrických obvodech.
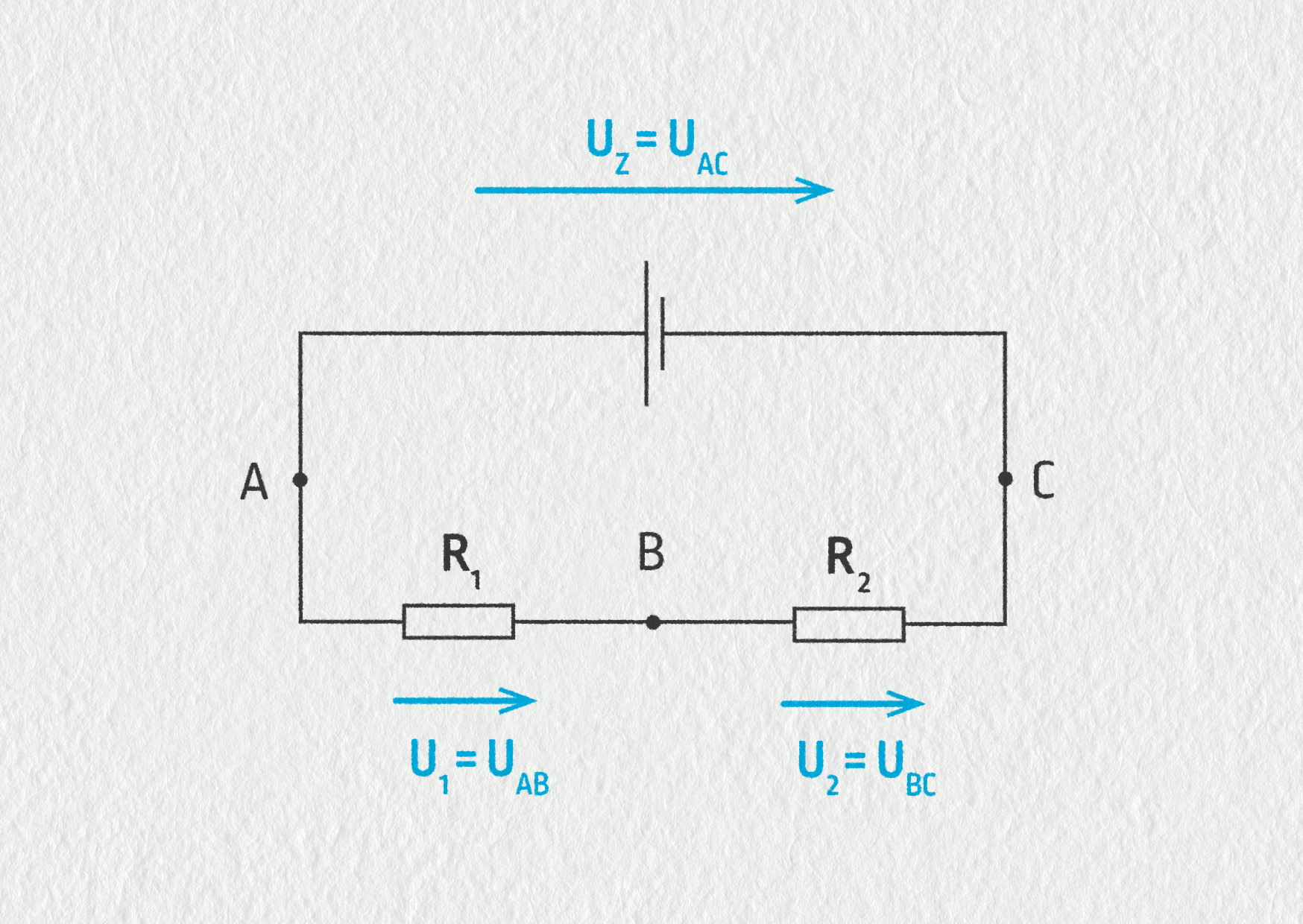
8.23 – K odvození vztahů pro sériový obvod
Zdroj - Použijeme Ohmův zákon: \(U_1=R_1I\) a \(U_2=R_2I\) (proud je podle (1) stejný, nemusíme indexovat). Dosadíme do (2): \(U_\mathrm{Z}=U_1+U_2=R_1I+R_2I=(R_1+R_2)I\), takže celkový odpor obvodu \(R=U_\mathrm{Z}/I=R_1+R_2\). Pokud by byl ve studovaném obvodu zapojen reálný zdroj s nenulovým vnitřním odporem, byl by celkový odpor obvodu součtem odporu spotřebičů a vnitřního odporu zdroje.
- Z Ohmova zákona pro oba spotřebiče vyjádříme proud: \(I=U_1/R_1\), \(I=U_2/R_2\). Jelikož je proud podle (1) stejný, platí \(U_1/R_1=U_2/R_2\), takže po úpravě \(U_1/U_2=R_1/R_2\).
K čemu jsou užitečné sériové obvody? Ukažme si to na příkladech.
Ochranný rezistor
Celkem běžná je situace, že máte zdroj vytvářející jiné napětí, než které spotřebič potřebuje ke své funkci. Vezmete-li například modrou LEDku, která dobře svítí při napětí 3,2 V a proudu 10 mA, nikdy se vám nerozsvítí jen pomocí tužkové baterie (1,5 V) – napětí je příliš nízké. Naopak k šestivoltovému akumulátoru LEDku připojit přímo nesmíte, neboť příliš vysoké napětí by vyvolalo v diodě příliš velký proud a dioda by se spálila Jouleovým teplem. Jak to vyřešit? Sestavíme sériový obvod s ochranným rezistorem a jeho odpor zvolíme tak, abychom splnili parametry diody
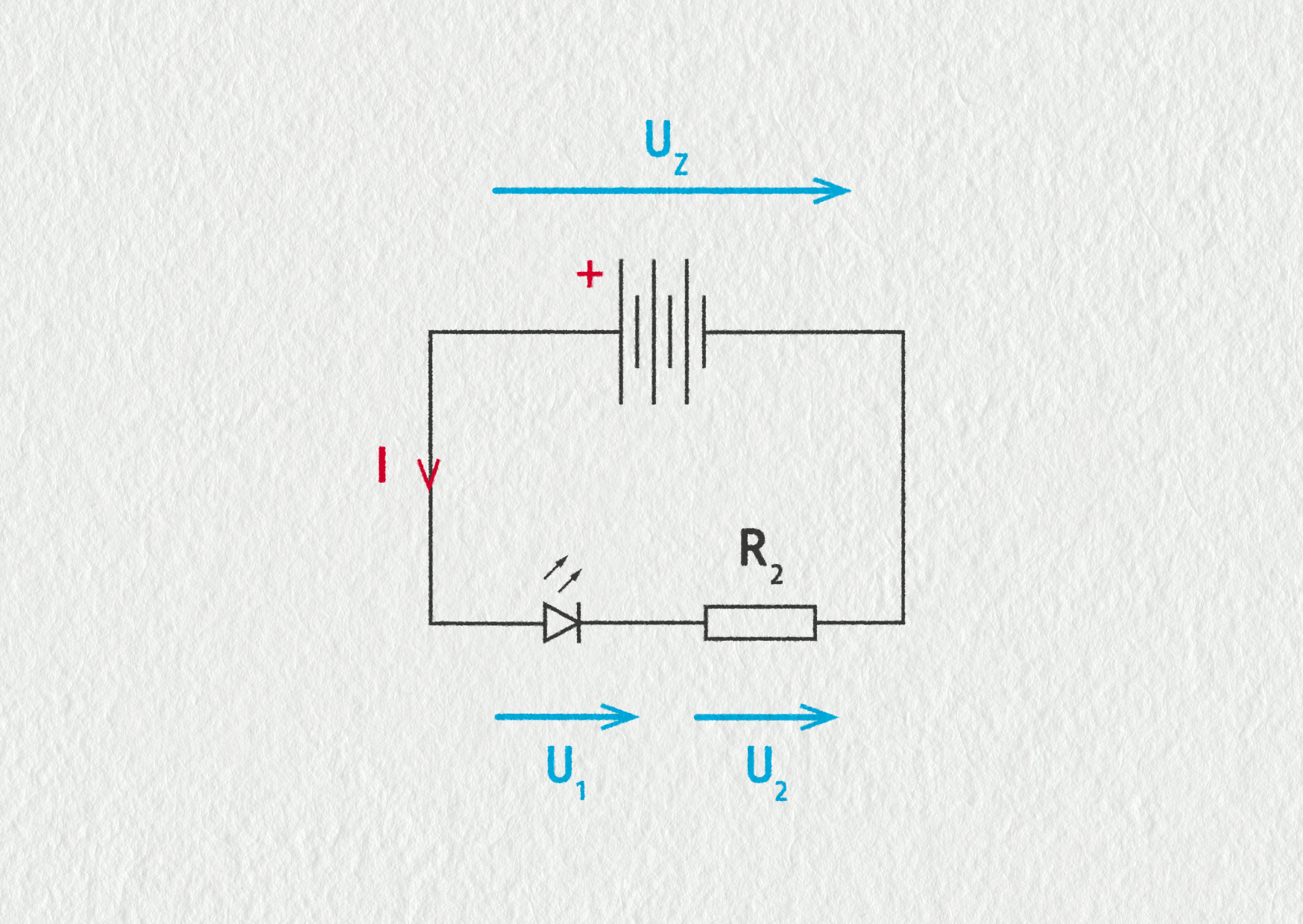
Zdroj

Zdroj
Víme, že \(U_\mathrm{Z}=6\ \mathrm{V}\), \(U_1=3{,}2\ \mathrm{V}\), takže napětí na rezistoru musí být \(U_1=2{,}8\ \mathrm{V}\) (vlastnost (2)). Diodou má téct proud \(I=10\ \mathrm{mA}\), stejný proud poteče i rezistorem (vlastnost (1)). Z Ohmova zákona vypočítáme odpor rezistoru \(R_1=U_1/I=280\ \mathrm{\Omega}\).
Dělič napětí
V sériovém obvodu se napětí zdroje \(U_\mathrm{Z}\) rozdělí na spotřebiče ve stejném poměru, jako je poměr jejich odporů. Napříkad při \(U_\mathrm{Z}=24\ \mathrm{V}\), \(R_1=20\ \mathrm{\Omega}\) a \(R_2=40\ \mathrm{\Omega}\) se napětí 24 V rozdělí v poměru 1:2, tj. 8 V a 16 V. Z daného napětí na zdroji \(U_\mathrm{Z}\) můžeme takto vyrobit libovolné (menší) výstupní napětí \(U_2\) k napájení jiných součástek.

Zdroj
Propočítáme hodnoty nezatíženého děliče – z kontaktů na \(R_2\) neodebíráme proud. Napětí na zdroji (vstupní) \(U_\mathrm{Z}=RI=(R_1 + R_2)I\), takže proud v obvodu \(I=U_\mathrm{Z}/(R_1+R_2)\). Výstupní napětí \(U_2=R_2I=R_2/(R_1+R_2)\cdot U_\mathrm{Z}\). Čili \(U_2\) je přímo úměrné vstupnímu napětí \(U_\mathrm{Z}\). Konstanta úměrnosti \(R_2/(R_1+R_2)\) se nazývá dělicí poměr.
Dělič napětí se dá elegantně využít i k měření neelektrických veličin – viz konstrukce teploměru.
Nevýhody sériového zapojení
Připojením další součástky do sériového obvodu se změní napětí na všech ostatních spotřebičích. Pokud se v některém místě sériový obvod přeruší, přestanou fungovat všechny spotřebiče. Domovní elektrospotřebiče se zapojují k síti paralelně.
Paralelní obvod
Uvažujme opět obvod tvořený zdrojem konstantního napětí \(U_\mathrm{Z}\) a dvěma rezistory o odporech \(R_1\) a \(R_2\) zapojenými tentokrát paralelně. Proudy v jednotlivých větvích a napětí na součástkách označíme podle obrázku.
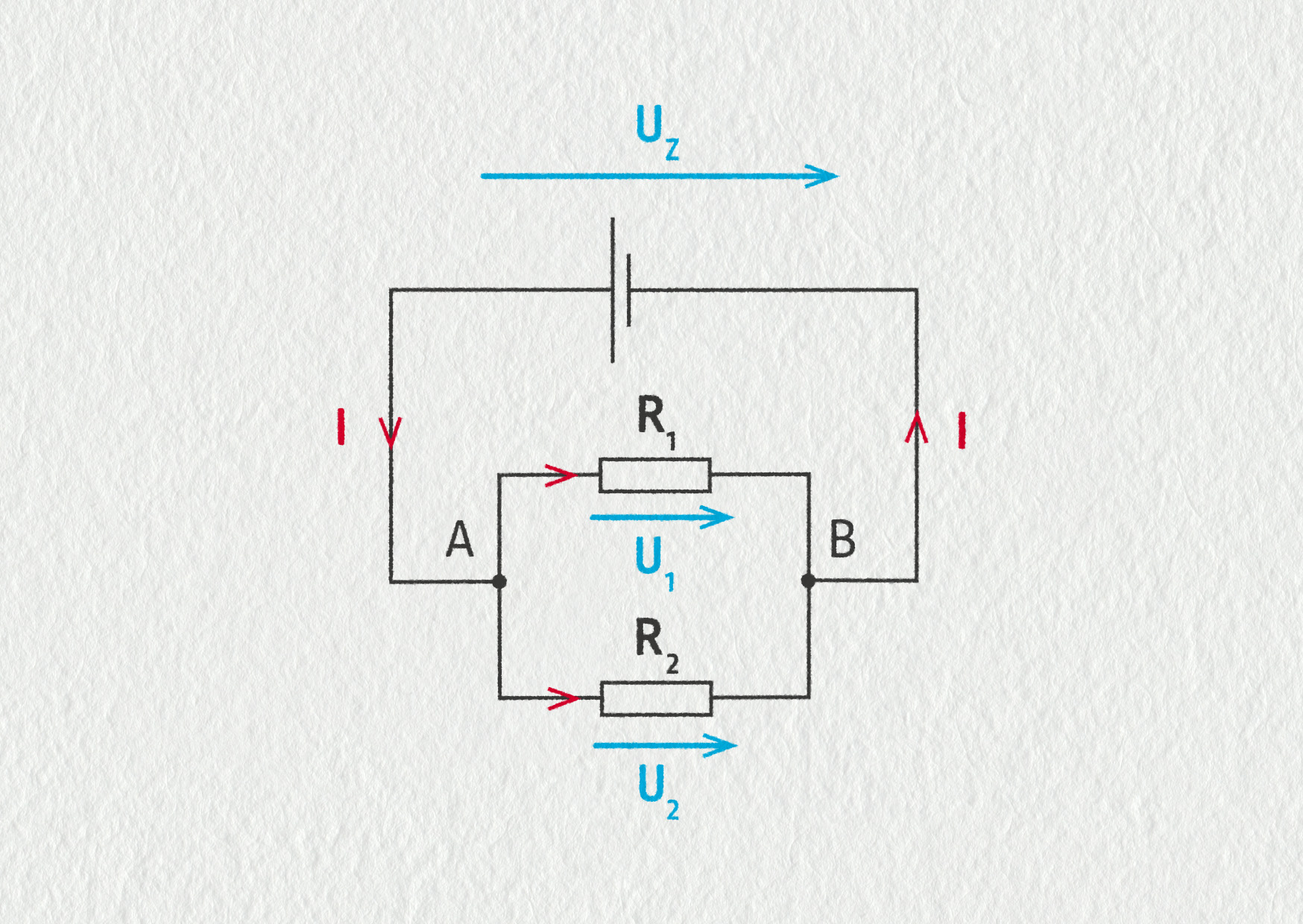
Zdroj
Vlastnosti elektrických veličin:
- Proud protékající zdrojem je součtem proudů v jednotlivých větvích, \(I = I_1 + I_2\).
- Na všech součástkách je stejné napětí, \(U_\mathrm{Z} = U_1 = U_2\).
- Pro celkový odpor \(R\) obvodu platí \(1/R = 1/R_1 + 1/R_2\).
- Čím větší odpor větve, tím menší proud. Proudy ve větvích jsou v opačném poměru než jejich odpory: \(I_1/I_2 = R_2/R_1\).
Odvození:
- Plyne ze zákona zachování náboje. V uzlu náboj nevzniká ani nezaniká, to, co za sekundu vteče dovnitř, musí za sekundu vytéct z uzlu ven, takže \(I = I_1 + I_2\).
- Plyne z definice napětí. Všimněte si, že všechny součástky jsou připojeny svými konci do stejných bodů A a B, takže \(U_{AB}=U_\mathrm{Z}\), ale též \(U_{AB}=U_1=U_2\).
- Z Ohmova zákona pro rezistory si vyjádříme proudy: \(I_1=U_1/R_1\), \(I_2=U_2/R_2\). Celkový odpor obvodu je \(R=U_\mathrm{Z}/I\), takže \(I=U_\mathrm{Z}/R\). Dosazením do (1) máme \(I = I_1 + I_2\), \(U_\mathrm{Z}/R = U_1/R_1 + U_2/R_2\). Napětí na všech součástkách jsou podle (2) stejná, \(U_{AB}=U_\mathrm{Z}=U_1=U_2\), takže \(U_{AB}/R=U_{AB}/R_1+U_{AB}/R_2\) a po vykrácení napětím \(U_{AB}\) získáváme vlastnost (3). Pokud by byl ve studovaném obvodu zapojen reálný zdroj s nenulovým vnitřním odporem, byl by celkový odpor obvodu součtem odporu spotřebičů a vnitřního odporu zdroje.
- Poněvadž \(U_1 = U_2\), máme po dosazení z Ohmova zákona \(R_1I_1=R_2I_2\), takže \(I_1/I_2 = R_2/R_1\).
Paralelní obvody se používají všude tam, kde spotřebiče musí být připojeny k témuž napětí a musí fungovat nezávisle na sobě – totiž připojení či odpojení některého z nich nesmí ovlivnit chod ostatních. Ukažme si to na dvou příkladech.
Domácí rozvodná síť
Téměř všechny domácí spotřebiče jsou konstruovány na střídavé napětí 230 V. Velmi zjednodušeně to znázorňuje následující ilustrační obrázek 8.28. Ve skutečnosti podobné fázové okruhy jsou tři a instalace obsahuje též spínací, jistící a ochranné prvky. Ve stavební dokumentaci se nejčastěji uvádí jen poloha jednotlivých elektronických prvků značkami danými normou, spojovací vodiče se nekreslí.
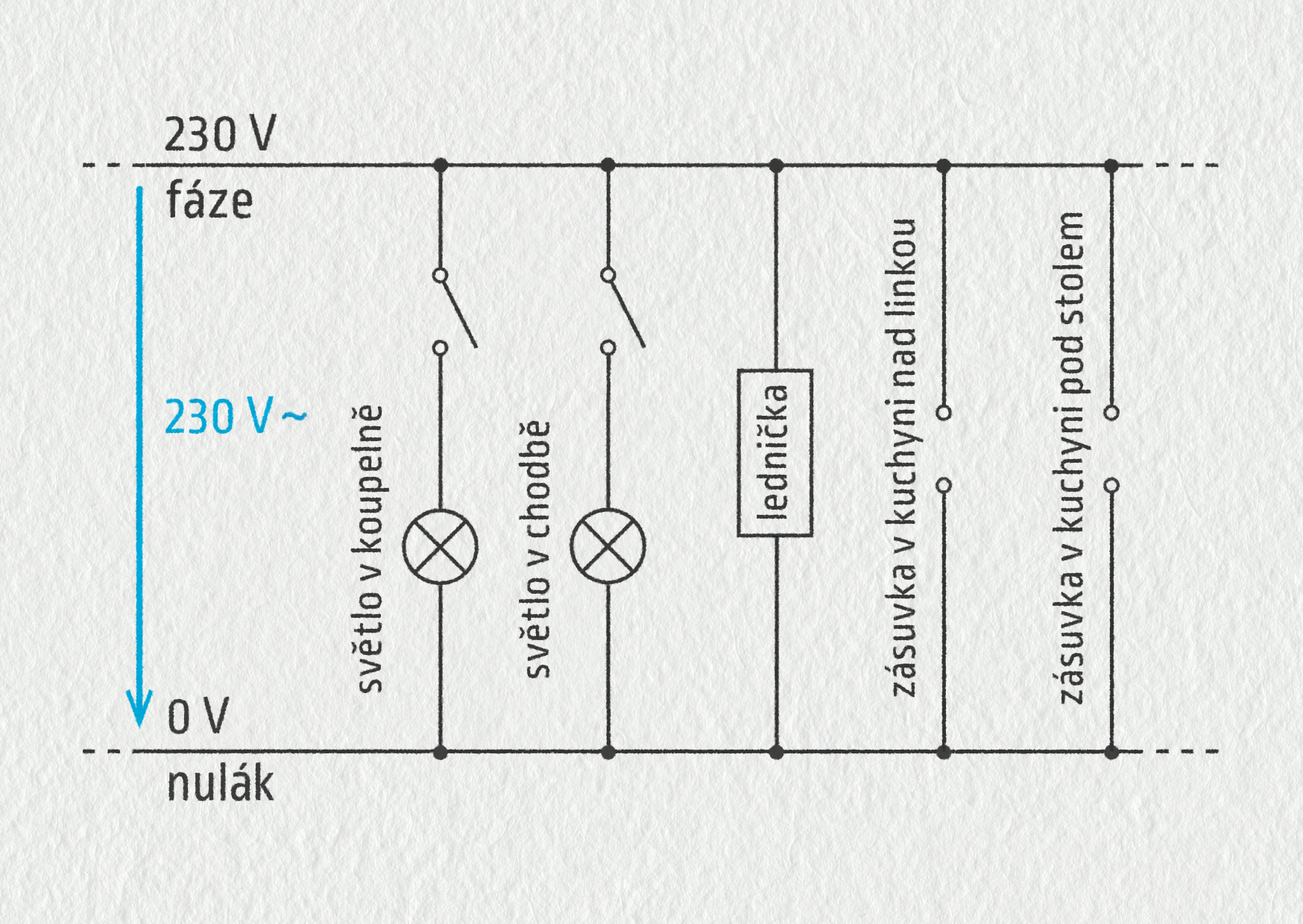
Zdroj
LED pásek
LED pásek skrytý pod kuchyňskou linkou nebo v obývací stěně dokáže vytvořit nečekanou světelnou pohodu. Jedná se o ohebný plošný spoj například o šířce řádově 1 cm a tloušťce řádově 1 mm osazený svítivými diodami. Skládá se například z pěticentimetrových segmentů, každý segment obsahuje v sérii tři LEDky a ochranný rezistor. Segmenty jsou k napájecímu stejnosměrnému napětí 12 V připojeny paralelně – viz galerie.
LED pásek

Zdroj
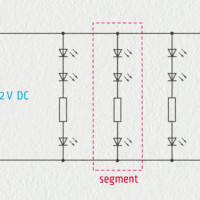
Zdroj

Zdroj

Zdroj
Reostat a potenciometr
Jedná se o jednu a tutéž součástku s nastavitelným odporem, která může být zapojena dvěma způsoby podle toho, jakou funkci má plnit.
Reostat a potenciometr

Zdroj

Zdroj

Zdroj
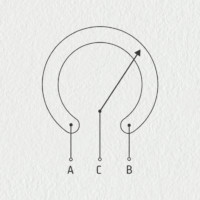
Konstrukčně je reostat velmi jednoduchý: odporový vodič je navinutý na izolačním válci a vyveden svorkami A a B. Tohoto vodiče se dotýká vodivý kontakt – tzv. jezdec – vyvedený na svorku C. Zatímco odpor vodiče \(R_{AB}\) mezi svorkami A a B je stálý, odpor mezi \(R_{AC}\), resp. \(R_{BC}\) lze měnit posunutím jezdce.
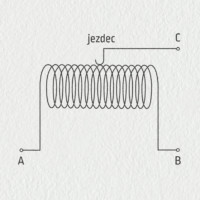
Zdroj

Zdroj
Zdroj

Zdroj
Reostat slouží jako mechanicky nastavitelný odpor (posuvem nebo otáčením vodivého kontaktu – jezdce). Používá se k regulaci proudu v obvodu, např. jako stmívač scénických světel v divadle nebo k regulaci hlasitosti sluchátek.
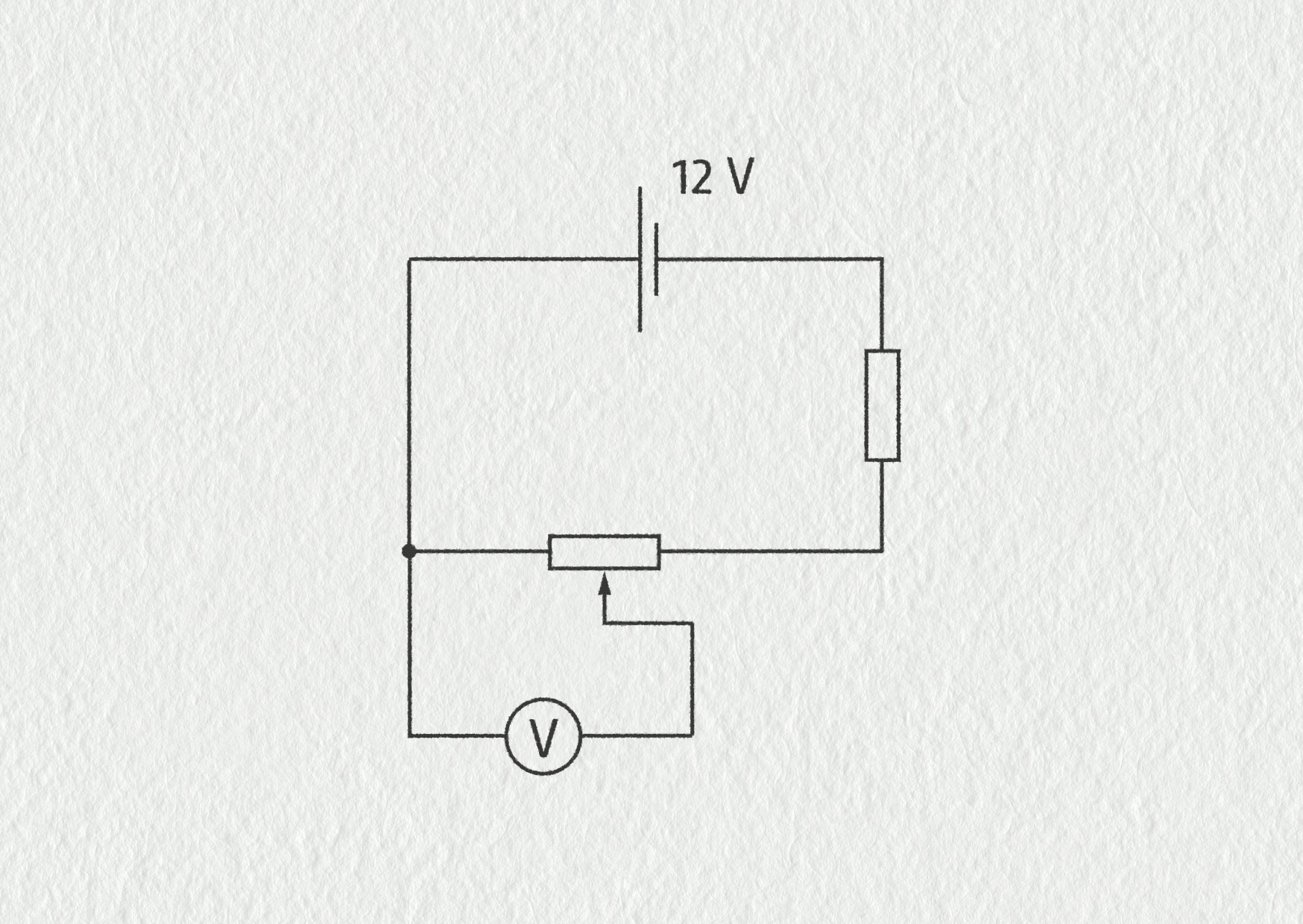
Potenciometr slouží jako dělič napětí, přičemž jezdcem nastavujeme poměr mezi \(R_1\) a \(R_2\). Využívá se k regulaci napětí a k mechanickému ovládání elektrických zařízení a obvodů, např. jako ovladač hlasitosti u reproduktorů.

Zdroj
Zdroj
Jaké napětí ve voltech ukáže voltmetr, když bude jezdec
Proud a napětí se dají regulovat i pomocí polovodičové elektroniky, která je vhodná zejména ke stabilizaci těchto veličin.
Odpor ampérmetru a voltmetru
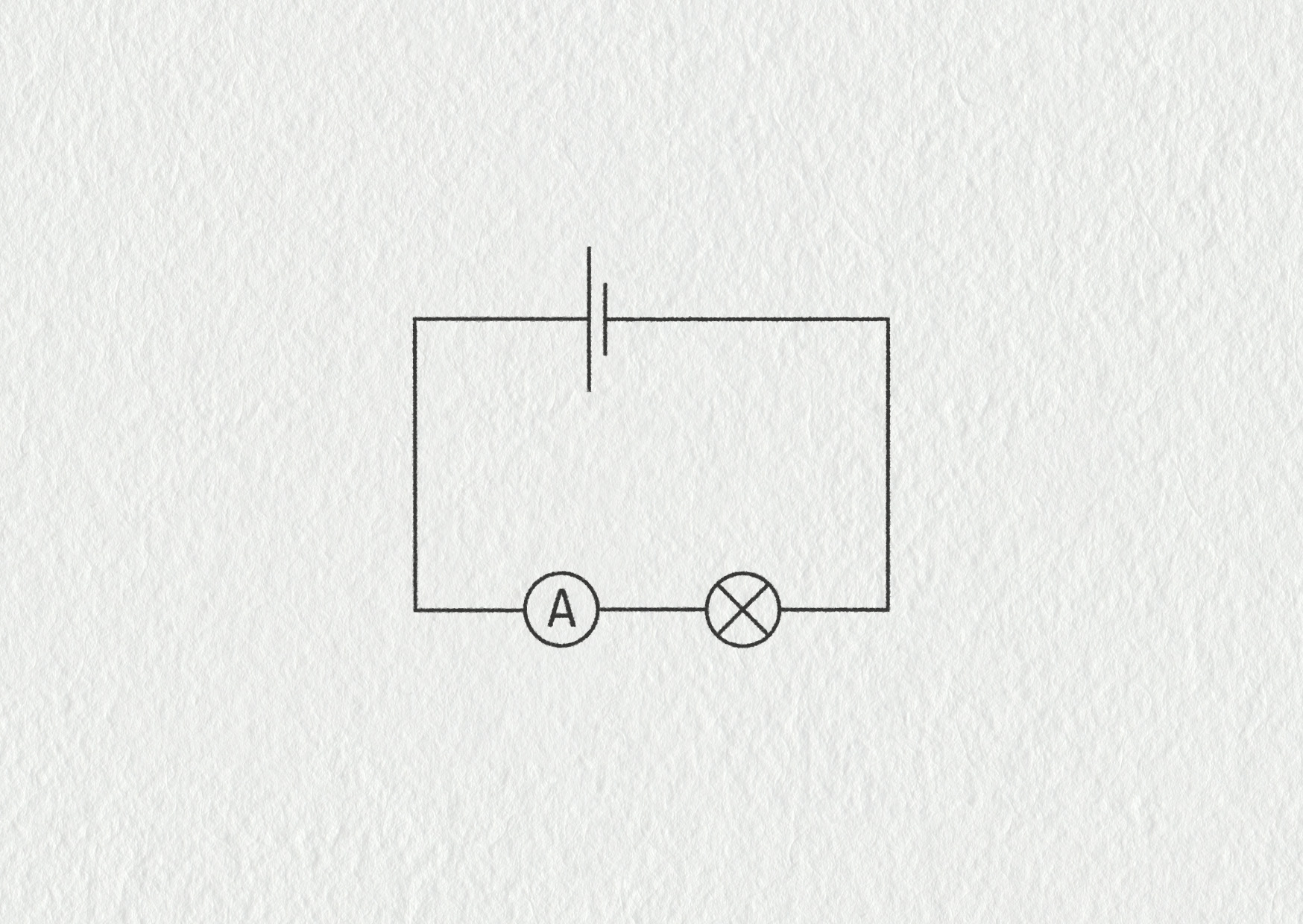
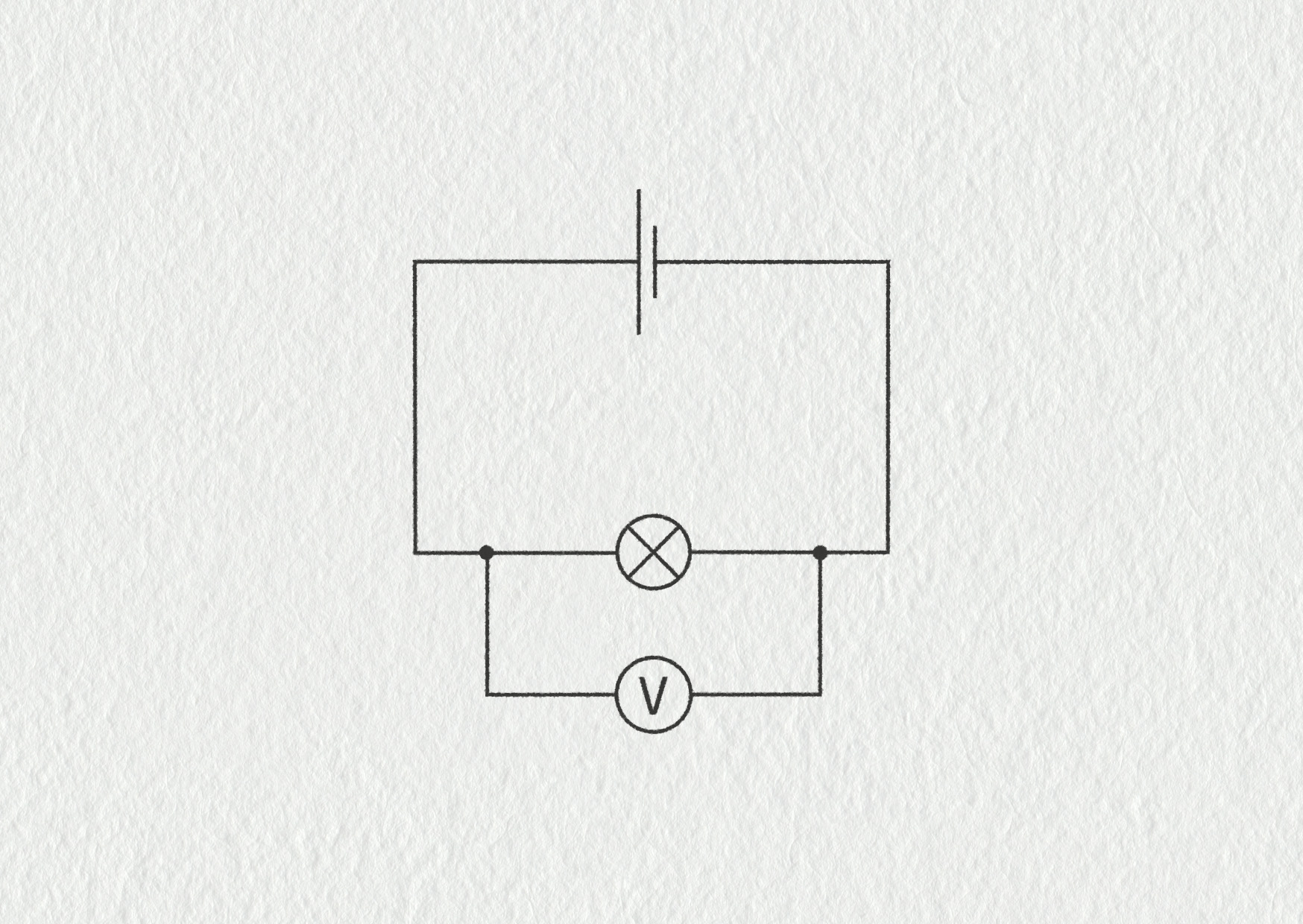
Ampérmetry se konstruují tak, aby svou přítomností (svým odporem) neovlivnily měřenou hodnotu proudu. Ampérmetr se zapojuje sériově a jeho vnitřní odpor musí být co nejmenší (řádově 10−1 Ω). Naopak voltmetr měřící napětí mezi body A a B musí mít vnitřní odpor co největší (řádově desítky MΩ), aby jeho přítomností nevznikla nová vodivá větev mezi A a B.
Zdroj
Zdroj

