Spektroskopie
Cvičení 1
Vysvětlete rozdíl mezi čárovým a spojitým spektrem. Vyjmenujte pro každé z nich několik různých zdrojů záření, pro které je charakteristický tento druh spektra.
Cvičení 2
Jak vzniká absorpční spektrum? Nakreslete jednoduché schéma přístroje, který toto spektrum umožní pozorovat.
Cvičení 3
Rtuťová výbojka vysílá polychromatické světlo. Následující diagram znázorňuje několik energetických hladin atomu rtuti.
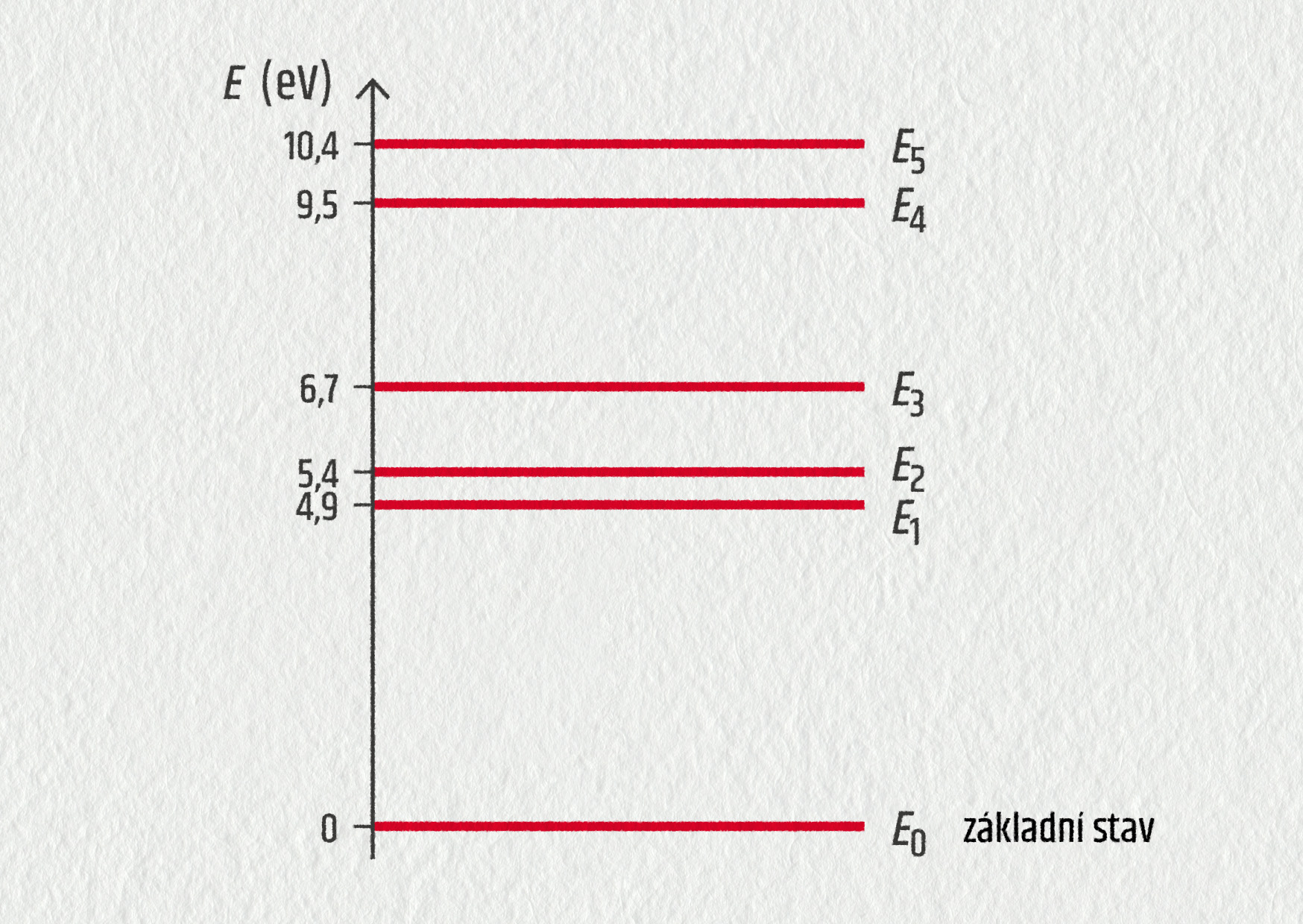
Zdroj
Co znamená výraz „polychromatické světlo“?
Zjednodušený energetický diagram ukazuje, že energie atomu rtuti nemůže nabývat libovolných hodnot. To znamená, že energie je
- absorbována;
- kvantována;
- spojitá?
Emise záření
Jedna z viditelných čar vysílaných rtuťovou výbojkou odpovídá elektronovému přechodu mezi hladinami \(E_4\) a \(E_3\).
- Určete vztah mezi změnou energie \(\Delta E\) a vlnovou délkou \(\lambda_{43}\) vyslaného záření. Vypočítejte hodnotu této vlnové délky a určete barvu světla (viz obrázek).
- Určete nejkratší vlnovou délku, kterou může atom rtuti vyslat, jestliže se nachází v energetickém stavu E4. Do jaké spektrální oblasti (UV, viditelná, IR) tato čára patří? Vysvětlete.
- Určete všechny vlnové délky, které leží ve viditelném oboru. Jakým přechodům elektronů odpovídají? Výsledek porovnejte s viditelným spektrem (viz obrázek).

Zdroj
Absorpce záření
- Nyní mějme atom rtuti v základním stavu určeném energií \(E_0\). Je na něj vyslán foton s energií \(E_\mathrm{fot}=1{,}0\ \mathrm{eV}\). Může být tento foton pohlcen? Vysvětlete.
- Nyní na atom rtuti v základním stavu dopadá foton s energií \(E_\mathrm{fot}=4{,}9\ \mathrm{eV}\) Jaká může být interakce atomu rtuti s fotonem? Vysvětlete.
- Určete energie fotonů, které mohou být absorbovány, jestliže se atom rtuti nachází v základním stavu.
- Polychromatické světlo znamená mnohobarevné;
- kvantována;
Emise záření:
- \(E_4-E_3=hc/\lambda_{43}\), \(\lambda_{43}=443\ \mathrm{nm}\), fialová barva;
- 131 nm, ultrafialová oblast;
- 690 nm; přechod z E3 do E1:
Absorpce záření:
- nemůže, energie neodpovídá žádnému rozdílu energie hladin a energie E0;
- může být pohlcen, atom bude excitován na \(E_1\);
- 4,9 eV, 5,40 eV, 6,7 eV, 9,5 eV a 10,4 eV
Cvičení 4
V helium–neonovém laseru je energie získaná vybuzenými ionty He+ předána iontům Ne+, které se pak nacházejí ve stavech s vysokou energií, odkud dochází k několika různým elektronovým přeskokům.
Předpokládejme (pro zjednodušení), že nulová hodnota energie je zde určena, jestliže se iont Ne+ nachází ve svém základním stavu.
Zde máme velmi zjednodušený diagram znázorňující základní excitované stavy iontu Ne+.
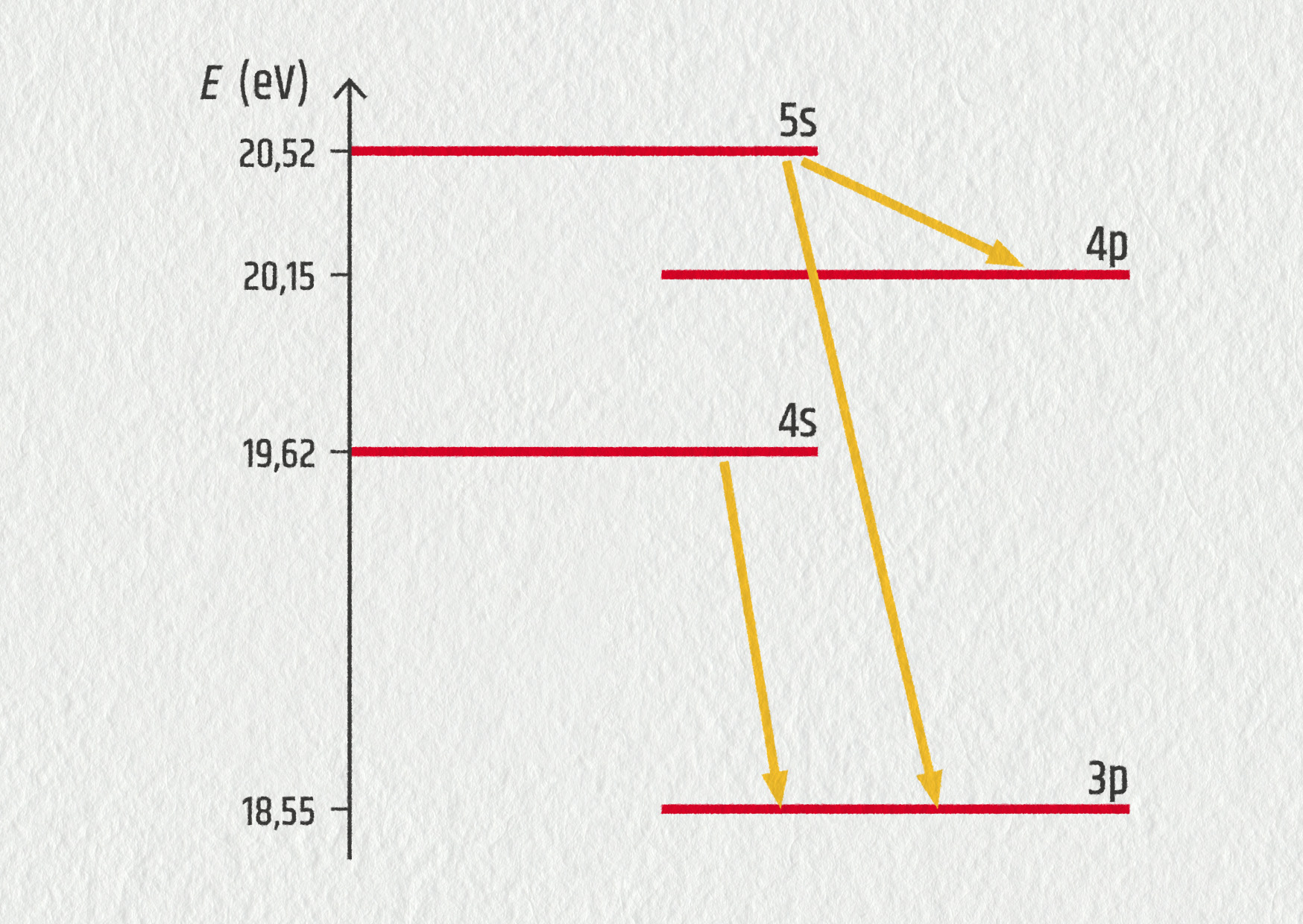
Zdroj
- Který ze znázorněných přechodů leží ve viditelné oblasti?
- Vypočítejte vlnovou délku tohoto přechodu.
- Jaká barva je pro helium–neonový laser typická? Odpovídá to vašemu výpočtu?
- přechod 5s → 3p, jehož energie je 1,97 eV, což leží ve viditelné oblasti spektra;
- 630 nm;
- červená barva, odpovídá to výpočtu
Cvičení 5
Jestliže ve výbojové trubici excitujeme páry sodíku, trubice vydává jasné žlutooranžové světlo. Kvalitním spektrometrem s dobrou rozlišovací schopností můžeme určit vlnové délky tohoto sodíkového dubletu: \(\lambda_1=589{,}59\ \mathrm{nm}\), \(\lambda_2=588{,}99\ \mathrm{nm}\).
Tyto vlnové délky odpovídají dvěma velmi blízkým excitovaným stavům označovaným 3p a základnímu stavu označovanému 3s. Základnímu stavu přiřazujeme energii 0 eV.
- Určete energie, které odpovídají zmíněným excitovaným stavům označeným 3p. Výsledek vyjádřete v J a v eV.
- Můžeme říci, jaké vlnové délky by byly absorbovány, jestliže osvětlíme páry sodíku bílým světlem se spojitým spektrem?
- Abychom vytvořili iont sodíku Na+ z neutrálního atomu, musíme mu dodat energii 5,14 eV. Jaká je vlnová délka záření, které by – při interakci s atomem sodíku – vznik iontu umožnilo? Do jaké oblasti spektra toto záření spadá?
- Jestliže má záření vlnovou délku 200 nm, s jakou rychlostí bude z atomu sodíku uvolněn elektron?

Zdroj
- \(3{,}374\cdot10^{-19}\ \mathrm{J} = 2{,}11\ \mathrm{eV}\) a \(3{,}377\cdot10^{-19}\ \mathrm{J} = 2{,}108\ \mathrm{eV}\);
- ano, budou absorbovány právě tyto dvě vlnové délky;
- 242 nm, ultrafialové záření;
- \(6{,}1\cdot10^{5}\ \mathrm{m/s}\)
Cvičení 6
Určete vlnovou délku odpovídající hraně v Balmerově sérii. Tato série se shoduje s přechody do prvního excitovaného stavu atomu vodíku. Hranou rozumíme největší možnou energii přeskoku.
Cvičení 7
Určete hranu Lymanovy série, tj. vlnovou délku odpovídající největší energii při přechodu atomu vodíku do základního stavu.
Cvičení 8
Jaká je velikost hybnosti fotonu vyzářeného při přechodu atomu vodíku ze stavu s \(n_1=6\) do stavu s \(n_2=1\)? Energie atomu vodíku v základním stavu je \(E_0=-13{,}6\ \mathrm{eV}\).
Cvičení 9
Trochu historie:
Studium světla, záření horkých těles nebo záření výbojových trubic bylo ve druhé polovině 19. století velmi oblíbené. V roce 1885 švýcarský fyzik Johann Balmer prokázal čtyři viditelné čáry spektra vodíku. Poté následovaly další objevy: Lyman (UV), Paschen (IR), Brackett (IR) a Pfund (IR).
Balmerova práce a po něm práce švédského fyzika Johanna Rydberga umožnily dokázat, že vlnové délky lze vypočítat pomocí jednoduchého vztahu zahrnujícího celá čísla n a p:
\[ \frac1{\lambda_{np}} = R_\mathrm{H}\left(\frac1{p^2}-\frac1{n^2}\right)\;. \]Avšak jednalo se pouze o empirický vztah zjištěný na základě měření emitovaných vlnových délek. Proč ale tento vztah nebyl dokázán? To byla záhada.
Její objasnění přinesl až v roce 1913 Niels Bohr se svojí kvantifikací energií atomů a teorií atomu vodíku. Sklidil za ni velký úspěch a v roce 1922 byl odměněn Nobelovou cenou za fyziku.
(Upřesněme, že abychom mohli vysvětlit jemnou strukturu spektra vodíku, musíme pracovat s eliptickými trajektoriemi elektronů a začít používat soubor 4 kvantových čísel.)
Otázky:
- Jestliže se elektron nachází na hladině řádu \(n\), energie atomu vodíku je určena vztahem \(E_n=-E_0/n^2\), kde \(E_0=13{,}6\ \mathrm{eV}\). Vypočítejte energie jednotlivých energetických stavů atomu vodíku. Znázorněte je v měřítku 1 cm pro 1 eV do energetického diagramu.
- Odvoďte vztah pro \(1/\lambda_{np}\). Vypočítejte hodnotu Rydbergovy konstanty \(R_\mathrm{H}\).
- Vypočítejte vlnové délky všech čar ve viditelné oblasti spektra vodíku. Odpovídají vaše výsledky vlnovým délkám znázorněným na obrázku?
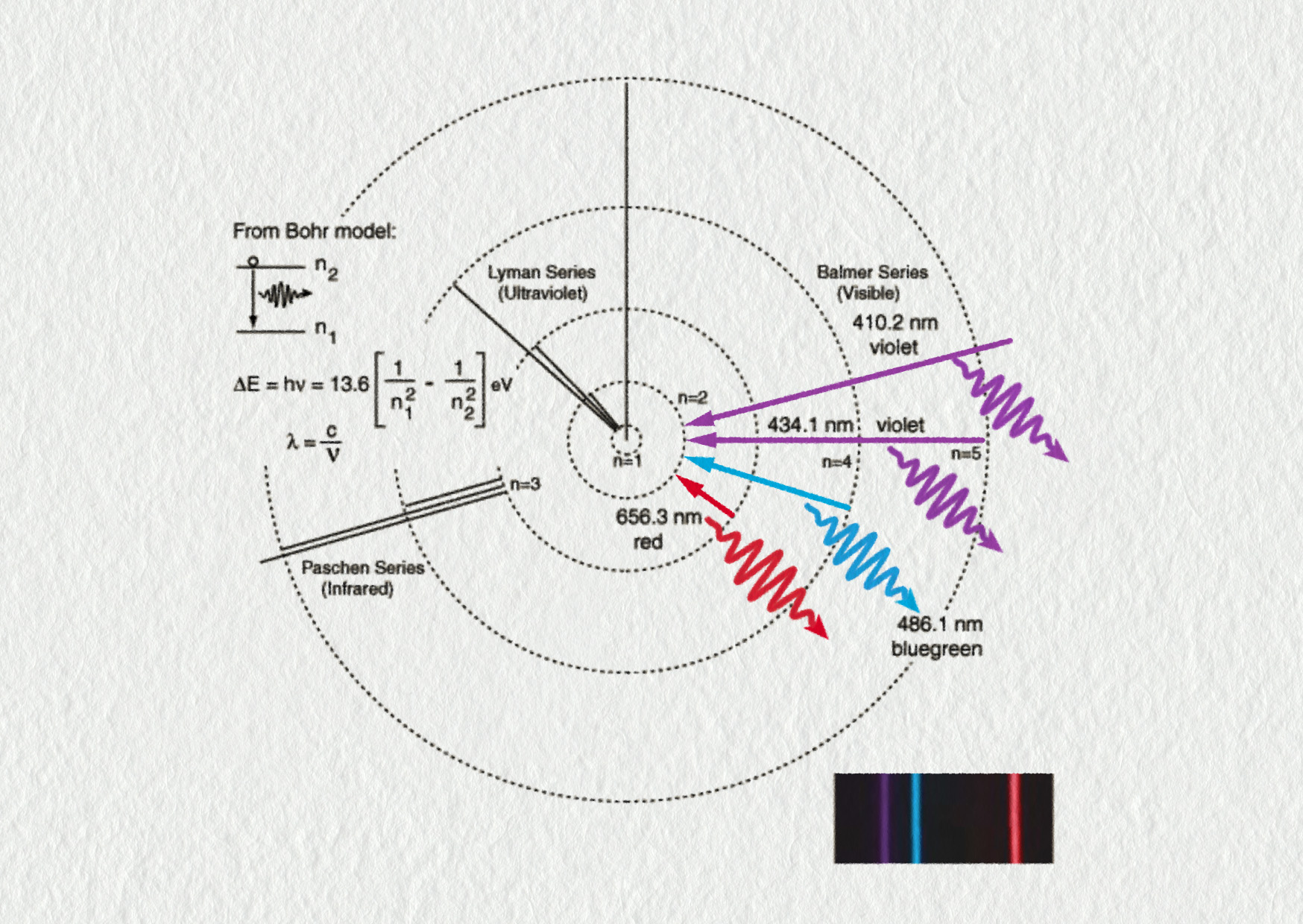
Zdroj
-
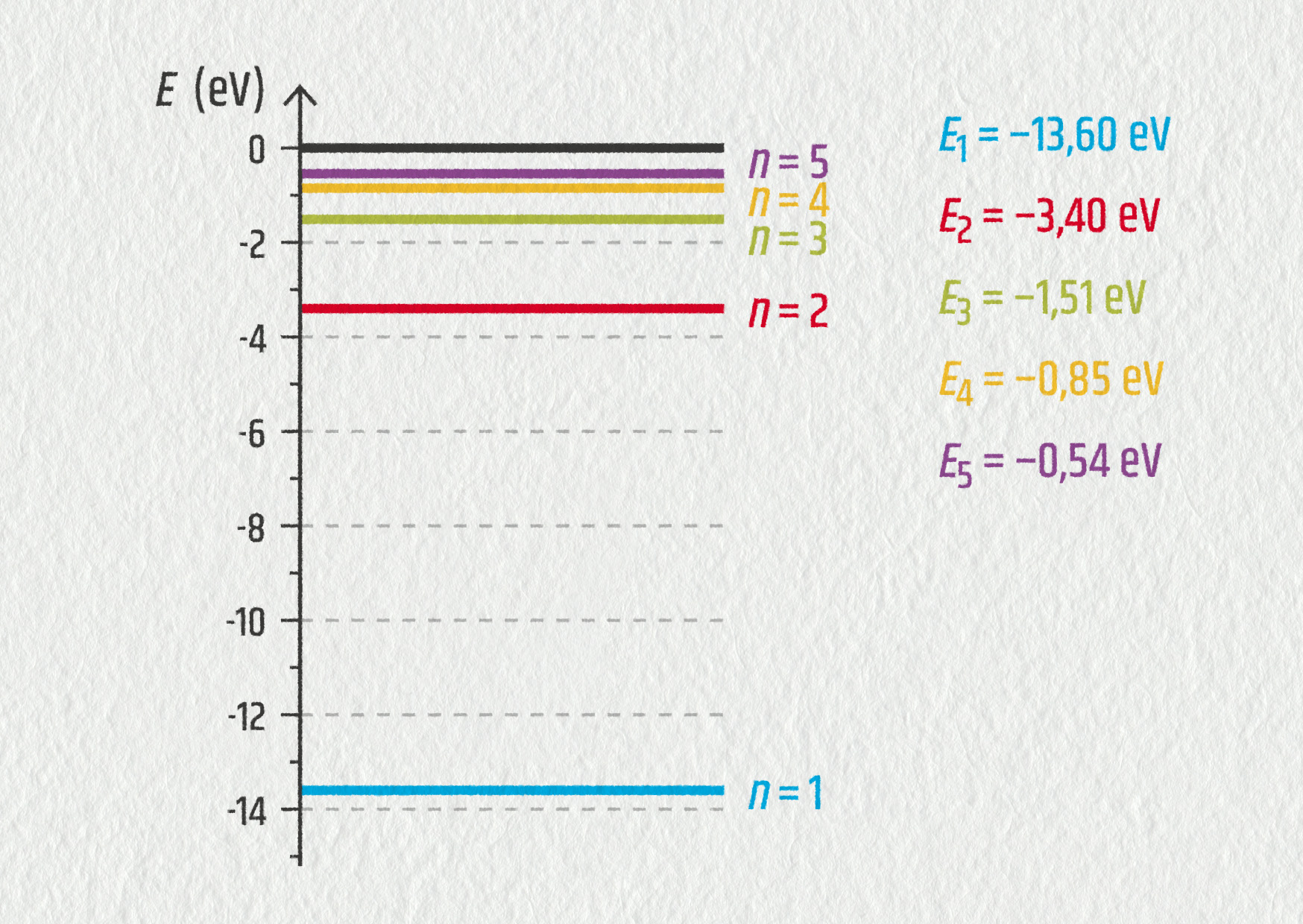
25.42 – řešení;
Zdroj - \(\displaystyle\frac1{\lambda_{np}} = \frac{E_0}{hc}\left(\frac1{p^2}-\frac1{n^2}\right)\), \(R_\mathrm{H}=E_0/(hc)=1{,}10\cdot10^7\ \mathrm{m}^{-1}\);
- \(\lambda_{32}=656{,}9\ \mathrm{nm}\), \(\lambda_{42}=486{,}5\ \mathrm{nm}\); \(\lambda_{52}=434{,}5\ \mathrm{nm}\); \(\lambda_{62}=410{,}6\ \mathrm{nm}\), ano, odpovídají

