Fotoelektrický jev

Pokud svazek světla narazí na překážku, může být každý jednotlivý foton buď pohlcen, odražen nebo rozptýlen. Jestliže je odražen, nedochází k výměně energie. Je-li naopak pohlcen, zaniká a kvantum energie o velikosti \(hf\) je předáno materiálu. Při rozptylu se sice energie fotonu zmenší, je to ale tím, že foton zanikne a vznikne foton s menší energií.

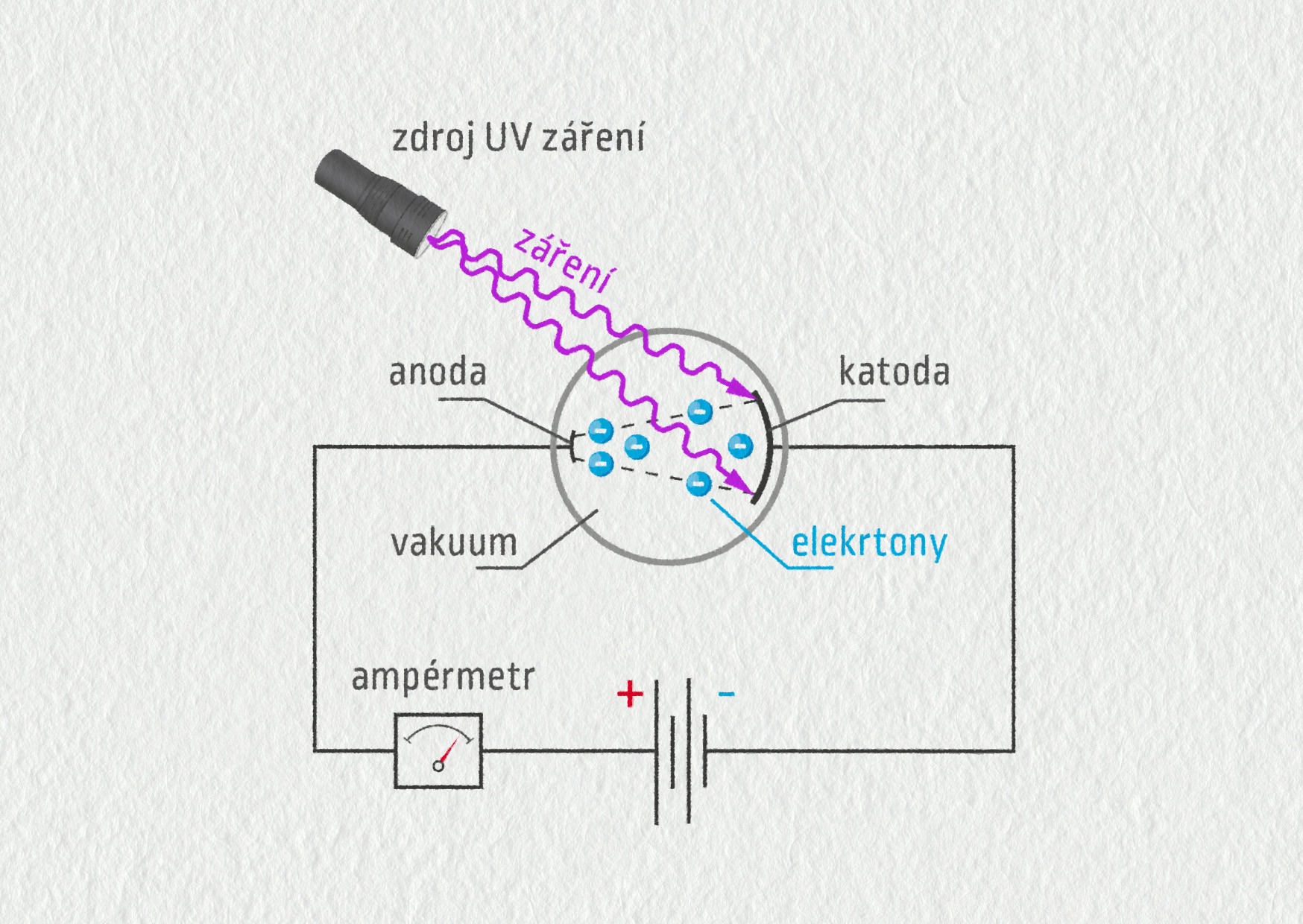
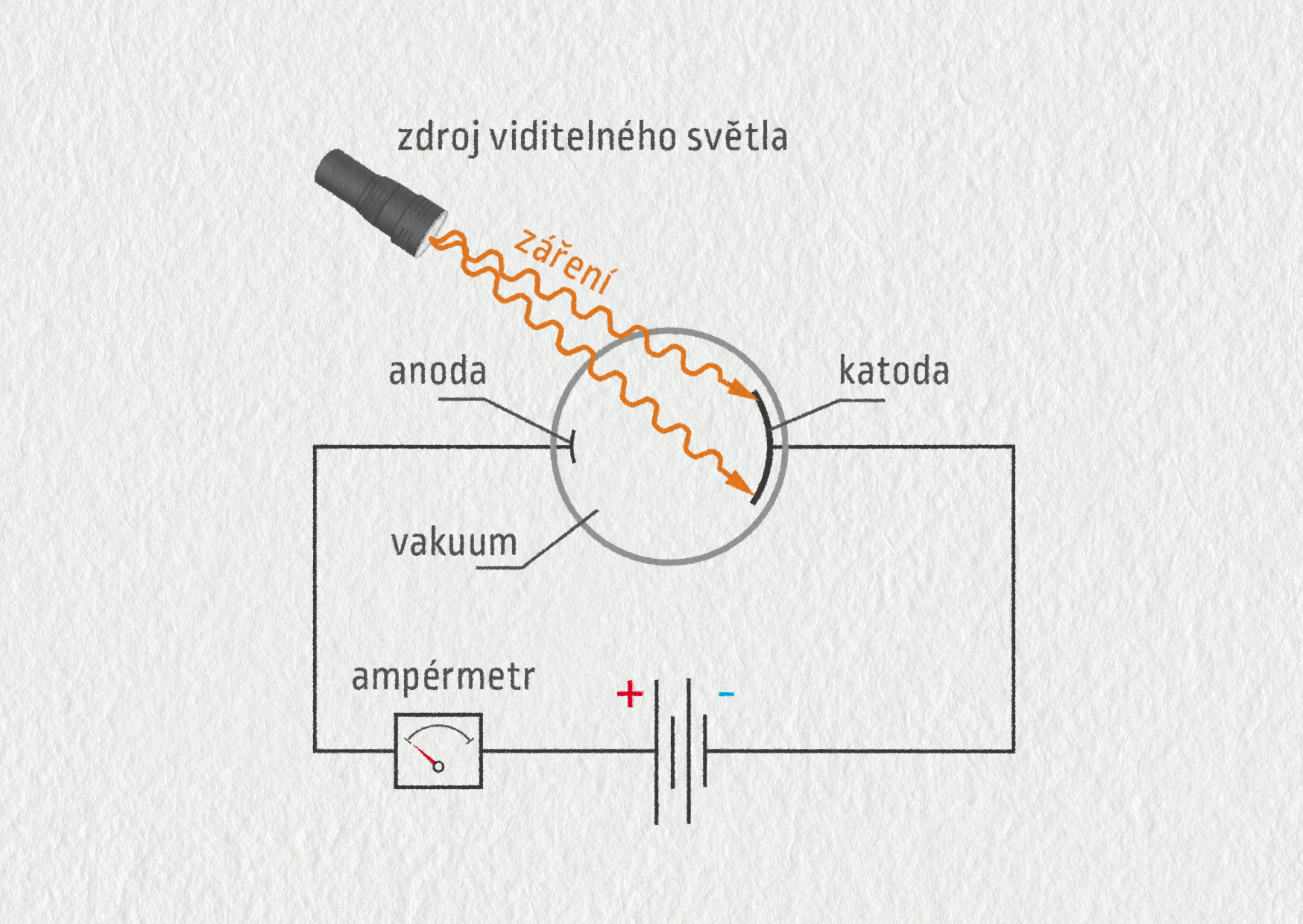
V roce 1888 objevil německý fyzik Heinrich Hertz zajímavý jev. Při dopadu světla (záření) na povrch materiálu (nejčastěji kovu) z něj mohou být uvolněny elektrony. K jejich uvolnění však dochází pouze od určité prahové frekvence, která je charakteristická pro daný kov. Ozáříme-li kov světlem s nižší frekvencí, uvolnění elektronů nenastane. Nepomůže ani zvětšení intenzity světla.

Výsledek experimentu byl v rozporu s tehdejšími představami o světle. Podle vlnové teorie by světelné záření mělo rozkmitávat částice v látce bez ohledu na frekvenci dopadajícího záření a při zvýšení intenzity světla by mělo být uvolňováno více elektronů.

Vysvětlení nabídl roku 1905 Albert Einstein. Je nutné předpokládat, že se záření chová jako proud částic. Každý z fotonů nese energii \(E=hf\). Jestliže je tato energie dostatečná, je z materiálu uvolněn elektron s určitou rychlostí \(v\) a foton je pohlcen. Aby k tomu došlo, musí být energie nesená fotonem alespoň rovna energii, kterou musíme elektronu dodat, abychom ho z látky uvolnili – tzv. výstupní práci \(W_0\). Tato energie závisí na daném materiálu.

Jaké možnosti tedy nastávají?

Energie nesená fotonem \(hf\) je příliš malá (\(hf<W_0\)). V tomto případě fotoelektrický jev nenastává. Záření není schopno z materiálu uvolnit elektrony při libovolně vysoké intenzitě světla.
Energie nesená fotonem \(hf\) je přesně tak velká (\(hf=W_0\)), aby fotoelektrický jev nastal. Foton je pohlcen materiálem a jeho energie je použita k uvolnění elektronu z materiálu. Žádná další energie již nezbývá, uvolněn je tedy elektron s nulovou rychlostí.
Energie nesená fotonem \(hf\) je velká (\(hf>W_0\)), dochází k fotoelektrickému jevu. Část energie fotonu je spotřebována na uvolnění elektronu (výstupní práce \(W_0\)), přesto však ještě zbývá nějaká část energie, kterou odnáší uvolněný elektron ve formě své kinetické energie.

Vše výborně shrnuje jedna rovnice – celková energetická bilance, kterou nazýváme Einsteinova rovnice pro fotoefekt (jiné označení pro fotoelektrický jev):

\[ hf = W_0 + E_\mathrm{k}\; \]

Kromě energie fotonu \(hf\) a výstupní práce elektronu v daném materiálu \(W_0\) zde také vystupuje kinetická energie uvolněného fotonu \(E_\mathrm{k}=\frac12mv^2\), kde \(m\) je hmotnost elektronu a \(v\) jeho rychlost.

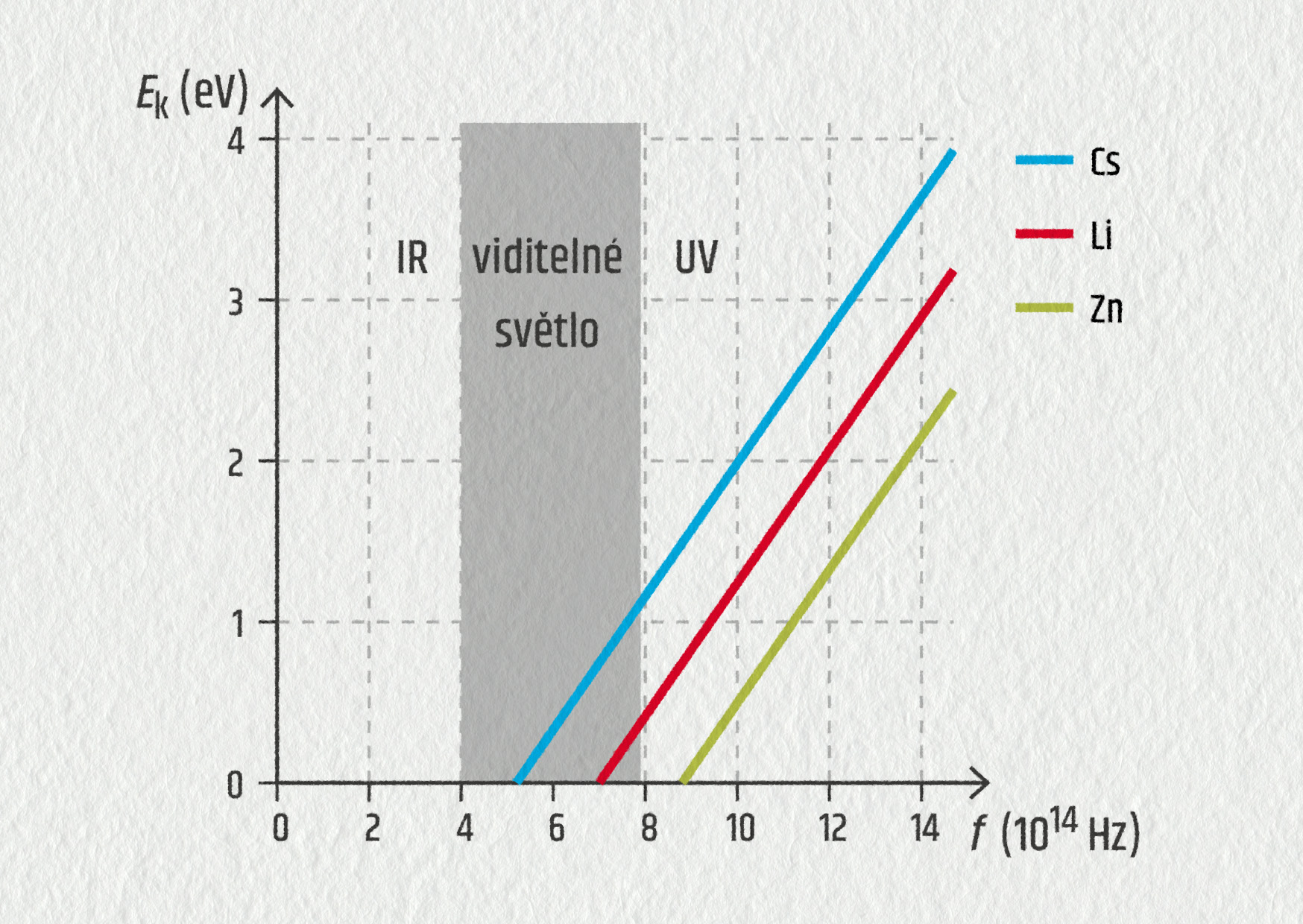
Následující graf ukazuje závislost kinetické energie uvolněných elektronů na frekvenci dopadajícího záření pro tři různé prvky. Můžeme na něm zřetelně vidět, kdy fotoelektrický jev nastane, a kdy ne:

25.12 – Závislost kinetické energie uvolněného elektronu na frekvenci dopadajícího záření.
Zdroj

Vezměme například lithium Li. Fotoelektrický jev nastává až při frekvenci dopadajícího záření kolem 7,0 ⋅ 10¹⁴ Hz, dojde k němu tedy pouze tehdy, osvítíme-li lithium fialovým světlem. Ovšem pro cesium najdeme tuto hranici již v oblasti oranžového světla při frekvenci 5,2 ⋅ 10¹⁴ Hz. Oproti tomu zinek má hranici pro fotoefekt až v oblasti ultrafialového světla. Jeho mezní frekvence je 8,8 ⋅ 10¹⁴ Hz. U zinku tedy fotoelektrický jev nevyvoláme viditelným zářením!

Příklad 1

Jeden typ elektronky používá jako katodu sodík. Pro sodík nastává fotoelektrický jev při vlnové délce světla nejvýše 526 nm.

Jaká je výstupní práce elektronu pro sodík? (Výsledek vyjádřete v eV.)
Nastane fotoelektrický jev, jestliže na sodíkovou katodu dopadá ultrafialové světlo o vlnové délce 348 nm? Pokud ano, jakou kinetickou energii v eV budou mít uvolněné elektrony?

Řešení:

a) Výstupní práce pro daný prvek je rovna součinu Planckovy konstanty \(h\) a prahové frekvence \(f_0\), od které fotoefekt nastává. Pro výstupní práci tak dostáváme

\[ W_0 = hf_0 = \frac{hc}{\lambda_0} = \frac{6{,}63\cdot10^{-34}\cdot3\cdot10^8}{526\cdot10^{-9}}\ \mathrm{J} = 3{,}78\cdot10^{-19}\ \mathrm{J} = 2{,}36\ \mathrm{eV} \]

b) Jestliže na katodu dopadá ultrafialové světlo o vlnové délce 348 nm, fotoefekt nastane, protože vlnová délka je menší než mezní vlnová délka. Frekvence dopadajícího světla tedy musí být větší než mezní frekvence \(f_0\). Kinetickou energii uvolněného elektronu vyjádříme z rovnice fotoefektu vztahem

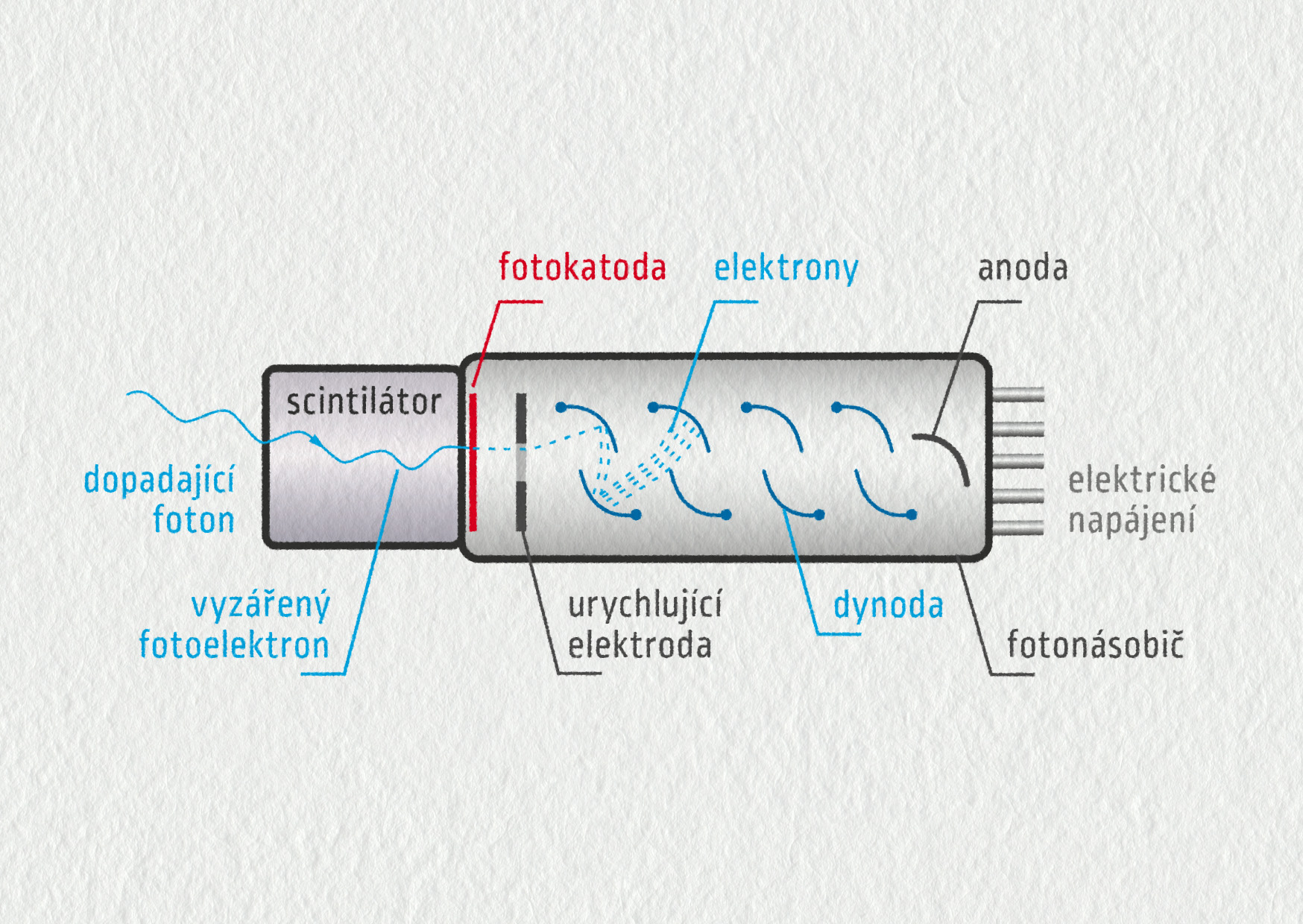
\[ E_\mathrm{k} = \frac{hc}{\lambda} - W_0 = \] \[ = hc\left(\frac1{\lambda}-\frac1{\lambda_0}\right) = \] \[ = 6{,}63\cdot10^{-34}\cdot3\cdot10^8\cdot\left(\frac1{348\cdot10^{-9}}-\frac1{526\cdot10^{-9}}\right) = \] \[ = 1{,}93\cdot10^{-19}\ \mathrm{J} = \] \[ = 1{,}20\ \mathrm{eV}\;. \]

Zatím jsme se zabývali pouze situací, kdy dopadající záření uvolní elektrony tak, že opouštějí daný materiál. V tomto případě hovoříme o vnějším fotoelektrickém jevu. Vnějšího fotoelektrického jevu využíváme ve fotonásobičích, což jsou tak citlivá elektronická zařízení, že umožňují detekci i jediného fotonu.

25.13 – Schéma fotonásobiče. Foton dopadající na katodu elektronky generuje elektron, který je následně mnohonásobně zesílen. Získáme tak měřitelný elektrický signál.
Zdroj

Zcela běžná je však také situace, kdy uvolněné elektrony zůstávají v daném materiálu, nejčastěji v polovodiči. Tento jev nazýváme vnitřní fotoelektrický jev a využíváme ho ve fotodiodě nebo fotorezistoru, fotovoltaickém článku, fotovoltaickém panelu nebo také na čipech CCD našich telefonů a digitálních kamer.

Využití fotoelektrického jevu

25.14d – Fotovoltaické panely na střeše domu.
Zdroj

Comptonův jev

Patrně nejdůležitějším objevem, který potvrdil částicovou povahu světla a ukončil pochybnosti fyziků o povaze světla, byl Comptonův jev. Roku 1923 Arthur Holly Compton studoval interakci záření a volných elektronů. Při svém experimentu ozařoval rentgenovými paprsky uhlíkový terč. Při tom měřil vlnovou délku fotonů pro daný rozptylový úhel. Podle vlnové teorie bychom měli získat klasický difrakční obrazec. Vlnová délka dopadajícího i rozptýleného záření jsou v takovém případě stejné.

Výsledek experimentu však ukazuje něco jiného. Některé fotony nejsou vůbec rozptýleny a nemění se ani jejich frekvence, zatímco jiné fotony jsou rozptýleny pod různými úhly a jejich vlnová délka je větší než vlnová délka záření dopadajícího na elektrony, mají tedy menší energii.

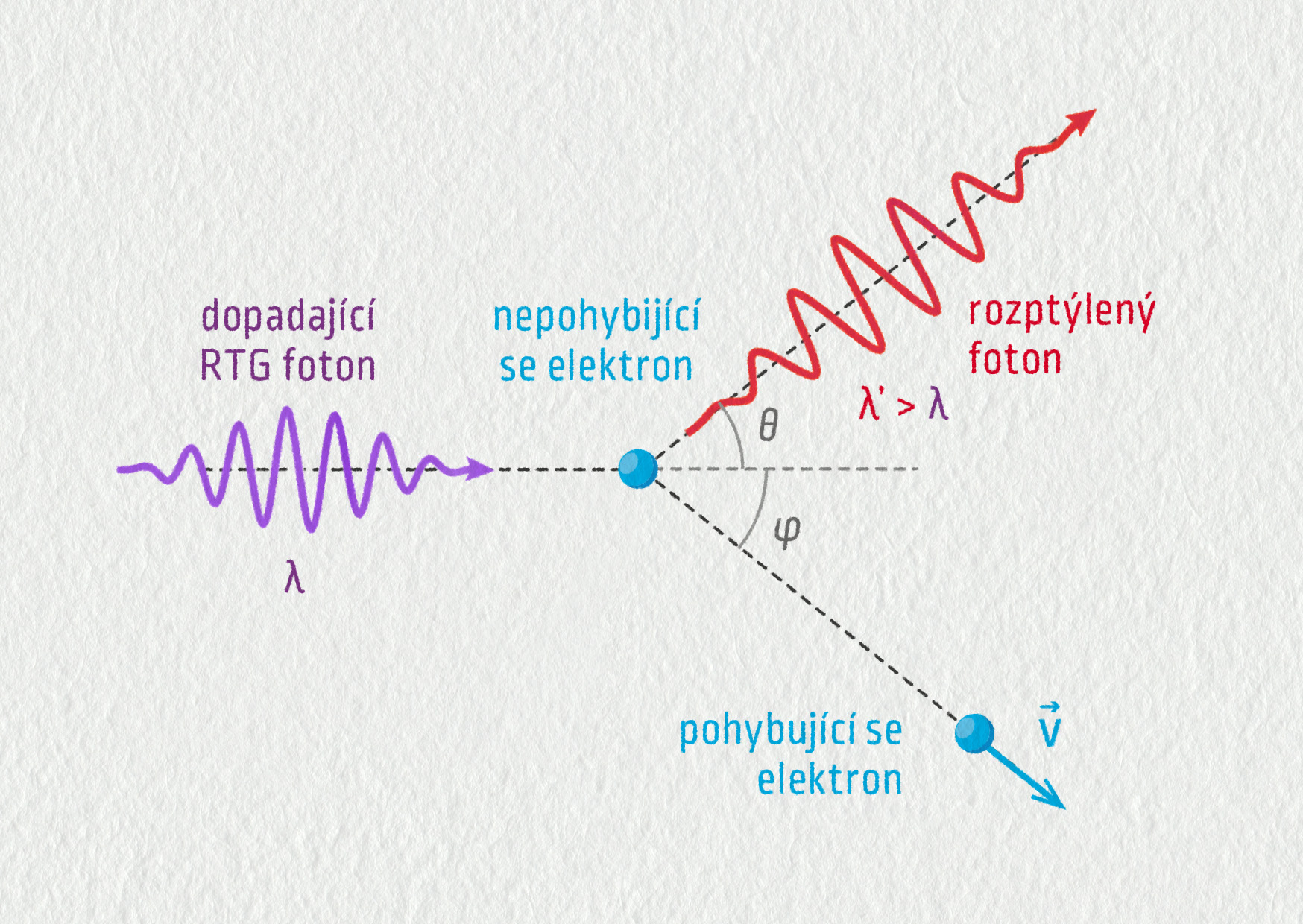
25.15 – Comptonův jev. Rentgenové záření dopadá na uhlíkový terčík (foton RTG záření se sráží s nehybným elektronem). Výsledek experimentu můžeme popsat jako srážku dvou částic s předáním části energie.
Zdroj

Compton vysvětlil rozptyl rentgenových paprsků na uhlíku pomocí fotonů. Na srážku RTG záření a elektronu nahlížíme jako na interakci dvou pevných částic – fotonu a nehybného elektronu. Při této srážce se zachovává energie i hybnost soustavy. Rovnice vyjadřující zákon zachování energie má tvar \(hf=hf'+E_\mathrm{k}\), kde \(hf\) je energie dopadajícího fotonu, \(hf'\) je energie rozptýleného fotonu a \(E_\mathrm{k}\) je kinetická energie elektronu po srážce. Po nárazu má elektron kinetickou energii a rozptýlený foton, který ztratil určitou hodnotu energie, má menší energii. Jeho frekvence je nižší než frekvence dopadajícího fotonu (\(f'<f\)), a vlnová délka naopak vyšší (\(\lambda'>\lambda\)). Jak jsme již zmínili, při této srážce je zachována nejen energie, ale také hybnost, kterou pro pohybující se foton můžeme vyjádřit vztahem

\[ p = \frac{hf}c = \frac{h}{\lambda}\;. \]

Comptonův jev se spolu s vysvětlením fotoelektrického jevu stal jasným důkazem správnosti částicové teorie světla a ta byla v roce 1923 vědeckou společností definitivně přijata.