Vědecká metoda, jakožto způsob objevování našeho světa, je založena na měření. Vědci se snaží měřit co nejpřesněji, tak říkajíc s astronomickou přesností. Pojďme se na přesnost měření podívat podrobněji a společně odhalit nečekané souvislosti.
Začneme jednoduchým příkladem. Před námi leží předmět, dejme tomu papír A4, jehož délku potřebujeme zjistit. Přiložíme krejčovský metr s dílky po jednom centimetru a přečteme hodnotu 30 cm. Když chceme výsledek zpřesnit, místo metru použijeme pravítko s dílky po jednom milimetru, a odečteme hodnotu 29,7 cm.
První údaj byl změřen s přesností na centimetry (krejčovským metrem nemůžeme zjistit přesně, kolik milimetrů), druhý údaj známe přesněji - na milimetry, ale opět nevíme, jaké číslo bude následovat za sedmičkou (kolik desetin milimetrů). Místo pravítka bychom mohli brát stále citlivější měřidla, ale nikdy nemůžeme zjistit číslo na desetinném místě menším, než je nejmenší dílek na použitém měřidle. Tím dospíváme k zásadnímu poznatku: Žádnou veličinu ve fyzice nelze změřit zcela přesně.
Výsledek 30 cm získaný měřením svinovacím metrem znamená, že skutečná délka předmětu je blíže k 30 centimetrům nežli k 29 cm nebo 31 cm, ale nemůžeme rozhodnout, jestli je to 29,7 cm nebo třeba 30,1 cm. Zápis d = 30 cm bez dalšího upřesnění znamená, že správná hodnota délky předmětu leží v intervalu od 29,5 cm do 30,5 cm. Výsledkem měření je interval.
| \(a_\mathrm{m}\) změřená hodnota | například \(a_\mathrm{m}=30\ \mathrm{cm}\) |
| \(\Delta a\) absolutní nejistota měření | například \(\Delta a=0{,}5\ \mathrm{cm}\) |
| \(a=a_\mathrm{m}\pm\Delta a\) interval spolehlivosti | například \(a=(30{,}0\pm0{,}5)\ \mathrm{cm}\) |
Vyjde-li délka papíru dejme tomu 300 mm, zapíšeme ji v cm jako 30,0 cm. Nula za desetinnou čárkou v tomto případě není zbytečná, pomáhá vyjádřit přesnost – odborně se tomu říká počet platných míst. Číslo má tolik platných míst, kolik má číslic, nepočítáme-li nuly na začátku. Údaj 30,0 cm má tři platná místa, můžeme ho takto zapsat v různých jednotkách:
30,0 cm = 300 mm = 0,300 m = 3,00 ⋅ 108 nm (zápis na tři platná místa)
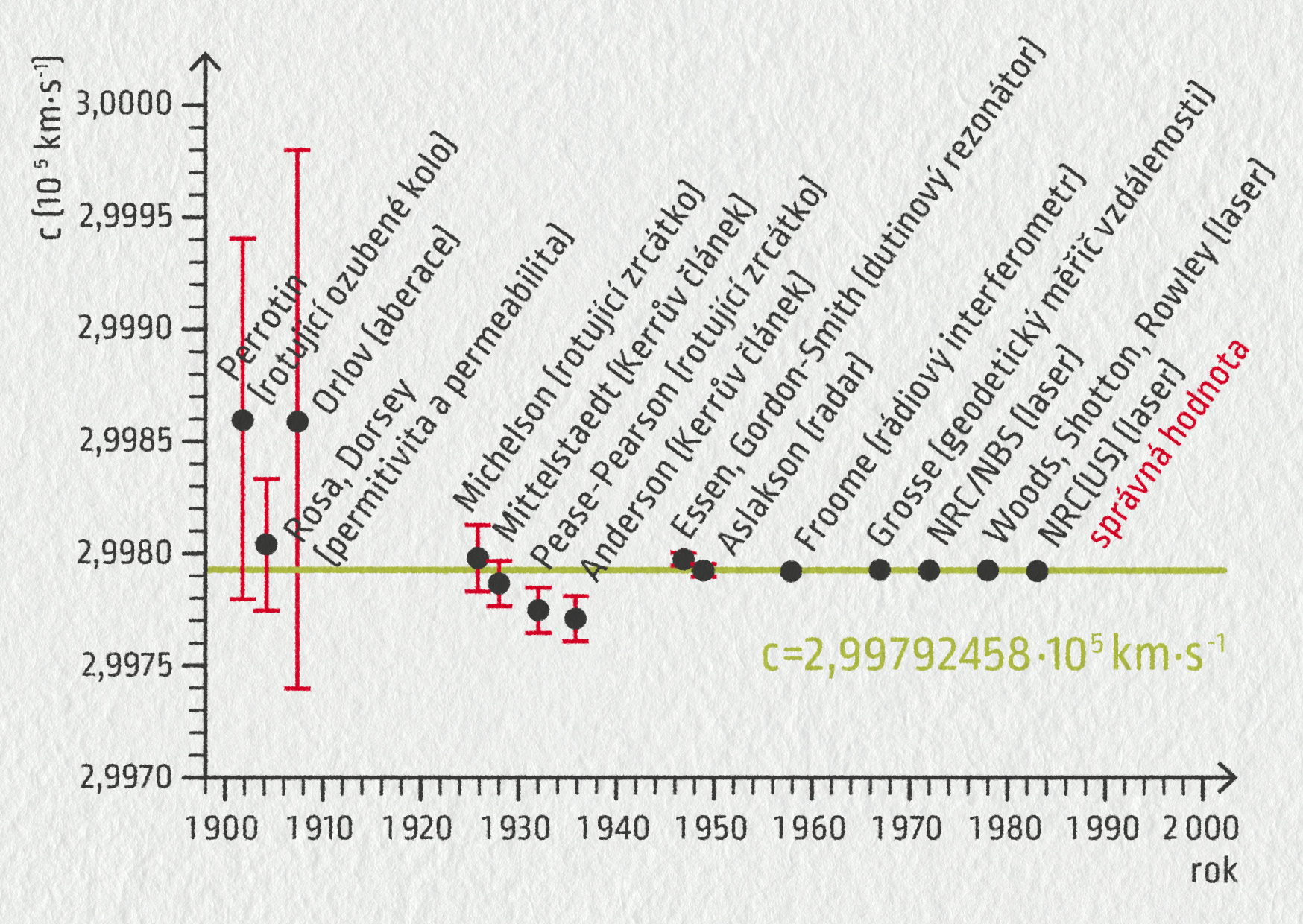
Nejistota měření \(\Delta a\) má stejnou jednotku jako změřená hodnota. V případě odečtu hodnoty na stupnici ji můžeme určit jako polovinu nejmenšího dílku stupnice. U digitálních přístrojů je potřeba nejistotu najít v návodu. V grafech se často nejistota vyznačuje úsečkami, jak můžete vidět na obrázku.
Zdroj
Co je to relativní nejistota?
Když měříme veličinu přesně, znamená to, že nejistota \(\Delta a\) je velmi malá v porovnání s měřenou hodnotou \(a_\mathrm{m}\). Přesnost různých měřicích metod se porovnává pomocí tzv. relativní nejistoty \(\delta a\): Relativní nejistota \(\delta a\) říká, kolik procent z naměřené hodnoty \(a_\mathrm{m}\) zaujímá nejistota \(\Delta a\).
\(\displaystyle \delta a = \frac{\Delta a}{a_\mathrm{m}}\) relativní nejistota měření, například \(\delta d=0{,}5\ \mathrm{cm}/30\ \mathrm{cm}=0{,}017=1{,}7\,\%\)
Často se stane, že potřebujeme určit nejistotu veličiny vypočítané ze změřených hodnot (například určujeme hustotu na základě měření objemu a hmotnosti). V těchto případech určujeme nejistotu výsledku pomocí zákona přenosu nejistoty. Většinou si vystačíme s těmito čtyřmi pravidly:
| \[\begin{aligned}c&=a+b\cr c&=a-b\cr\end{aligned}\] | \[\Delta c=\sqrt{(\Delta a)^2+(\Delta b)^2}\] | Pokud se veličiny sčítají nebo odčítají, pak výslednou absolutní nejistotu určíme jako odmocninu ze součtu druhých mocnin jejich absolutních nejistot. |
| \[\begin{aligned}c&=ab\cr c&=a/b\cr\end{aligned}\] | \[\delta c=\sqrt{(\delta a)^2+(\delta b)^2}\] | Pokud se veličiny násobí nebo dělí, pak výslednou relativní nejistotu určíme jako odmocninu ze součtu druhých mocnin jejich relativních nejistot. |
| \(c=a^n\) | \(\delta c=n\,\delta a\) | Pokud se veličina umocňuje, pak výslednou relativní nejistotu určíme jako n-násobek relativní nejistoty \(\delta a\). |
| \(c=ka\) | \(\Delta c=k\,\Delta a\) | Pokud se veličina násobí konstantou \(k\), pak výslednou absolutní nejistotu určíme jako k-násobek absolutní nejistoty \(\Delta a\). |
Použití těchto pravidel ukazuje následující příklad.
\(\varrho=m/V=21\,415\ \mathrm{kg}\cdot\mathrm{m}^{-3}\). Jelikož \(m\) a \(V\) vystupují v podílu, platí podle pravidla pro počítání s relativními nejistotami: \(\delta\varrho=\sqrt{(\delta m)^2+(\delta V)^2}\).
Relativní nejistoty si musíme nejdřív vypočítat:
\[\begin{aligned} \delta m &=\frac{0{,}1\ \mathrm{g}}{702{,}4\ \mathrm{g}}=0{,}000\,14\;,\\ \delta V &=\frac{0{,}5\ \mathrm{cm}^3}{32{,}8\ \mathrm{cm}^3}=0{,}015\;,\\ \delta\varrho &= \sqrt{(\delta m)^2+(\delta V)^2} = \sqrt{0{,}00014^2 + 0{,}015^2} = 0{,}015\\ \end{aligned}\]Vidíme, že veličina s větší relativní nejistotou (objem) rozhoduje o celkové nejistotě.
Na závěr určíme absolutní nejistotu
\[\Delta\varrho=\varrho\cdot\delta\varrho=21\,415\ \mathrm{kg}\cdot\mathrm{m}^{-3}\cdot0{,}015=321{,}225\ \mathrm{kg}\cdot\mathrm{m}^{-3}\doteq300\ \mathrm{kg}\cdot\mathrm{m}^{-3}\](nejistotu zaokrouhlujeme na jedno, maximálně dvě platná místa).
Teprve teď můžeme správně zaokrouhlit také výslednou hustotu, a to podle výsledné nejistoty: \(\varrho=(21\,400\pm300)\ \mathrm{kg}\cdot\mathrm{m}^{-3}\).
Nyní máme potřebné nástroje také pro dokončení úlohy o měření papíru A4 z úvodu této kapitoly.
Určete plošnou hustotu papíru A4 včetně nejistoty, víte-li, že jeho hmotnost je \(m=(5{,}0\pm0{,}1)\ \mathrm{g}\) a rozměry jsou \(a=(21{,}00\pm0{,}05)\ \mathrm{cm}\), \(b=(29{,}70\pm0{,}05)\ \mathrm{cm}\).
\(\varrho=m/S=m/(ab)=80{,}2\ \mathrm{g/m}^2\).
Poučeni z předchozího příkladu už nemusíme používat zákon přenosu nejistot, neboť vidíme, že relativní nejistota hmotnosti je řádově větší než nejistoty rozměrů \(a\), \(b\). Proto můžeme psát:
\(\delta\varrho=\delta m =0{,}1\ \mathrm{g}/5\ \mathrm{g}=0{,}02\),
\(\Delta\varrho=\varrho\cdot\delta\varrho=80{,}2\ \mathrm{g/m}^2\cdot0{,}02\doteq2\ \mathrm{g/m}^2\)
\(\varrho=(80\pm2)\ \mathrm{g/m}^2\).
Systematická chyba měření
Ne vždy je nejistota měření dána pouze citlivostí přístroje. Často vstupuje do hry ještě systematická chyba, která může naše měření pořádně pokazit, aniž bychom to tušili. Seznámíme se s ní pomocí jednoho experimentu:
V nádobě je trocha octa a na ní nafukovací balónek se sodou (viz obrázek). Nádobu položíme na přesnou váhu a poté vysypeme sodu do octa – balónek se nafoukne. Vidíme, že údaj na váze se změnil. Proč? Může se chemickou reakcí změnit hmotnost? Nebo je na vině nafouknutý balónek? Který údaj na váze představuje skutečnou hmotnost nádoby s balónkem?
Systematickou chybu při vážení způsobuje vztlaková síla působící směrem vzhůru. Kvůli ní váha ukáže vždy menší hodnotu, než odpovídá skutečné hmotnosti nádoby s balónkem. A to i v případě, kdy nebyl balónek nafouknutý. Tuto chybu můžeme odstranit buď tím, že budeme vážit ve vakuu, nebo výpočtem velikosti vztlakové síly podle vzorce a následnou korekcí.
Systematická chyba způsobuje, že všechny měřené hodnoty jsou stejným způsobem posunuté oproti skutečnosti. Například při měření pravítkem může člověk stupnici špatně přikládat k předmětu (lidská chyba) nebo se pravítko při měření za nízké teploty o něco zkracuje (chyba měřidla). Odstranění systematických chyb je velmi důležité, protože bez něj může správná hodnota měřené veličiny ležet zcela mimo interval spolehlivosti. Stejně důležitý je odhad systematických chyb a odpovídající zvětšení nejistoty v případech, kdy není možné systematickou chybu odstranit.

Zdroj
Náhodná chyba měření
Máme-li dostatečně citlivé měřidlo, můžeme odhalit, že jsou naše měření ovlivněna nějakým náhodným vlivem nebo šumem (náhodné otřesy, kolísání napětí v elektronických přístrojích...). Opět si to ukážeme v jednom experimentu:
Učitel dvakrát po sobě tleskne. Vaším úkolem bude změřit stopkami dobu mezi dvěma tlesknutími. Měření bude výrazně ovlivněno reakční dobou člověka, která závisí na jeho momentálním soustředění a je pokaždé trochu jiná. Vliv této náhodné chyby můžeme podstatně zmírnit tím, že budeme měření opakovat – necháme ten samý jev měřit současně víc lidí a jejich výsledky zprůměrujeme.
V tabulce vidíte příklad konkrétních výsledků. Extrémní hodnotu, která se nachází daleko od ostatních, ze zpracování většinou vyřazujeme. U takové hodnoty máme podezření, že došlo k hrubé chybě (omylu).
| Číslo měření | Čas [s] | |
|---|---|---|
| 1 | 3,61 | |
| 2 | 3,69 | |
| 3 | 3,48 | |
| 4 | 3,56 | |
| 5 | 3,04 | vyřazená hodnota |
| 6 | 3,56 | |
| 7 | 3,62 | |
| 8 | 3,60 | |
| 9 | 3,61 | |
| 10 | 3,62 | |
| 11 | 3,51 | |
| 12 | 3,49 | |
| průměr | 3,58 |
Náhodná chyba se projeví rozptýlením hodnot kolem skutečné hodnoty při opakovaném měření. Náhodné vlivy se průměrováním částečně vyruší (na rozdíl od systematické chyby, která posunuje všechny hodnoty stejně). Proto při opakovaném měření, které je zatíženo významnou náhodnou chybou, použijeme aritmetický průměr měřených hodnot.
aritmetický průměr \(\displaystyle x=\frac{x_1+x_2+x_3+\dots+x_n}n=\frac1n\sum_{i=1}^n x_i\)
Vliv systematické a náhodné chyby na soubor měření ukazuje následující graf:
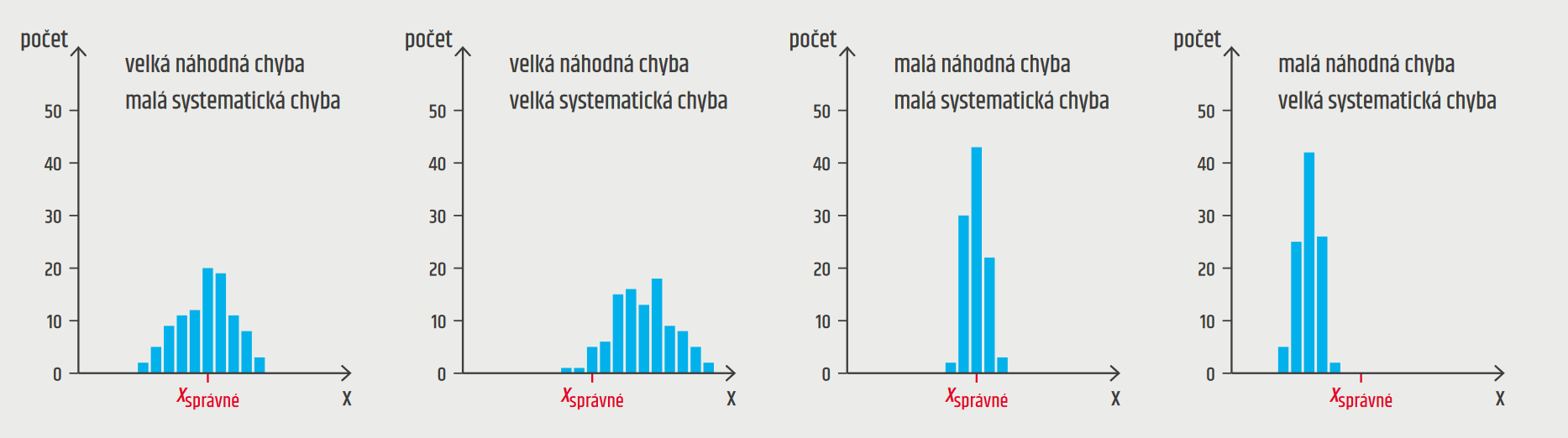
Zdroj
Opakovaná měření zatížená náhodnou chybou jsou v praxi docela častá, proto se dále zpracovávají pomocí statistických metod. Je samozřejmě snahou každého experimentálního fyzika, aby chyby jeho měření byly co nejmenší. Ale na které musí dávat větší pozor? Určitě na systematické! Zatímco náhodné chyby se samy prozradí (při opakovaném měření bude získávat různé hodnoty), systematické chyby opakováním měřením nikdy neodhalí.




