Jak je definován metr?

Zdá se vám samozřejmé, že vzdálenosti měříme v metrech nebo kilometrech? Ne vždy tomu tak bývalo. Na konci 18. století panoval v jednotkách délky chaos. Různé státy používaly své národní jednotky (u nás např. palec, pěst, stopa, loket, sáh, míle atd.). Metrická soustava se objevila poprvé v roce 1790 za Francouzské revoluce, kdy byla vědecká komise pověřena vytvořením zcela nové soustavy jednotek. Tato komise navrhla zavést také novou jednotku délky – metr. Podle ní se ona nová soustava jednotek začala nazývat metrický systém. První definice metru byla tato:

1 metr = jedna desetimilióntina zemského kvadrantu.

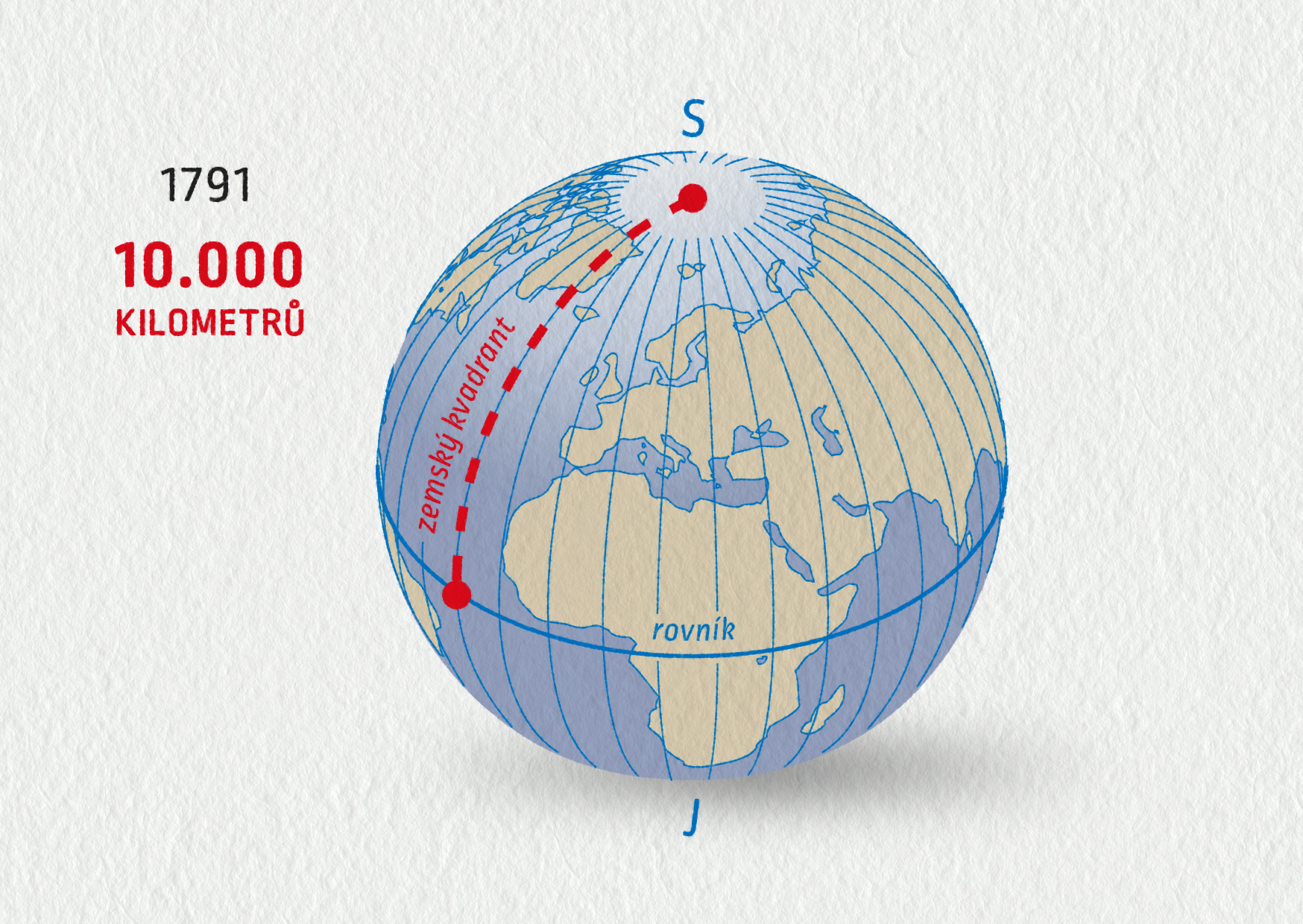
2.5 – Zemský kvadrant je vzdálenosti od pólu k rovníku po idealizovaném zemském povrchu. Tato vzdálenost byla stanovena jako 10 000 km.
Zdroj

Důvodem této volby byla nezávislost na jednotkách vyrobených člověkem. Jak ale určit délku jednoho metru pro praktické účely? To vůbec nebylo jednoduché. Bylo potřeba změřit velikost Země s velkou přesností. Francouzi se o to pokoušeli v letech 1792–1799, kdy geodeti Delambre a Méchain měřili délku poledníku mezi Dunkerque a Barcelonou pomocí triangulace (viz další odstavec). Jejich výsledky nakonec nebyly dost přesné, a proto byli vědci nuceni definovat metr jinak – pomocí tzv. etalonu:

1 metr = délka tyče ze slitiny platiny a iridia, jež byla vyrobena dne 23. června 1799 a uložena ve francouzském národním archivu.

Tak vznikl první etalon metru. Jeho kopírováním pak vznikaly další etalony. Pomocí nich můžeme vyrábět a ověřovat všechna další měřidla používaná v praxi. Podrobněji to ukazuje obrázek.

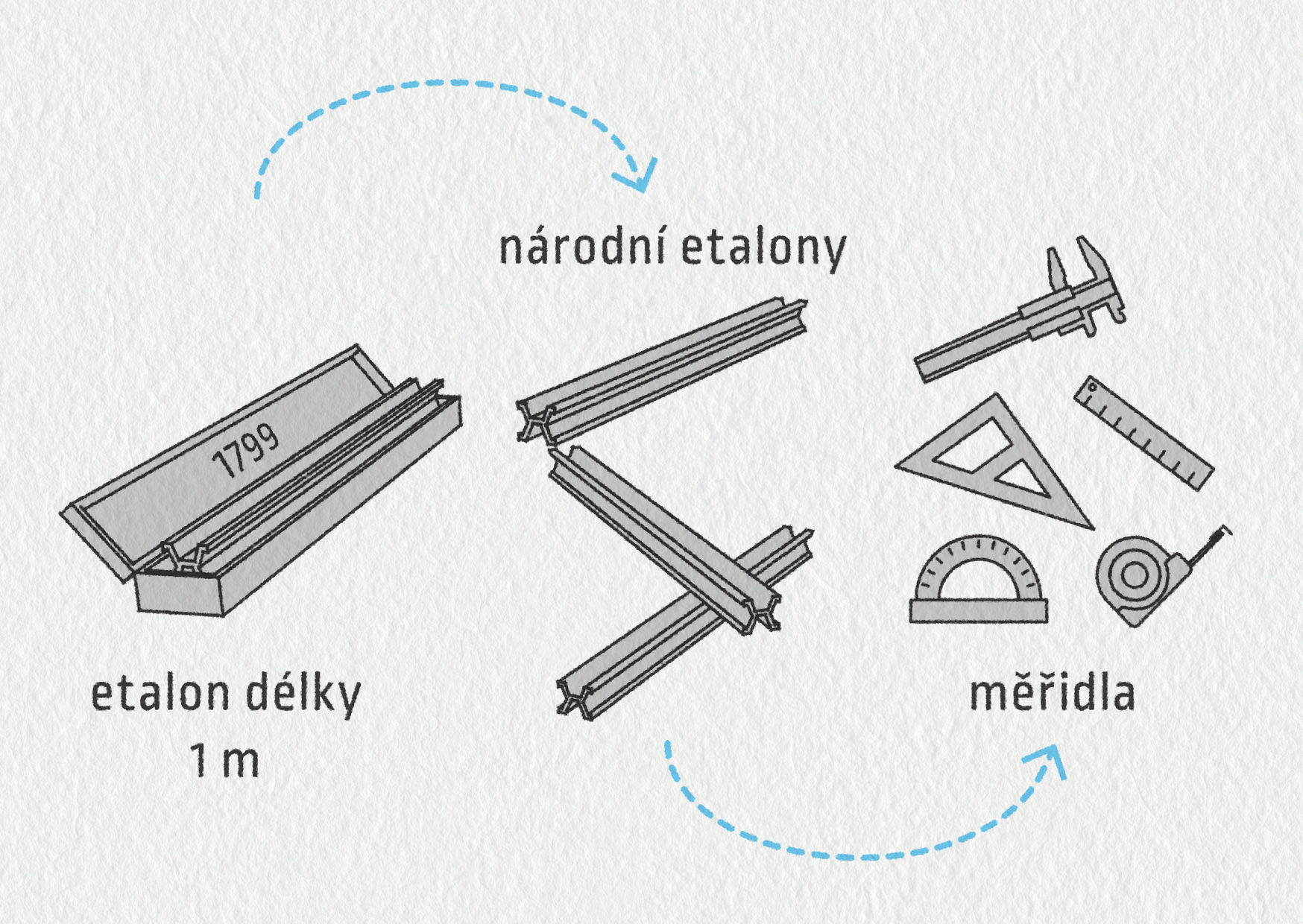
2.6 – Etalon je měřidlo určující danou jednotku. Slouží k uchování této jednotky a jejímu přenosu na další měřidla.
Zdroj

Fyzikové ale stále toužili po univerzální definici, která nebude závislá na konkrétním předmětu. Podařilo se to až v roce 1960 pomocí světla, u kterého dokážeme velmi přesně určit jeho vlastnosti. Definice se opět změnila:

1 metr = 1 650 763,73 násobku vlnové délky světla ve vakuu, které při výboji produkují atomy kryptonu ⁸⁶Kr.

Atomy kryptonu ⁸⁶Kr jsou všechny naprosto stejné, délka jednoho metru je v nich proto „uložena“ lépe a bezpečněji než v platinové tyči. Definice se odkazuje na konkrétní přírodní jev (konkrétní barvu světla vznikající v atomu kryptonu), nikoliv na konkrétní lidský výtvor. Proto je možné při ztrátě či poškození etalonu jednotku vytvořit znovu. S rozvojem fyziky a techniky bylo potřeba měřit fyzikální veličiny stále přesněji. V roce 1983 se tak definice metru ještě jednou změnila:

1 metr = vzdálenost, kterou urazí světlo ve vakuu za 1/299 792 458 sekundy.

Tato definice se odkazuje na rychlost světla a jednotku času – sekundu. Ukázalo se totiž, že čas umíme měřit velmi přesně. Proto bylo výhodnější se při definici metru odkázat na něj. Od roku 2019 platí ještě mírně upravená definice, o níž se můžete dočíst v poznámce Současné definice jednotek SI.

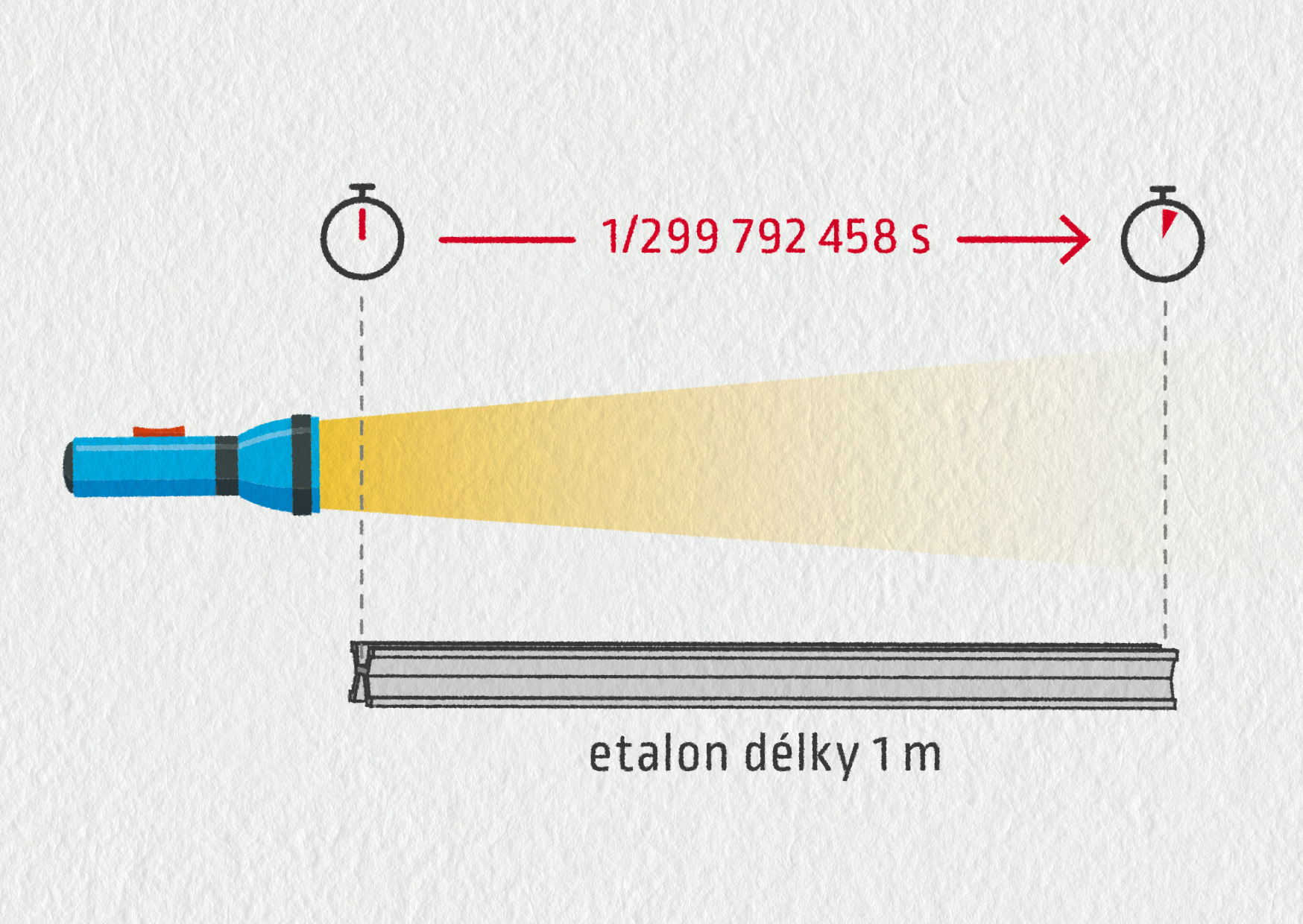
2.7 – Současná definice metru odvozuje jeho délku z rychlosti světla ve vakuu. Obrázek ilustruje pouze princip. Samotné zařízení, které dokáže pomocí světla určit délku metru, vypadá o dost složitěji.
Zdroj

Jak změříme délku v praxi

Nejjednodušším způsobem měření délky je přiložení měřidla (metru, pravítka apod.). To ale není možné v těchto případech: 1) vzdálenost je příliš velká, 2) vzdálenost je příliš malá nebo 3) požadujeme velkou přesnost.

K měření velkých vzdáleností se používá metoda triangulace, která vychází z jednoduché geometrie (viz obrázek). Změříme-li v trojúhelníku délku jedné strany a dva úhly, můžeme délky zbylých stran zjistit rýsováním (věta usu), nebo výpočtem (pomocí goniometrických funkcí nebo sinové věty). Na začátku tedy potřebujeme znát délku jedné úsečky. Dál si už vystačíme jen s měřením úhlů. Pomocí triangulace byly od 18. století zaměřovány základní body, pomocí kterých se sestavovaly a dodnes sestavují mapy.

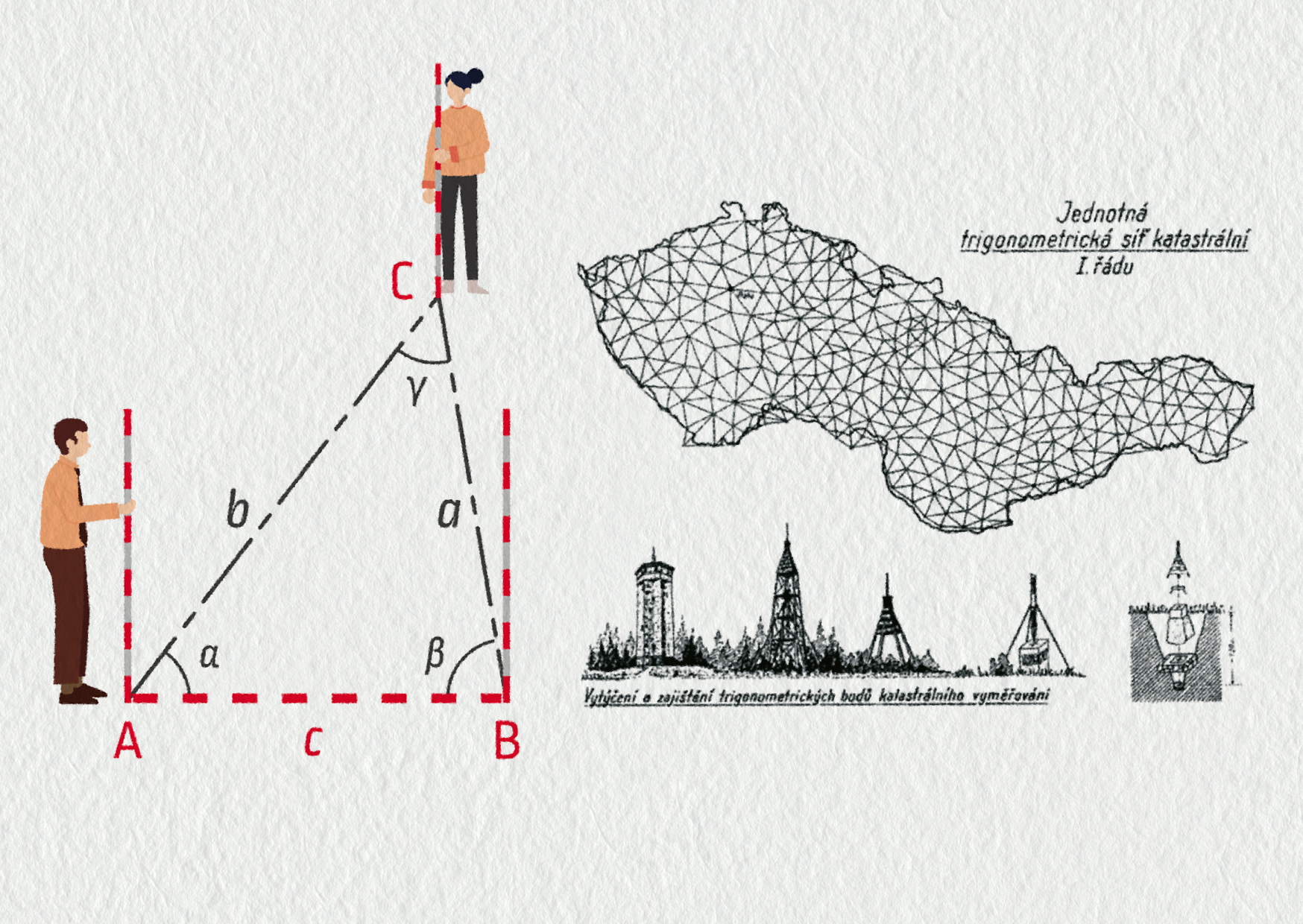
2.8 – Při triangulaci určujeme neznámou vzdálenost pomocí trojúhelníku. Změříme stranu c a úhly alfa a beta. Strany a, b pak můžeme vypočítat. Ilustrace vpravo ukazuje jednotnou trigonometrickou síť katastrální I. řádu z roku 1936.
Zdroj

Triangulaci je možné použít také k určování vzdáleností hvězd (viz obrázek níže).

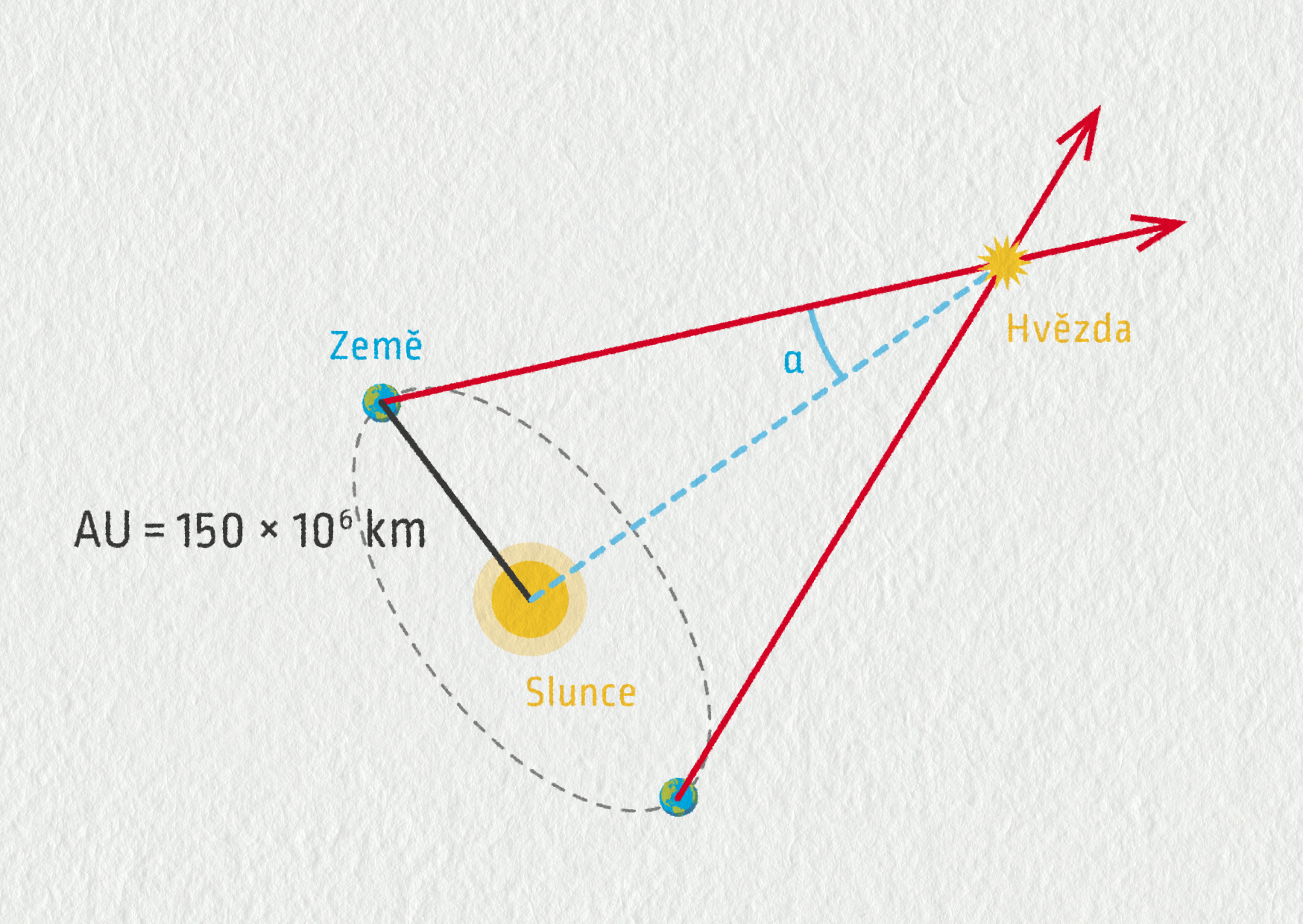
2.9 – Triangulaci můžeme využít k měření vzdálenosti hvězdy od Slunce. Princip metody je naznačen na obrázku. Hvězdy jsou od nás velmi daleko, proto je tato metoda velmi citlivá na přesnost měření – úhly změřené ze Země budou velmi blízké 90°.
Zdroj

Další často využívaná metoda měření vzdálenosti využívá šíření světla nebo zvuku prostorem. Ukážeme si to na příkladu sonaru - uspořádání vidíte na obrázku. Sonar vyšle krátký zvukový puls a měří čas t, za který se vrátí zpět zvuk odražený od překážky. Díky známé rychlosti zvuku ve vzduchu za běžných podmínek (v = 340 m/s), můžeme určit vzdálenost překážky jako \(d = v · \tfrac{t}{2}\) (dělíme dvěma, neboť zvuk se šíří tam a zpět). Po detekci odraženého signálu může být vyslán další puls atd. To se může velmi rychle opakovat, vzdálenost můžeme měřit třeba stokrát za sekundu.

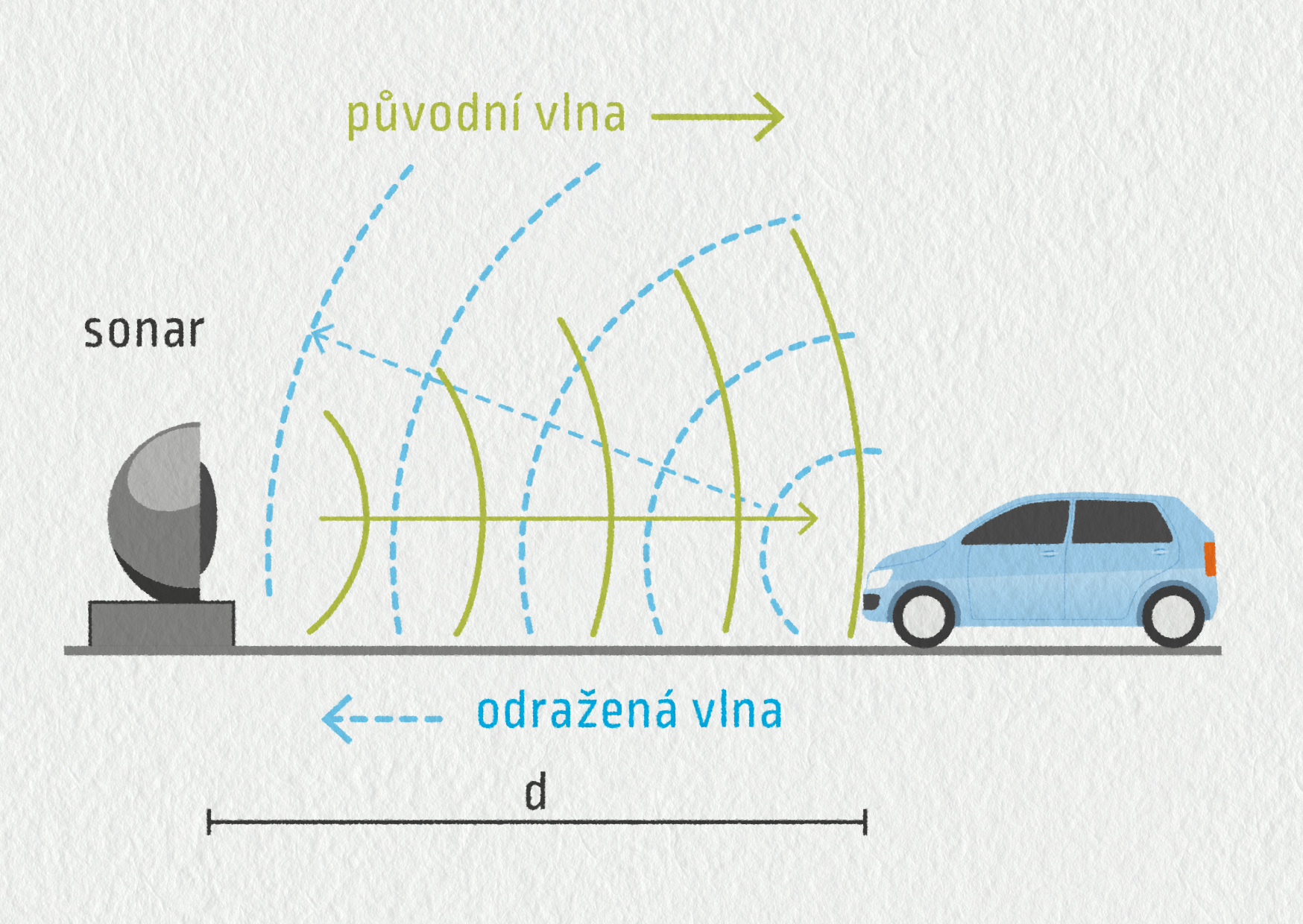
2.10 – Sonar měří vzdálenost objektu pomocí doby, za kterou se vrátí zpět odražená zvuková vlna.
Zdroj

Zařízení, které využívá místo zvuku světlo (obecně elektromagnetické vlny), se nazývá radar. Radar musí měřit čas mnohem přesněji, neboť světlo je asi milionkrát rychlejší než zvuk (rychlost šíření světla ve vakuu je cca 300 000 000 m/s).

Kontrolní otázka

Zvukový signál sonaru se vrátil zpět po odrazu od autíčka za 0,004 s. Jak daleko je autíčko od sonaru? Napište hodnotu v metrech a počítejte s rychlostí zvuku 340 m/s.

Kontrolní otázka

Signál radaru se vrátil zpět po odrazu od letadla za 0,000 08 ms. Jak daleko je letadlo od radaru? Napište hodnotu v km.