Na začátku této kapitoly jsme se naučili odlišovat posuvný a otáčivý pohyb těles. Tělesa vykonávající posuvný pohyb mají pohybovou energii \(E_\mathrm{kT}=\frac{1}{2}mv^2\), kde \(m\) je hmotnost celého tělesa a \(v\) rychlost těžiště.
Zdroj
Podobně je i s otáčením těles kolem pevné osy spojena pohybová energie. Říkáme jí pohybová energie otáčivého pohybu, nebo kinetická energie rotační a značíme \(E_\mathrm{kR}\). Tato energie je rovna práci, kterou je třeba vykonat, abychom těleso z klidu roztočili na úhlovou rychlost \(\omega\). Vypočítáme ji podle vztahu
\[ E_\mathrm{kR} = \frac{1}{2}J\omega^2\;, \]kde \(\omega\) je úhlová rychlost otáčení tělesa a \(J\) moment setrvačnosti tělesa vzhledem k dané ose. Moment setrvačnosti charakterizuje rozložení hmoty kolem osy otáčení a má jednotku kg ⋅ m2.
Zdroj
Kontrolní otázka
Kontrolní otázka
V tabulce 16.38 najdete vztahy pro moment setrvačnosti u některých homogenních a symetrických těles o hmotnosti \(m\). Tyto vzorce se nemusíte učit nazpaměť, nejsou to vztahy základního významu. Možná si je jednou odvodíte, až budete umět integrovat 😉
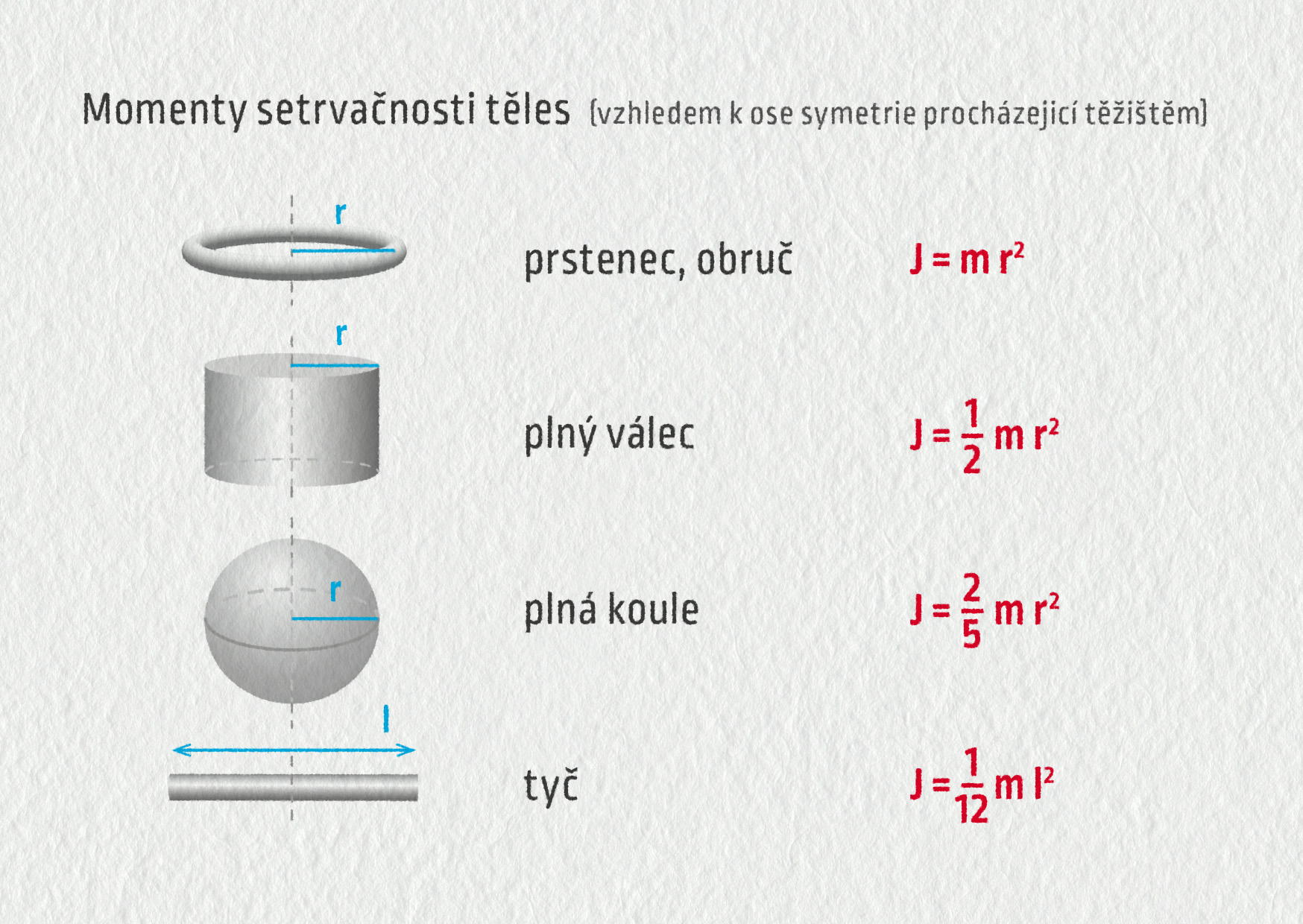
Zdroj
Poznámka na okraj: Odvození vztahu pro rotační kinetickou energii
Předpokládejme, že tuhé těleso se rovnoměrně otáčí úhlovou rychlostí \(\omega\) kolem pevné osy. Atomy, z nichž je vytvořeno a jejichž počet je \(N\), se pohybují po kruhových trajektoriích.
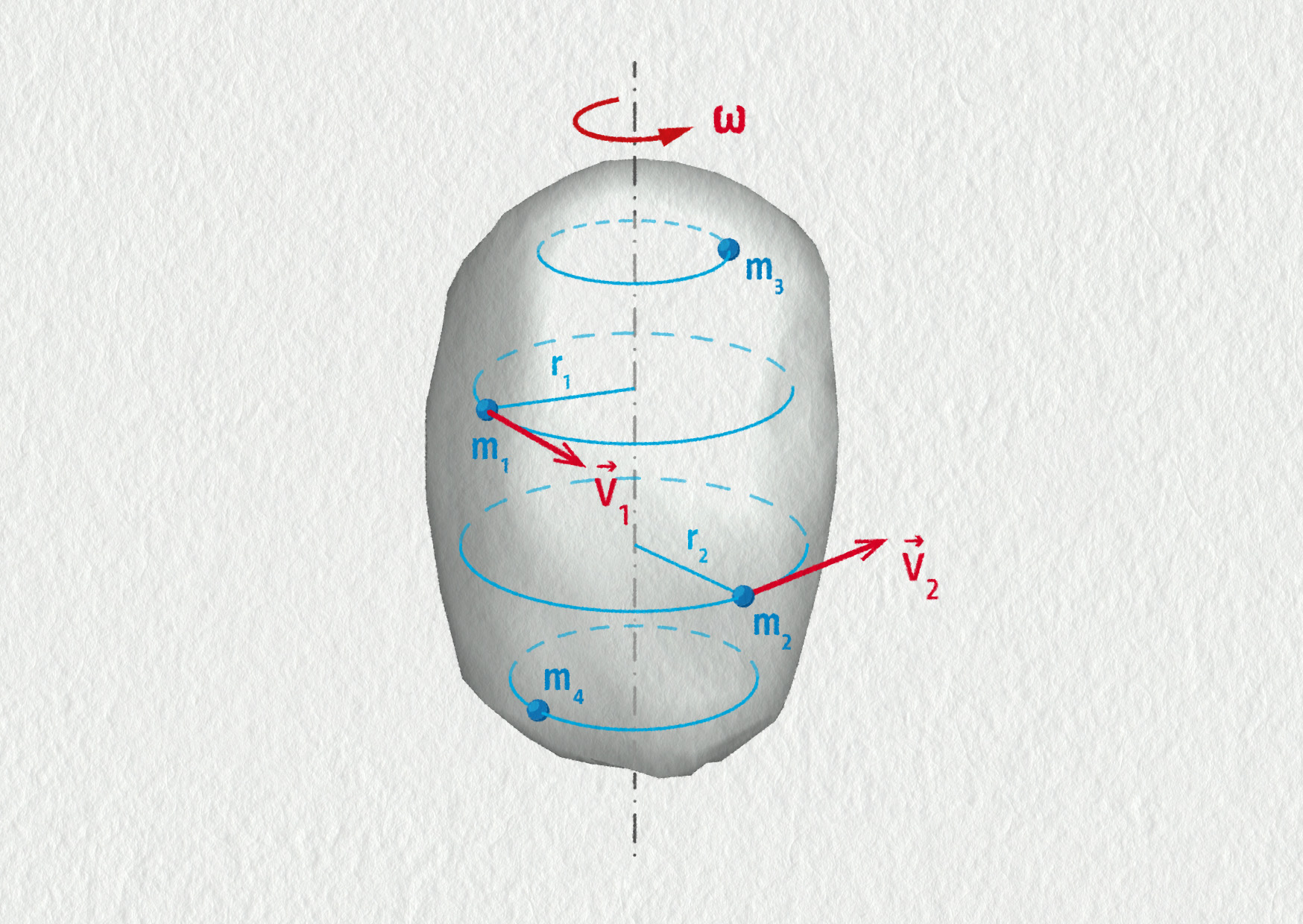
Zdroj
Celkovou pohybovou energii otáčejícího se tělesa získáme jako součet pohybových energií jednotlivých atomů:
\[ E_\mathrm{kR} = E_{\mathrm{k}1} + E_{\mathrm{k}2} + E_{\mathrm{k}3} + \dots + E_{\mathrm{k}N}\;. \]Atomy můžeme považovat v tomto modelu za hmotné body, proto za jejich pohybové energie dosadíme
\[ E_{\mathrm{k}i} = \frac{1}{2}m_iv_i^2\;, \]kde \(m_i\) a \(v_i\) jsou hmotnost a velikost rychlosti i-tého atomu. Máme tedy
\[ E_\mathrm{kR} = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2 + \frac{1}{2}m_3v_3^2 + \dots + \frac{1}{2}m_Nv_N^2\;. \]Třebaže poloměr trajektorie r i velikost rychlosti v jsou pro každý atom jiné, všechny se otáčejí stejnou úhlovou rychlostí \(\omega\), takže rychlost i-tého atomu závisí jen na jeho vzdálenosti od osy otáčení a platí \(v_i=\omega r_i\). Dosadíme do předchozího vztahu
\[ E_\mathrm{kR} = \frac{1}{2}m_1\omega^2r_1^2 + \frac{1}{2}m_2\omega^2r_2^2 + \frac{1}{2}m_3\omega^2r_3^2 + \dots + \frac{1}{2}m_N\omega^2r_N^2\;. \]Ve všech členech se vyskytuje faktor \(\frac{1}{2}\omega^2\), který vytkneme před závorku, a dostáváme
\[ E_\mathrm{kR} = \frac{1}{2}\left(m_1r_1^2 + m_2r_2^2 + m_3r_3^2 + \dots + m_Nr_N^2\right) \omega^2\;. \]Součet členů \(m_ir_i^2\) v kulaté závorce závisí jen na tom, jak je hmotnost rozložena kolem osy otáčení. Pro tuhé těleso točící se kolem osy neměnící směr je to konstanta. Tento součet přes všechny atomy tělesa označíme písmenem \(J\) a budeme nazývat momentem setrvačnosti tělesa vzhledem k dané ose.
\[ J = m_1r_1^2 + m_2r_2^2 + m_3r_3^2 + \dots + m_Nr_N^2\;. \]Odtud již plyne dokazovaný vztah pro pohybovou energii rotujícího tělesa
\[ E_\mathrm{kR} = \frac{1}{2}J\omega^2\;. \]
Pokud koná těleso složený pohyb z posouvání a otáčení, k jeho pohybové energii přispívá jak translační, tak rotační složka
\[ E_\mathrm{k} = E_\mathrm{kT} + E_\mathrm{kR}\;. \]
Příklad 1
Kulička o poloměru 2 cm a hmotnosti 90 g se po podložce kutálí rychlostí o velikosti 2 m/s. Vypočítejte její pohybovou energii.
Při valení po podložce se posouvá těžiště kuličky rychlostí 2 m/s. Kulička se při tom otáčí kolem svého středu. Její pohyb je tedy složený z translace a rotace.
Pohybová energie spojená s translací je
\[ E_\mathrm{kT} = \frac{1}{2}mv^2 = \frac{1}{2}\cdot0{,}090\cdot2^2\ \mathrm{J} = 0{,}18\ \mathrm{J}\;. \]K určení rotačního příspěvku si nejdříve spočítáme moment setrvačnosti
\[ J = \frac{2}{5}mr^2 = \frac{2}{5}\cdot0{,}090\cdot0{,}02^2\ \mathrm{kg\cdot m^2}=0{,}000\,014\,4\ \mathrm{kg\cdot m^2} \]a úhlovou rychlost otáčení
\[ \omega = \frac{v}{r} = \frac{2}{0{,}02}\ \mathrm{rad/s} = 100\ \mathrm{rad/s}\;. \]Pohybová energie spojená s rotací je tedy
\[ E_\mathrm{kR} = \frac{1}{2}J\omega^2 = \frac{1}{2}\cdot0{,}000\,014\,4\cdot100^2\ \mathrm{J}=0{,}072\ \mathrm{J}\;. \]Celková pohybová energie kuličky je
\[ E_\mathrm{k} = E_\mathrm{kT} + E_\mathrm{kR} = 0{,}18\ \mathrm{J} + 0{,}072\ \mathrm{J} = 0{,}252\ \mathrm{J}\;. \]
Kontrolní otázka
Zatímco rám kola se pohybuje posuvným pohybem, přední a zadní kolo koná pohyb složený – jejich těžiště se posouvá dopředu, kola se navíc otáčejí kolem své osy. Celková pohybová energie bude tedy větší než \(E_\mathrm{kT}=\frac{1}{2}mv^2\) právě díky kinetické energii spojené s otáčením kol.
