Působištěm tíhové síly \(\Vec{F}_\mathrm{G}\) je těžiště. Tíhová síla je výslednice gravitační síly působící na těleso u povrchu Země a odstředivé síly, která je dána rotací Země. Přesnější vysvětlení najdete v 17. kapitole. Podívejme se nyní podrobněji, jak je to s jejím působištěm a jak se dá prakticky i výpočtem najít poloha těžiště.
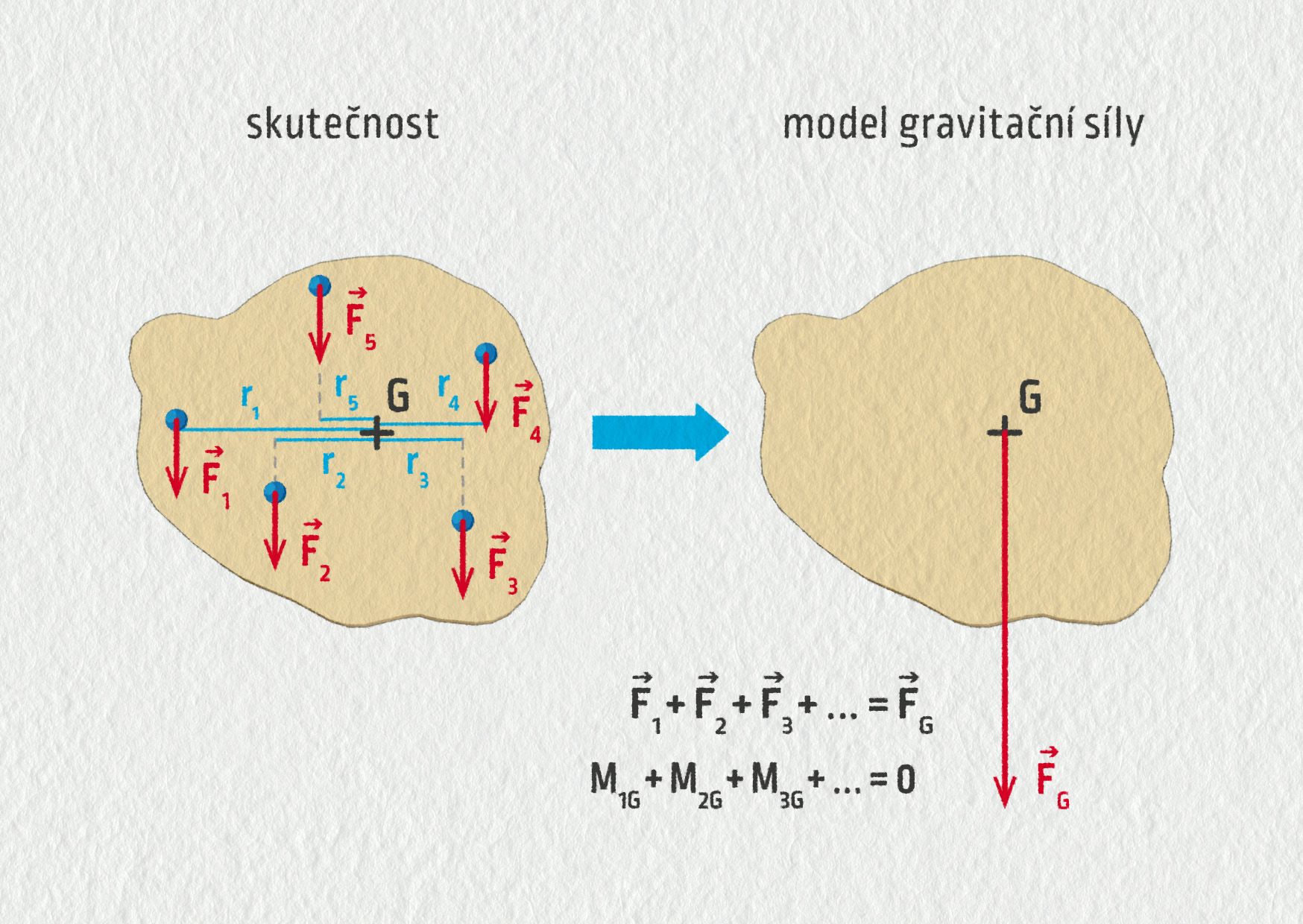
Těžiště tělesa budeme značit písmenem G (center of gravity, le centre de gravité). Pro dané těleso je to jediný bod, vůči kterému má gravitační působení nulový otáčivý účinek. Jak je znázorněno na obrázku 16.21, gravitační síla ve skutečnosti působí na každý atom tělesa. Atomů je ovšem v tělese obrovské množství, např. v 1 cm3 železa je jich řádově 1023. Z praktických důvodů proto tyto mikroskopické síly nahrazujeme jediným vektorem \(\Vec{F}_\mathrm{G}\), jehož působištěm je těžiště. Těžiště G má tu vlastnost, že momenty všech mikroskopických gravitačních sil vztažené k ose procházející bodem G se dohromady přesně vyruší.
Zdroj
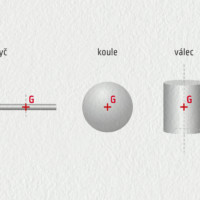
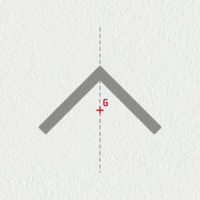
Jak prakticky najít polohu těžiště
Zdroj
Zdroj

Zdroj

Zdroj
Pokud je těleso umístěno v homogenním gravitačním poli (gravitace působí na určité těleso ve všech místech stejně), můžeme souřadnice těžiště určit výpočtem. Zvolíme si soustavu souřadnic, do ní pevně umístíme těleso a vypočítáme vážený průměr souřadnic jednotlivých součástí.
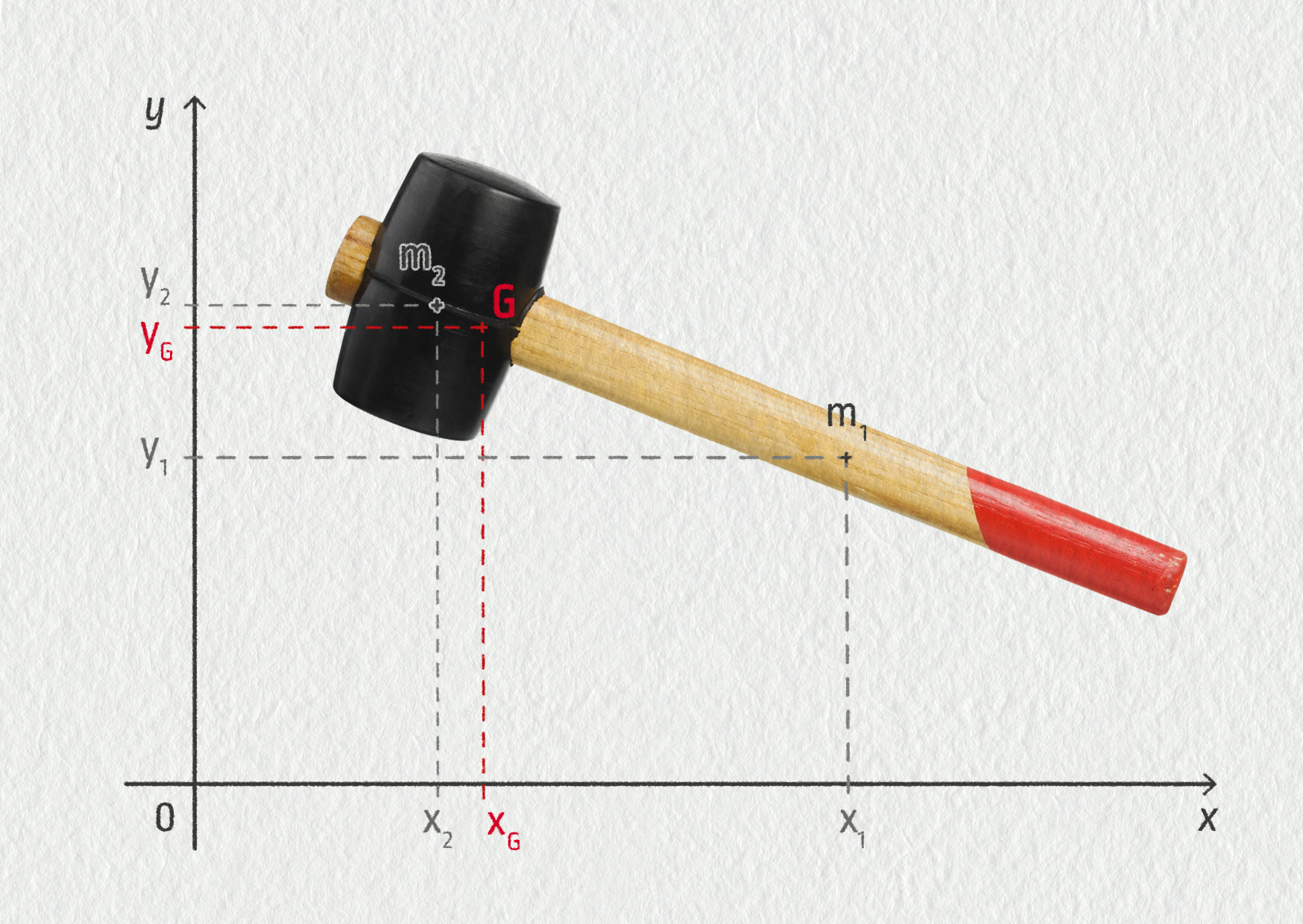
Palička na obrázku 16.23 má dvě základní součásti: dřevěné topůrko o hmotnosti \(m_1\), jehož těžiště má souřadnice \((x_1,y_1)\), a gumovou hlavu o hmotnosti \(m_2\), jejíž těžiště má souřadnice \((x_2,y_2)\).
Zdroj
Souřadnice \((x_G,y_G)\) těžiště celého tělesa vypočítáme jako vážený průměr souřadnic jeho součástí:
\[ x_G = \frac{m_1x_1+m_2x_2}{m_1+m_2} \quad\hbox{a}\quad y_G = \frac{m_1y_1+m_2y_2}{m_1+m_2}\;. \]Zobecnění na těleso tvořené více součástmi se ve vzorcích projeví přidáním dalších sčítanců.
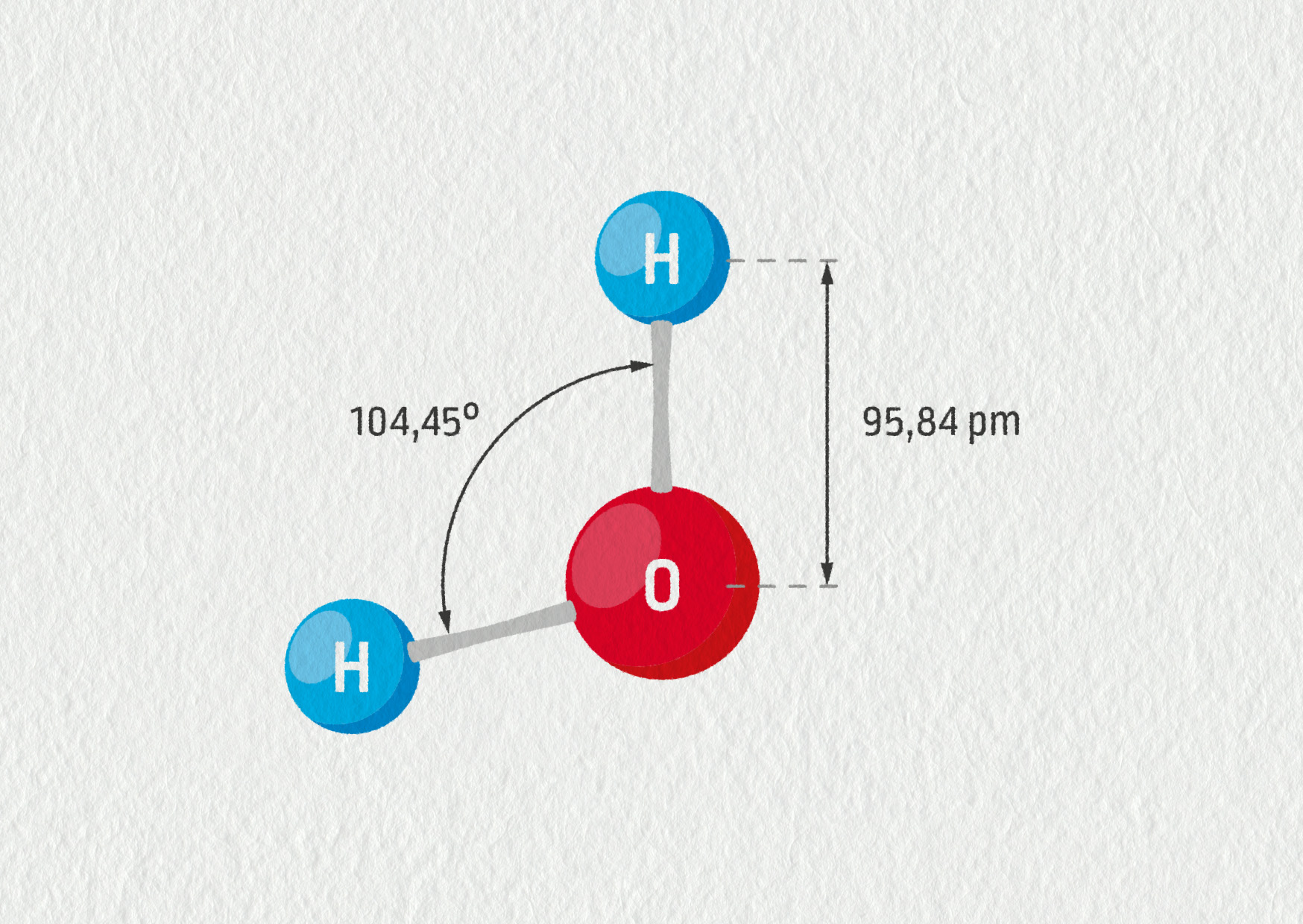
Určete polohu těžiště molekuly vody. Rozměry molekuly H2O jsou patrné z obrázku 16.24. Atomová relativní hmotnost vodíku je 1 a kyslíku 16.
Zdroj
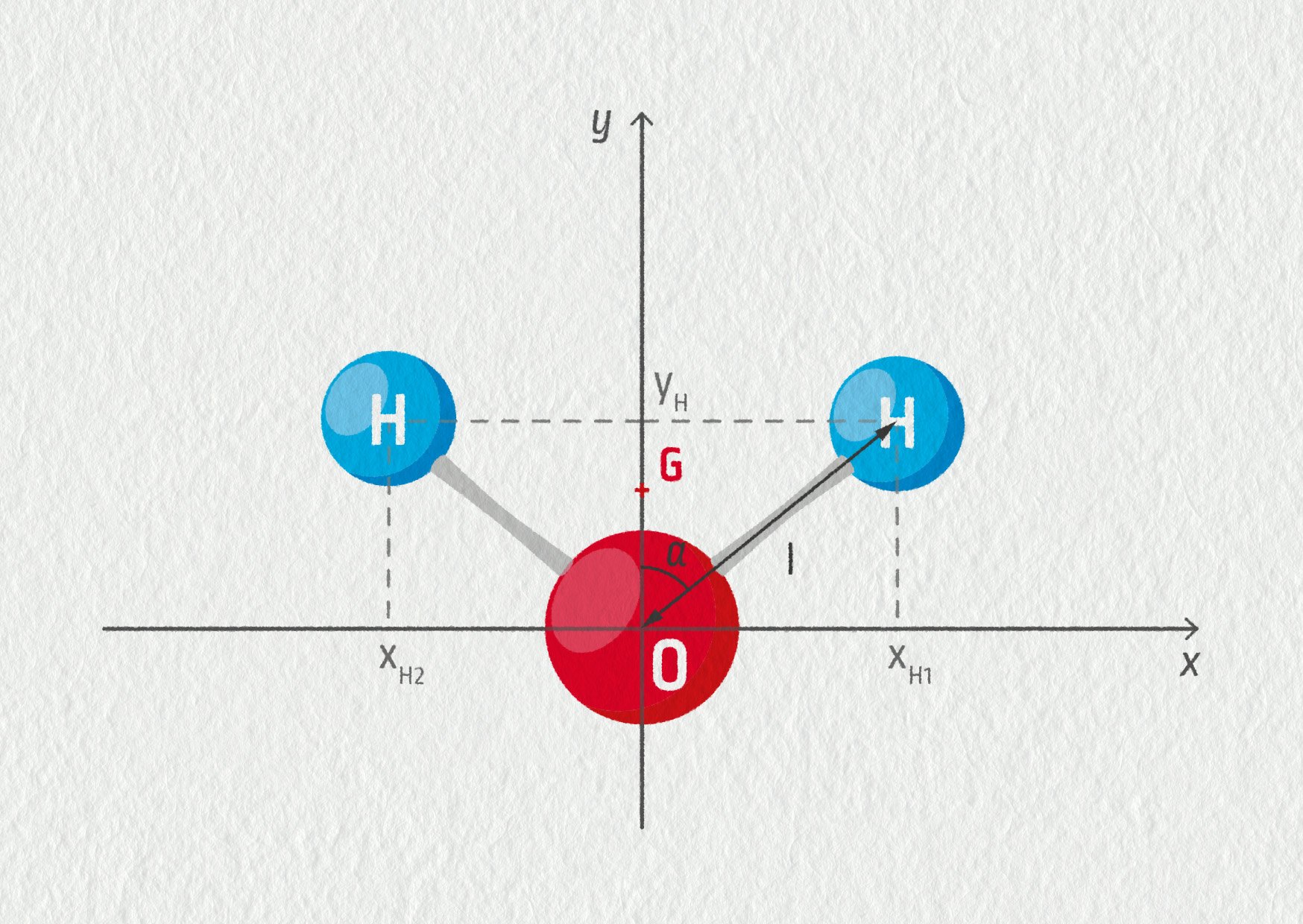
Je zřejmé, že molekula vody je souměrná podle roviny procházející atomem kyslíku. V této rovině bude ležet i její těžiště. Umístíme-li tedy molekulu v soustavě souřadnic tak, jak je naznačeno na obrázku 16.25, bude x-ová souřadnice těžiště \(x_G=0\).
Zdroj
Svislou souřadnici atomů vodíku vypočítáme z naznačeného pravoúhlého trojúhelníka o přeponě \(l\):
\[ \begin{aligned} \alpha&=104{,}45^\circ/2 = 52{,}23^\circ\\ l&=95{,}84\ \mathrm{pm}\\ \cos\alpha&=\frac{y_\mathrm{H}}{l} \quad\Rightarrow\quad y_\mathrm{H}=l\cos\alpha=58{,}70\ \mathrm{pm}\\ \end{aligned} \]Potom stačí jen dosadit do vzorce pro \(y_G\):
\[ y_G = \frac{m_\mathrm{H}y_\mathrm{H}+m_\mathrm{H}y_\mathrm{H}+m_\mathrm{O}y_\mathrm{O}}{m_\mathrm{H}+m_\mathrm{H}+m_\mathrm{O}} = \frac{1\cdot58{,}70\ \mathrm{pm}+1\cdot58{,}70\ \mathrm{pm}+16\cdot0}{1+1+16} = 6{,}52\ \mathrm{pm}\;. \]Těžiště molekuly vody tedy leží na ose symetrie molekuly ve vzdálenosti 6,52 pm od středu atomu kyslíku.
Proč je výsledek správně, třebaže jsme hmotnost nedosadili v základních jednotkách – kilogramech?
Těleso vykonávající posuvný pohyb můžeme modelovat hmotným bodem – uvažujeme jen pohyb jeho těžiště. V mnoha běžných případech (například válení) těleso vykonává složený pohyb, přižemž osa otáčení není pevně fixována. Pohyb takového tělesa můžeme rozdělit na translaci těžiště a rotaci vůči ose procházející těžištěm. Momenty sil potom zcela logicky počítáme vůči těžišti.
Jak se řídí loď.
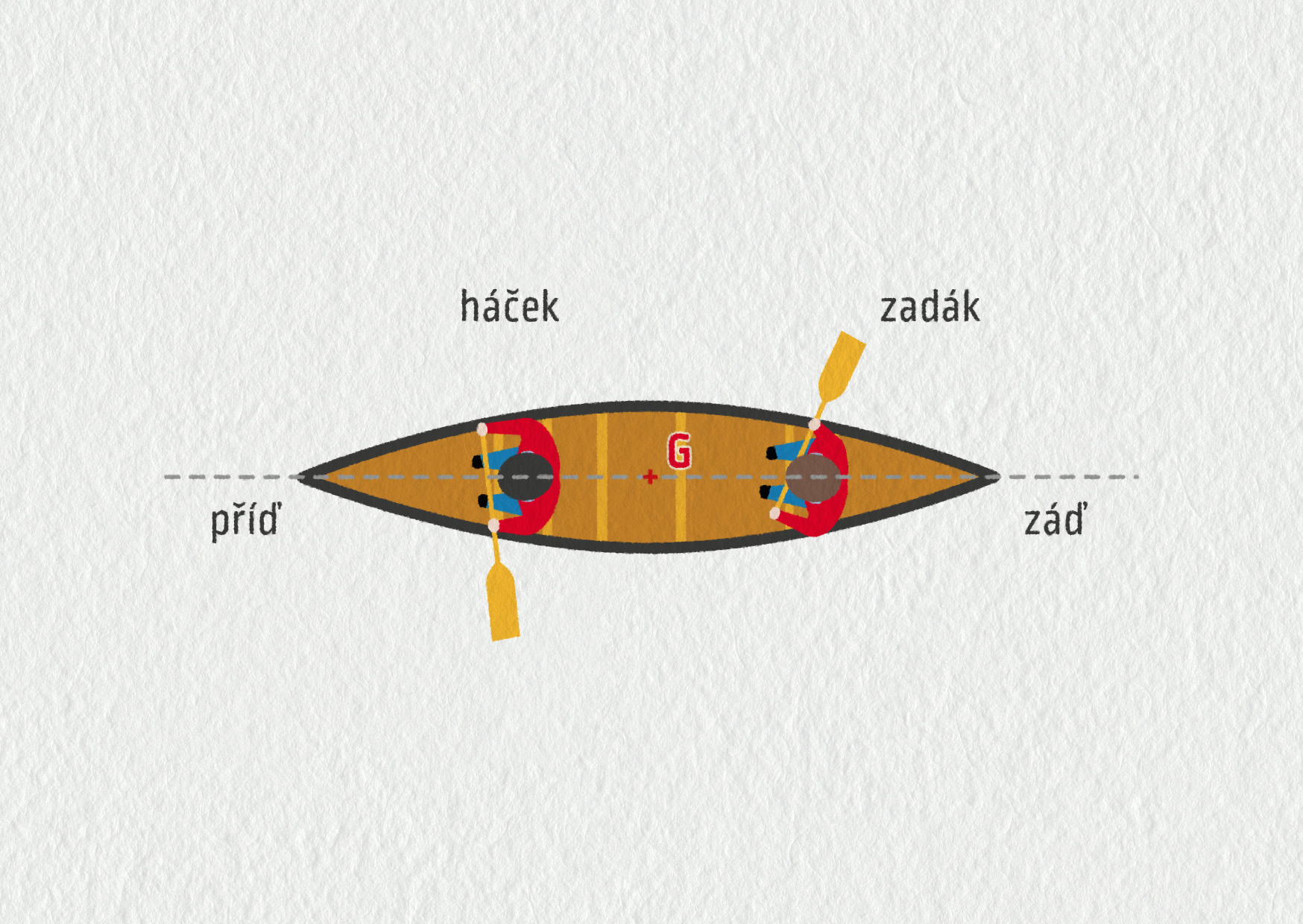
Na obrázku 16.26 je znázorněna kánoe při pohledu shora. Háček je připraven pádlovat vlevo, zadák vpravo. Předpokládejme, že ve sledovaný okamžik se loď nepohybuje vůči vodě, tzn. buď stojí na místě v klidné vodě, nebo má přesně rychlost proudu.
1) Vysvětlete, co způsobí, když
- zadák zabere pádlem rovnoběžně s osou lodi,
- háček i zadák budou pádlovat rovnoběžně s osou lodi.
2) Zadák je v lodi sám. Vysvětlete, jak musí pádlovat, aby mu jela loď rovně.
Zdroj
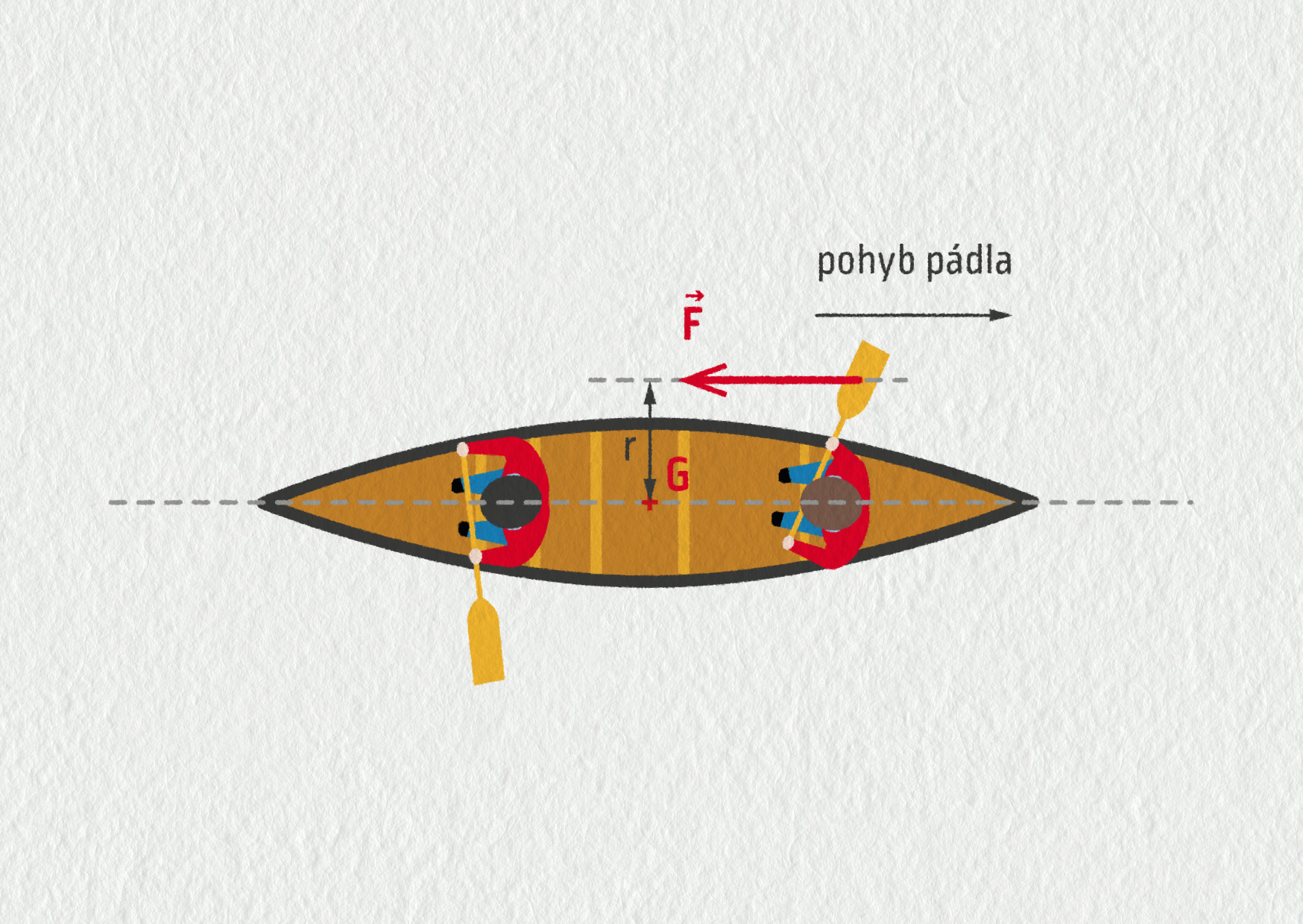
1a) Pádlo se ve vodě pohybuje od přídě k zádi. Tlačí před sebou vodu směrem dozadu silou o velikosti \(F\). Podle třetího Newtonova zákona působí rovněž voda na pádlo silou. Její velikost je \(F\), orientace směrem dopředu (znázorněna v obrázku 16.27 červeně).
Tato síla způsobí zrychlení lodi směrem dopředu. Kromě toho má síla \(F\) nenulový moment vůči těžišti \(M_G=rF\ne0\), takže se loď při každém záběru otočí o určitý úhel kolem těžiště (proti směru hodinových ručiček). Pokud tedy bude zadák pádlovat rovnoběžně s osou lodi, pojede dopředu a při tom bude zatáčet doleva.
Zdroj
Poznámka: Zrádnost této úlohy spočívá v tom, že při vyšetřování pohybu tělesa musíme uvažovat pouze síly, kterými okolí (voda) působí na naše vybrané těleso (kánoe s vodáky). Naopak síly, kterými naše těleso působí na své okolí, nás nezajímají, protože ovlivňují pohyb okolních těles (která nestudujeme).
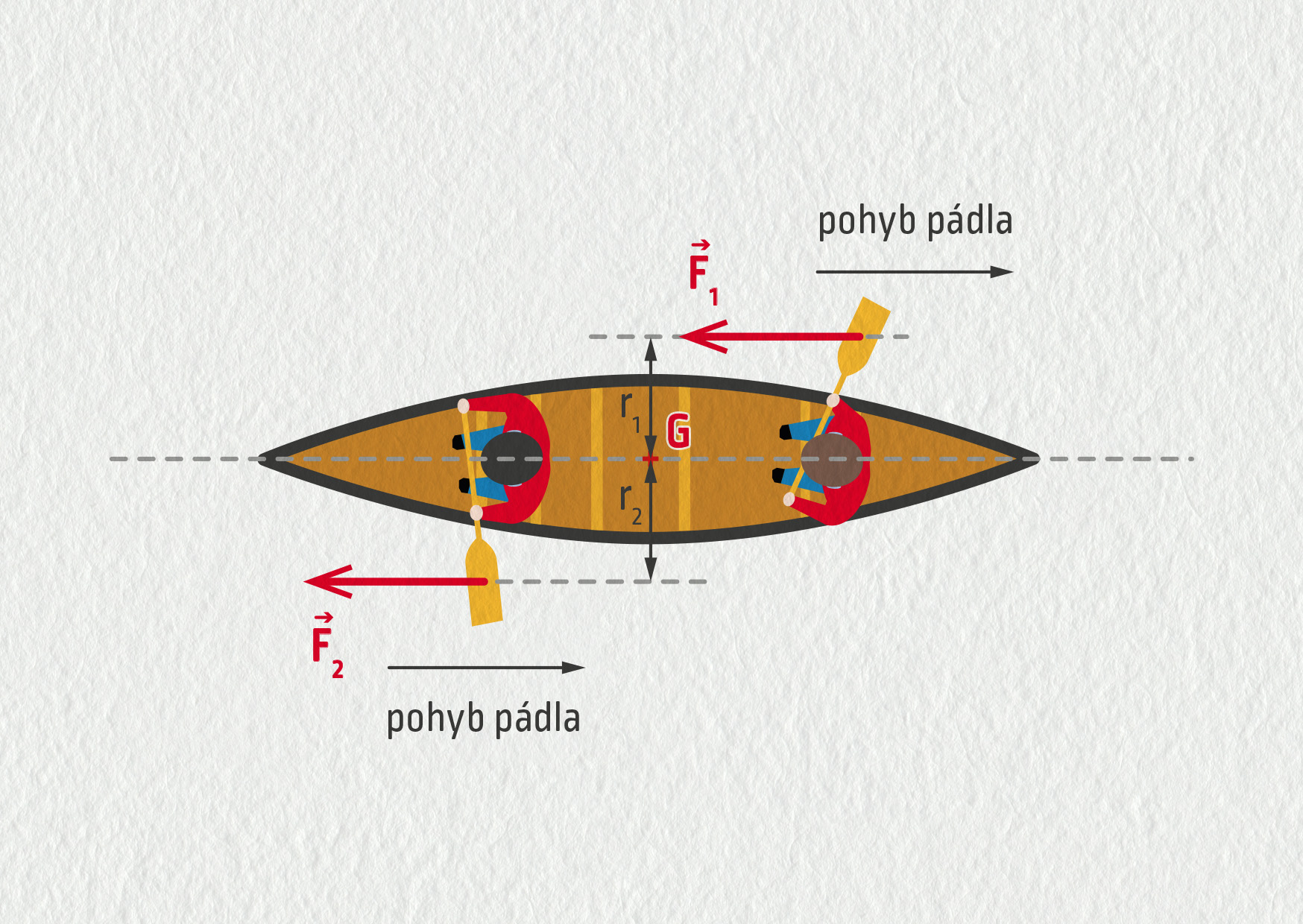
1b) Pro zadáka se situace nezměnila, v obrázku 16.28 je příslušná síla označena \(\Vec{F}_1\). Háček tlačí na vodu pádlem dozadu, takže voda na jeho pádlo silou \(\Vec{F}_2\) směrem dopředu. Tato síla přispívá ke zrychlování lodi směrem dopředu. Její moment \(M_{2G}\) otáčí lodí kolem těžiště ve směru hodinových ručiček, proti momentu \(M_{1G}\) síly \(\Vec{F}_1\). Pokud tyto momenty budou stejně velké, pojede loď rovně.
Zdroj
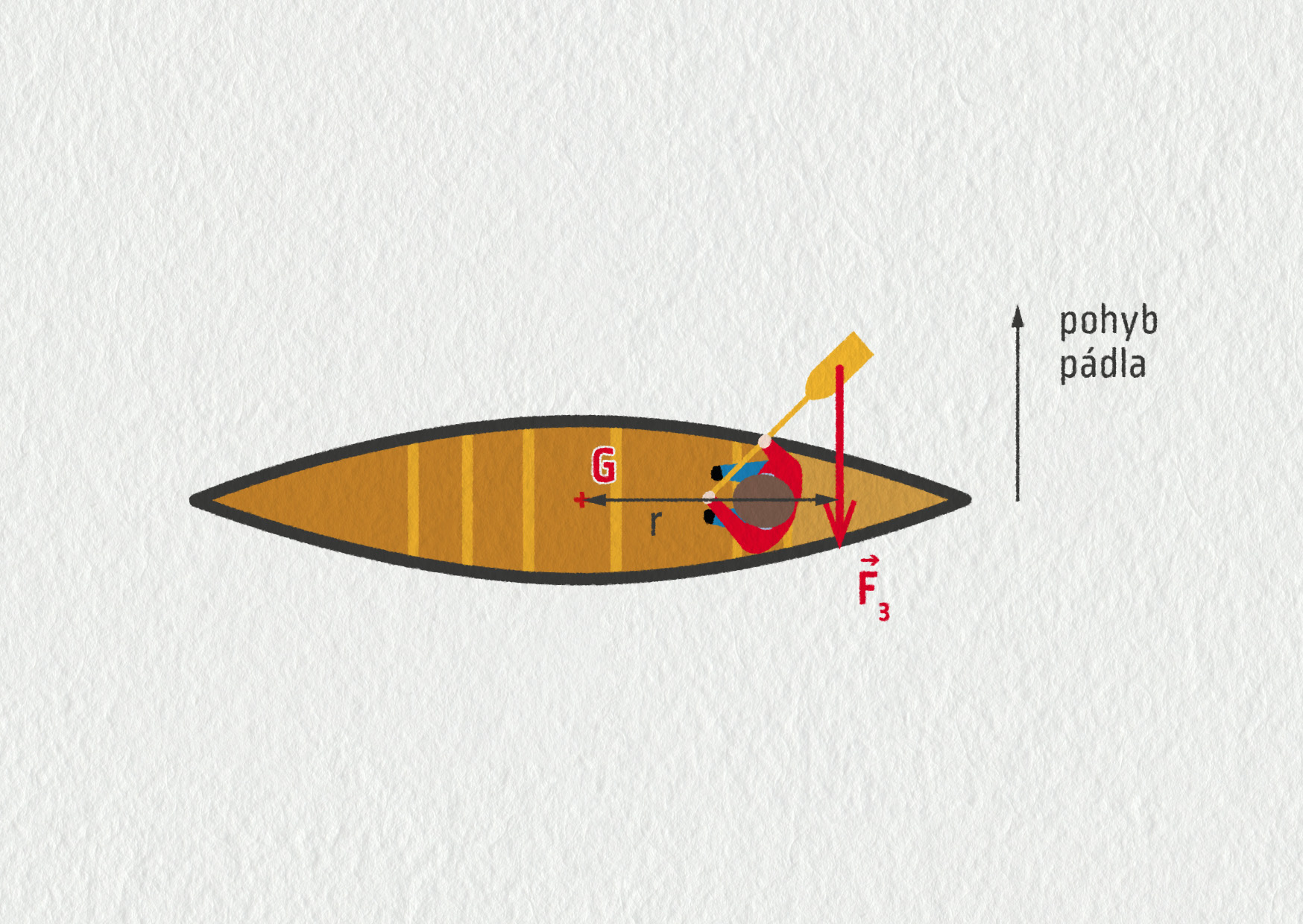
2) Kdyby zadák pádloval sám rovnoběžně s osou kánoe, loď by mu zatáčela doleva. Musí tedy pohyb korigovat. Zatlačí-li pádlem na vodu směrem od osy lodi, voda na jeho pádlo zapůsobí silou opačnou, a moment této síly vzhledem k těžišti otočí přídí doprava. Nyní už jen stačí oba pohyby „vyladit“, aby se otáčení vlevo a vpravo během jednoho záběru přesně vykompenzovalo.
Zdroj

