Souvislost mezi silovým působením a pohybem hmotného bodu, resp. translací vyjadřuje druhý Newtonův zákon \(\sum_i\Vec{F}_i=m\Vec{a}\): působící síly mohou měnit rychlost tělesa. Tytéž síly mohou za určitých podmínek těleso také roztočit. Podívejme se na vztah mezi silami a otáčivým pohybem podrobněji.
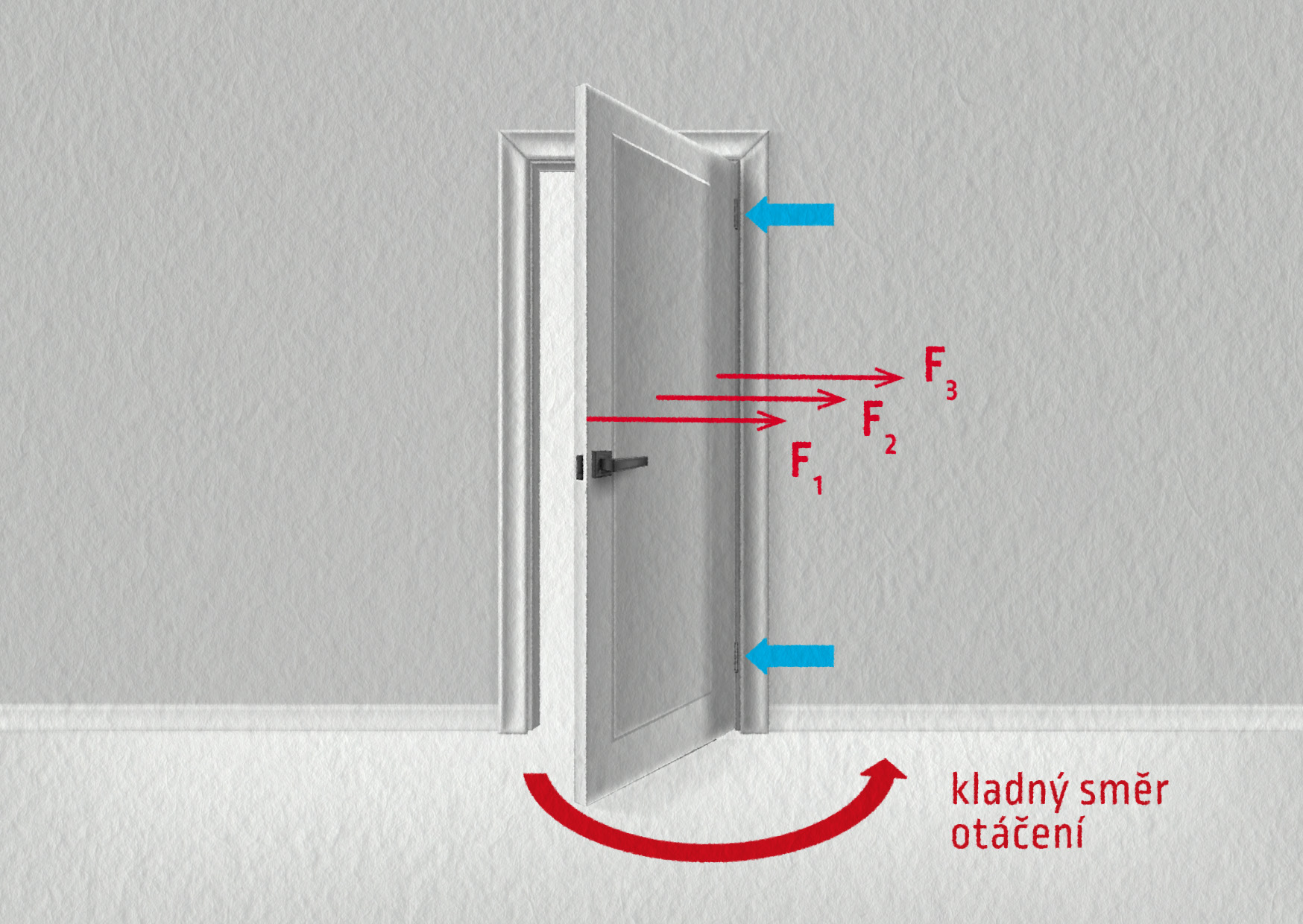
V situaci na obrázku 16.13 působí na dveře tři síly. Tyto síly sice mají stejnou velikost a stejný směr, ovšem každá z nich má jiný vliv na otáčení tělesa: síla \(\Vec{F}_1\), působící nejdál od svislé osy pantů, dveřmi otáčí nejvíce, naopak síla \(\Vec{F}_3\), působící přímo v ose otáčení, nemá žádný otáčivý účinek.
Zdroj
Z toho plyne, že síla samotná k pochopení a předvídání rotace nestačí a je třeba zohlednit i její polohu vůči ose otáčení. Proto definujeme veličinu moment síly, která dobře vystihuje schopnost těleso roztočit.
Definice momentu síly
\[ M_z = \pm rF \]\(M_z\) ... moment síly vzhledem k ose otáčení \(z\)
\(r\) ... rameno síly
\(F\) ... velikost síly
Moment síly je fyzikální veličina vyjadřující otáčivý účinek síly kolem dané osy. Konstruktéři automobilů jí říkají též „točivý moment“. Pokud chceme porovnávat účinky více sil na otáčení tělesa, musíme jejich momenty vždy vztahovat k téže ose – proto je praktické indexem vyznačit, o kterou osu se jedná, v našem případě osa \(z\), tedy \(M_z\).
Moment síly má jednotku newtonmetr N ⋅ m. Zapisujeme ji vždy jako N ⋅ m a nikdy jako m ⋅ N, aby nedošlo k záměně s milinewtony.
Jak jsme viděli v první motivační aktivitě, některé síly otáčí jedním směrem, jiné naopak – proto ještě než začneme momenty počítat, musíme si zvolit kladný směr otáčení. Je zvykem za kladný směr otáčení zvolit ten proti směru hodinových ručiček. Síla, která tělesem otáčí v kladném směru, bude mít kladný moment \(M_z\), síla otáčející v opačném směru pak záporný moment \(M_z\).
Rameno síly \(r\) je kolmá vzdálenost osy otáčení od přímky, na níž leží síla – viz obrázek 16.14.


Zdroj
Rameno síly je poněkud zrádný pojem, protože nemusí automaticky znamenat vzdálenost osy otáčení a působiště síly. Jak vidíte na dalším obrázku 16.15, tři stejné síly \(\Vec{F}_1\), \(\Vec{F}_2\) a \(\Vec{F}_3\) mají různá působiště. Ale poněvadž se nacházejí na jediné společné přímce, mají všechny stejné rameno r, a tím pádem i stejný otáčivý účinek: \(M_{z1}=M_{z2}=M_{z3}\).

Zdroj
Pokud přímka, na které síla leží, protíná osu otáčení \(z\), nemá tato síla na těleso žádný otáčivý účinek.
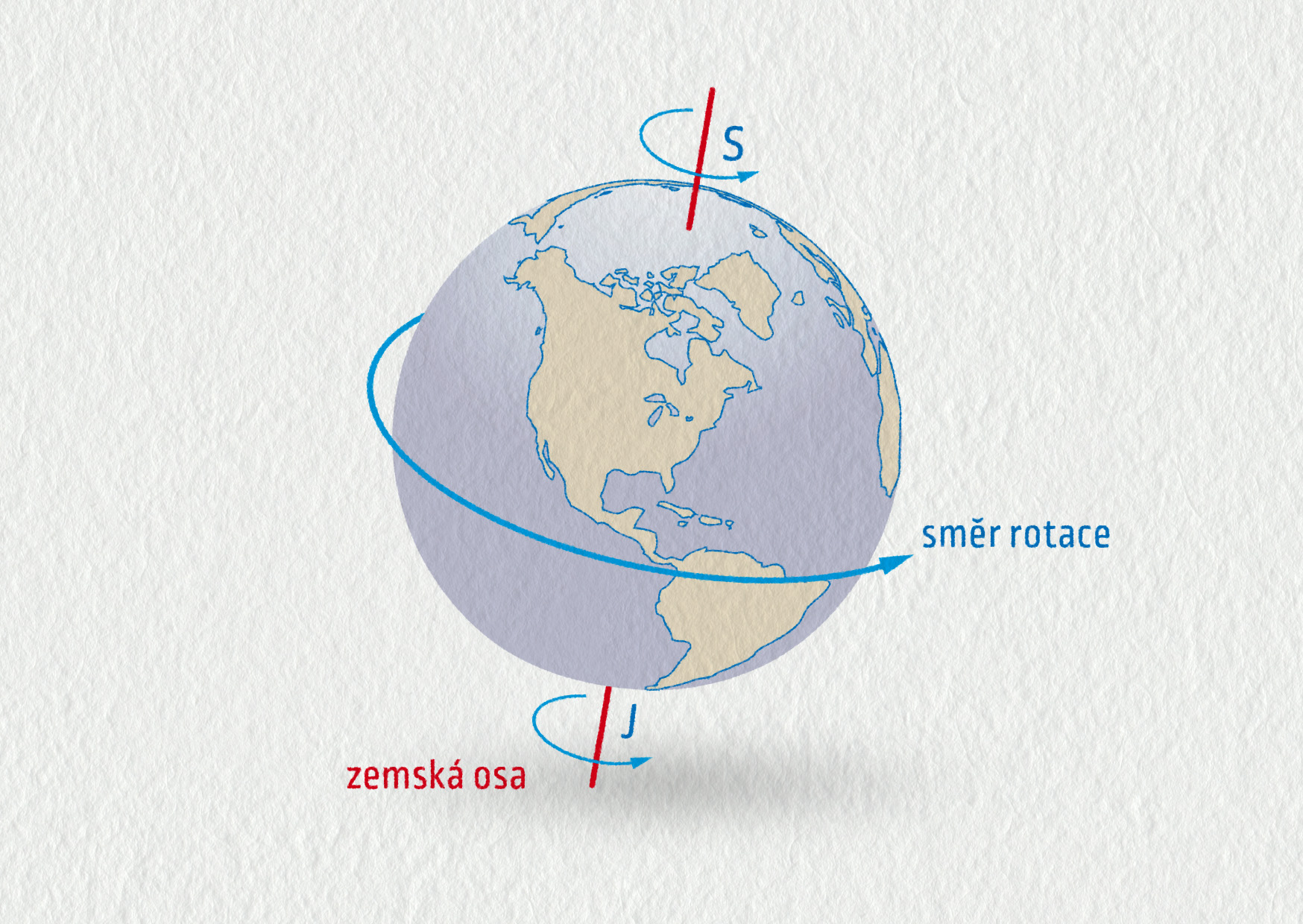
Moment síly jsme zavedli pro otáčení tělesa kolem pevné osy. Může se ovšem stát, že osa otáčení není v prostoru nijak „upevněna“. Například Země se otáčí vlastní setrvačností kolem osy procházející póly. Vliv Slunce, Měsíce a ostatních planet má za následek, že směr osy rotace Země se periodicky mění a do původního směru se osa vrátí za zhruba 26 000 let.
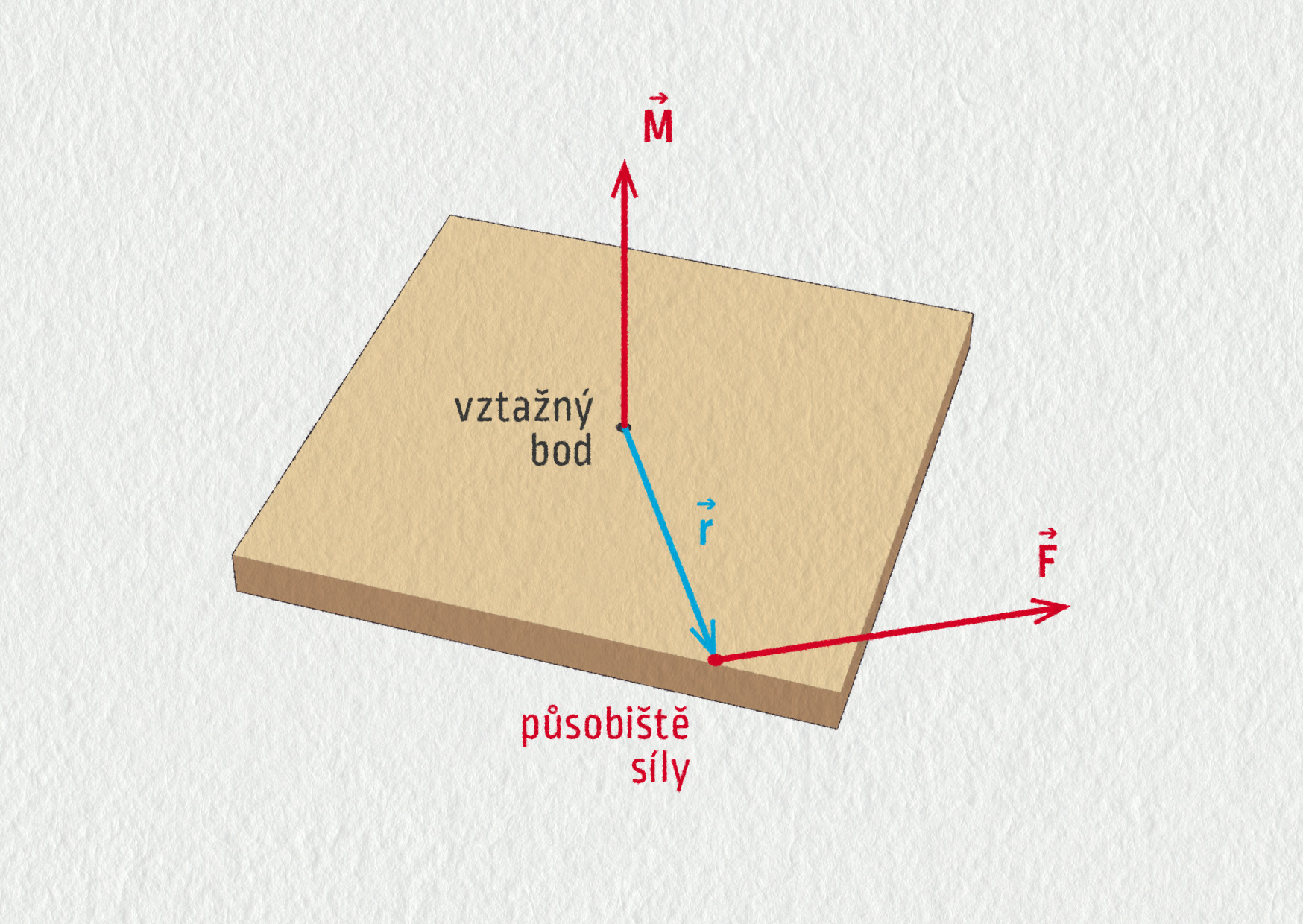
K popisu a pochopení těchto jevů je třeba zavést moment síly vzhledem k určitému bodu a definovat jej jako vektorovou veličinu. Moment síly se zavádí vztahem \(\Vec{M}_A=\Vec{r}\times\Vec{F}\), kde \(\Vec{M}_A\) je moment síly \(\Vec{F}\) vzhledem k bodu A a \(\Vec{r}\) vektor spojující bod A a působiště síly \(\Vec{F}\). Symbol × označuje vektorový součin dvou vektorů.
Zdroj
V případě rotace kolem pevné osy \(z\) má \(M_z\), zavedený ve výkladu, význam z-ové složky takto obecněji definovaného momentu \(\Vec{M}\).
Že se naše Země otáčí kolem svojí osy, vědí už žáci na základní škole. Ale proč se vlastně otáčí? A co ji pohání po miliony let?
Zdroj
Kdo pečlivě četl 5. kapitolu, už tuší, jak je to ve skutečnosti, a vidí, že předchozí otázka je poněkud zavádějící. V 5. kapitole jsme diskutovali o příčinách pohybu a zjistili jsme důležitou skutečnost: tělesa setrvávají v pohybovém stavu, v jakém byla na začátku pozorování, pokud se silové působení vyruší. Puk ležící na ledové ploše se sám od sebe nemůže dát do pohybu. Puk již klouzající po ledu má tendenci setrvávat ve svém rovnoměrném přímočarém pohybu, dokud nenarazí na hokejku, mantinel nebo dokud jeho pohyb nebude zbržděn třecí silou. Nepřekvapí nás tedy, že podobně to bude fungovat i při rotaci. Tělesa setrvávají v původním pohybovém stavu. Například hračka zvaná káča se sama od sebe nemůže roztočit a do pohybu se dá až díky působení síly ruky (s nenulovým momentem). A jakmile se již jednou pohybuje, točí se vlastní setrvačností tak dlouho, dokud ji moment třecí nebo jiné síly nezpomalí.

Zdroj
Podobně ani Země nepotřebuje ke svému otáčení žádný pohon, otáčí se miliardy let vlastní setrvačností a bude se i nadále otáčet, dokud ji vnější síly s nenulovým momentem nezpomalí! Tyto úvahy zobecňuje následující momentová věta.
Momentová věta
Těleso setrvává v klidu nebo se otáčí stálou úhlovou rychlostí, právě když je výsledný moment sil působících na toto těleso nulový.
\[\omega = \hbox{konst.}\quad\Leftrightarrow\quad \sum_i M_{zi} = 0 \]Momentová věta je analogií prvního Newtonova zákona pro otáčivý pohyb. Pokud se těleso neotáčí, je jeho úhlová rychlost nulová (\(\omega=0=\hbox{konst.}\)).
Velmi často na vybrané těleso působí více sil současně a každá může mít na těleso jiný otáčivý účinek. Výsledný moment získáme sečtením momentů jednotlivých sil
\[ \sum_i M_{zi} = M_{z1} + M_{z2} + M_{z3} + \dots, \]musíme ovšem vztahovat všechny momenty k téže ose \(z\) a respektovat znaménka jednotlivých momentů podle naší volby kladného směru otáčení.
Podmínka, že je výsledný moment nulový, znamená, že se momenty působících sil vzájemně vyruší. Jinými slovy, součet momentů sil otáčejících tělesem v kladném směru je stejně velký jako součet momentů sil otáčejících tělesem v záporném směru.
Momentová věta platí pro otáčení kolem osy, která v inerciální vztažné soustavě nemění svůj směr.
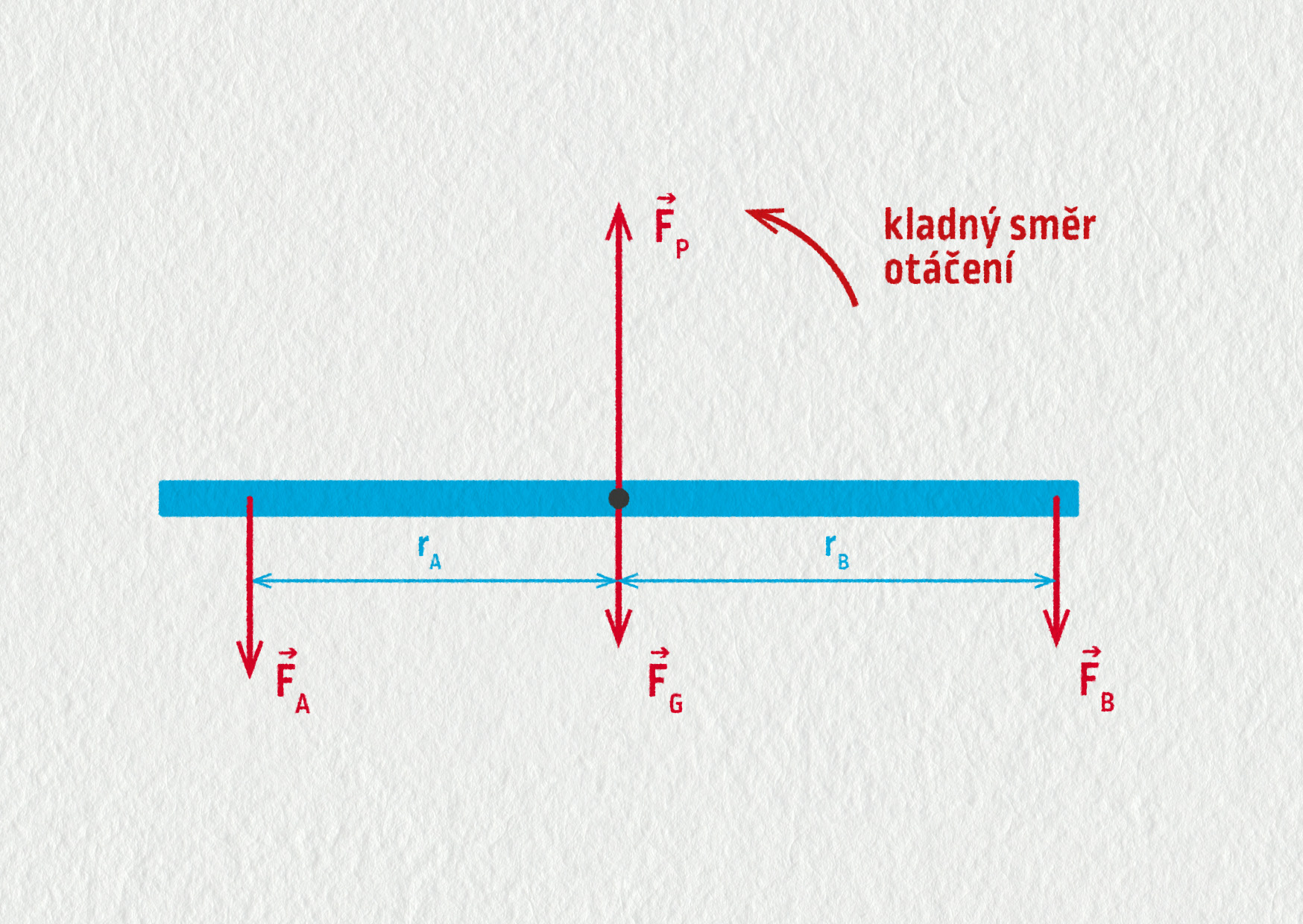
Houpačka je tvořena trámkem o hmotnosti 15 kg, který se může volně otáčet kolem svého těžiště – viz obrázek 16.20. Adélka působí na trámek silou 170 N vlevo ve vzdálenosti 1,1 m od osy otáčení, Bára silou 130 N vpravo ve vzdálenosti 1,4 m od osy otáčení. Za kladný směr otáčení zvolíme ten prosti směru chodu hodinových ručiček.
Určete síly působící na trámek a jejich momenty vzhledem k ose otáčení houpačky. Bude houpačka setrvávat v rovnováze?

Zdroj
Na trámek působí čtyři svislé síly:
- tlaková síla vyvolaná Adélkou FA = 170 N směrem dolů,
- tlaková síla vyvolaná Bárou FB = 130 N směrem dolů,
- tíhová síla trámku FG = 150 N směrem dolů,
- tlaková síla vyvolaná podpěrou (osou) FP směrem vzhůru.
Těžiště trámku se nepohybuje, proto se podle prvního Newtonova zákona musí působící síly vyrušit: FP = FA + FB + FG = 450 N.
Zdroj
Momenty sil vzhledem k těžišti určíme z definice \( M_z = \pm rF \):
- MzA = + 187 Nm,
- MzB = – 182 Nm,
- MzG = 0 Nm,
- MzP = 0 Nm.
Součet momentů působících sil je +5 Nm. Třebaže se síly vzájemně vyruší, jejich momenty nikoli. Houpačka není v rovnováze, má tendenci se otáčet směrem k Adélce.
Pokud se momenty nevyruší, úhlová rychlost otáčení tělesa kolem pevné osy se bude měnit, takže rotace tělesa se bude zrychlovat, nebo zpomalovat. V tomto případě má smysl definovat úhlové zrychlení \(\varepsilon=\Delta\omega/\Delta t\) jakožto změnu úhlové rychlosti za časovou jednotku. Potom platí
\[ \sum_i M_{zi}=J\varepsilon\;, \]kde konstanta \(J\) se nazývá moment setrvačnosti a charakterizuje rozložení hmoty kolem osy otáčení \(z\). O momentu setrvačnosti se dočtete více v podkapitole 16.5 věnované rotační kinetické energii.

