Nyní máme již vše připraveno ke zformulování podmínek statické rovnováhy. Tyto podmínky jsou ve stavebnictví základním principem, jehož splnění rozhoduje o tom, zda se budova zřítí, či nikoli.
Statickou rovnováhou rozumíme stav, kdy těleso setrvává v klidu:
- neprobíhá translace, těžiště tělesa se neposouvá: \(v=0 \) m/s
- neprobíhá rotace, těleso se neotáčí kolem žádné osy: \(\omega=0 \) rad/s
K tomu, aby těžiště setrvávalo v klidu, musí se působící síly vzájemně vyrušit. K tomu, aby se těleso neroztočilo, musí se navíc přesně vykompenzovat momenty těchto sil. Zapamatujme si:
Podmínky statické rovnováhy
Rovnováha sil: \(\sum_i \Vec{F}_i = \Vec{0}\)
Rovnováha momentů: \(\sum_i M_{zi} = 0\)
Ve výrazu
\[ \sum_i \Vec{F}_i = \Vec{F}_1 + \Vec{F}_2 + \Vec{F}_3 + \dots \]sčítáme vektorově všechny síly, kterými okolí působí na studované těleso.
Jelikož se těleso v rovnováze nesmí otáčet vůči žádné ose, můžeme si při řešení příkladů polohu osy zvolit co nejjednodušeji. Všechny momenty ve výrazu
\[ \sum_i M_{zi} = M_{z1} + M_{z2} + M_{z3} + \dots \]musíme poté vztahovat k této jediné zvolené ose.
Dva hasiči drží žebřík o délce 6,0 m a hmotnosti 36 kg s těžištěm přesně uprostřed. První hasič podpírá žebřík 1,0 m od jednoho konce, druhý hasič ve vzdálenosti 0,5 m od opačného konce. Vypočítejte síly, kterými hasiči na žebřík působí.
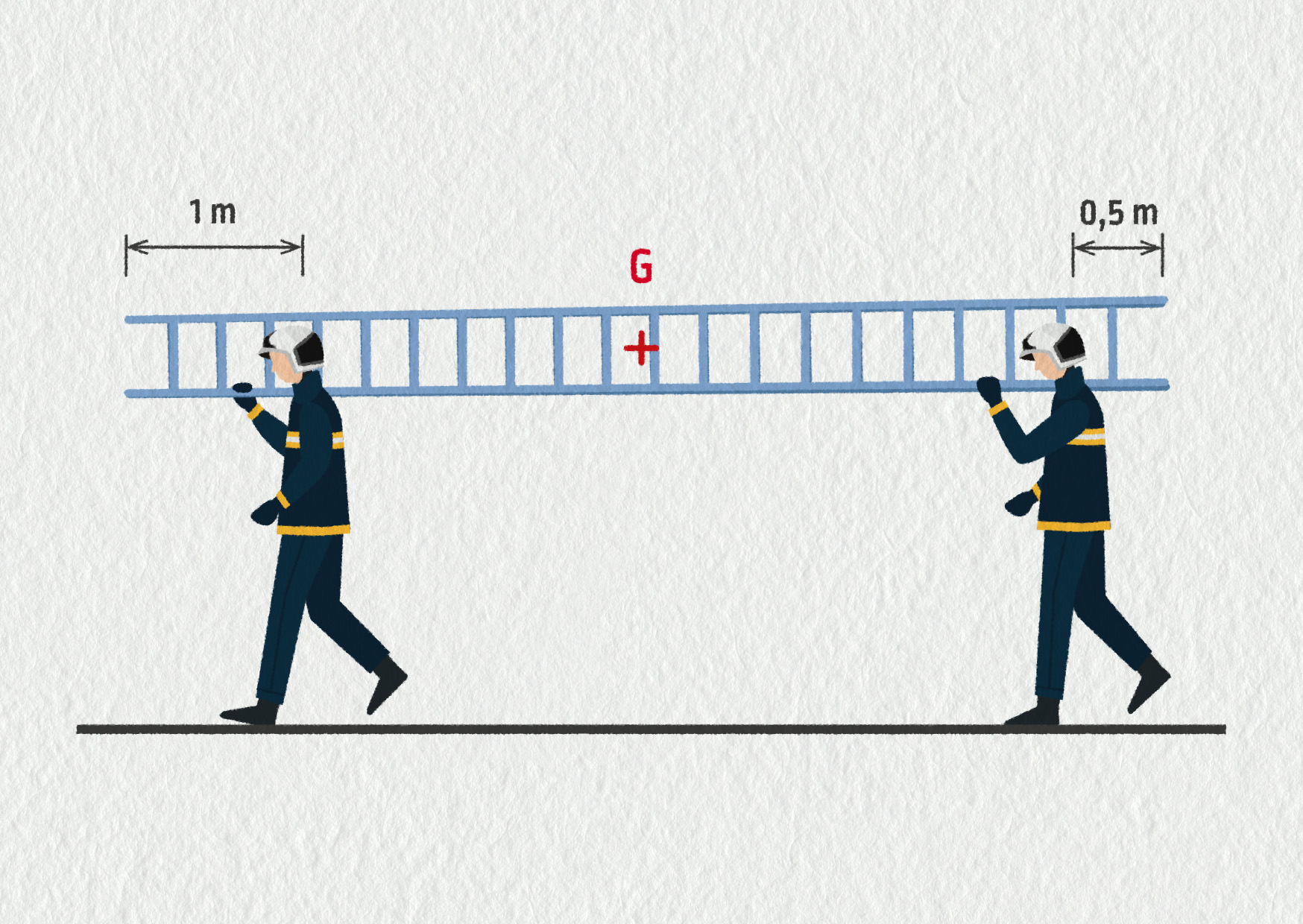
Zdroj
Řešení začneme tradičně obrázkem, do kterého si vyznačíme síly působící na žebřík. Jsou to gravitační síla \(\Vec{F}_\mathrm{G}\) působící v těžišti a dvě tlakové \(\Vec{F}_1\) a \(\Vec{F}_2\), jimiž hasiči žebřík podpírají.
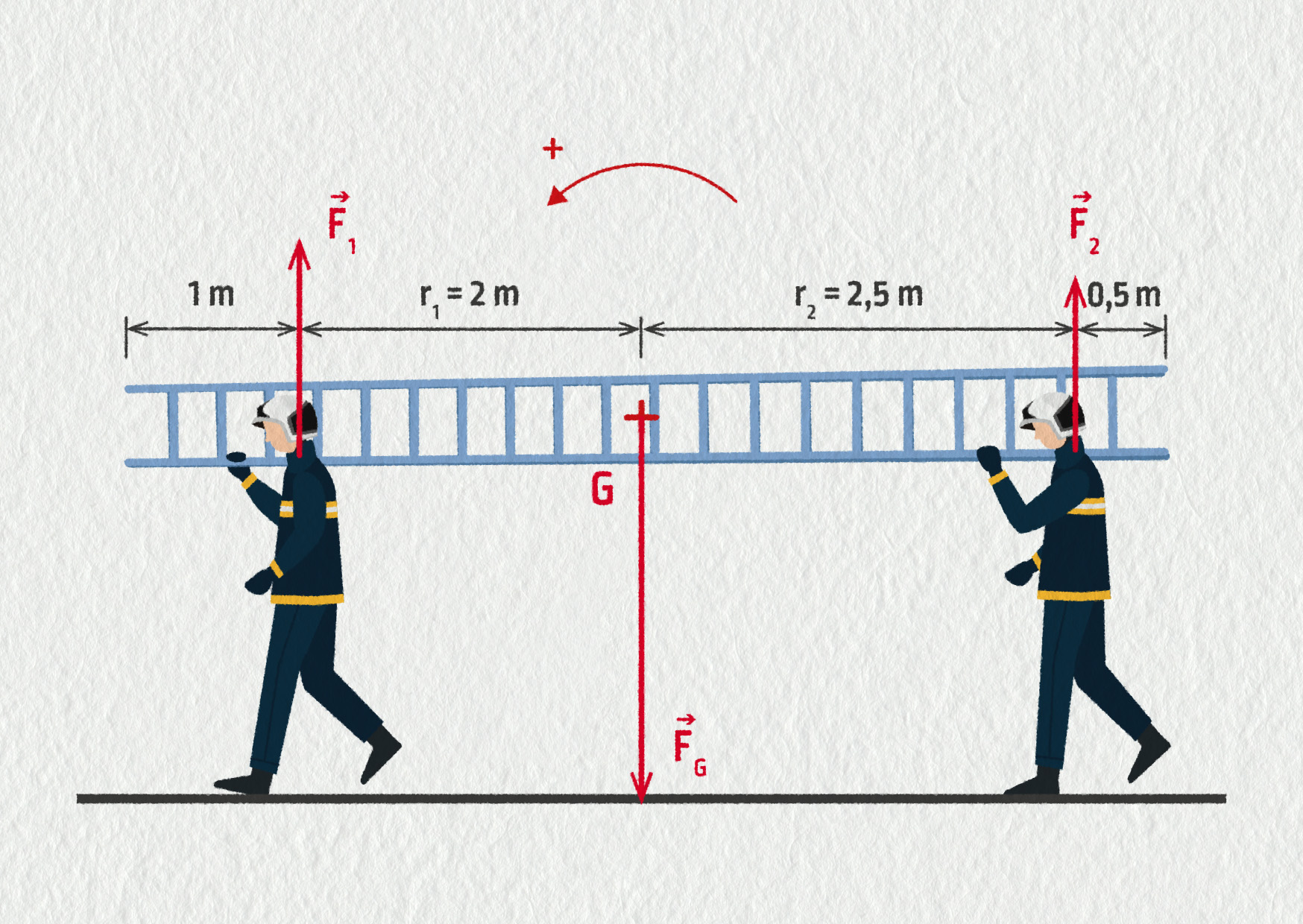
Zdroj
Počítáme dvě neznámé síly, potřebujeme tedy sestavit dvě rovnice.
Těžiště žebříku setrvává v klidu, takže se síly musí vzájemně vyrušit \(\Vec{F}_\mathrm{G}+\Vec{F}_1+\Vec{F}_2=\Vec{0}\). Síly působící směrem vzhůru musí přesně kompenzovat gravitační sílu. Pro jejich velikosti platí \(F_1+F_2=F_\mathrm{G}\).
Žebřík se neotáčí vůči žádné ose, nesmí se tedy otáčet ani vůči vodorovné ose procházející těžištěm G, kolmé k rovině nákresu. Zvolíme kladný směr otáčení vyznačený v obrázku 16.31. Moment síly \(F_1\) je \(M_1=-r_1F_1\), moment síly \(F_2\) je \(M_2=+r_2F_2\), moment gravitační síly \(F_\mathrm{G}\) je \(M_\mathrm{G}= 0\cdot F_\mathrm{G}=0\). Dosadíme do podmínky rovnováhy momentů \(M_1+M_2+M_\mathrm{G}=-r_1F_1+r_2F2+0=0\) čili \(r_1F_1=r_2F_2\).
Rovnováha sil \(F_1+F_2=F_\mathrm{G}\) a rovnováha momentů \(r_1F_1=r_2F_2\) představuje soustavu dvou rovnic pro dvě neznámé \(F_1\) a \(F_2\). Pokud byste si netroufli na obecné řešení, můžete soustavu vyřešit s dosazenými číselnými hodnotami. Vezmeme \(m=36\ \mathrm{kg}\), takže \(F_\mathrm{G}=360\ \mathrm{N}\), z obrázku určíme délku ramen \(r_1=2\ \mathrm{m}\), \(r_2=2{,}5\ \mathrm{m}\), takže soustava přechází do tvaru
\[ \begin{aligned} F_1+F_2&=360\\ 2F_1&=2{,}5F_2\\ \end{aligned} \](Fyzikální vztahy mají tu hezkou vlastnost, že když budete systematicky dosazovat v základních jednotkách SI, bude výsledek vždy vyjádřen v SI.)
Řešením soustavy jsou síly \(F_1=200\ \mathrm{N}\) a \(F_2=160\ \mathrm{N}\).
Podobným způsobem bychom mohli počítat, jakými silami podpírají pilíře hlavní nosnou konstrukci mostu, jakými silami podpírají svislé stěny stropní desku atp.
Poznámka: Úlohu si můžete spočítat i vůči ose procházející některou z podpěr – výsledek vyjde stejně.
Rovnovážné polohy těles můžeme podle polohy těžiště rozdělit do tří kategorií.
Ve stálé (stabilní) rovnovážné poloze se nachází těžiště tělesa nejníže. Těleso má v rovnovážné poloze minimální potenciální energii a po malém vychýlení se do této polohy samovolně vrací.
Opakem je vratká (labilní) rovnovážná poloha. Těžiště tělesa je nejvýše, jeho potenciální energie má v rovnovážné poloze maximum a po malém vychýlení se těleso z rovnovážné polohy samovolně vzdaluje.
Existuje ještě volná (indiferentní) rovnovážná poloha, v níž je výška těžiště, potažmo potenciální energie tělesa stálá. Po malém vychýlení je i v nové pozici těleso v rovnováze.
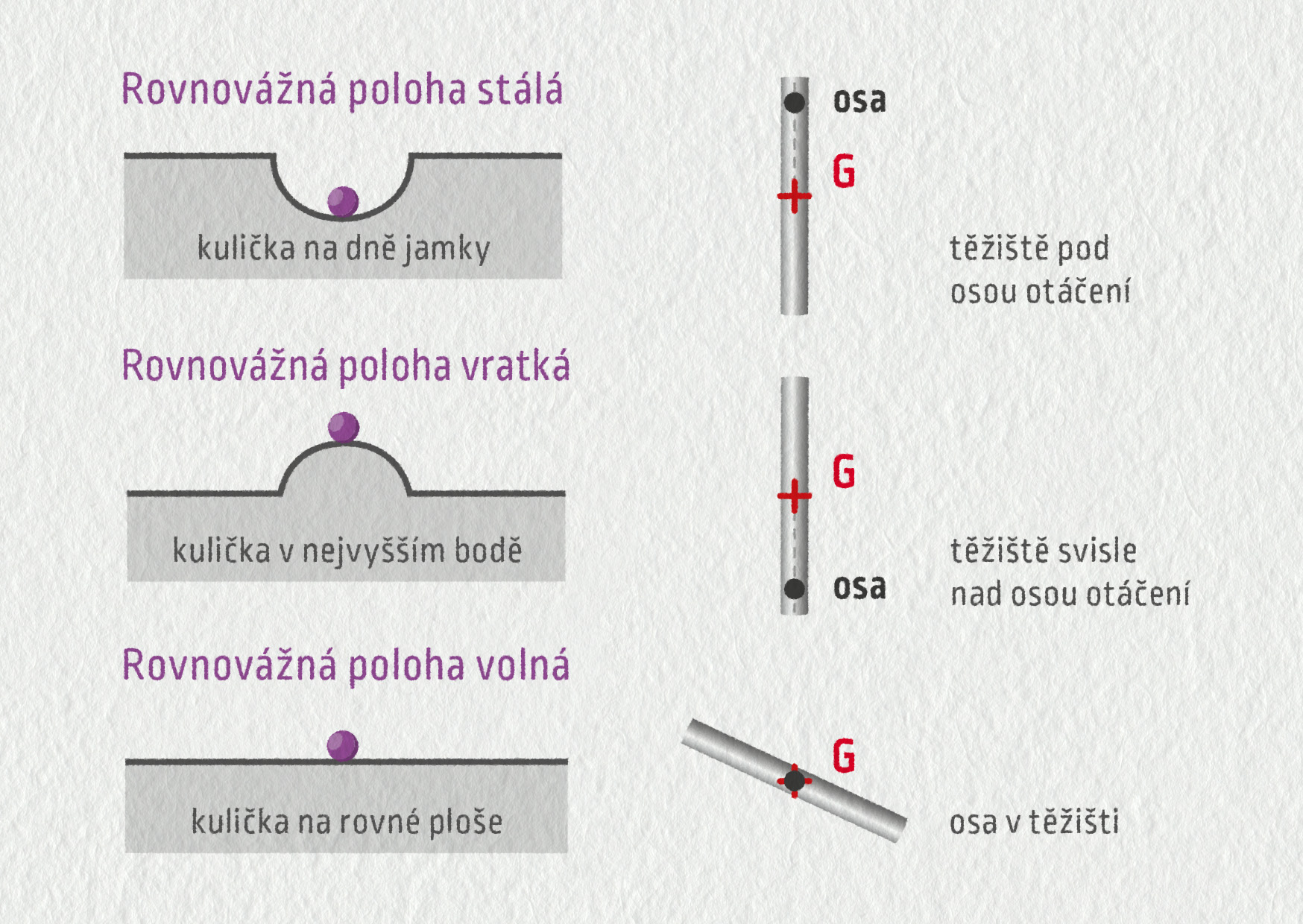
Zdroj
Rovnovážné polohy

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

