Síly kolem nás

Pojďme se podívat kolem sebe a prozkoumat, s jakými silami se setkáme nejčastěji. Poznejme síly, které slouží k popisu pohybu lidí, aut či vodních kapek. Zatím vynechejme síly elektrické, magnetické nebo jaderné.

Všichni jsme si již všimli účinků tíhové síly; to je síla, která nás přitahuje k Zemi. Když ale plaveme v bazénu, cítíme se „lehčí“, protože na nás působí další výrazná síla, která nás nadlehčuje – síla vztlaková. Když se chceme rozejít nebo třeba jedeme na kole, působí na nás další síly: díky třecí síle se „odrazíme“ vpřed a rozejdeme nebo rozjedeme se. S rostoucí rychlostí nás ale bude brzdit čím dál větší odporová síla vzduchu. Jaké mají tyto síly vlastnosti?

Podívejme se na ně podrobněji.

Tíhová síla

Když si stoupnete na osobní váhu, váha vám sice ukáže vaši hmotnost, ale ve skutečnosti měří velikosti síly, kterou na ni tlačíte. A takto velkou silou – tíhovou silou \(\Vec{F}_\mathrm{G}\) – vás k sobě přitahuje Země. Tíhová síla je síla působící na těleso o hmotnosti m na povrchu Země a v její blízkosti.

Konstanta g, kterou násobíme hmotnost, se nazývá tíhové zrychlení a v České republice přibližně platí g = 9,8 N/kg. Přesnější hodnotu pro dané místo na povrchu Země lze najít na internetu.

Provedete-li stejné vážení na povrchu Měsíce, dostanete nižší hodnotu, přestože vaše hmotnost zůstává stejná (nebo spíše bude větší kvůli hmotnosti skafandru). Měsíc vás bude přitahovat menší silou a váha ukáže menší hodnotu než na Zemi.

Poznámka na okraj: Určování vodorovného a svislého směru v praxi (olovnice, vodováha)

Od nepaměti, kdy se člověk snažil pro sebe vybudovat nějaké přístřeší, musel řešit, jak stavbu postavit, aby byla dostatečně stabilní. Postupně se naučil rozlišovat dva základní směry – svislý a vodorovný. Vodorovný směr je směr rovnoběžný s klidnou vodní hladinou. Ve stavebnictví, ale i jinde, ho určujeme pomocí vodováhy. Její princip je jednoduchý: dlouhá (obvykle hliníková) tyč s vloženou trubicí s bublinkou obklopenou kapalinou – pokud je vzduchová bublinka mezi kalibrovanými čárkami, je tyč položena vodorovně.

Svislý směr zase nejčastěji určujeme pomocí olovnice. Není to nic jiného než provázek, na jehož konec připevníme závaží. Jakmile ho spustíte dolů, ukáže vám směr svislý, tedy např. rovnost postavené zdi a pro nás fyziky směr tíhové síly.

Jak tíhovou sílu zakreslujeme? Pomocí orientované úsečky, která směřuje dolů, má počátek v těžišti tělesa a jejíž délka znázorňuje velikost této síly v určitém měřítku (viz obrázek). Například u kettlebelu na obrázku, jehož hmotnost je 12,0 kg, je velikost tíhové síly rovna F_G = mg = 12,0 kg ⋅ 9,8 N/kg = 118 N. Tuto sílu v daném měřítku zakreslíme vektorem o délce 11,8 cm.

Celkově tedy můžeme zapsat \(\Vec{F}_\mathrm{G}=m\Vec{g}\). Vektor tíhového zrychlení \(\Vec{g}\) je totožný se zrychlením padajících těles (rovnoběžně s olovnicí). Více se o padajících tělesech dozvíme v kapitole 15.

Kolmá tlaková síla

V úvodu této kapitoly jsme viděli situaci, kdy ruka boxera naráží do boxovacího pytle a ten se pod úderem deformuje. Pytel a ruka boxera na sebe vzájemně působí silami. Této síle, která se objevuje vždy, když se nějaká tělesa dotknou, říkáme kolmá tlaková síla.

V případě kulečníkové koule ležící na stole na sebe vzájemně působí stůl a koule kolmými tlakovými silami. Kromě tlakové síly působí na kouli ještě tíhová síla, tyto síly se navzájem vyruší, a proto koule nepropadne podložkou.

Kolmá tlaková síla \(\Vec{F}_\mathrm{N}\), zvaná též normálová síla, se objevuje vždy při vzájemném dotyku těles. Jaké jsou její vlastnosti?

Poznámka: Velikost tlakové síly závisí na dalších působících silách a zrychlení tělesa, naučíme se ji počítat v následující kapitole. Tlaková síla ale nemůže být libovolná, její maximum je dáno pevností těles.

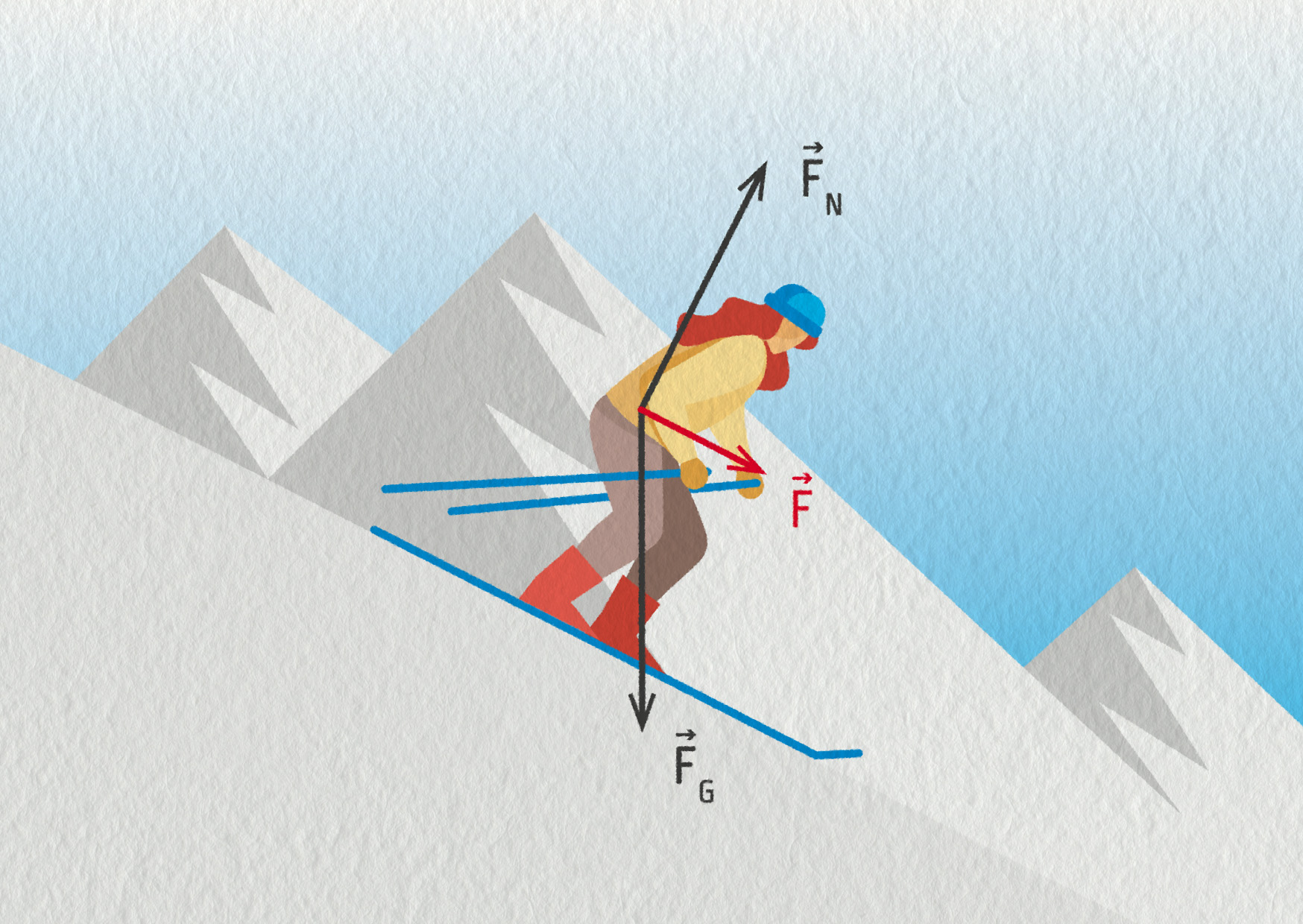
Kolmá tlaková síla působí bez ohledu na to, jestli jsou tělesa v klidu nebo v pohybu. Podívejme se na příklad lyžaře, který sjíždí ze svahu. Tíhová síla \(\Vec{F}_\mathrm{G}\) působí svisle dolů, ale tlaková síla podložky \(\Vec{F}_\mathrm{N}\) je kolmá ke svahu. Ostatní síly zanedbáváme.

Jejich vektorovým součtem získáme výslednou sílu \(\Vec{F}_\mathrm{G}+\Vec{F}_\mathrm{N}=\Vec{F}\), která je rovnoběžná se svahem, a díky ní lyžař zrychluje.

Velikost kolmé tlakové síly závisí na konkrétní situaci. V případě lyžaře na svahu bude mít menší hodnotu, než když lyžař stojí dole pod svahem (viz obrázek).

Poznámka na okraj: Jak na sebe působí dvě tělesa, která se dotýkají?

Síly mezi atomy mohou být přitažlivé i odpudivé, záleží na jejich vzdálenosti. To vysvětluje soudržnost pevných látek. Tlaková síla vzniká přiblížením atomů.

Už jste někdy přemýšleli, proč nemůžete projít zavřenými dveřmi? Co se asi děje na atomární úrovni? Atomy vašeho těla se přiblíží tak blízko k atomům dveří, že se začnou odpuzovat elektrickou silou (viz obrázek 4.32 níže). Atomy jsou k sobě stále blíž a blíž, síla narůstá… Dveře i vaše tělo se začínají deformovat! Dveře jsou však dostatečně pevné, a proto nedojde při deformaci k porušení jejich struktury. Atomy dveří i vašeho těla zůstávají vždy v takové vzdálenosti, že jejich odpuzování vyvolá tlakovou sílu potřebné velikosti.

Třecí síla

Třecí síla \(\Vec{F}_\mathrm{t}\) je síla, která působí při styku dvou pevných těles. Díky tření nekloužou věci samovolně ze svahu dolů, tření nás brzdí při jízdě na lyžích. Bez tření bychom nemohli chodit ani jezdit autem, protože kola by se protáčela a boty klouzaly jako na ledě.

Proč tomu tak je? Proč je těžké posunout skříň po podlaze? Skříň se dotýká podlahy, podlaha a skříň na sebe vzájemně působí tlakovými silami, atomy jsou velmi blízko a odpuzují se (viz graf interakce Ar-Ar). Jakmile ale zatlačíte ve vodorovném směru, objeví se nová síla, která působí proti vám. Je to třecí síla a je způsobena mikroskopickými nerovnostmi mezi dvěma povrchy (viz obrázek povrchu lesklé lžičky).

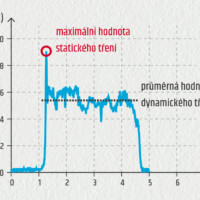
Pokud se vám podaří se skříní pohnout, začnou se navíc mikroskopické kousky povrchů odlamovat a ulpívají na druhém povrchu: dochází k opotřebení materiálu. Třecí síla působí vždy v rovině styčné plochy těles. Může působit jak v klidu (klidové, statické tření), tak při pohybu dotýkajících se těles (smykové, dynamické tření). Má následující vlastnosti:

F_N je velikost kolmé tlakové síly, která působí na těleso, a koeficient f_D či f_S je dynamický nebo statický koeficient tření, který závisí hlavně na druhu materiálu a vlastnostech povrchů tělesa a podložky, a obvykle nezávisí na velikosti styčné plochy.

U statického tření máme vzorec pro maximální hodnotu síly, po jejímž překročení se těleso dává do pohybu. Dynamické tření, které následuje po uvedení tělesa do pohybu, je menší než maximální statické.

Konkrétní hodnoty koeficientů tření najdete v následující tabulce.

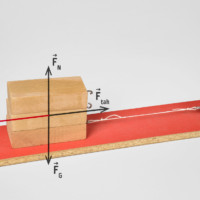
Jak můžeme zkoumat velikost třecí síly?

Někdy se tření snažíme snížit tím, že povrchy od sebe oddálíme pomocí tenké vrstvy vzduchu, vody nebo oleje. Proto auto na mokré silnici hůř brzdí, proto mažeme ložiska, dveřní závěsy či motory olejem. A oddělit od sebe pohybující se tělesa vzduchem? Proč ne? Sami si můžete zkusit vyrobit jednoduché vznášedlo.

V technické praxi se na vzduchovém polštáři přesunují i velmi těžké objekty, jako například části detektoru ALICE v CERNu. Jindy naopak chceme, aby třecí síla byla velká a my jsme s její pomocí bezpečně zastavili auto nebo kolo.

Kde se setkáme se třením?

Příklad 1

Příklad: Na stole leží kniha o hmotnosti 0,80 kg. Abyste ji posunuli, musíte na ni tlačit silou o velikosti 2,25 N. Když se již pohybuje konstantní rychlostí, stačí na ni tlačit silou o velikosti pouze 1,50 N. Jaké jsou hodnoty koeficientů statického a dynamického tření mezi knihou a stolem?

Řešení:

Protože je hmotnost knihy 0,80 kg a kniha leží na vodorovném stole, je kolmá tlaková síla rovna 7,84 N. Velikost statické třecí síly je vyjádřena vztahem \(F_\mathrm{t}=f_\mathrm{S}F_\mathrm{N}\). Pro koeficient statického tření tak dostáváme \[ f_\mathrm{S}=\frac{F_\mathrm{t}}{F_\mathrm{N}}=\frac{2{,}25}{7{,}84}=0{,}29 \] Obdobně pro koeficient dynamického tření dostáváme \(f_\mathrm{D}=0{,}19\).

Kontrolní otázka

Představte si lyžaře, který stojí na svahu na obou lyžích. Jak se změní třecí síla v případě, že zvedne jednu nohu a zůstane stát pouze na jedné lyži?

Bude větší
Bude menší
Zůstane stejná

Odeslat  

Třecí síla podle vzorce F_tS = f_S·F_N nezávisí na velikosti styčné plochy, ale pouze na kolmé tlakové síle a koeficientu tření. Tyto veličiny se však nezměnily. Hmotnost lyžaře se nezměnila, tudíž zůstává stejná i síla, kterou lyžař tlačí do podložky. V případě pohybu může být výhodnější jet po jedné lyži, protože nyní nejde čistě o tření, ale do hry vstupuje i deformace sněhu.

Kontrolní otázka

Vozy formule 1 mají tzv. přítlačné plochy, které vytvářejí aerodynamickou sílu působící směrem dolů. K čemu tyto části karoserie závodních vozů slouží?

ke snížení aerodynamického odporu vozu a dosažení větší rychlosti,
ke zvýšení třecí síly mezi pneumatikami a povrchem vozovky,
ke snížení třecí síly mezi pneumatikami a povrchem vozovky,
na okrasu a zvětšení reklamních ploch.

Odeslat  

Vzduch, který je obtéká, vytváří sílu směrem dolů, a zvyšuje tím tlakovou sílu F_N mezi silnicí a formulí. Díky většímu tření pak může formule lépe zrychlovat, zatáčet i brzdit.

Kontrolní otázka

Jakou maximální třecí sílu může vyvinout formule?

sílu o velikosti tíhové síly formule
sílu rovnou kolmé tlakové síle působící na vůz
sílu závisející na kolmé tlakové síle formule a koeficientu statického tření
sílu závisející na kolmé tlakové síle formule a koeficientu dynamického tření
libovolnou sílu

Odeslat  

Viz vzorec pro velikost třecí síly.

Kontrolní otázka

O jakém druhu tření se bavíme v případě otáčejícího se kola jedoucí formule? A proč?

statické tření, protože kolo nesmí proklouznout
dynamické tření, protože formule jede
statické tření i dynamické tření, protože formule jede a ani nesmí proklouznout

Odeslat  

Více o tření v dopravě se můžete dozvědět v rozšiřujícím článku Tření v dopravě.

Najdeme příklady, kdy využijeme velikou třecí sílu, a dokonce se ji ještě snažíme zvýšit jako v případě formule 1.

U kolových dopravních prostředků je situace o něco složitější. Díky tření mezi kolem a zemí se mohou rozjíždět, brzdit a zatáčet. Na valící se kolo ale zároveň působí ještě další síla – síla valivého odporu. Ten působí proti směru pohybu a je způsoben deformací kola a podložky. Pro dopravní prostředky tedy požadujeme co největší tření a zároveň co nejmenší valivý odpor.

Více o tření v dopravě se můžete dozvědět v rozšiřujícím článku Tření v dopravě.

Vztlaková síla

Vztlaková síla \(\Vec{F}_\mathrm{VZ}\) působí na každé těleso ponořené do kapaliny nebo plynu (souhrnně: tekutiny). Když plaveme ve vodě, voda nás nadlehčuje a my se bez většího úsilí udržíme s hlavou nad vodou. V případě koupání v Mrtvém moři (Izrael) se nad hladinou vody nachází tak velká část těla, že si klidně při „plování na vodě“ můžete číst noviny.

Jak je to možné? Na čem závisí síla, která nás nadlehčuje – vztlaková síla?

Provedete-li experimenty popisované v laboratorním cvičení, snadno objevíte vlastnosti vztlakové síly. Pro její velikost platí vztah \(F_\mathrm{VZ} = \varrho_\mathrm{k}Vg\), kde ϱ_k je hustota kapaliny (tekutiny), V je objem ponořené části tělesa a g je tíhové zrychlení. Vztlaková síla těleso nadlehčuje, působí proti gravitaci, můžeme tedy říci, že má směr svislý a je orientována vzhůru. Její působiště zakreslíme do geometrického středu ponořené části tělesa.

Poznámka na okraj: Původ vztlakové síly

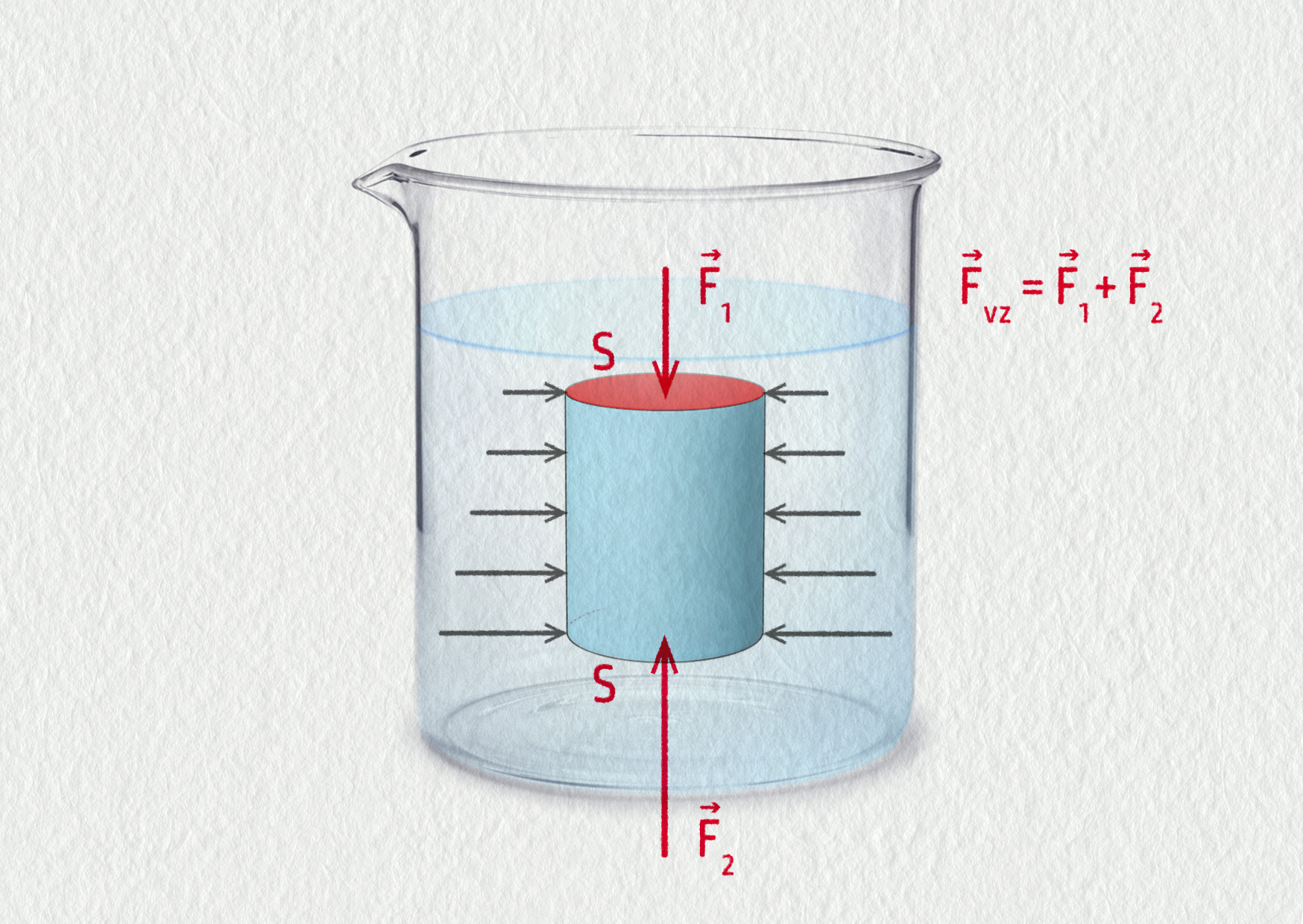
Její původ spočívá v tlakovém působení okolní tekutiny na těleso. V gravitačním poli se s hloubkou zvyšuje tlak (hydrostatický tlak, \(p_\mathrm{h}=h\varrho g\), znáte ze ZŠ). Proto na spodní části tělesa působí větší tlakové síly než na horní. Vztlaková síla je dána rozdílem tlakových sil působících v různých hloubkách

\[ \begin{aligned} F_\mathrm{VZ}&=F_2-F_1\\ F_\mathrm{VZ}&=p_{\mathrm{h}2} S-p_{\mathrm{h}1} S\\ F_\mathrm{VZ}&=S(h_2 \varrho g-h_1 \varrho g)\\ F_\mathrm{VZ}&=S(h_2-h_1)\varrho g \end{aligned} \]

Pokud si uvědomíme, že rozdíl hloubek je vlastně výška tělesa a součin výšky a obsahu podstavy je roven objemu V tělesa, máme před sebou konečný vztah pro výpočet velikosti vztlakové síly.

\(F_\mathrm{VZ}=V\varrho g\)

Představíme-li si kapalinu ve stavu beztíže, žádný význačný směr znamenající hloubku tam nenajdeme a vztlaková síla tam působit nebude.

Příklad 2

Vypočítejte velikost vztlakové síly, která působí na člověka o objemu 75 dm³ a hmotnosti 73 kg, který je zcela ponořený v čisté vodě. Jak se změní velikost této síly, jestliže se člověk ponoří do mořské vody o hustotě 1030 kg/m³? Porovnejte vztlakovou sílu s tíhovou silou.

Řešení:

Vztlakovou sílu spočítáme podle vzorce \(F_\mathrm{VZ}=V\varrho g\). V případě, že je člověk zcela ponořen, můžeme přímo dosadit:

čistá voda F_VZ = 0,075 m³ ⋅ 1000 kg/m³ ⋅ 9,8 N/kg = 735 N

mořská voda F_VZ = 0,075 m³ ⋅ 1030 kg/m³ ⋅ 9,8 N/kg = 757 N

Tíhová síla je stále stejná F_G = mg = 73 kg ⋅ 9,8 N/kg = 715 N

Objem lidského těla se při dýchání mění. Když se v čisté vodě nadechnete, stoupáte k hladině, pokud vydechnete, klesáte ke dnu. Jak je to s člověkem v tomto příkladu?

Příklad 3

Borový kmen o hmotnosti 120 kg a hustotě 850 kg/m³ plave na hladině jezera. Jak velká část dřeva se nachází nad hladinou? Kmen zůstane v klidu na hladině, právě když se síla tíhová F_G přesně vyruší se silou vztlakovou F_VZ (tedy když nastane silová rovnováha). Hustotu vody znáte.

Řešení:

Tíhová síla působící na kmen je F_G = mg = 120 kg ⋅ 9,8 N/kg = 1180 N.

Poněvadž kmen setrvává na hladině, nastává silová rovnováha, vztlaková síla je rovna síle tíhové, F_VZ = F_G = 1180 N.

Ze vztahu pro vztlakovou sílu můžeme vypočítat objem ponořené části kmene V₁ = F_VZ/(ϱg)= 1180 N/(1000 kg/m³ ⋅ 9,8 N/kg) = 0,120 m³.

Celkový objem kmene se snadno určí ze vztahu pro hustotu V = m/ϱ = 120 kg/850 kg/m³ = 0,141 m³.

Nad hladinou se tedy nachází objem V₂ = V − V₁ = 0,141 m³ − 0,120 m³ = 0,021 m³, což představuje 15 % celkového objemu.

Kde se setkáme se vztlakovou silou?

Odporová síla

Většina pohybů, které zkoumáme, se děje ve vzduchu. Ať už se jedná o jízdu na kole, pohyb automobilu na dálnici nebo třeba start rakety na vesmírnou misi. Vzduch klade pohybujícímu se tělesu odpor. Působí proti jeho pohybu, brzdí ho stejně jako třecí síla. Pro odpor vzduchu je však typické, že na rozdíl od tření silně závisí na rychlosti pohybujícího se tělesa. Proto se příliš neprojevuje při malých rychlostech a někdy ho můžeme úplně zanedbat. Odporová síla \(\Vec{F}_\mathrm{O}\) působí vždy proti směru rychlosti, jíž se těleso pohybuje vzhledem ke vzduchu (je celkem jedno, jestli se pohybuje těleso nebo vzduch nebo obojí). Tato síla vzniká nárazy proudících molekul na čelní stěnu a současně podtlakem, který se vytváří za obtékaným tělesem.

Vlastnosti odporové síly jsou shrnuty v následující tabulce.

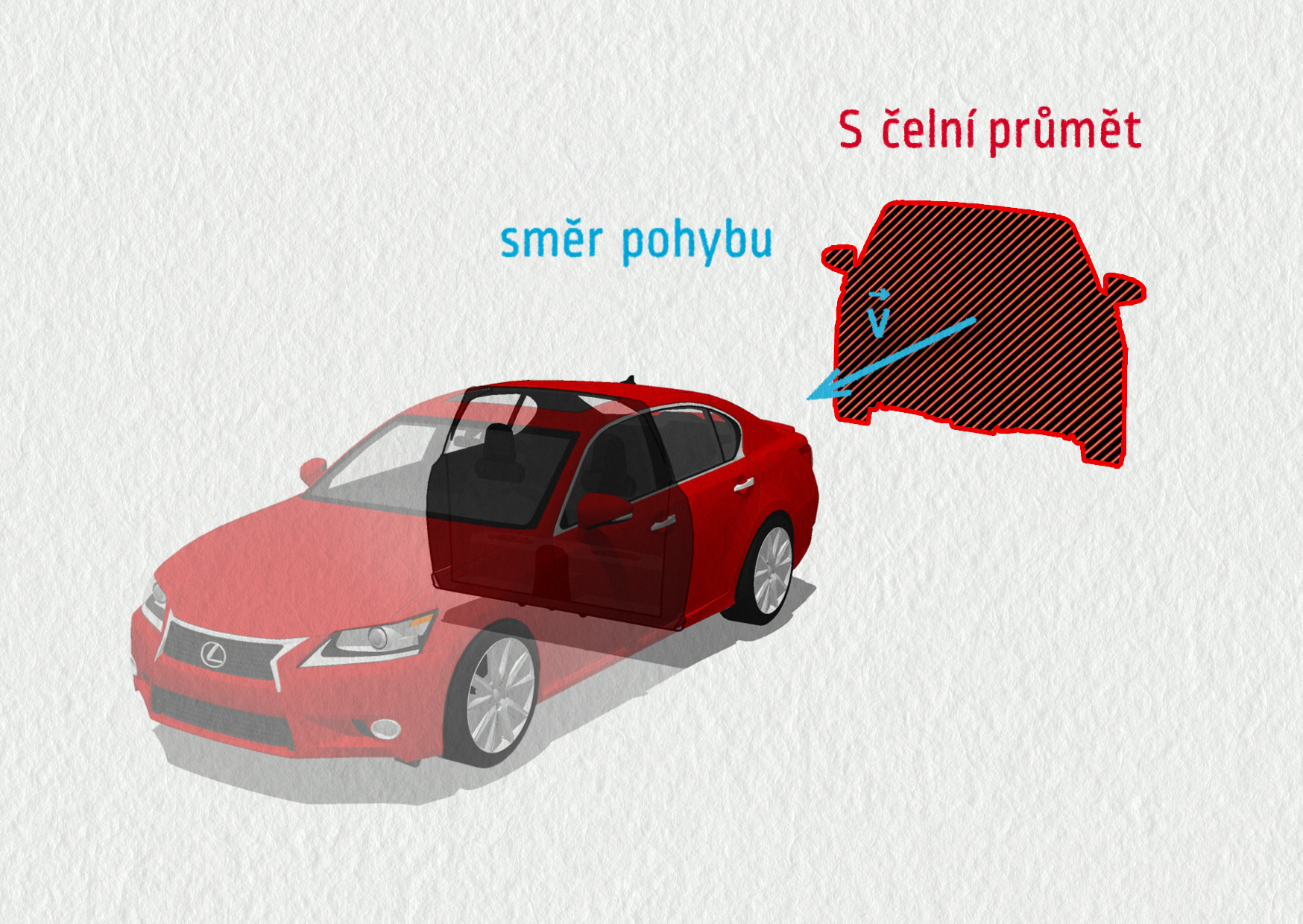
kde ρ je hustota tekutiny (např. vzduchu), S je obsah čelního průmětu tělesa, tj. maximální plocha, která vznikne rozříznutím tělesa kolmo ke směru pohybu. Veličina C se nazývá koeficient odporu a závisí na tvaru tělesa. Jeho hodnota se určuje experimentálně.

Například při navrhování nových automobilů se měří v aerodynamickém tunelu. Konkrétní hodnoty koeficientů odporu najdete v tabulce koeficientů odporu vybraných automobilů a geometrických těles níže. Velmi důležitý je člen v², který ukazuje, že se jedná o kvadratickou závislost síly na rychlosti. Při dvojnásobné rychlosti bude síla čtyřnásobná atd.

Poznámka na okraj: Obtékání těles

S tímto vztahem pro odporovou sílu musíme pracovat vždy, když při obtékání tělesa proudem tekutiny dochází ke vzniku turbulentního proudění za vzniku vírů (například při pohybu automobilů nebo raket, pohybu lodí, pádu dešťových kapek). Při velmi malých rychlostech (kapičky vodní mlhy ve vzduchu, sedimentace drobných částic ve vodě), které zaručí laminární proudění, můžeme použít jednodušší, tzv. Stokesův vzorec, ve kterém velikost odporové síly závisí pouze na první mocnině rychlosti \(F_\mathrm{O}=kv\).

Koeficienty odporu vybraných automobilů a geometrických těles

koeficient odporu C	automobil/těleso	profil
1,4	dutá polokoule proti proudu, padák
1,2	rovinná deska kolmo k proudu
1,1	monopost formule 1
0,54	Mercedes třídy G
0,5	koule
0,41	Volvo 740
0,40	dutá polokoule po proudu
0,38	Citroen ID 19
0,36	Tatra 77
0,26	Jaguar XE
0,22	BMW řady 5
0,19	Volkswagen XL1 (koncept)
0,06	těleso proudnicového tvaru, profil křídla

Činnosti, při kterých je důležité snížit odpor vzduchu

Poznámka na okraj: Přemýšleli jste někdy, proč má golfový míček na povrchu mělké důlky?

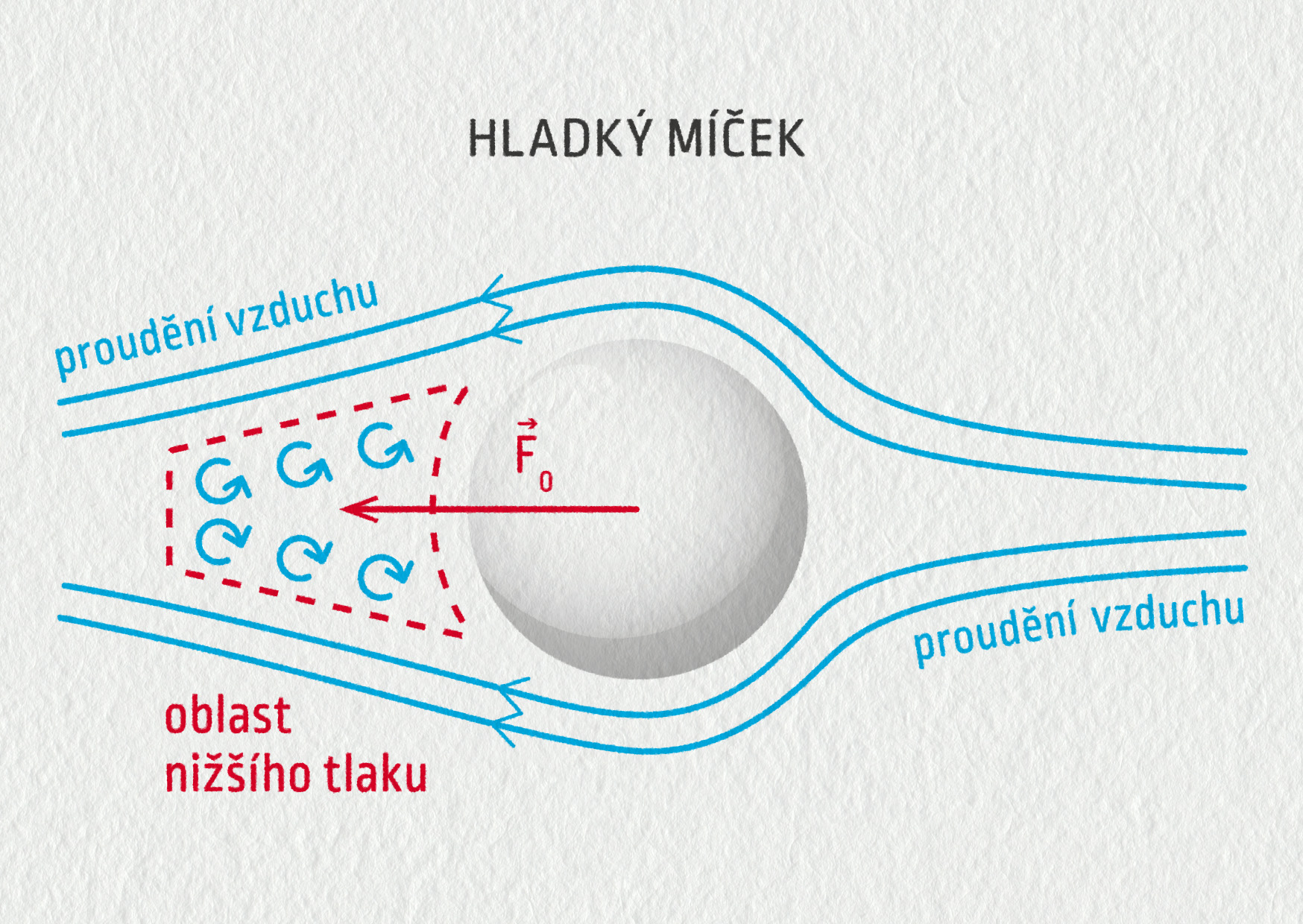
Souvisí to s obtékáním míčku proudem vzduchu. Dobře to můžeme vidět na následujících obrázcích.

V případě hladkého míčku se vzduch, který jej obchází po obou stranách, odtrhne příliš brzy. Za míčkem vznikne poměrně velká oblast nízkého tlaku s množstvím turbulencí, což vede k podstatnému snížení rychlosti míčku.

Jakmile má míček na svém povrchu množství důlků, obtékání vzduchu kolem míčku se zcela změní. Tenká vrstva vzduchu doslova ulpí na jeho povrchu, při obtékání tento nerovný povrch kopíruje a od povrchu míčku se odtrhne později. To vede k tomu, že oblast nízkého tlaku je menší a není takový prostor ke vzniku turbulencí. Odporová síla je znatelně menší a míček doletí mnohem dál.

Více o fyzice v golfu se můžete dozvědět z videí USGA.

Kontrolní otázka

Vyberte všechna správná tvrzení o odporové síle:

Velikost odporové síly nezávisí na tvaru tělesa, ale pouze na jeho velikosti.
Velikost odporové síly je úměrná hmotnosti obtékaného tělesa.
Pohybuje-li se těleso rychleji, je odporová síla větší.
Velikost odporové síly závisí na druhu tekutiny, která těleso obtéká, a na tvaru obtékaného tělesa.

Odeslat  

Příklad 4

Vypočítejte velikost odporové síly pro osobní automobil při rychlostech 90, 120, 150 km/h. Ze zdrojů dostupných na internetu můžeme určit pro automobil Škoda Octavia RS: C = 0,26, S = 2,14 m², hustota vzduchu 1,2 kg/m³.

Řešení:

Pro velikost odporové síly působící na jedoucí automobil platí vztah \(F_\mathrm{O}=\frac{1}{2}C\varrho S v^2\). Číselně vychází pro jednotlivé rychlosti: 206 N, 366 N a 574 N.

Příklad 5

Jedete na kole rychlostí 12 km/h nejdřív proti větru o rychlosti 6 km/h, a poté po větru o rychlosti 6 km/h. Kolikrát větší odporovou sílu budete muset překonávat v prvním případě oproti jízdě po větru?

Řešení:

Budete překonávat 9× větší sílu, protože při jízdě proti větru kolem vás bude proudit vzduch 3× větší rychlostí a odporová síla je úměrná druhé mocnině rychlosti proudění.