Je prakticky nemožné najít těleso, na které by vůbec žádná síla nepůsobila. Muselo by být nekonečně vzdáleno od všech ostatních těles, aby na ně nepůsobila gravitace. Přesto o takto izolovaném tělese hovoříme, pokud je síla zanedbatelně malá, nebo pozorování pohybu trvá tak krátce, že jej síla nestačí ovlivnit (např. vesmírná sonda v meziplanetárním prostoru). Případ, kdy by na těleso působila pouze jediná síla, je u zemského povrchu také poměrně vzácný. Kromě gravitace se totiž často uplatňuje odporová síla vzduchu nebo třecí síla.
Ve většině příkladů na začátku kapitoly jste si mohli všimnout, že na těleso působí několik sil současně. Jaký bude jejich výsledný účinek, když každá působí jiným směrem? Kam se bude těleso pohybovat? Abychom to zjistili, musíme síly složit. To znamená, že je sečteme jako vektory.
Jestliže na těleso působí více sil, můžeme je vektorově sečíst, a určit tak výslednou sílu. Její účinek je stejný, jako by působily všechny jednotlivé síly dohromady, bez ohledu na jejich původ. Tato síla není další novou silou působící na těleso, pouze zjednodušuje studovanou situaci. Místo několika sil a jejich účinků nám stačí studovat jejich výslednici a její účinek.
Pomocí vektorů to můžeme zapsat jednoduše jako \(\Vec{F} = \Vec{F}_1 + \Vec{F}_2 + \Vec{F}_3 + \cdots + \Vec{F}_n\), případně použijeme sumační symbol.
Častokrát tento dlouhý zápis zkracujeme do tvaru \[ \Vec{F} = \sum_{i=1}^{n} \Vec{F}_i = \sum \Vec{F}_i\] (Symbol \(\sum\) je velké řecké písmeno sigma a ve fyzice a matematice znamená sčítání. Čteme „součet“, popřípadě „suma“. Symbol i znamená index dané síly napomáhající k rozlišení jednotlivých sil, n je celkový počet sil.)
Abychom si úlohu zjednodušili, nezajímáme se o rozměry tělesa a o to, v jakém místě na těleso působí. Takové těleso nahradíme hmotným bodem, jak jsme viděli v předchozích kapitole. Někdy to však nejde, a to v situaci, kdy zkoumáme rotační pohyb tělesa. Dohodneme se, že výslednou sílu budeme vždy značit symbolem \(\Vec{F}\), zatímco dílčí síly budeme rozlišovat pomocí indexu (\(\Vec{F}_1\), \(\Vec{F}_\mathrm{t}\), \(\Vec{F}_\mathrm{vz}\), …). Důležité je také odlišovat, zda jde o vektor nebo jeho velikost (uvažte rozdíl mezi zápisy: \(\Vec{F}_1 = \Vec{F}_2\) znamená rovnost dvou sil, zatímco \(F_1 = F_2\) znamená pouze rovnost velikostí dvou sil, o jejichž směrech nevíme nic).
Skládání sil je matematicky vzato sčítání vektorů. Prakticky si ho vysvětlíme na následujících příkladech:
a) síly působící stejným směrem

Zdroj


Zdroj
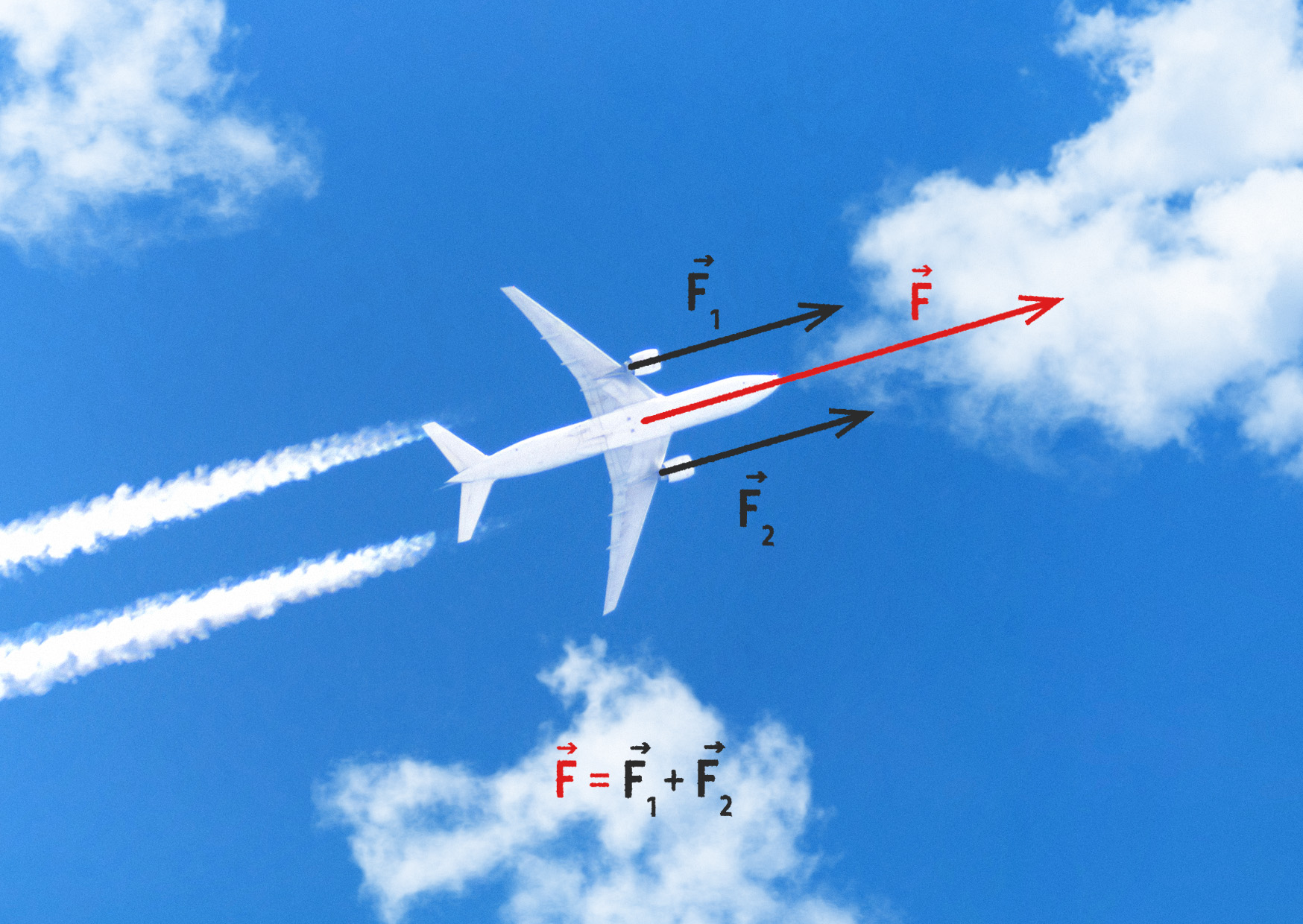
S takovou situací se setkáváme zcela běžně. Dva motory dopravního letadla, každý působí na letadlo tahovou silou o velikosti 120 kN. Protože působí stejným směrem, je celková síla rovna jejich součtu F = F1 + F2 = 120 kN + 120 kN = 240 kN.
Na druhém obrázku každý ze psů táhne silou o velikosti F1 = 50 N a dohromady jsou saně taženy silou o velikosti F = 2 ⋅ 50 N = 100 N. Závěr? Působí-li síly stejným směrem, sčítáme velikosti sil. F = F1 + F2.
4.12 – Skládání dvou sil stejného směru. Silové působení na těleso zakreslujeme do tzv. silového diagramu. V něm je těleso nahrazeno hmotným bodem a všechny síly působí v tomto bodě, abychom je mohli snadno skládat.
Zdroj
b) síly působící opačnými směry
Každý z nás se již někdy přetahoval lanem. Když jsou oba týmy stejně silné, tahají za konce lana opačnými a stejně velkými silami. V takovém případě se působící síly zcela vyruší. Výsledná síla je nulová.


Zdroj
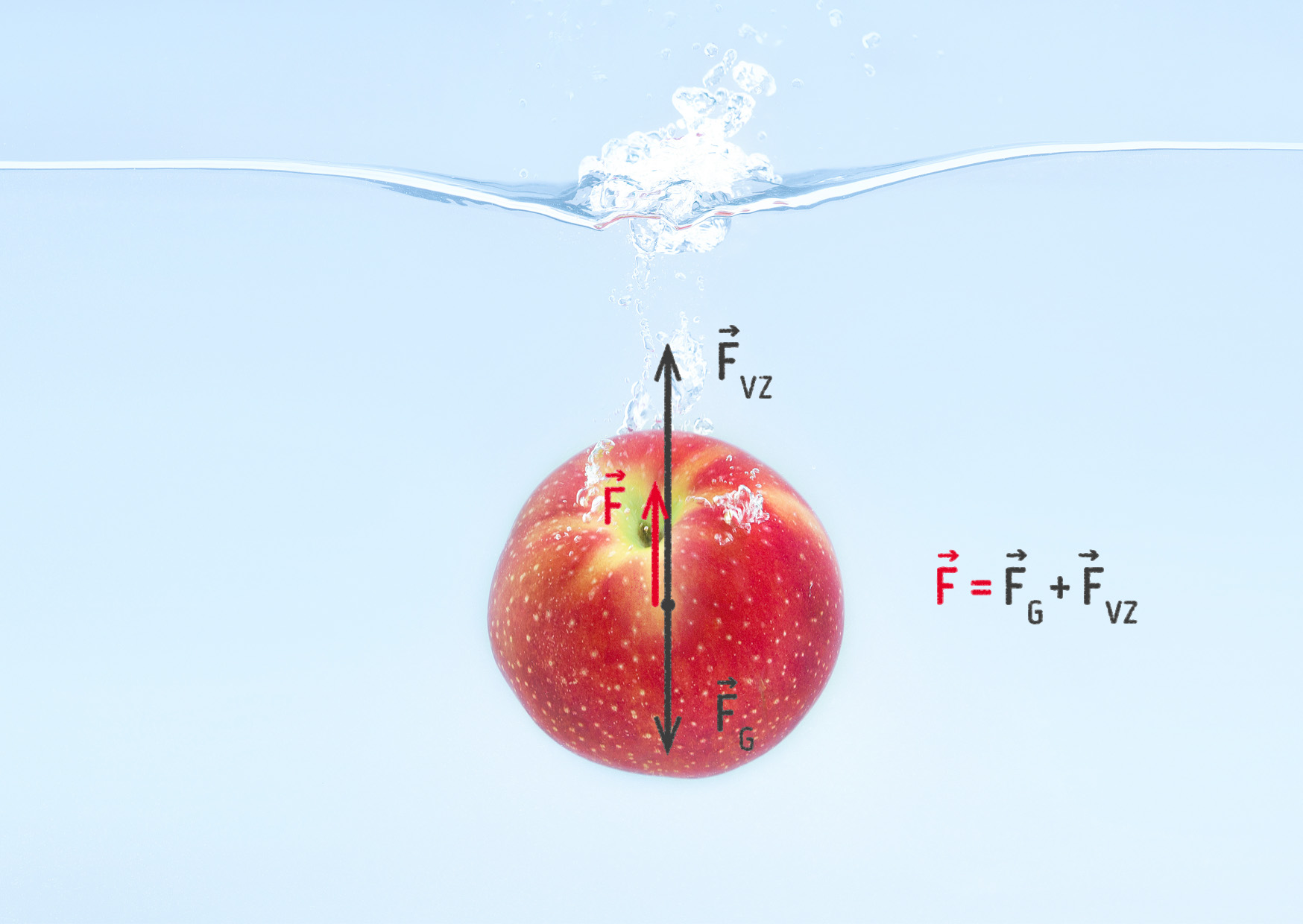
Co když ale síly nejsou stejně velké? V tom případě jejich složením vznikne síla, která směřuje ve směru větší z nich a její velikost je rovna rozdílu velikostí působících sil. Vše si můžete prohlédnout na následujícím obrázku 4.14. Tíhová síla táhne jablko svisle dolů, vztlaková síla svisle vzhůru, odporovou sílu zanedbáváme. Protože je velikost vztlakové síly o něco větší než tíhové, výslednice bude směřovat vzhůru. Důsledkem čehož pak je, že jablko vhozené do vody vyplave na její povrch.
Závěr? Mají-li síly opačný směr, odečítáme jejich velikosti. Výsledná síla směřuje ve směru větší z nich.

Zdroj
c) navzájem kolmé síly
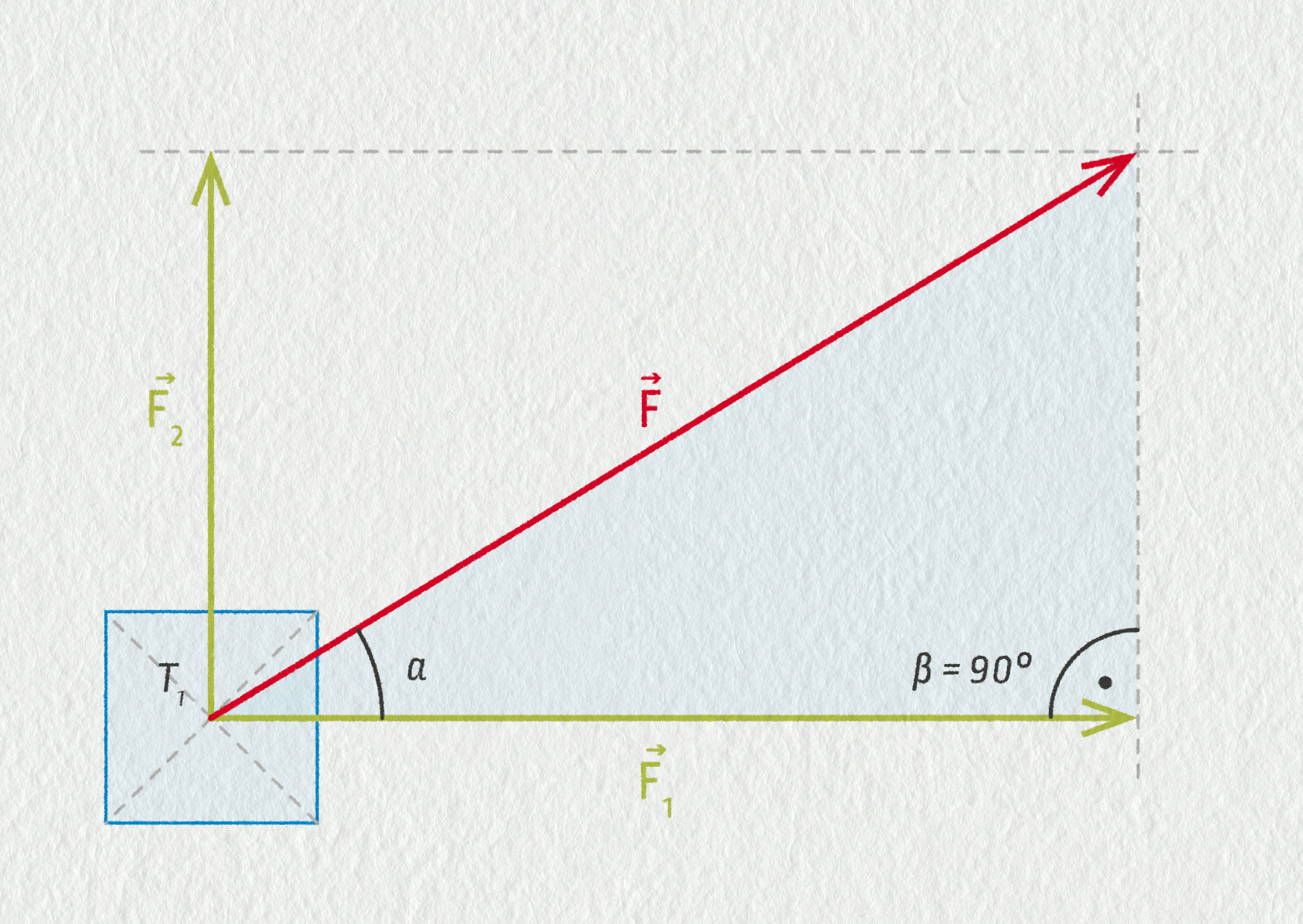
Jiná situace nastává, jestliže jsou dvě působící síly na sebe kolmé. V tomto případě si pomůžeme geometrickou konstrukcí – sestrojíme silový rovnoběžník: působiště sil umístíme do stejného bodu, doplníme na rovnoběžník a výslednice sil je úhlopříčkou rovnoběžníku. Určili jsme její směr i velikost.
4.15 – Skládání dvou sil
Zdroj
Velikost výsledné síly můžeme také spočítat. Působící síly \(\Vec{F}_1\) a \(\Vec{F}_2\) tvoří pravoúhlý trojúhelník, výslednice \(\Vec{F}\) je přeponou tohoto trojúhelníka. Lze tedy použít Pythagorovu větu a pro velikost výsledné síly platí: \( F=\sqrt{F_1^2+F_2^2}\). Můžeme vypočítat i velikost úhlu, který svírá výslednice se směrem jedné nebo druhé síly.
Zdroj
Vyzkoušejte si to na následující situaci.
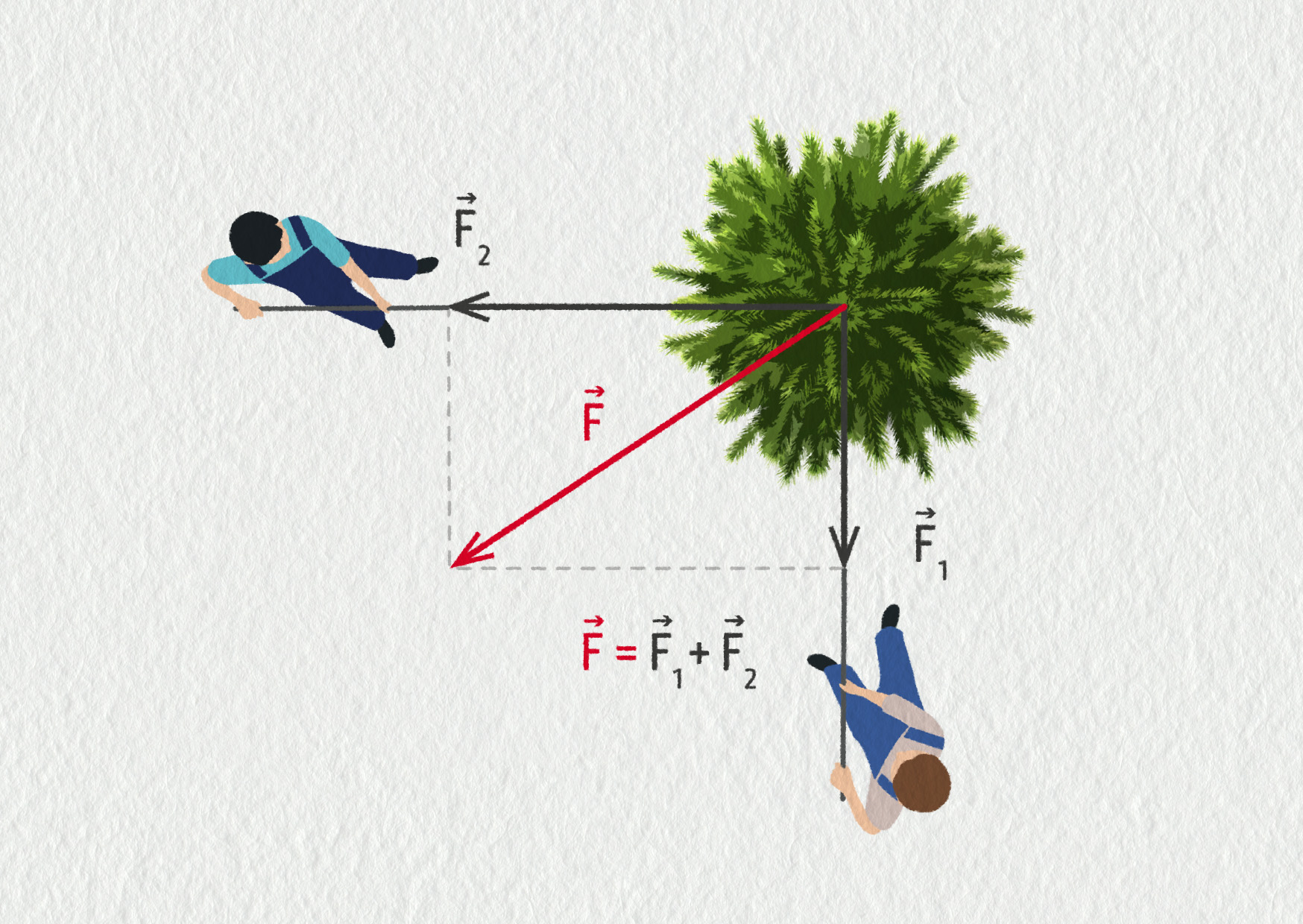
Příklad: Při kácení stromů je vždy nutné zajistit, aby kácený strom padal správným směrem. Požadovanému směru můžeme pomoci tak, že na strom přivážeme dvě lana a táhneme ve směrech na sebe kolmých. Jestliže na jedno z lan budeme působit silou F1 = 150 N a na druhé (kolmé k prvnímu) silou F2 = 200 N, jak bude velká jejich výslednice?
Zdroj
Velikost výsledné síly určíme pomocí Pythagorovy věty:
\[ F=\sqrt{F_1^2+F_2^2} = \sqrt{150^2+200^2}\ \mathrm{N} = 250\ \mathrm{N} \]d) obecný úhel
Často však působící síly nejsou ani rovnoběžné, ani kolmé. Jak tedy postupovat, abychom vyřešili tuto situaci? Použijme opět geometrickou konstrukci jako v předchozí situaci kolmých sil. Síly vycházející ze stejného bodu doplníme na rovnoběžník a výsledná síla je jeho úhlopříčkou. Chceme-li znát její velikost, musíme změřit její délku a podle měřítka (např. \(1\ \mathrm{cm}\mathrel{\widehat{=}}15\ \mathrm{N}\)) přepočítat výslednou velikost. Například změříme délku výslednice 8,4 cm a pro velikost výslednice dostáváme F = 8,4 ⋅ 15 N = 126 N.
4.18 – Skládání vektorů
Zdroj
Takovéto grafické skládání sil není jedinou možností. Velikost výsledné síly je možné určit také početně. V tomto případě použijeme věty o obecném trojúhelníku a použijeme sinovou nebo kosinovou větu. Více najdete v rozšiřujícím článku.
Příklad: Máte na vodítku dva psy, Alík táhne silou \(\Vec{F}_\mathrm{A}\) o velikost 20 N, Bobík silou \(\Vec{F}_\mathrm{B}\) o velikosti 30 N. Zakreslete výslednou sílu a napište, co platí pro její velikost v těchto případech:
Psi táhnou
- stejným směrem,
- opačným směrem,
- kolmo,
- tak, že vodítka svírají úhel 60°.

Zdroj
Ad a) Jestliže psi táhnou stejným směrem, stačí sečíst velikosti obou působících sil. Dostaneme tedy F = FA + FB = 20 N + 30 N = 50 N.
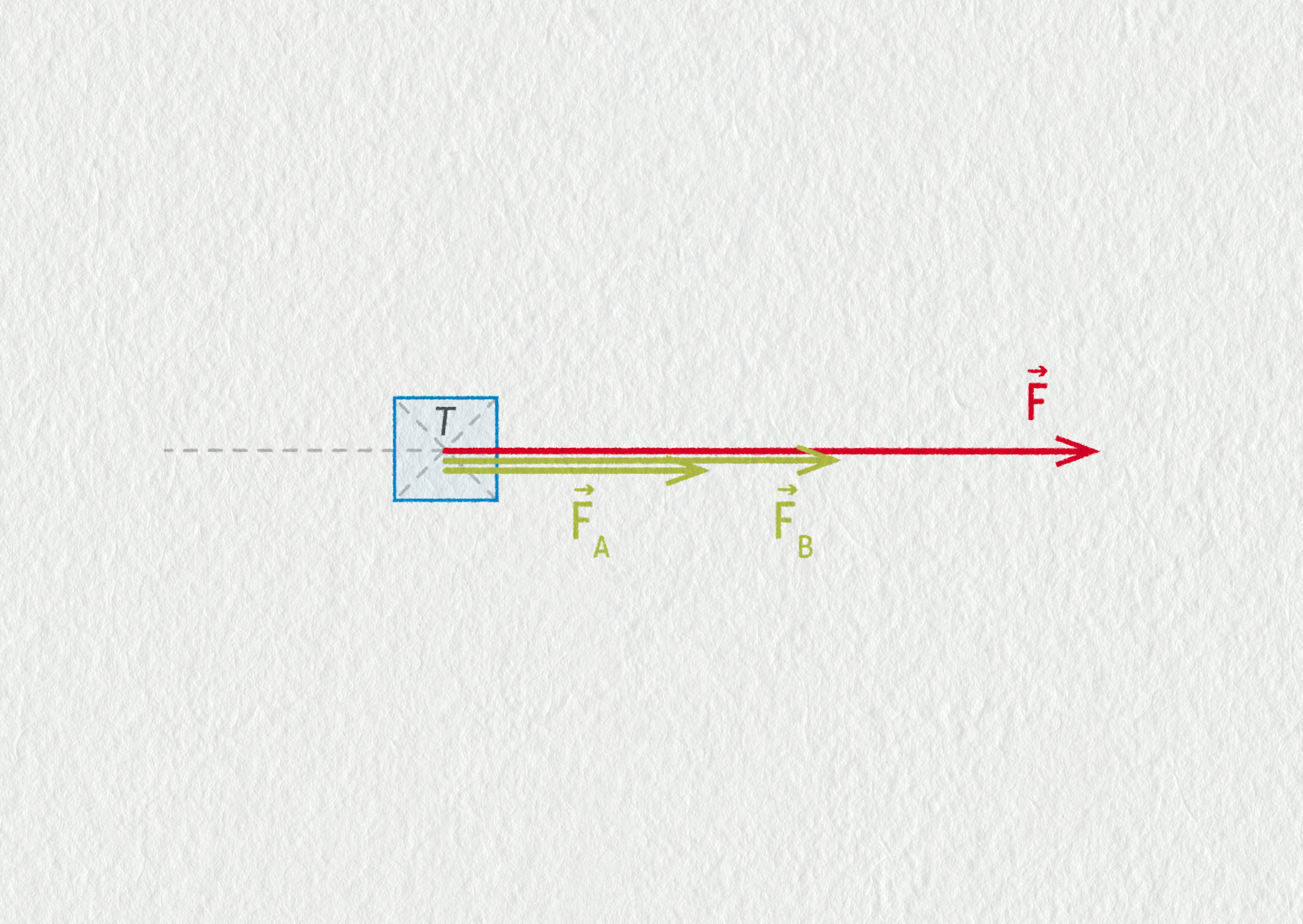
Zdroj
Ad b) Jestliže psi táhnou opačným směrem, od větší síly odečteme menší. Výsledná síla pak směřuje ve směru větší síly. Číselně tedy dostáváme: F = FB - FA = 30 N − 20 N = 10 N.

Zdroj
Ad c) Táhnou-li oba psi ve směrech navzájem kolmých, velikost výsledné síly získáme použitím Pythagorovy věty: \[ F=\sqrt{F_\mathrm{A}^2+F_\mathrm{B}^2} = \sqrt{20^2+30^2}\ \mathrm{N} \approx 36\ \mathrm{N} \]

Zdroj
Ad d) V obecném případě, kdy je mezi vodítky táhnoucích psů úhel 60°, si pomůžeme grafickou konstrukcí, jak je znázorněno na následujícím obrázku. Hodnota výsledné síly je 44 N a svírá se směrem síly \(\Vec{F}_\mathrm{A}\) úhel o velikosti 36,6°.
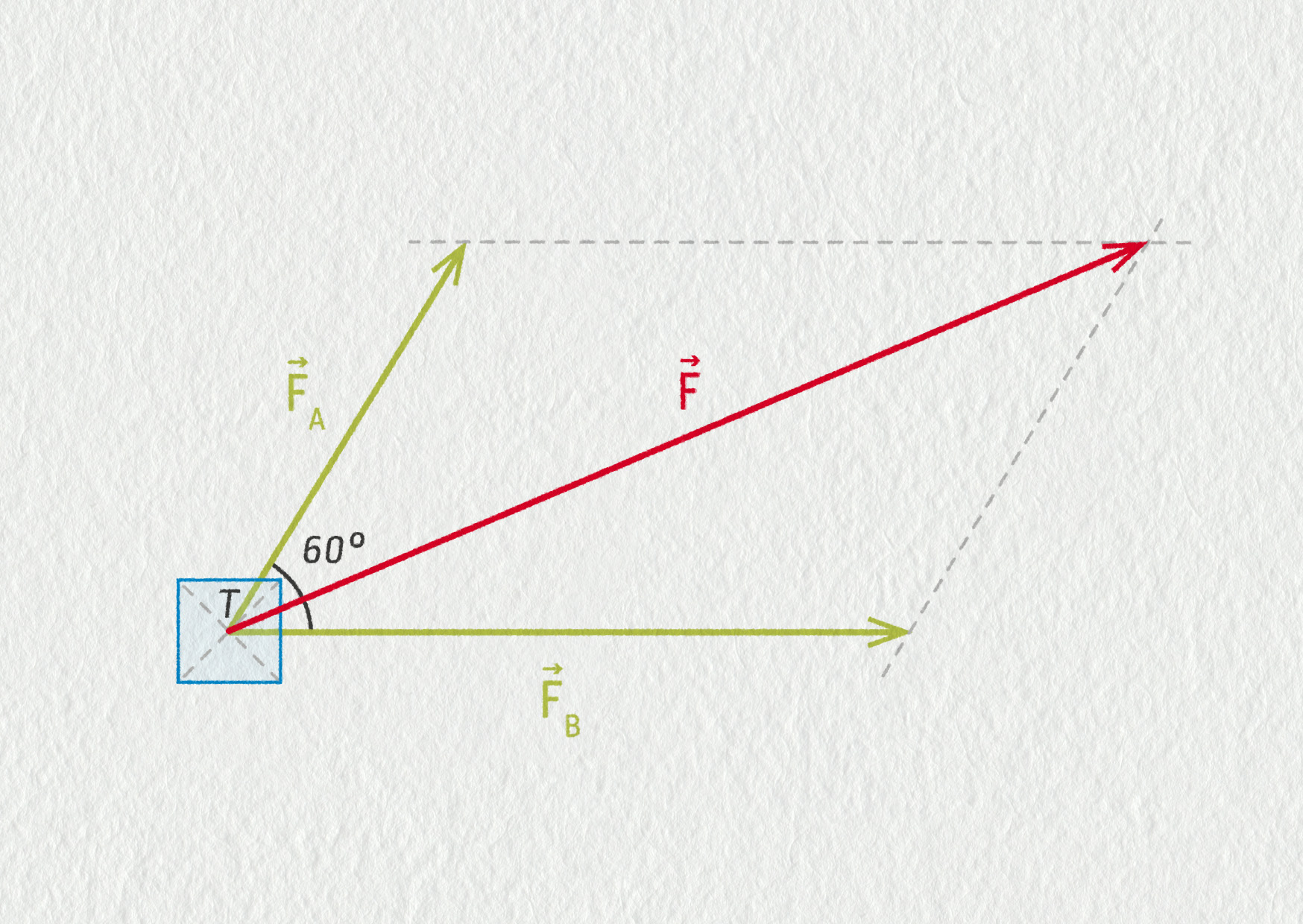
Zdroj

