Ve třetí kapitole jsme se zabývali pouze pohyby po přímce. Nyní budeme chtít popsat pohyby v rovině nebo v prostoru, a proto musíme použít vektorové veličiny: polohový vektor \(\Vec{r}\), vektor rychlosti \(\Vec{v}\) a vektor zrychlení \(\Vec{a}\). Těleso jsme nahradili hmotným bodem, stejně tak tomu bude i v této kapitole.
Při popisu pohybu se snažíme nejprve určit, kde se těleso nachází. K určení polohy nám dobře slouží soustava kartézských souřadnic. Tato soustava se skládá z počátku O a několika os, které jsou na sebe navzájem kolmé a na nichž jsme určili jednotkovou vzdálenost.
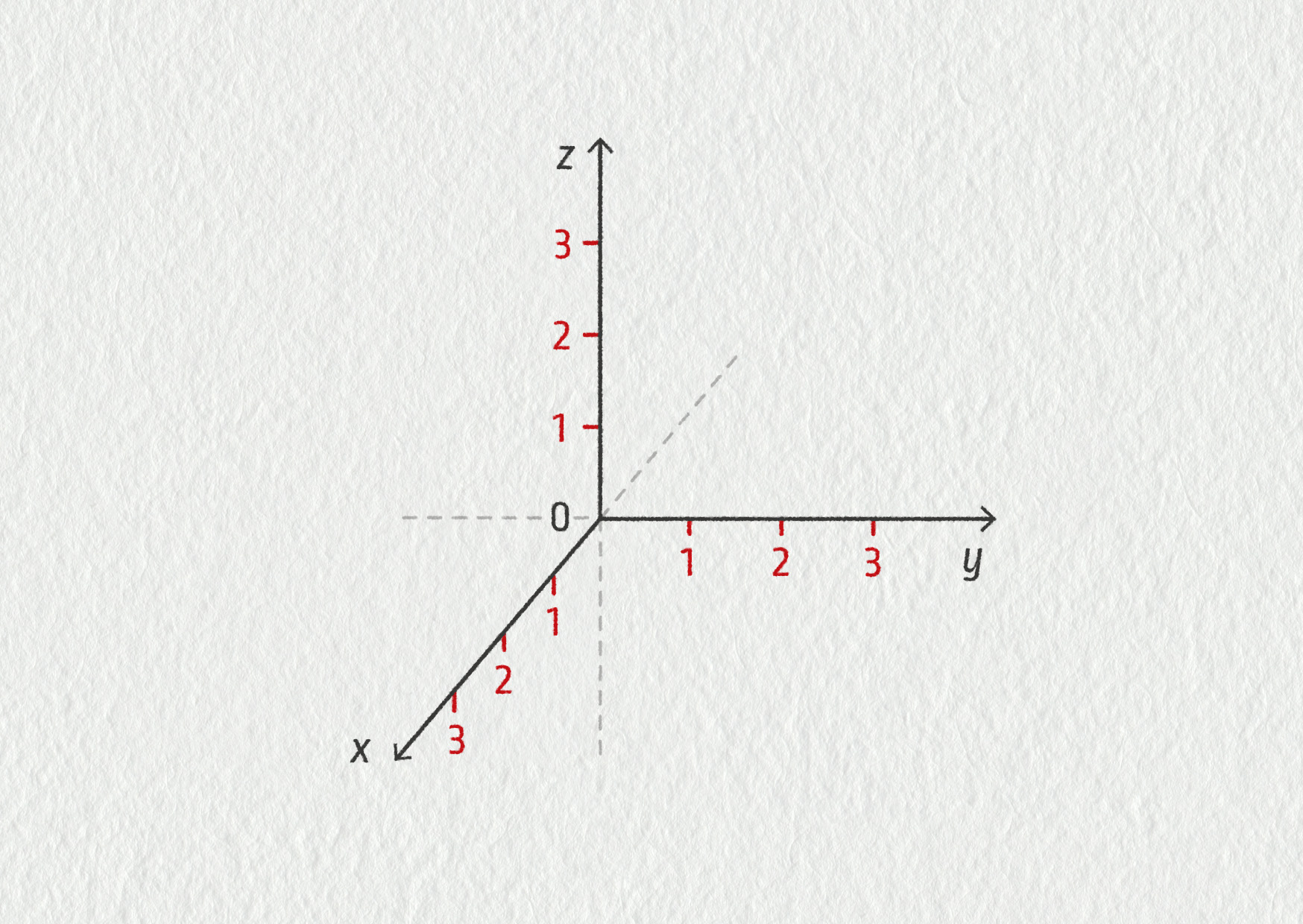
Zdroj
Polohový vektor \(\Vec{r}=\overrightarrow{OM}=(x_M,y_M,z_M)\).
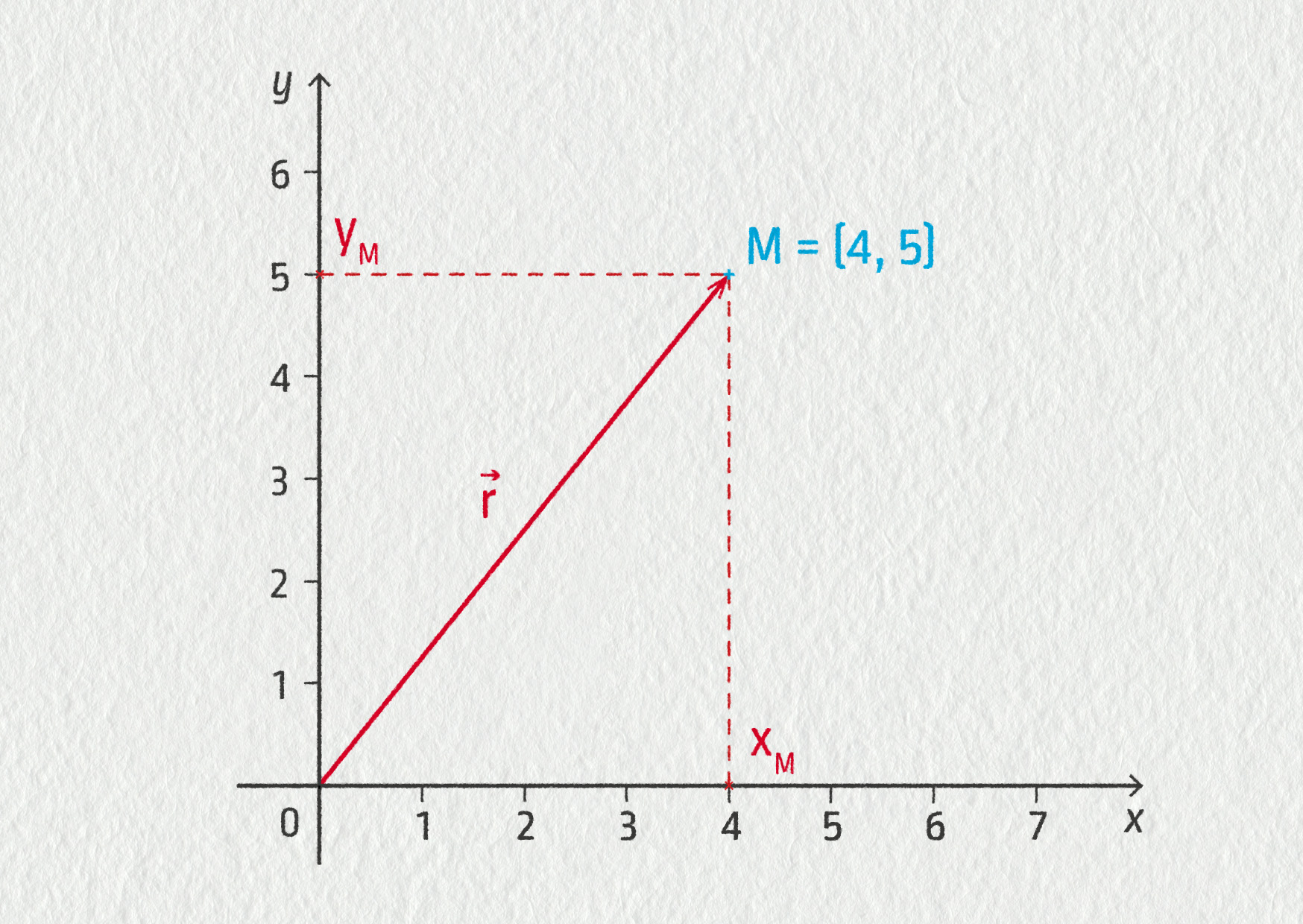
Polohový vektor je definován jako vektor, který začíná v počátku soustavy souřadnic a končí v bodě M, jehož polohu určujeme. Podívejme se, jak můžeme určit polohu bodu M v rovině (2D) nebo v prostoru (3D).
Zdroj

Zdroj
Odkaz na soubor v Geogebře: https://www.geogebra.org/3d/egbuvvcy
Pomocí kartézské soustavy souřadné vyjádříme polohový vektor následující způsobem: \(\Vec{r}=\overrightarrow{OM}=(x_M,y_M,z_M)\). Vidíme, že složky polohového vektoru odpovídají souřadnicím bodu M. To je možné právě proto, že polohový vektor začíná v počátku soustavy souřadnic \(O=(0,0,0)\). V následujícím textu budeme právě tímto způsobem zapisovat složky vektorů: \(\Vec{r}=\overrightarrow{OM}=(2\ \mathrm{m};4\ \mathrm{m};5\ \mathrm{m})\). Nesmíme zapomínat, že složky polohového vektoru představují vzdálenosti ve směru dané osy, a proto jde o čísla s odpovídající jednotkou, například cm nebo m.
Délka polohového vektoru představuje vzdálenost bodu M od počátku souřadnic. Vypočítat ji můžeme pomocí Pythagorovy věty zobecněné do 3D:
\[ r = |OM| = \sqrt{x_M^2+y_M^2+z_M^2} \]Na obrázku vidíte záznam polohy v rovině tří dopravních letadel na letišti Václava Havla v Praze-Ruzyni. (K tomuto obrázku se vztahují všechny tři kontrolní otázky níže.)
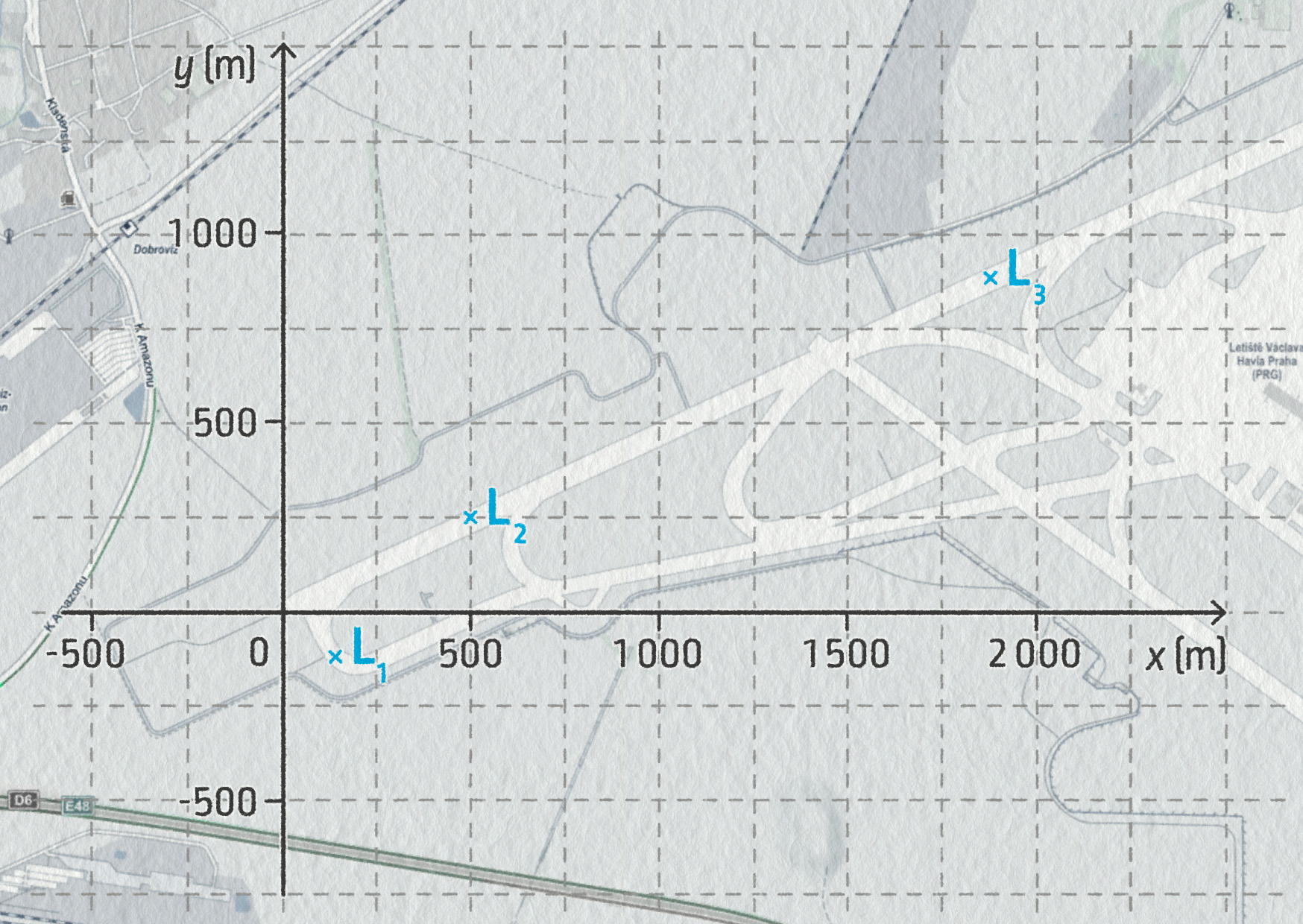
Zdroj
Pokud pohyb probíhá v rovině, pak si při správné volbě vztažné soustavy vystačíme pouze se souřadnicemi \((x,y)\). Poslední souřadnice \(z=0\), proto ji dále nemusíme zapisovat. Právě takové pohyby budeme studovat v této kapitole.
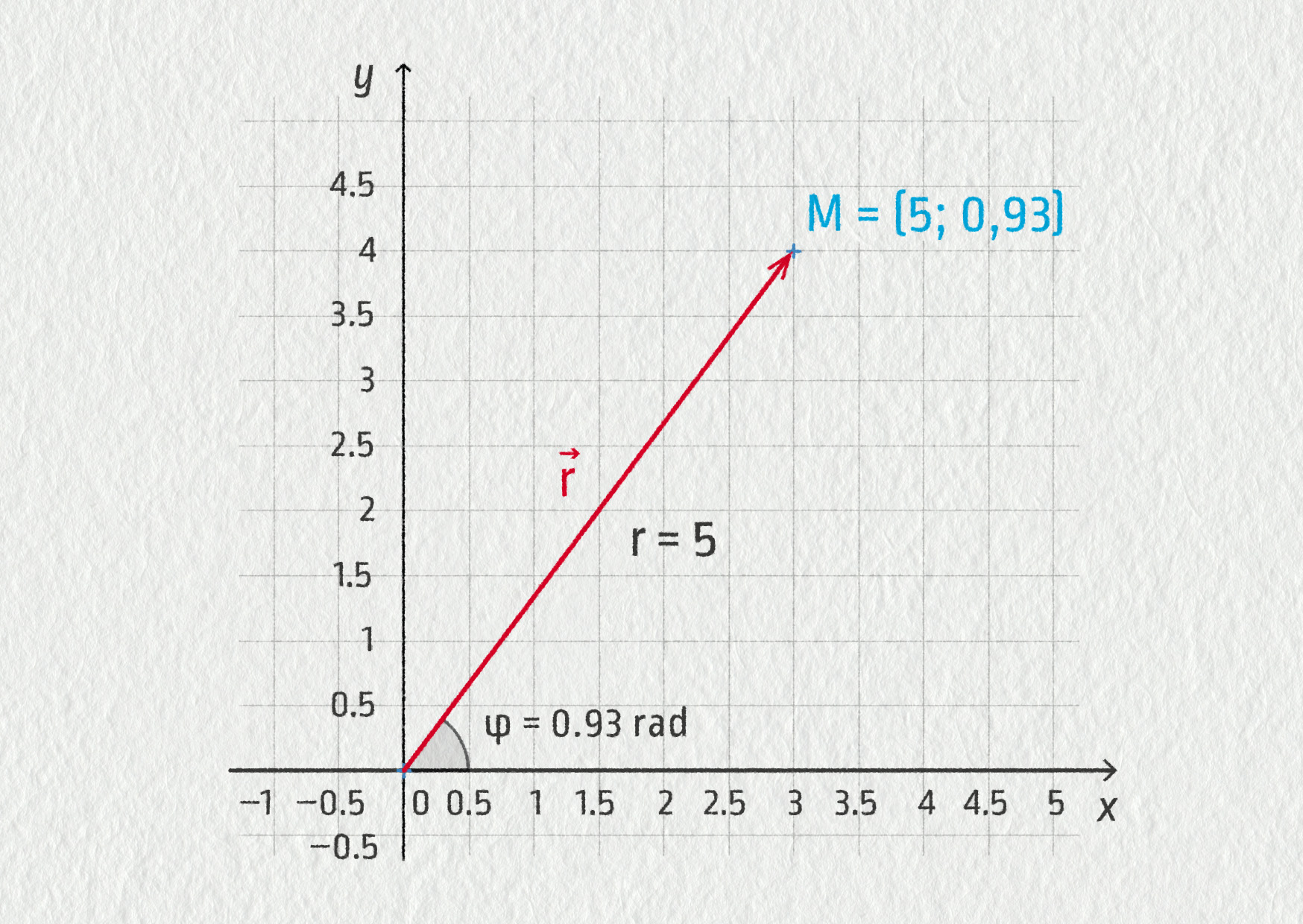
Kartézská soustava je pravoúhlá. Pokud chceme popsat pohyb, který probíhá po kružnici, je lepší použít polární souřadnice \((r,\varphi)\), kde souřadnice \(r\) určuje vzdálenost tělesa od počátku a úhel \(\varphi\) je úhel, který svírá polohový vektor \(\Vec{r}\) se zvolenou osou, nejčastěji osou \(x\) v kartézské soustavě. V tomto případě je velikost první souřadnice \(r\) stále stejná (poloměr kružnice = \(r\)) a k popisu pohybu po kružnici nám postačuje sledovat změny souřadnice \(\varphi\).

Zdroj
Zdroj
Pro přechod od kartézských souřadnic k polárním souřadnicím využíváme následující vztahy, které vyplývají z obrázku:
\[ r_M = \sqrt{x_M^2+y_M^2}\;,\qquad \tan\varphi_M=\frac{y_M}{x_M}\;. \]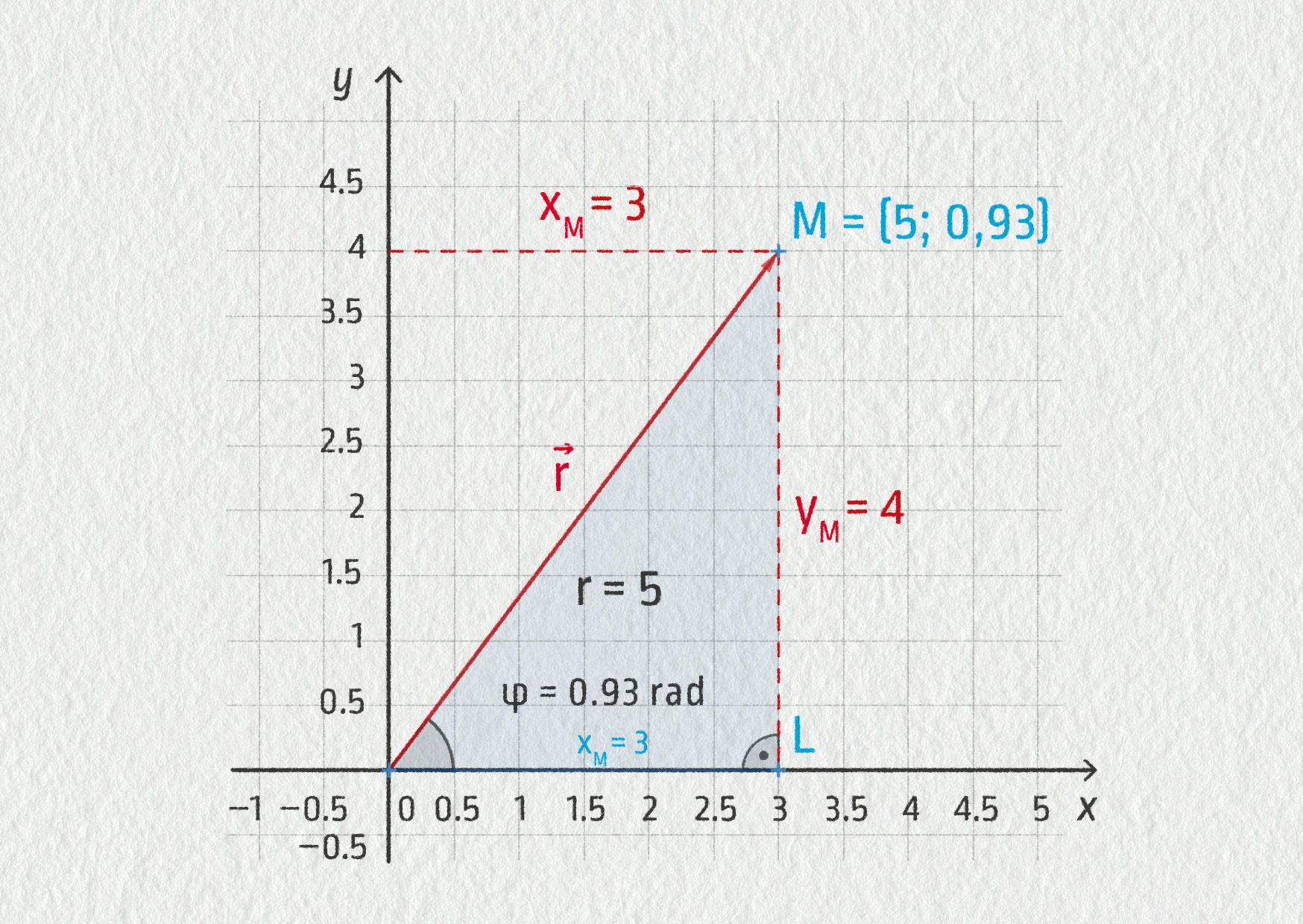
Zdroj
Souřadnice \(r_M\) odpovídá velikosti přepony v pravoúhlém trojúhelníku OLM, kde odvěsny jsou rovny souřadnicím bodu M. Podíl protilehlé \(y_M\) a přilehlé odvěsny \(x_M\) tohoto trojúhelníka odpovídá funkci \(\tan\varphi\).
Pro přepočet polárních souřadnic na kartézské pak můžeme využít funkcí sinus a kosinus ve stejném pravoúhlém trojúhelníku OLM:
\[ x_M = r_M\cos\varphi_M \quad\hbox{a}\quad y_M = r_M\sin\varphi_M\;. \]Máme-li popsat polohu tělesa v prostoru, můžeme využít válcové souřadnice \((r,\varphi,z)\) nebo sférické souřadnice \((r,\vartheta,\varphi)\).
Převod z kartézských do polárních souřadnic a zpět si můžete vyzkoušet zde:
-
Převod z kartézských souřadnic bodu M \((-2\ \mathrm{cm};4\ \mathrm{cm})\) do polárních:
\[ \begin{aligned} r_M &= \sqrt{x_M^2+y_M^2} = \sqrt{(-2)^2+4^2}\ \mathrm{cm} = \sqrt{20}\ \mathrm{cm}=2\sqrt{5}\ \mathrm{cm}\;, \\ \tan\varphi_M &= \frac{y_M}{x_M} = \frac{4}{-2} = -2\;, \\ \end{aligned} \]odtud pak vyjádříme \(\varphi=-1{,}1\ \mathrm{rad}\).
Polární souřadnice bodu M jsou \((2\sqrt{5}\ \mathrm{cm};-1{,}1\ \mathrm{rad})\).
-
Převod polárních N \((3{,}1\ \mathrm{cm};1{,}2\ \mathrm{rad})\) do kartézských:
První polární souřadnice bodu N je jeho vzdálenost od počátku \(r_N=3{,}1\ \mathrm{m}\) a druhá je velikost úhlu v radiánech \(\varphi_N=1{,}2\ \mathrm{rad}\). Pro výpočet kartézských souřadnic použijeme vztahy
\[ \begin{aligned} x_N &= r_N\cos\varphi_N = 3{,}1\ \mathrm{cm}\cdot\cos(1{,}2) = 1{,}1\ \mathrm{cm} \\ y_N &= r_N\sin\varphi_N = 3{,}1\ \mathrm{cm}\cdot\sin(1{,}2) = 2{,}9\ \mathrm{cm} \\ \end{aligned} \]Kartézské souřadnice bodu N tedy jsou \((1{,}1\ \mathrm{cm}; 2{,}9\ \mathrm{cm})\).
Podívejme se, co se děje s polohovým vektorem, když se těleso pohybuje. Názornou představu si můžete udělat v následující animaci: https://www.geogebra.org/calculator/vpht6skg. Polohový vektor \(\Vec{r}\) mění svůj směr i velikost.
Zdroj
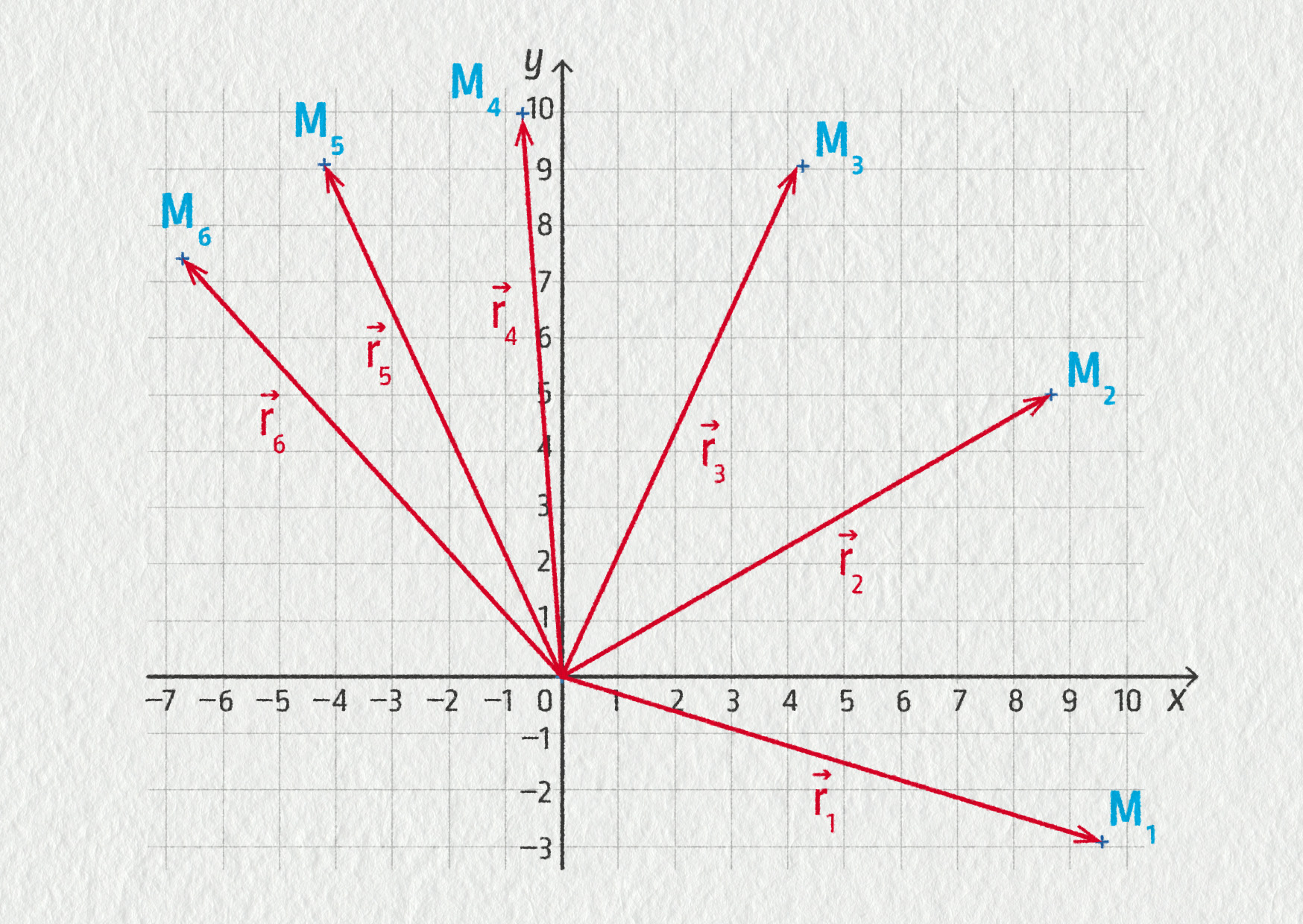
V následující tabulce jsou zapsány souřadnice \(x\) a \(y\) hmotného bodu. Mezi záznamem jednotlivých bodů uplynul čas 0,20 s.
- Narýsujte polohový vektor v jednotlivých pozicích hmotného bodu.
- Určete, zda se hmotný bod pohybuje. Jestliže ano, po jaké křivce?
| x (cm) | y (cm) | |
|---|---|---|
| r1 | 9,6 | −2,9 |
| r2 | 8,7 | 5,0 |
| r3 | 4,3 | 9,0 |
| r4 | −0,7 | 10 |
| r5 | −4,2 | 9,1 |
| r6 | −6,7 | 7,4 |
a) Polohový vektor je na následujícím obrázku:
Zdroj
b) Hmotný bod se pohybuje, vidíme, že polohový vektor se otáčí. Křivka, po níž se hmotný bod pohybuje, je část kružnice se středem v bodě O. Výpočtem lze ověřit, že délka polohového vektoru čili vzdálenost od počátku je stále stejná:
\[ r_1 = \sqrt{9{,}6^2+(-2{,}9)^2}\ \mathrm{cm} = 10\ \mathrm{cm}\;, \]stejně tak i pro ostatní polohové vektory.
Vezmeme-li v uvahu množinu všech bodů, kde se hmotný bod v průběhu svého pohybu (v různých časech) nacházel, získáme spojitou křivku, která se nazývá trajektorie. V naší první ukázce, kdy je trajektorií část přímky, jde o přímočarý pohyb. V řešeném příkladu jsme studovali pohyb po kružnici se středem v bodě O. Jak najít střed kruhové trajektorie, to si můžete vyzkoušet v laboratorní práci.
Několik příkladů trajektorie hmotného bodu

Zdroj

Zdroj

Zdroj

Zdroj
Zdroj
Důležitou veličinou popisující pohyb je vektor posunutí \(\Delta\Vec{r}\).
Vyjadřuje změnu polohy tělesa, jak vidíme na následujícím obrázku záznamu pohybu v rovině.
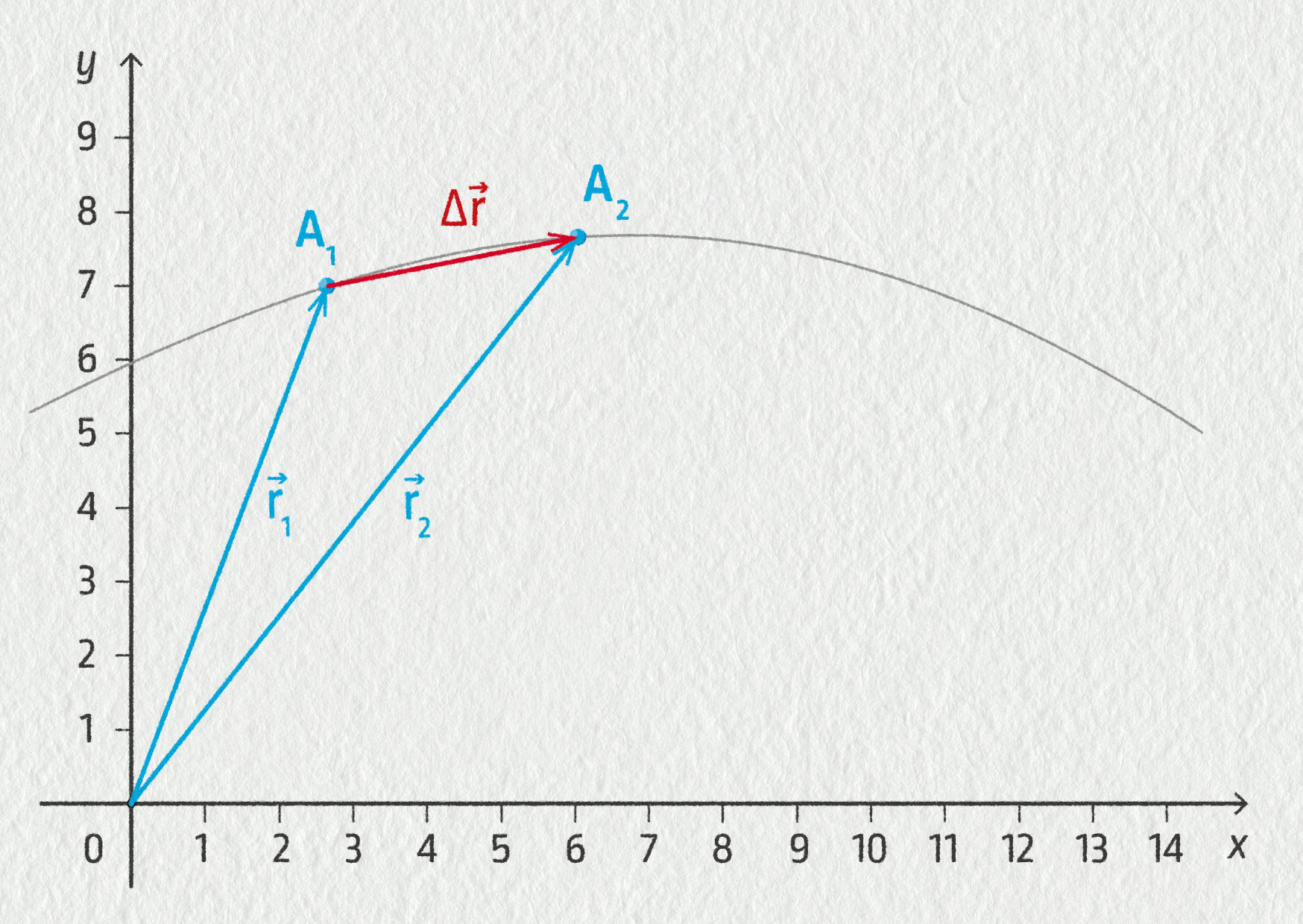
Zdroj
Vektor posunutí \(\Delta\Vec{r}=\Vec{r}_2-\Vec{r}_1\)
Vektor posunutí je definován jako rozdíl dvou vektorů, proto i jeho složky získáme odečtením složek polohových vektorů \(\Vec{r}_1\) a \(\Vec{r}_2\):
\[ \Delta\Vec{r} = (\Delta x,\Delta y) = (x_2-x_1,y_2-y_1)\;. \]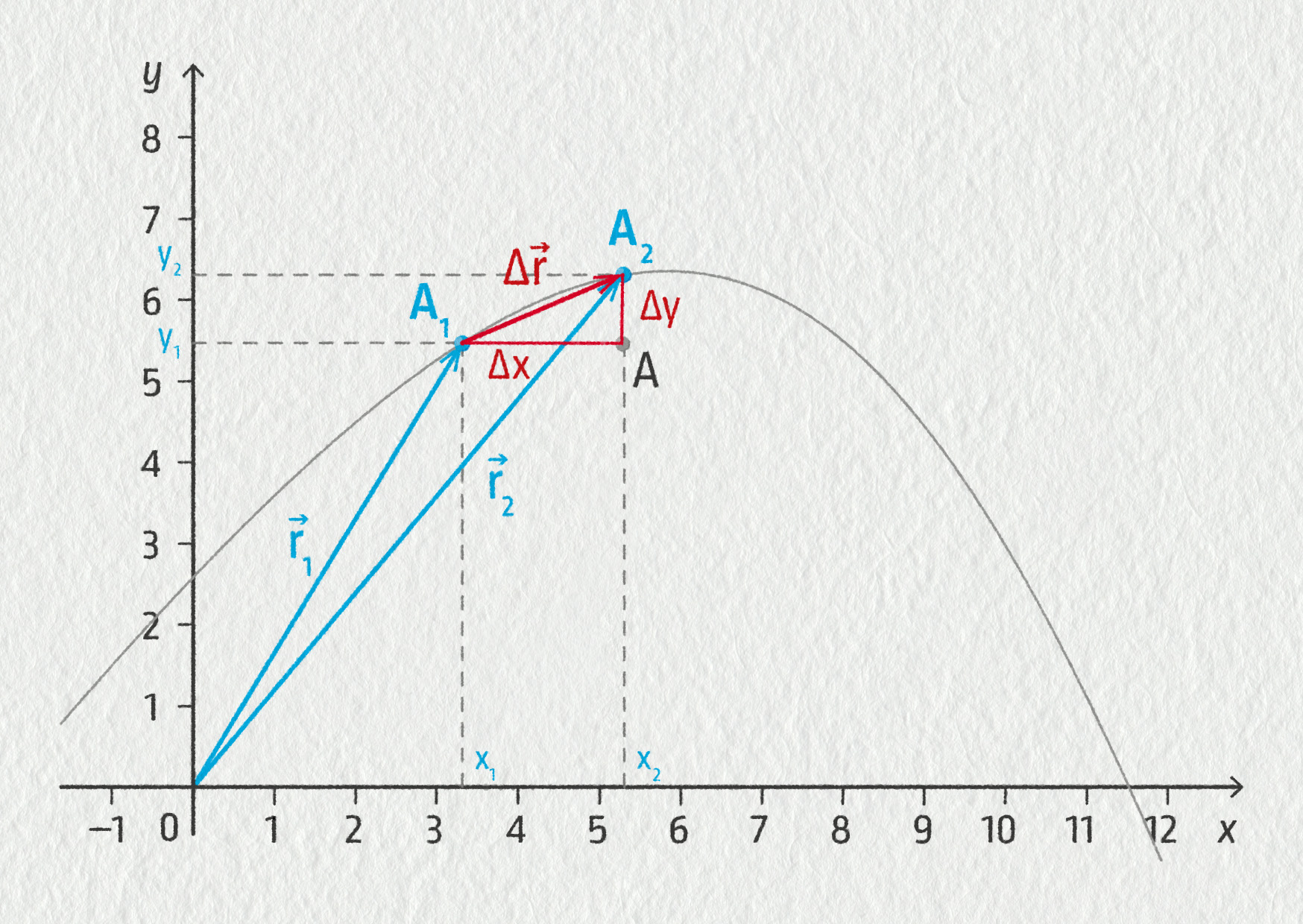
Zdroj
Na následujícím obrázku vidíme rovný úsek železniční trati mezi Velimí a Pečkami. Vlak vyjíždí z Velimi v 10:08 a zastavuje v Pečkách v 10:24. Jeden čtvereček na mapě znázorňuje plochu 1000x1000 m.
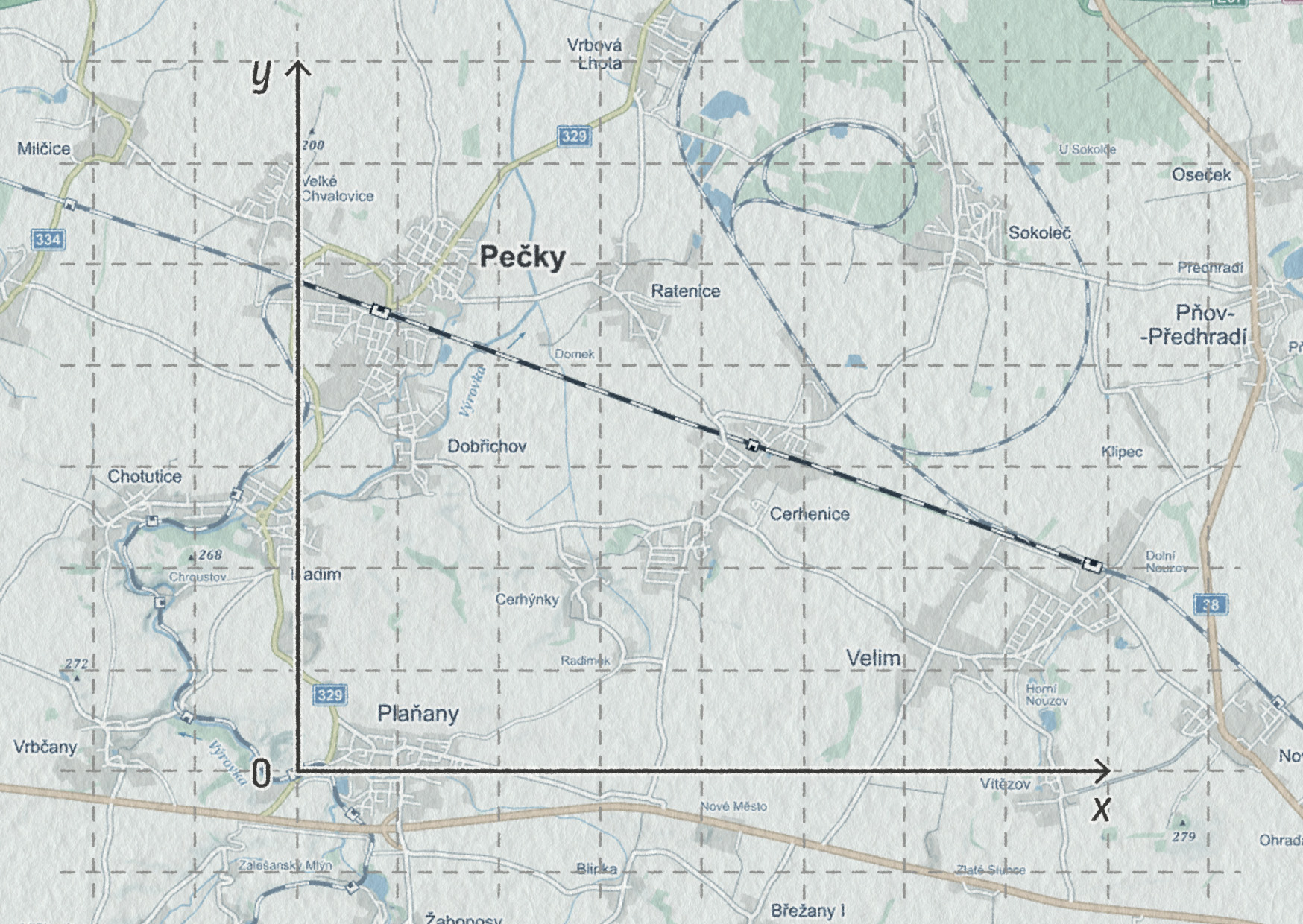
Zdroj
- Určete polohový vektoru vlaku ve stanici Velim a poté ve stanici Pečky.
- Vypočítejte složky vektoru posunutí \(\Delta\Vec{r}\).
- Zakreslete počáteční a koncovou polohu a vektor posunutí do obrázku.
a) Poloha stanice Velim: \(\Vec{r}_1=(7800\ \mathrm{m};2000\ \mathrm{m})\), poloha stanice Pečky: \(\Vec{r}_2=(800\ \mathrm{m};4500\ \mathrm{m})\).
b) Vektor posunutí má složky:
\[ \Delta\Vec{r} = \Vec{r}_2-\Vec{r}_1 = (800\ \mathrm{m}-7800\ \mathrm{m};4500\ \mathrm{m}-2000\ \mathrm{m})=(-7000\ \mathrm{m};2500\ \mathrm{m}) \]c) Zákres vektorů do obrázku:

Zdroj
I kdyby trať nebyla přímočará, vektor posunutí se nezmění, neboť závisí jen na počáteční a koncové poloze vlaku.
Vektor posunutí \(\Delta\Vec{r}\) narýsujeme tak, že spojíme šipkou počáteční a koncový bod. V této poznámce dokážeme, že toto pravidlo odpovídá jeho definici \(\Delta\Vec{r}=\Vec{r}_2-\Vec{r}_1\).
Tento vektor získáme tak, že odečteme polohové vektory ve dvou uvažovaných bodech:
\[ \Delta\Vec{r} = \Vec{r}_2 - \Vec{r}_1 = \Vec{r}_2 + (-\Vec{r}_1)\;. \]Sečíst dva vektory již umíme, stačí je doplnit na rovnoběžník. Výsledný vektor pak bude odpovídat vektoru, který začíná v prvním studovaném bodě a končí v druhém z nich. V našem případě \(\Delta\Vec{r}=\Vec{r}_2-\Vec{r}_1=\overrightarrow{A_1A_2}\). Takto jednoduše ho budeme vždy konstruovat. Jak uvidíme dále, vektor posunutí je rovnoběžný s vektorem rychlosti.
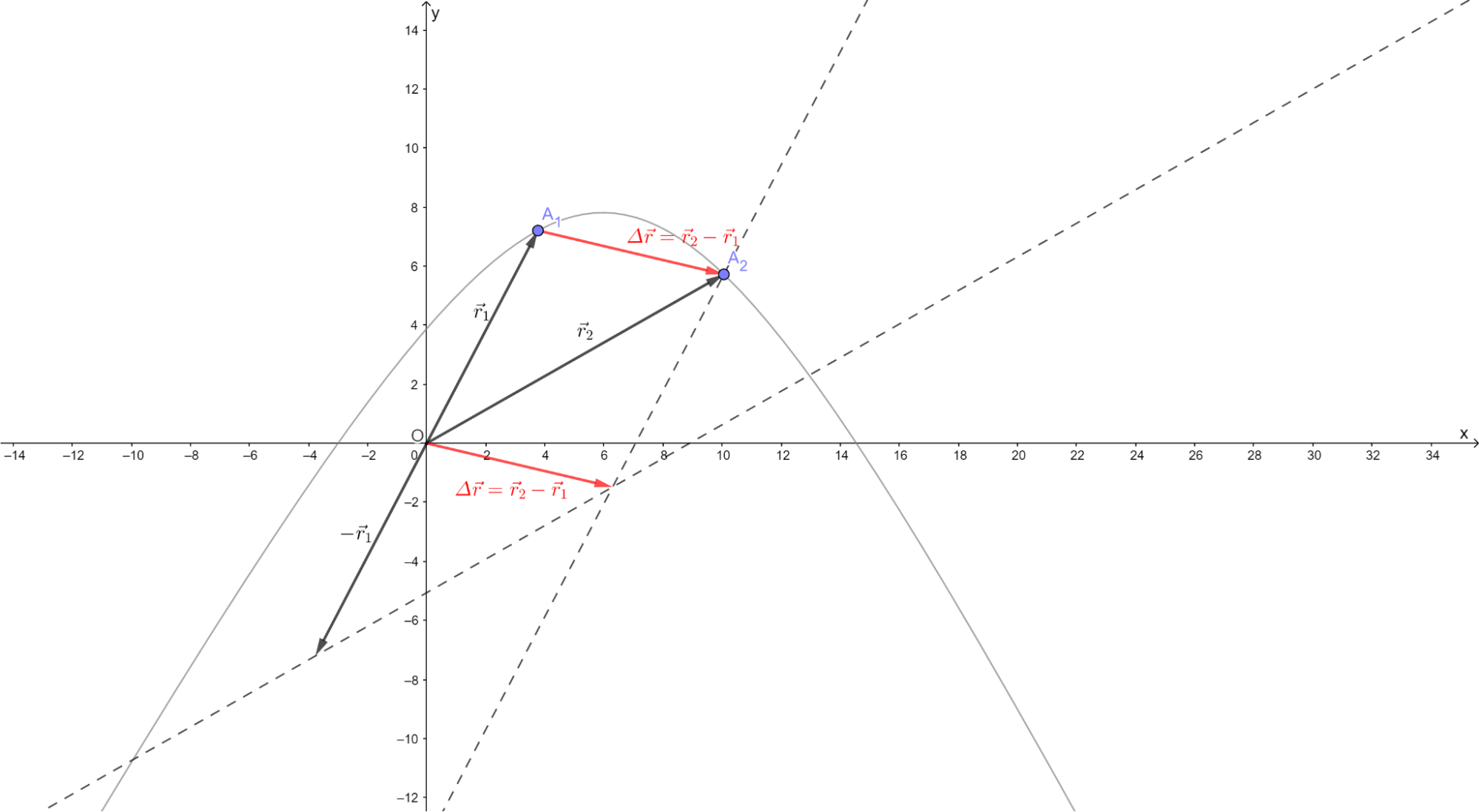
Zdroj
https://www.geogebra.org/classic/rytj5b9q

