Při klidném přímočarém letu v dopravním letadle nemá cestující na palubě žádnou možnost poznat, jakou rychlostí se letadlo právě pohybuje. Může o tom přemýšlet a přitom se procházet tam a zpátky po směru a proti směru letu rychlostí o velikosti 1 m/s. To je jeho rychlost vůči letadlu. Jestliže letadlo letí rychlostí 200 m/s vzhledem k Zemi, asi každý by dokázal říci, že vzhledem k ní bude rychlost pasažéra 199 m/s, nebo 201 m/s podle toho, na kterou stranu půjde. Je-li \(\Vec{v}_A\) rychlost tělesa v soustavě A (rychlost pasažéra vůči letadlu) a \(\Vec{u}\) rychlost pohybu soustavy A vůči soustavě B (rychlost letadla vůči Zemi), pak rychlost tělesa v soustavě B (rychlost pasažéra vůči Zemi) je:
\[ \Vec{v}_B = \Vec{v}_A + \Vec{u} \]Sčítají se vektory, proto v našem případě bude velikost rychlosti \(v_B=(200+1)\ \mathrm{m/s}=201\ \mathrm{m/s}\), nebo \(v_B=(200-1)\ \mathrm{m/s}=199\ \mathrm{m/s}\). Vztah samozřejmě můžeme použít i pro skládání (sčítání) rychlostí libovolného směru. Ukážeme si to v následujících příkladech.
Stíhací letoun Gripen se pohybuje rychlostí o velikosti 410 m/s. Dávka z kanónu vyslaná ve směru letu má úsťovou rychlost 1 025 m/s. Jaká je rychlost střely vzhledem k pozemskému pozorovacímu stanovišti?
Řešení: 1 435 m/s.
Má cenu běžet při dešti?
Určitě jste již někdy museli jít ven za deště a neměli při sobě deštník. Přemýšleli jste někdy nad tím, jestli se vyplatí v dešti běžet, nebo jít normálně? Zmoknete více, nebo méně? (Uvažujte rychlost svého pohybu vzhledem k rychlosti a směru dešťových kapek.)
Zkuste porovnat tyto dvě situace:
- prší šikmo proti směru vašeho pohybu,
- prší šikmo ve směru vašeho pohybu.

Zdroj
1) Jestliže prší proti mně, je nejlepší se pohybovat na dešti co nejkratší dobu, protože na mne zepředu dopadne nejméně kapek.
2) Jestliže naopak prší zezadu, je výhodnější pokusit se srovnat rychlost svého pohybu s vodorovnou rychlostí dešťových kapek. Když bude má rychlost větší než tato složka, budu do kapek „nabíhat“, a budu mokrý i zepředu. Když bude má rychlost menší než vodorovná složka rychlosti dešťových kapek, budu více mokrý zezadu. Jsou-li tyto rychlosti stejné, jediná voda, která mne smočí, dopadá na hlavu. Jak to ale dokázat v praxi a nezmoknout, že?
Dopravní letadlo míří z Londýna do New Yorku. Jeho rychlost je 800 km/h vůči okolnímu vzduchu. Vzhledem k bočnímu větru o rychlosti 120 km/h musí letět s trupem natočeným proti směru proudění větru, aby letělo nejkratší cestou.
- Jaká bude jeho výsledná rychlost pohybu vůči Zemi?
- Za jak dlouho dorazí do cíle své cesty? Vzdálenost mezi zmíněnými městy je 5 560 km. Porovnejte s dobou letu za bezvětří.
- Nejrychlejší let z New Yorku do Londýna trval pouze 4 h 56 min. Bylo to 9. února 2020. Letadlo bylo unášeno tryskovým prouděním zesíleným bouří Sabina. Jaká byla rychlost letadla vůči Zemi? Jaká byla rychlost větru? Předpokládejme, že byla stálá po celou dobu letu.
a) Situace je znázorněna na následujícím obrázku.
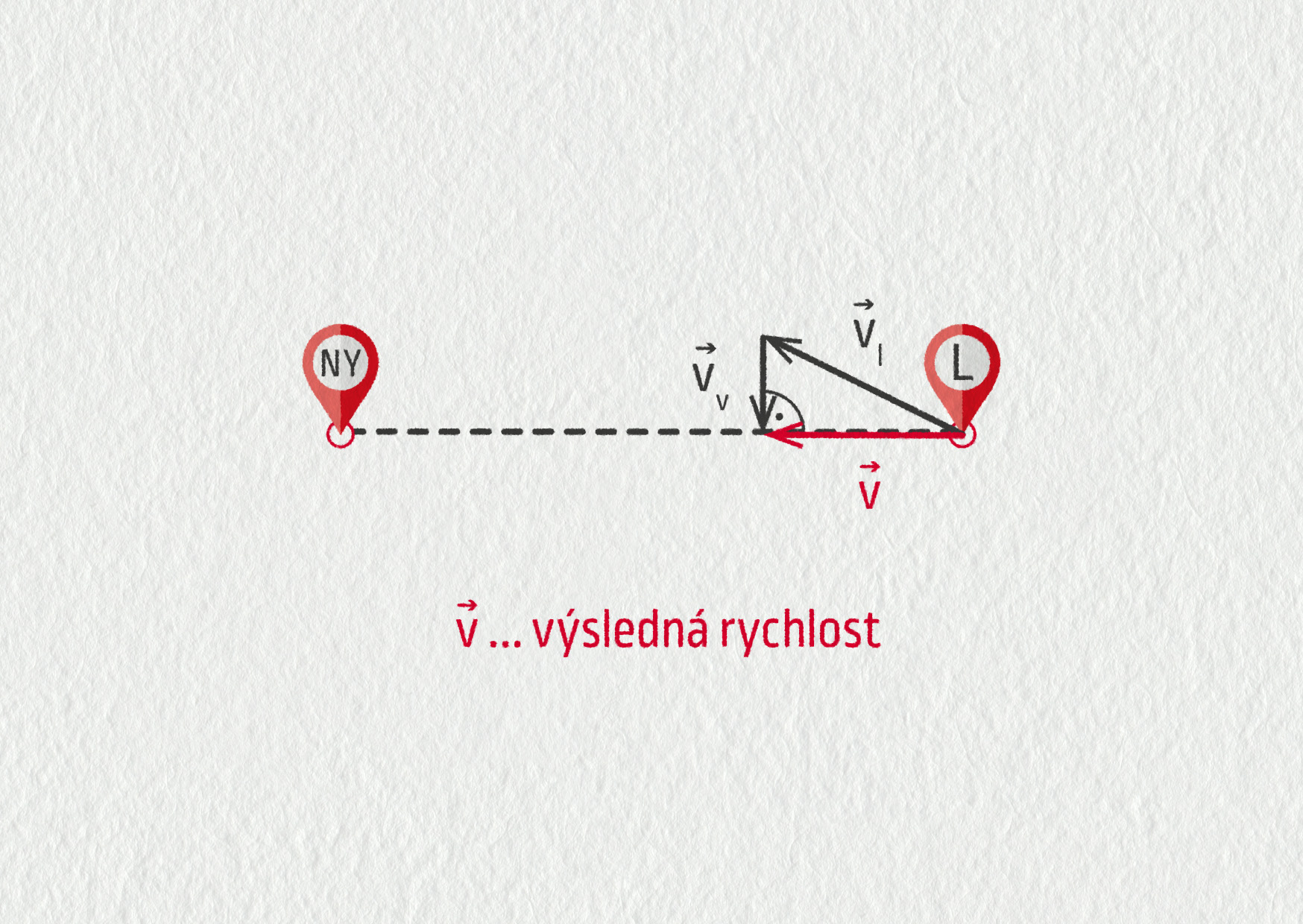
Zdroj
Letadlo musí letět mírně proti větru, aby směr jeho výsledného pohybu odpovídal spojnici mezi Londýnem a New Yorkem. Výsledná rychlost \(\Vec{v}\) je odvěsnou pravoúhlého trojúhelníku. Proto můžeme psát
\[ v = \sqrt{v_{\mathrm l}^2-v_\mathrm{v}^2} = \sqrt{800^2-120^2} = 791\ \mathrm{km/h} \]b) Kdyby byl let přímý, trval by
\[ t_1 = \frac{s}{v_\mathrm{l}} = \frac{5560}{800} = 6{,}96\ \mathrm{h}\;. \]S nižší rychlostí \(v=791\ \mathrm{km/h}\) (bočním vítr) bude let trvat
\[ t_2 = \frac{s}{v} = \frac{5560}{791} = 7{,}03\ \mathrm{h}\;. \]Rozdíl časů tedy je \(\Delta t=t_2-t_1=0{,}08\ \mathrm{h}=5\ \mathrm{min}\).
c) Při rekordním letu z New Yorku do Londýna byla průměrná rychlost letadla
\[ v_\mathrm{r} = \frac{s}{t_\mathrm{r}} = \frac{5560}{4{,}93} = 1128\ \mathrm{km/h}\;. \]Protože letadlo bylo unášeno rychlostí \(v_\mathrm{b}\) ve stejném směru, platí \(v_\mathrm{r}=v_\mathrm{l}+v_\mathrm{b}\). Pro rychlost větru tedy získáme \(v_\mathrm{b}=v_\mathrm{r}-v_\mathrm{l}=1128-800=328\ \mathrm{km/h}\).
Chcete-li si přečíst více:
S lodí přes řeku.

Zdroj
Určitě jste se už někdy pokoušeli přejet s lehkou kanoí přes proudící řeku. I když je proud řeky někdy poměrně slabý, je obtížné udržet loď v pohybu kolmém k proudu. Příď musíme natočit proti směru proudu, abychom vyrovnali proud řeky.
- Pod jakým úhlem je potřeba natočit příď lodě, když voda v řece plyne rychlostí 1,1 m/s a rychlost kanoe vůči klidné vodě je 1,8 m/s?
- Jestliže loď nenatočíme proti proudu a budeme „mířit“ přímo na protější břeh řeky, jak daleko od předpokládaného místa přistání nás proud zanese? Šířka řeky je 18 m.
a) Řešení je zakresleno v následujícím obrázku. Musíme složit vektory rychlosti lodě \(\Vec{v}_\mathrm{k}\) a řeky \(\Vec{v}_\mathrm{r}\).
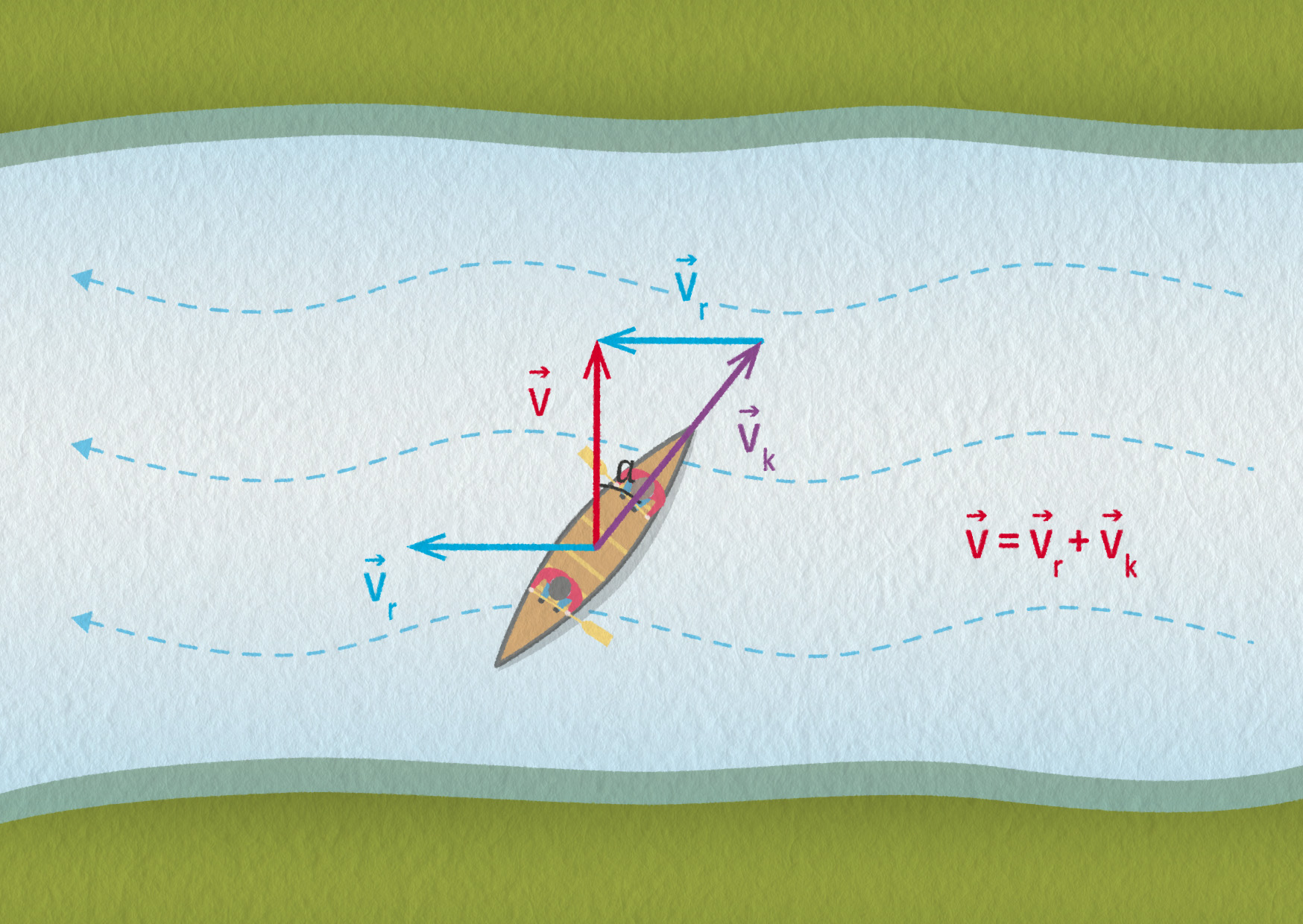
Zdroj
Rychlost kanoe je přeponou v pravoúhlém trojúhelníku a rychlost řeky jeho odvěsnou. Použijeme goniometrické funkce a vypočítáme
\[ \sin\alpha = \frac{v_\mathrm{r}}{v_\mathrm{k}} = \frac{1{,}1}{1{,}8} = 0{,}61\;. \]Pro velikost úhlu pak \(\alpha=38^\circ\).
b) Tentokrát se vektory rychlosti kánoe a řeky složí dle následujícího obrázku.
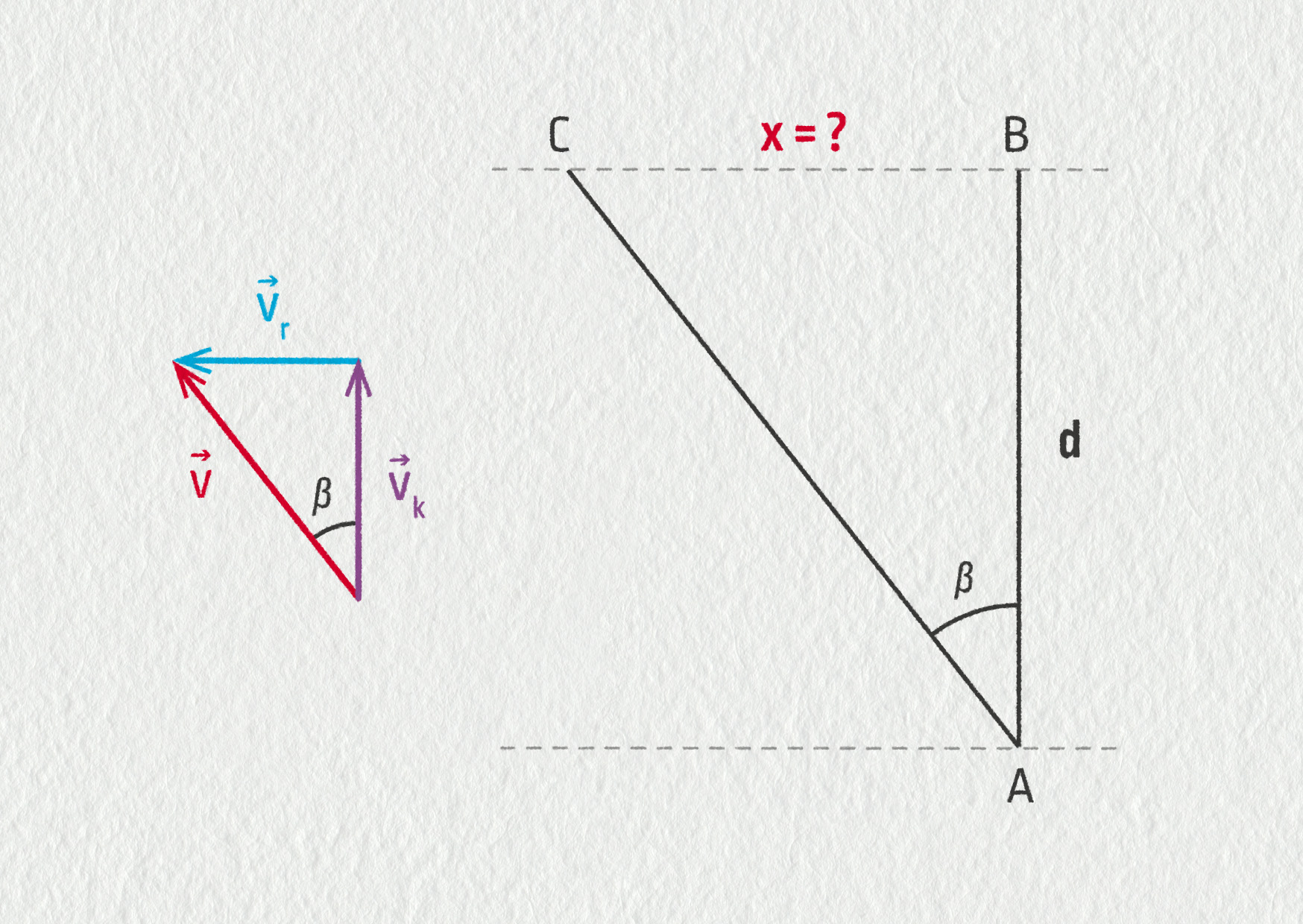
Zdroj
Místo do bodu B, který je přímo na protější straně řeky, nás proud odnese až do bodu C, který je dole po proudu. Z podobnosti obou trojúhelníku můžeme napsat \(v_\mathrm{r}/v_\mathrm{k}=x/d\). Pro vzdálenost \(x\), o kterou nás proud unese, pak vypočteme
\[ x = d\frac{v_\mathrm{r}}{v_\mathrm{k}} = 18\cdot\frac{1{,}1}{1{,}8} = 11\ \mathrm{m} \]Skládání rychlostí, jak jsme ho představili v této kapitole, funguje pouze za podmínky, že rychlost pohybujících se těles není příliš velká. Pokud se totiž tělesa pohybují rychlostmi řádově desetiny rychlosti světla \(( c = 3 \cdot 10^8\ \mathrm{m/s} )\), musíme vzít na pomoc relativistickou kinematiku a začít rychlosti sčítat podstatně jinak.
Pro relativistické skládání rychlostí platí vztah
\[ v_B = \frac{v_A+u}{\displaystyle1+\frac{\strut v_Au}{c^2}}\;. \]V tomto vztahu je opět rychlost \(v_A\) rychlost tělesa vůči soustavě A, rychlost \(u\) je rychlost samotné soustavy A vůči soustavě B a výsledná rychlost \(v_B\) je rychlost tělesa vůči soustavě B.
Podívejme se, že tento na první pohled složitý vztah je v souladu se vztahem pro klasické skládání rychlostí. Zkusme za rychlosti dosadit rychlost pasažéra v letadle \(v_A=1\ \mathrm{m/s}\) a rychlost \(u=200\ \mathrm{m/s}\) za rychlost letadla vůči Zemi. Pro výslednou rychlost pasažéra vůči Zemi pak získáme
\[ v_B = \frac{200+1}{\displaystyle1+\frac{\strut 200\cdot1}{(3\cdot10^8)^2}} \approx 201\ \mathrm{m/s}\;, \]tedy naprosto stejný výsledek jako při klasickém skládání rychlostí.
To proto, že tyto rychlosti jsou oproti rychlosti světla ve vakuu docela zanedbatelné. Ani nejrychlejší člověkem vyrobené vesmírné sondy pohybující se rychlostí například \(200\,000\ \mathrm{km/h}=55{,}6\ \mathrm{km/s}=0{,}00019c\) nedosahují rychlostí, kdy bychom museli tento vztah používat. Relativistický vztah se začíná projevovat až při rychlostech kolem \(0{,}3c\). Zkusíme-li tentokrát dosadit za rychlost \(v_A=0{,}3c\), za rychlost \(u=0{,}3c\), získáme po výpočtu výslednou rychlost
\[ v_B = \frac{0{,}3c+0{,}3c}{\displaystyle1+\frac{\strut (0{,}3c)^2}{c^2}} = \frac{0{,}6c}{1+0{,}09} \approx 0{,}55c\;. \]Výsledná rychlost je tedy poněkud menší než očekávaných \(0{,}6c\) podle klasické kinematiky.
Rychlostí blízkých rychlosti světla ve vakuu dosahují nabité částice, které jsme pomocí elektrického napětí o velikosti desítek milionů voltů urychlili v urychlovačích. Jestliže budeme skládat rychlosti blízké rychlosti světla, vždy dostaneme rychlost, která bude menší než rychlost světla, a nikoliv \(2c\), jak bychom mohli očekávat. Právě fakt, že rychlost světla nemůže žádné těleso překročit, je jedním za základů speciální teorie relativity.

