Rychlost

Ve třetí kapitole jsme zavedli okamžitou rychlost na ose \(x\) jako \(v_x=\Delta x/\Delta t\). Tato definice zahrnuje také informaci o směru pohybu tělesa. Je-li hodnota rychlosti kladná, hmotný bod se pohybuje ve směru dané osy, je-li záporná, hmotný bod se pohybuje proti směru této osy.

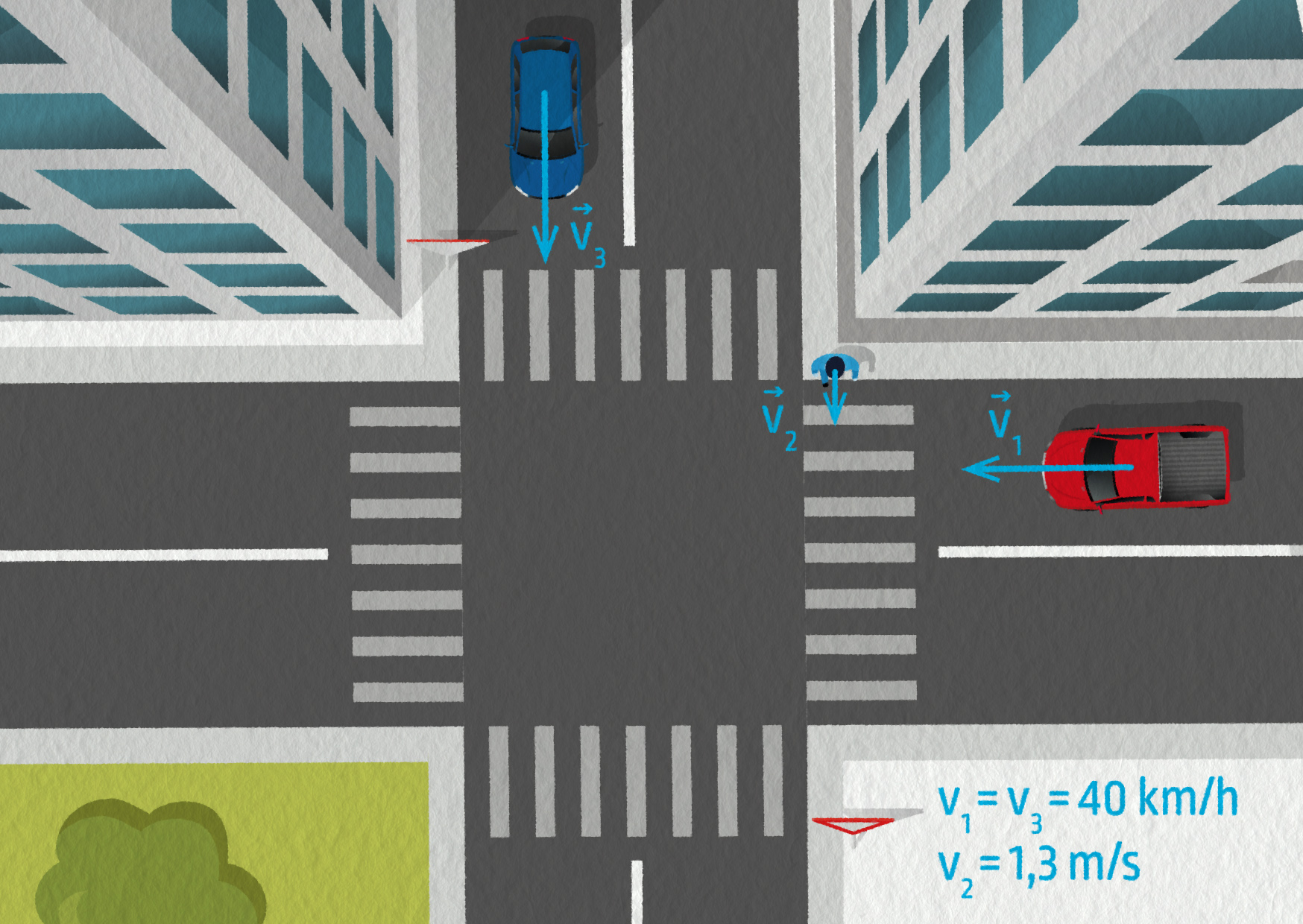
Směr pohybu, a tudíž i rychlosti je velmi důležitý (není jedno, zda jdete do školy, či ze školy :-). Když přecházíme ulici, vždy se pečlivě rozhlédneme a vyhodnotíme, jakým směrem a jakou rychlostí se pohybují projíždějící automobily.

Nikdo nechce, aby vešel do cesty červenému automobilu. Naopak modrý automobil, přestože jede stejně rychle jako červený, nás nijak neohrožuje. Víme totiž, že směr jeho pohybu je rovnoběžný s naším, a trajektorie našich pohybů se ani neprotnou.

Rychlost je vektorová veličina – hovoříme o vektoru rychlosti \(\Vec{v}\) a můžeme ji snadno definovat pomocí vektoru posunutí.

Okamžitá rychlost má vždy směr tečny k trajektorii. Dobrou představu o směru okamžité rychlosti si můžete udělat na následující animaci. Ukazuje směr vektoru posunutí. Když přiblížíme body M₁ a M₂ blízko k sobě, ze sečny k trajektorii se stává tečna a to je také směr vektoru okamžité rychlosti v bodě M.

Animace v Geogebře: https://www.geogebra.org/calculator/ked53gkn

Rychlost \(\Vec{v}\) podle definice můžeme rozepsat do složek takto:

Příklad 1

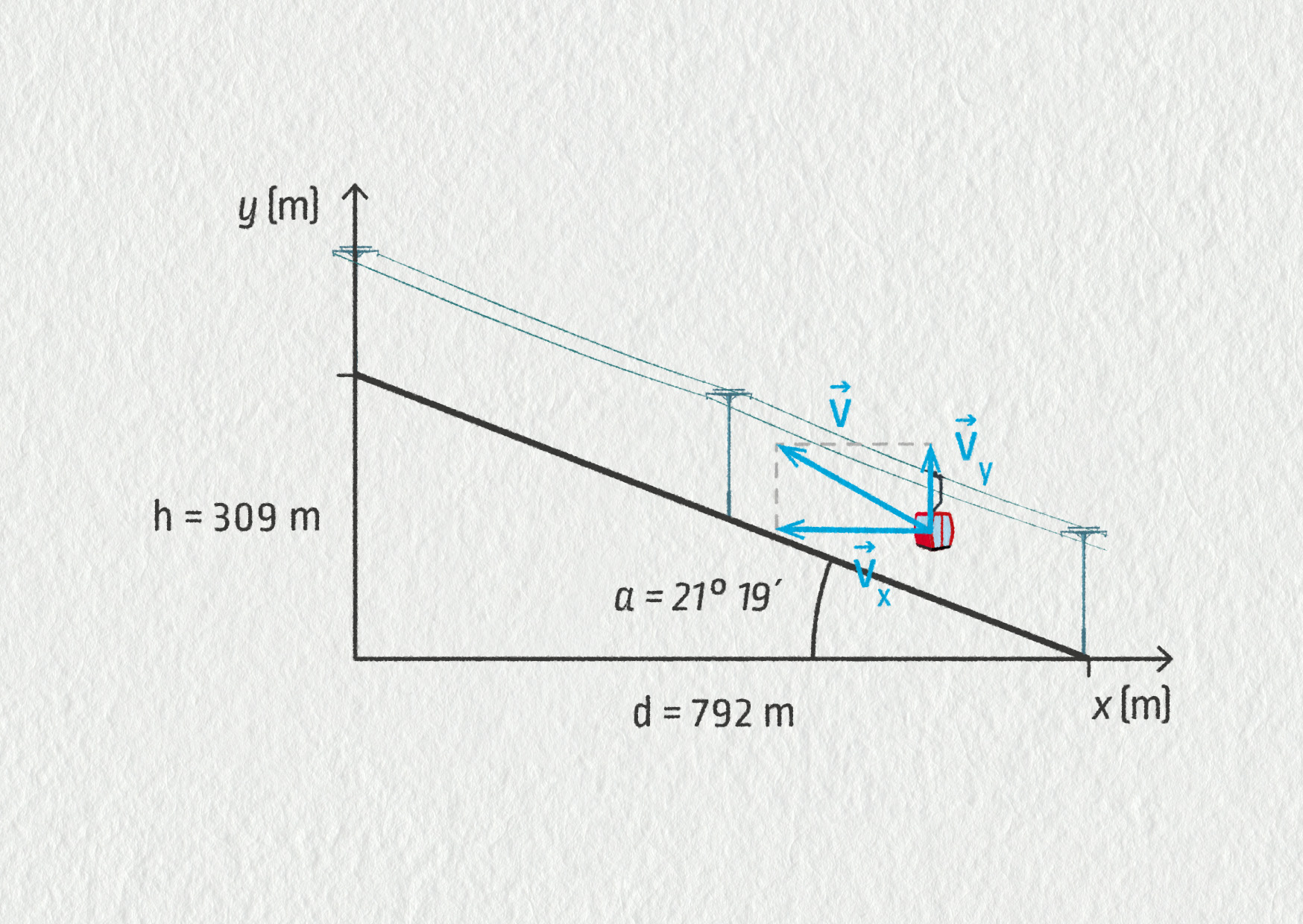
Kabinka lanovky na obrázku se pohybuje rychlostí o velikosti 2,9 m/s. Na přímém úseku vystoupá o 309 m na vodorovné vzdálenosti 792 m. Určete složky rychlosti kabinky. Jak dlouho bude lanovce trvat, než překoná celkový výškový rozdíl mezi stanicemi, který činí 822 m?

Řešení:

Převýšení 309 m na vodorovné vzdálenosti 792 m odpovídá pravoúhlému trojúhelníku s úhlem α o velikosti 21° 19′ při delší odvěsně.

Pro rychlost a její složky tedy platí: \(\sin\alpha=v_y/v\), \(\cos\alpha=-v_x/v\). Odtud pak získáme

\[ \begin{aligned} v_x &= -v\cos\alpha = -2{,}9\cdot\cos(21^\circ\,19') = -2{,}7\ \mathrm{m\cdot s}^{-1}\\ v_y &= v\sin\alpha = 2{,}9\cdot\sin(21^\circ\,19') = 1{,}1\ \mathrm{m\cdot s}^{-1}\\ \end{aligned} \]

Při vertikální rychlosti o velikosti \(v_y=1{,}1\ \mathrm{m/s}\) lanovka překoná výšku mezi stanicemi za

\[ t = \frac{h}{v_y} = \frac{822\ \mathrm{m}}{1{,}1\ \mathrm{m/s}} = 747\ \mathrm{s}\;. \]

V angličtině narazíte na dva pojmy: speed a velocity. První z nich označuje velikost rychlosti tělesa. Například na tachometru (anglicky speedometer) vidíte 75 mph (přibližně 120 km/h). Víme, jak rychle se pohybujeme, ale vůbec nevíme, jakým směrem.

Na dalším obrázku vidíme několik automobilů. Řekněme, že osobní automobily mají rychlost o velikosti 120 km/h (tedy speed). Jejich „velocity“ jsou však různé. Pohybují se ve dvou různých směrech. V češtině máme jen jedno slovo – rychlost. Z kontextu musíme poznat, jestli máme na mysli vektorovou veličinu rychlost (velocity), nebo jen velikost rychlosti (speed).

14.27 – Znázornění rychlosti automobilu.
Zdroj

Příklad 2

Vraťme se ještě jednou k pohybu vlaku mezi stanicemi Velim a Pečky.

Zjistili jsme, že posunutí \(\Delta\Vec{r} = (-7000\ \mathrm{m};2500\ \mathrm{m})\). Vlak vyjíždí z Velimi v 10:08 a zastavuje v Pečkách v 10:24. Jeden čtvereček na mapě znázorňuje plochu 1000x1000 m.

Určete průměrnou rychlost vlaku mezi stanicemi a také její velikost.

Řešení:

Doba pohybu je \(\Delta t=t_2-t_1=16\ \mathrm{minut}=960\ \mathrm{s}\).

Průměrná rychlost je vyjádřena vztahem \(\Vec{v}=\Delta\Vec{r}/\Delta t\). Rychlost \(\Vec{v}\) má složky

\[ \begin{aligned} v_x &= \frac{\Delta x}{\Delta t} = \frac{-7000}{960} = -7{,}3\ \mathrm{m\cdot s}^{-1} \\ v_y &= \frac{\Delta y}{\Delta t} = \frac{2500}{960} = 2{,}6\ \mathrm{m\cdot s}^{-1} \\ \end{aligned} \]

Rychlost \(\Vec{v}\) zapíšeme \(\Vec{v}=(-7{,}3; 2{,}6)\ \mathrm{m\cdot s}^{-1}\).

Velikost vektoru získáme z Pythagorovy věty

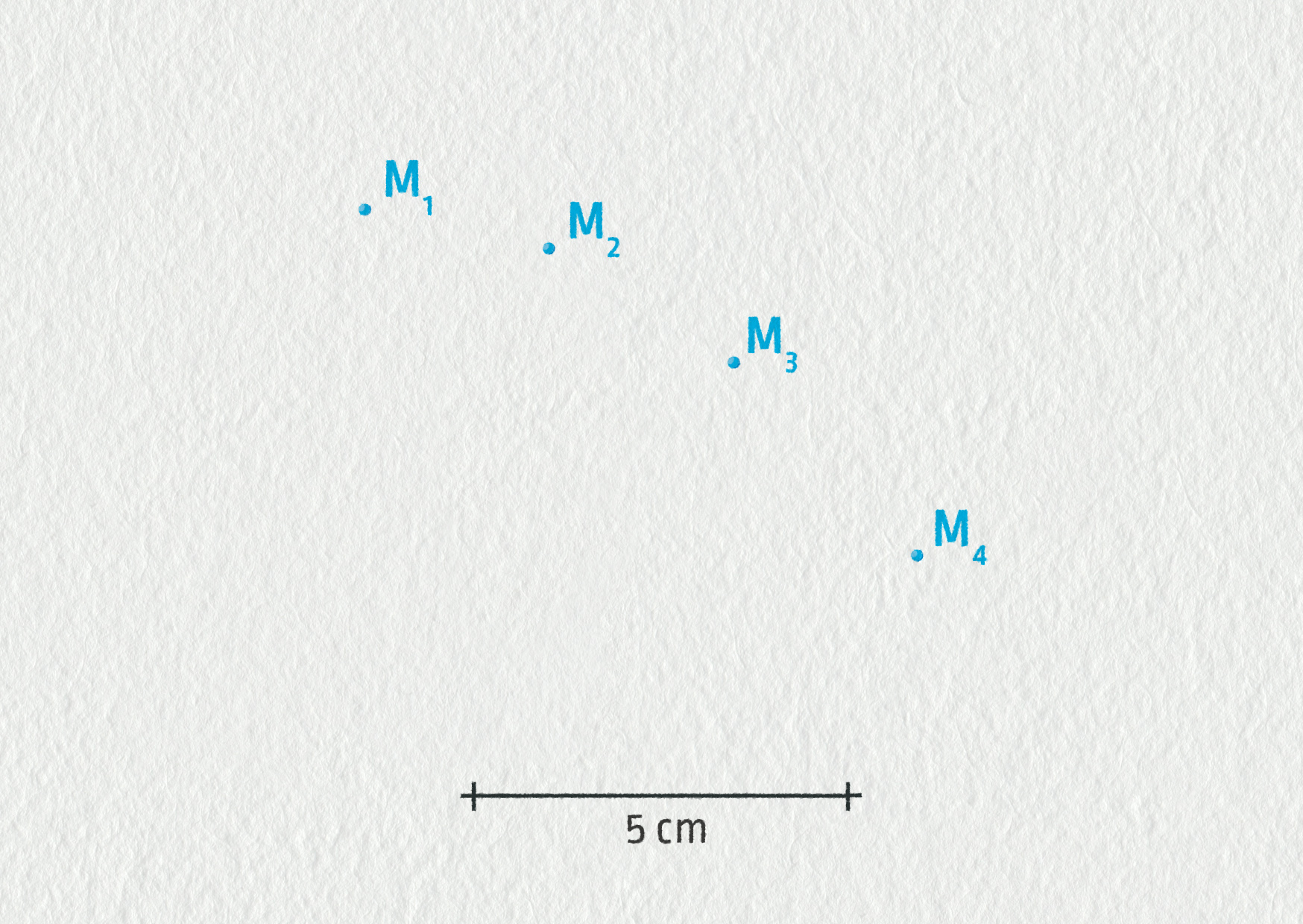
\[ v=\sqrt{v_x^2+v_y^2}=\sqrt{7{,}3^2+2{,}6^2}=7{,}7\ \mathrm{m\cdot s}^{-1}\;. \]

Příklad 3

Na následujícím obrázku jsou znázorněny čtyři po sobě jdoucí polohy pohybujícího se tělesa. Doba, která uplynula mezi dvěma po sobě jdoucími pozicemi, je \(\tau=25\ \mathrm{ms}\). Určete velikost rychlosti tělesa v bodě M₂. Rychlost \(\Vec{v}_2\) zakreslete do obrázku. Doporučené měřítko: \(1\ \mathrm{cm}\sim25\ \mathrm{cm\cdot s}^{-1}\) (PDF ke stažení).

Řešení:

Naše řešení nemůže být zcela přesné, musíme vycházet z naměřených bodů. Pro výpočet okamžité rychlosti v určitém bodě si vybereme nejmenší možné okolí tohoto bodu. Jestliže tedy určujeme rychlost v bodě M₂ dle zadání, volíme nejbližší předcházející a následující bod (M₁ a M₃).

Podle definice \(\Vec{v}=\Delta\Vec{r}/\Delta t\), kde \(\Vec{r}=\overrightarrow{M_1M_3}\) a \(\Delta t=2\tau\). Vzdálenost M₁M₃ změříme v záznamu a pro velikost rychlosti dostáváme

\[ v_2 = \frac{|M_1M_3|}{2\tau} = \frac{5{,}2\ \mathrm{cm}}{2\cdot0{,}025\ \mathrm{s}} = 104\ \mathrm{cm\cdot s}^{-1} \]

Z definice plyne i směr rychlosti: \(\Vec{v}_2\) je rovnoběžná s vektorem \(\overrightarrow{M_1M_3}\). Zvolíme-li měřítko \(1\ \mathrm{cm}\sim25\ \mathrm{cm\cdot s}^{-1}\), do bodu M₂ narýsujeme vektor o délce 4,2 cm.

Celou konstrukci si můžete zobrazit zde https://www.geogebra.org/calculator/ka87eswm.