Čím je tvořena vnitřní energie tělesa?

Zdroj
S chaotickým pohybem částic v tělese je spojena značná kinetická energie. Tato energie je „ukryta“ uvnitř tělesa, proto ji označujeme jako vnitřní kinetickou energii. Nabízí se otázka – může mít těleso také vnitřní potenciální energii? Ano, může, protože atomy na sebe vzájemně působí silami, mohou navazovat vazby (spojovat se do molekul), nebo se vazby mohou naopak štěpit. To se děje při změnách skupenství nebo v chemických reakcích. Například při vypařování je potřeba dodat energii k přerušení vazeb mezi molekulami. Nebo při hoření dochází k uvolňování vazebné energie. Naopak vaše tělo si dokáže ukládat vnitřní potenciální energii ve formě cukrů a tuků. Obrovská potenciální energie je spojena také s jadernými silami. Změny jaderné energie nastávají při jaderných reakcích, které jsou však, narozdíl od chemických reakcí, v našem okolí docela vzácné.
Vnitřní energie = vnitřní kinetická energie (energie chaotického pohybu částic) + vnitřní potenciální energie (chemická, jaderná)
Podívejme se na vazebnou energii ještě trochu podrobněji. Z chemie víme, že u některých reakcí se potenciální energie vazeb snižuje a látka se ohřívá – takovým reakcím říkáme exotermické. Naopak pokud se potenciální energie vazeb zvyšuje, mluvíme o endotermických reakcích. Detaily si ukážeme na konkrétním příkladu hoření plynu.
Zemní plyn, který používáme k topení a vaření, je z velké části tvořen metanem. Dokonalé spalování metanu je možné popsat jednoduchou chemickou rovnicí, a to včetně uvolněné vazebné energie.
\[\mathrm{CH}_4 + 2\mathrm{O}_2 \to \mathrm{CO}_2 + 2\mathrm{H}_2\mathrm{O}\ ({}+1{,}32\cdot10^{-18}\ \mathrm{J})\]Jak si to představit? Přeskupením atomů při reakci se vnitřní potenciální energie sníží (navážou se pevnější vazby mezi atomy) a o stejný díl vzroste vnitřní kinetická energie (látka se ohřeje). Uvolněná energie je číselně velmi malá, ale to proto, že je vztažena jen k jedné molekule metanu. Můžeme ji přepočítat na větší množství látky, jak ukazuje následující příklad.
Pomocí výše uvedené rovnice vypočítejte, kolik energie se uvolní dokonalým spálením 1 kg metanu. Molární hmotnost metanu je \(M_\mathrm{m}=16\ \mathrm{g}/\mathrm{mol}\).
Úlohu budeme řešit obecně, číselné dosazení necháme až na konec. Snadno spočítáme, kolik energie se uvolní spálením 1 molu metanu:
\(E_\mathrm{mol} = N_\mathrm{A} E_1\) (\(E_1\) je energie uvolněná spálením 1 molekuly metanu, \(N_\mathrm{A} \) je Avogadrova konstanta)
Dál musíme vypočítat, kolik molů je v 1 kg metanu. Ale to už umíme:
\[ n = \frac{m}{M_\mathrm{m}} \]Dohromady:
\[ E = n E_\mathrm{mol} = \frac{m}{M_\mathrm{m}}\cdot N_\mathrm{A} E_1 = 50\,000\,000\ \mathrm{J} = 50\ \mathrm{MJ} \]Energie uvolněná při chemické reakci má velký praktický význam. Pomocí ní je definována výhřevnost \(H\) – množství energie, která se uvolní dokonalým spálením 1 kg paliva. Platí:
\[ H = \frac{E}{m} \]| Látka | Výhřevnost v MJ/kg |
|---|---|
| vodík | 120 |
| metan | 50 |
| benzín | 44 |
| nafta | 43 |
| černé uhlí | cca 30 |
| dřevo | cca 15 |
V tabulce vidíme jasného vítěze v množství energie na jednotku hmotnosti – vodík. Proto se používá třeba jako palivo v raketových motorech. Problém vodíku je ale ten, že se velmi špatně skladuje a má malou hustotu. Pro zajímavost uveďme, že hustota energie lithiového akumulátoru je cca 0,7 MJ/kg (hustota energie akumulátoru je údaj srovnatelný s výhřevností – udává množství elektrické energie uložené v 1 kg). Tento fakt může za to, že většina aut stále ještě jezdí na benzín či naftu, kde je množství energie uložené v jednom kg o dva řády vyšší.
V předchozích příkladech jsme počítali výhřevnost – energii uvolněnou dokonalým spálením 1 kg látky. Často se ale stává, že hořením vzniká voda, která poté může kondenzovat. Při změně skupenství z plynu na kapalinu se uvolní ještě další energie (skupenské teplo). Proto se definuje veličina spalné teplo – energie, která se uvolní při spálení 1 kg látky za předpokladu, že voda uvolněná spalováním zkondenzuje. Tím se spalné teplo liší od výhřevnosti, kde je na konci reakce voda v plynném skupenství. Spalné teplo je tedy větší o skupenské teplo vypařování vody. Rovnost nastává jen v případech, kdy spalováním nevzniká voda.
Petr se rozhoduje, zda topit plynem, dřevem či elektřinou. Plyn nakupuje za cenu 13 Kč za m3 plynu. Z 1 m3 plynu získáme asi 10,5 kWh energie. Pro krbová kamna má k dispozici smrkové dřevo za cenu 550 Kč/m3. Elektřinu pro vytápění může nakupovat za cenu 2 Kč/kWh. Porovnejte cenu za kWh pro všechny tři způsoby vytápění.
Plyn: cena za 1 kWh je \(13\ \hbox{Kč}/10{,}55\ \mathrm{kWh} = 1{,}2 \hbox{Kč}/\mathrm{kWh}\)
Dřevo: nejprve vyhledáme hustotu smrkového dřeva (450 kg/m3) a jeho výhřevnost (15 MJ/kg). Výhřevnost snadno převedeme: \(15\ \mathrm{MJ/kg}\cdot450\ \mathrm{kg}/\mathrm{m}^3 = 6750\ \mathrm{MJ}/\mathrm{m}^3\). Cena za 1 MJ je tedy \(550\ \hbox{Kč}/6750\ \mathrm{MJ}=0{,}08\ \hbox{Kč}/\mathrm{MJ}\). \(1\ \mathrm{kWh}=3{,}6\ \mathrm{MJ}\), proto \(0{,}08\ \hbox{Kč}/\mathrm{MJ} = 0{,}29\ \hbox{Kč}/\mathrm{kWh}\).
Vidíme, že dřevo jasně vede, na druhém místě je plyn a poslední elektřina. Cena za kWh však není jediný faktor při výběru zdroje tepla. Zkuste sami jmenovat některé další.
Teplo

Zdroj
Představte si, že chcete uvařit čaj. Můžete k tomu použít oheň, plynový sporák nebo rychlovarnou konvici. Ve všech případech ohříváte vodu díky tomu, že ji necháte v kontaktu s horkým tělesem. Částice horkého tělesa se pohybují většími rychlostmi a při nárazech předávají energii pomalejším částicím studenější látky. Tomuto způsobu předávání vnitřní energie říkáme tepelná výměna. Z toho vyplývá definice tepla jako samostatné fyzikální veličiny. Teplo \(Q\) je vnitřní energie předaná mezi tělesy v důsledku jejich teplotního rozdílu.
Jak ale zjistíme, jaké teplo je potřeba k ohřátí daného tělesa? Odpověď je možné získat experimentálně. Například ohříváním látek pomocí elektrického proudu. Dodané teplo je v tomto případě rovno spotřebované elektrické energii (\(Q=E=UIt\)).
Chcete-li provést vlastní měření, které alespoň přibližně prokáže, jak souvisí změna teploty tělesa a dodané teplo, bude vám k tomu stačit rychlovarná konvice. Stačí znát výkon konve \(P\) a měřit čas ohřevu \(t\). Pak platí \(E=Pt\). Takto vypočítanou energii můžeme porovnávat s tím, kolik vody (hmotnost \(m\)) a o jaký teplotní rozdíl (\(\Delta t\)) jsme ohřáli. Připravte si podobnou tabulku, jako je na obrázku, a pusťte se do vlastního měření.
Na základě vašeho měření odpovězte na otázky.
- Jaká je závislost dodané energie na teplotním rozdílu?
- Jaká je závislost dodané energie na hmotnosti vody?
- Pokuste se na základě změřených dat vypočítat, kolik energie by bylo potřeba na ohřátí 1 kg vody o 1 °C.
- Které jevy nejvíc ovlivňují přesnost našeho měření?
| Číslo měření | \(E=Pt\) (J) | \(m\) (kg) | \(\Delta t\) (°C) | Pozn. |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 |
Teplo \(Q\) potřebné k ohřátí homogenního tělesa o teplotní rozdíl \(\Delta T\) je přímo úměrné tomuto teplotnímu rozdílu a hmotnosti tělesa \(m\). Jako konstanta úměrnosti zde vystupuje vlastnost ohřívané látky, která se nazývá měrná tepelná kapacita \(c\).
\(Q = mc\cdot\Delta T\)
\(m\) = hmotnost
\(\Delta T\) = teplotní rozdíl
\(c\) = měrná tepelná kapacita (vlastnost látky)
Připomeňme, že teplotní rozdíl je možné počítat také ve °C, neboť platí \(\Delta T = \Delta t\). Podívejme se nyní blíže na měrnou tepelnou kapacitu. Ze vzorce vyplývá, že jednotkou \(c\) musí být J ⋅ kg−1 ⋅ K−1. Hodnota \(c\) nám tedy říká, kolik tepla je potřeba k ohřátí 1 kg látky o 1 K. Někdy se setkáme ještě s veličinou tepelná kapacita C, která se vztahuje ke konkrétnímu tělesu.
| měrná tepelná kapacita | \(c\) | vlastnost látky | J ⋅ kg−1 ⋅ K−1 |
| tepelná kapacita | \(C=mc\) | vlastnost tělesa | J ⋅ K−1 |
Měrné tepelné kapacity vybraných látek uvádí následující tabulka. Hodnoty \(c\) jsou zjišťovány většinou experimentálně, jejich teoretický výpočet je možný, ale obtížný. Při přesnějších měřeních se také ukazuje, že hodnota \(c\) se může s teplotou mírně měnit, proto jsou běžně uváděné hodnoty platné zpravidla pro teploty kolem 20 °C.
| Látka | Měrná tepelná kapacita v J · kg−1 · K−1 |
|---|---|
| voda | 4 180 |
| ethanol | 2 430 |
| led | 2 050 |
| hliník | 896 |
| železo | 450 |
| měď | 383 |
| vzduch (záleží na podmínkách) | cca 1000 |
Tepelná kapacita nerezového hrnce je 800 J ⋅ K−1. Kolik tepla v joulech je potřeba k ohřátí hrnce o 10 °C?
Potřebujeme přivést 2 l vody k varu z původní teploty 20 °C pomocí rychlovarné konvice.
- Kolik tepla v joulech bude potřeba? Ztráty tepla do okolí neuvažujte.
- Jaká bude cena energie potřebné k ohřevu? Cena elektrické energie je 10 Kč/kWh.
a) Nejdříve vypočítáme potřebné teplo:
\[Q = mc\cdot\Delta T = 2\ \mathrm{kg} \cdot 4180\ \mathrm{J/(kg\cdotK)} \cdot 80\ \mathrm{K} = 668\,800\ \mathrm{J} = 0{,}186\ \mathrm{kWh} \]b) \(668\,800 \mathrm{J} = 0{,}186\ \mathrm{kWh}\). Cena je \(0{,}186\ \mathrm{kWh}\cdot10\ \hbox{Kč/kWh} = 0{,}9\ \hbox{Kč}\).
První dům má mohutné zdi z plných cihel. V druhém jsou použity naopak lehké materiály – dřevo a sádrokarton. Porovnejte chování obou domů z hlediska vnitřní teploty v zimní a letní sezóně.
Cihlové zdi mají velkou hmotnost, a tedy i velkou tepelnou kapacitu. Proto budou stabilizovat teplotu v domě. V zimě bude déle trvat, než se dům ohřeje topením. To může být nevýhodné, pokud není dům trvale obývaný. V horkých dnech se bude v domě udržovat nižší teplota a nebude nutná klimatizace.
Naopak dům z lehkých materiálů se bude rychle ohřívat i chladnout. Teplota uvnitř bude rychleji následovat vnější teploty, což je nevýhodné zejména v létě.
Už víme, že teplo představuje předanou vnitřní kinetickou energii, která je zase spojena s pohybem částic. Proto můžeme teplo počítat ve stejných jednotkách jako mechanickou energii – v joulech. Jméno této jednotce propůjčil anglický fyzik James Prescott Joule na konci 19. století. Předtím se teplo měřilo v samostatných jednotkách – kaloriích. Přestože nejde o povolenou jednotku soustavy SI, občas se s ní setkáte. Jedna kalorie je definována (přibližně) jako teplo potřebné k ohřátí 1 gramu vody o 1 °C. Proto platí: 1 cal = 4,2 J. Více o souvislosti tepla a práce se dočtete v kapitole 12.
Teď ještě vyřešíme jeden důležitý příklad. Probíhá-li tepelná výměna pouze mezi dvěma tělesy (neuvažujeme vliv okolí), teplo odevzdané teplejším tělesem je stejně velké jako teplo přijaté chladnějším tělesem. Zároveň víme, že výsledná teplota obou těles v rovnovážném stavu musí být shodná.
Při přípravě čaje nalijeme 2,0 dl vařící vody do keramického hrníčku o hmotnosti 140 g s měrnou tepelnou kapacitou 960 J ⋅ kg−1 ⋅ K−1. Jaká bude výsledná teplota? Ztráty tepla do okolí neuvažujte.
V zadání úlohy nemáme přesné informace o počáteční teplotě vody a hrníčku. Úlohu proto můžeme vyřešit pouze přibližně. Odhadneme, že vařící voda měla \(t_\mathrm{V}= 100\ ^\circ\mathrm{C}\), zatímco hrníček měl pokojovou teplotu cca \(t_\mathrm{H}=20\ ^\circ\mathrm{C}\). Výslednou teplotu označíme \(t\), hmotnost hrníčku \(m_\mathrm{H}=0{,}14\ \mathrm{kg}\) a hmotnost vody \(m_\mathrm{V}=0{,}2\ \mathrm{kg}\). Voda odevzdává teplo hrníčku, což můžeme zapsat rovnicí \(Q_\mathrm{V} = Q_\mathrm{H}\) (budeme uvažovat obě tepla s kladným znaménkem).
\[m_\mathrm{V}c_\mathrm{V}(t_\mathrm{V}-t) = m_\mathrm{H}c_\mathrm{H}(t-t_\mathrm{H})\]Neznámá \(t\) je v rovnici dvakrát, proto je třeba roznásobit závorky a dál postupovat v úpravě rovnice
\[ \begin{aligned} m_\mathrm{V}c_\mathrm{V}t_\mathrm{V} - m_\mathrm{V}c_\mathrm{V}t &= m_\mathrm{H}c_\mathrm{H}t - m_\mathrm{H}c_\mathrm{H}t_\mathrm{H}\\ m_\mathrm{V}c_\mathrm{V}t_\mathrm{V} + m_\mathrm{H}c_\mathrm{H}t_\mathrm{H} &= m_\mathrm{H}c_\mathrm{H}t + m_\mathrm{V}c_\mathrm{V}t\\ m_\mathrm{V}c_\mathrm{V}t_\mathrm{V} + m_\mathrm{H}c_\mathrm{H}t_\mathrm{H} &= (m_\mathrm{H}c_\mathrm{H} + m_\mathrm{V}c_\mathrm{V})t\\ t &= \frac{m_\mathrm{V}c_\mathrm{V}t_\mathrm{V} + m_\mathrm{H}c_\mathrm{H}t_\mathrm{H}}{m_\mathrm{V}c_\mathrm{V}+m_\mathrm{H}c_\mathrm{H}}\\ \end{aligned} \]V tomto místě je možné udělat rozměrovou zkoušku. Nakonec můžeme dosadit číselné hodnoty a vyjde nám \(t=89\ ^\circ\mathrm{C}\).
Ve vaně je 60 litrů vody o teplotě 45 °C. Kolik litrů studené vody o teplotě 12 °C musíme přilít, abychom dosáhli výsledné teploty 38 °C? Ztráty tepla do okolí neuvažujte.
Jako neznámá zde vystupuje hmotnost studené vody \(m_\mathrm{S}\) o známé teplotě \(t_\mathrm{S}=12\ ^\circ\mathrm{C}\). Horké vody je \(m_\mathrm{H}=60\ \mathrm{kg}\) a má teplotu \(t_\mathrm{H}=45\ ^\circ\mathrm{C}\). Výsledná teplota je \(t=38\ ^\circ\mathrm{C}\). Odevzdané teplo se rovná přijatému: \(Q_\mathrm{H}=Q_\mathrm{S}\) (budeme uvažovat obě tepla s kladným znaménkem).
\[ m_\mathrm{H}c(t_\mathrm{H} - t) = m_\mathrm{S}c(t-t_\mathrm{S}) \]Odtud
\[ m_\mathrm{S} = \frac{m_\mathrm{H}(t_\mathrm{H}-t)}{t-t_\mathrm{S}} \]V tomto místě je možné udělat rozměrovou zkoušku. Nakonec můžeme dosadit číselné hodnoty a vyjde nám \(m_\mathrm{S}=16\ \mathrm{kg}\). Musíme přilít cca 16 l studené vody.
Mechanismy přenosu vnitřní energie
Pokud se teplé těleso dotýká studeného, dochází k přenosu tepla díky nárazům částic – tento proces nazýváme vedení tepla. Teplo je ale možné předávat i na dálku – prostřednictvím elektromagnetického záření. Díky tomu může například Slunce ohřívat Zemi, přestože je odděluje 150 milionů kilometrů prázdného prostoru. V přírodě i v technice má velký význam ještě jeden způsob ohřívání či chlazení těles a tím je proudění. Při proudění se energie transportuje spolu s látkou, například horká voda z kotle přináší teplo potrubím do radiátoru v místnosti. Pojďme se na jednotlivé mechanismy podívat podrobněji.
Vedení tepla
Vedení tepla je prakticky důležité u pevných látek, neboť v kapalinách a plynech má větší význam proudění. Látky, které dobře vedou teplo, se nazývají tepelné vodiče a jsou to zejména kovy. Naopak látky se špatnou tepelnou vodivostí se nazývají tepelné izolanty a jsou to především plyny (kvůli velkým vzdálenostem mezi částicemi). Dokonalý tepelný izolant je vakuum. Aby látka mohla prakticky sloužit jako tepelný izolant, musíme plynu zabránit v proudění. Proto se jako tepelné izolanty používají porézní materiály s velkým obsahem vzduchu uzavřeného v malých oblastech (peří, vata, dřevo, pěnový polystyren…).
Vedení tepla můžeme popsat také kvantitativně. Představme si desku plochy \(S\) a tloušťky \(d\), kdy na opačných koncích desky je udržován teplotní rozdíl \(\Delta T\) (viz obrázek). Pak za čas \(t\) projde deskou teplo
\[ Q = \frac{\lambda \cdot S \cdot t \cdot \Delta T}{d} \]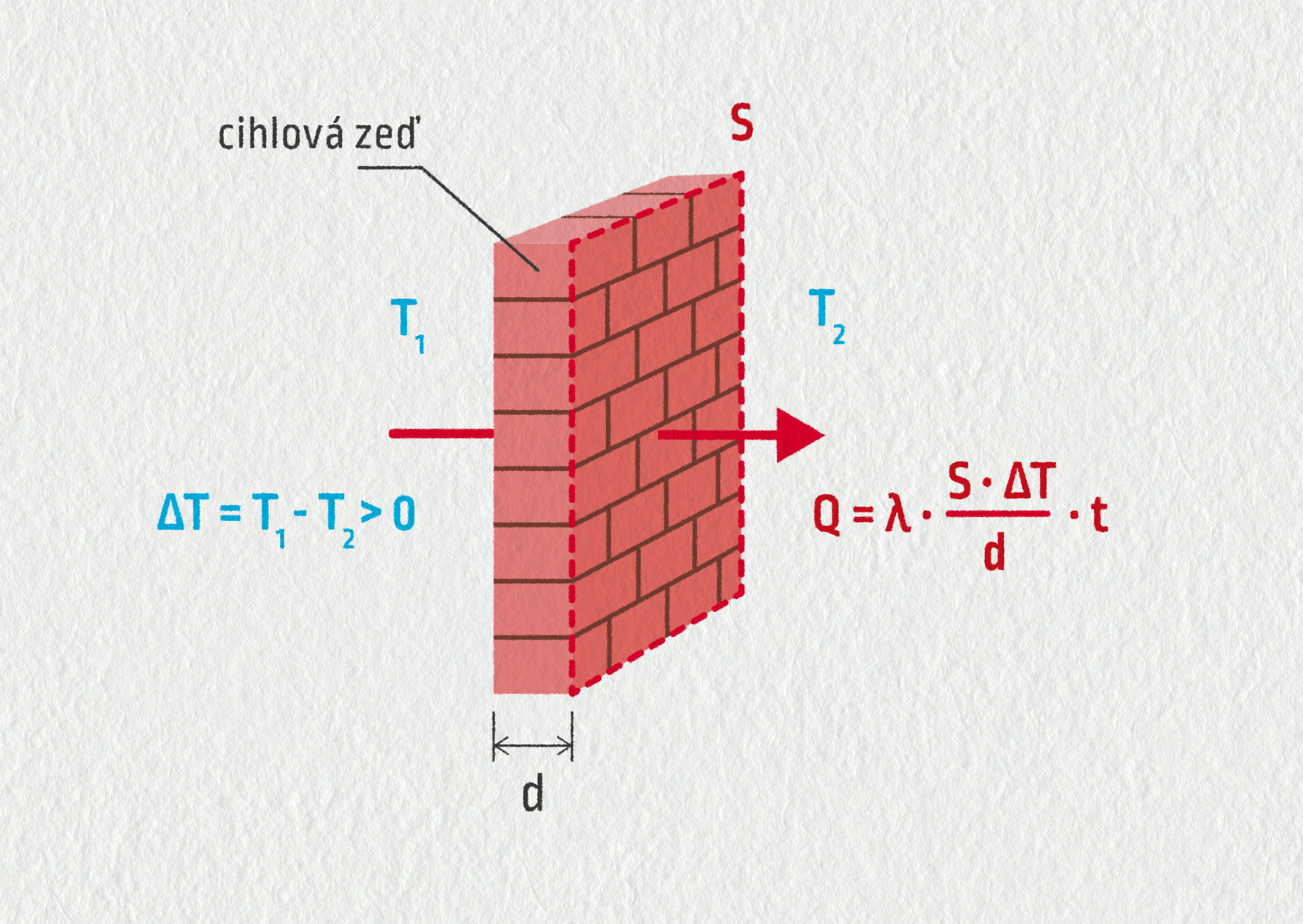
Zdroj
Zkušeného fyzika nepřekvapí, že konstanta úměrnosti \(\lambda\) je vlastnost materiálu. Nazývá se koeficient tepelné vodivosti s jednotkou W ⋅ m−1 ⋅ K−1.
| Látka | Koeficient tepelné vodivosti v W ⋅ m−1 · K−1 |
|---|---|
| měď | 400 |
| hliník | 240 |
| železo | 80 |
| beton | 1,2–1,7 |
| plná cihla | 0,7–0,9 |
| dřevo | 0,1–0,5 |
| minerální vata | cca 0,04 |
Tepelná vodivost v praxi

Zdroj

Zdroj

Zdroj

Zdroj
Stěny starého domu mají tloušťku 0,5 m, plochu 108 m2 a jsou postaveny z cihel (\(\lambda = 0,6\ \mathrm{W}\cdot\mathrm{m}^{-1}\cdot\mathrm{K}^{-1}\)).
Vypočítejte, kolik tepla projde zdmi za 24 hodin při venkovní teplotě −5 °C a vnitřní teplotě 25 °C.
V tomto příkladu stačí jen dosadit do vzorce hodnoty ve správných jednotkách:
\[ Q = \frac{\lambda St\cdot \Delta T}{d} = \frac{0{,}6\cdot108\cdot(24\cdot3600)\cdot30}{0{,}5}\ \mathrm{J} = 340\ \mathrm{MJ} \]To odpovídá výkonu topení \(P=Q/t=3{,}9\ \mathrm{kW}\).
Proudění
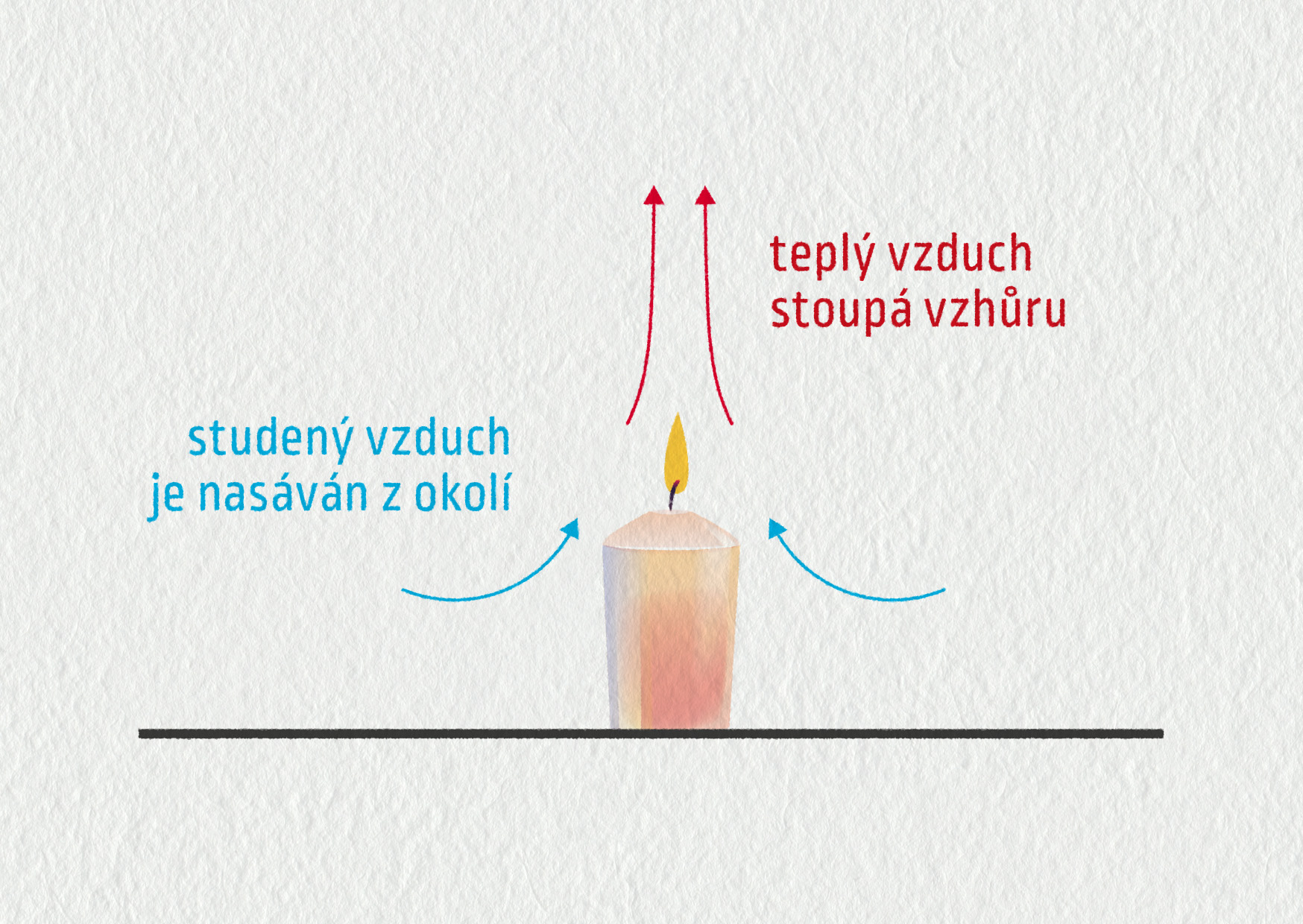
Proudění je převažující způsob přenosu tepla u kapalin a plynů. Proudění může vnikat uměle, například pomocí čerpadla, které pohání vodu v trubkách ústředního topení. V přírodě se často setkáváme s tím, že proudění vzniká samovolně. Dobře si to můžete představit na příkladu hořící svíčky (viz obrázek). Podobně vznikají také vzdušné a mořské proudy, které transportují teplo od rovníku směrem k pólům a rozhodují do velké míry o tom, jaké bude počasí.
Zdroj
Golfský proud transportuje řádově 108 m3 vody za sekundu. U mysu Hatteras v USA, kde se proud odděluje od Amerického pobřeží, je teplotní rozdíl oproti okolní vodě asi 3° C. Určete řádově, kolik tepla transportuje Golfský proud za jeden den.

Zdroj
Začneme výpočtem hmotnosti transportované vody za den (1 den = 86 400 s):
\[ m = 10^8\ \mathrm{m}^3 \cdot 1000\ \mathrm{kg/m}^3 \cdot 86\,400\ \mathrm{s} = 8{,}6\cdot10^{15}\ \mathrm{kg} \]Dále uvažme, že vodu v proudu bylo potřeba ohřát o 3° C vůči okolní vodě. Celkové teplo přepravené za jeden den je pak \(Q=mc\cdot\Delta t=10^{20}\ \mathrm{J}\). Pro představu: to odpovídá celosvětové roční produkci elektrické energie.
Proudění

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj
Záření
Záření nebo také sálání je jev, kterého si všimneme především u velmi horkých těles, jako jsou Slunce či rozpálená kamna. Intenzita vyzařování totiž velmi silně roste s teplotou tělesa. Záření vzniká jako důsledek chaotického pohybu atomů a molekul, proto se mu někdy říká tepelné záření. Přesněji řečeno jde o elektromagnetické záření (podrobněji se o něm dočtete ve 26. kapitole). Na tomto místě si vystačíme s poznatkem, že těleso se může pomocí záření zahřívat (na povrch Země během dne dopadá Sluneční záření), anebo ochlazovat (povrch Země během noci vyzařuje do vesmíru). Bude-li těleso v prostředí o stejné teplotě, jako je teplota tělesa, bude přijaté a vyzářené teplo stejné. V praxi musíme dávat pozor na to, že kovové povrchy mohou tepelné záření částečně odrážet, například hliníková fólie dobře odráží tepelné záření, proto se používá jako tepelná ochrana (viz obrázek). Naopak obyčejné sklo je pro tepelné záření neprůhledné.

Zdroj

