Co se děje s látkou při změně skupenství?

Zdroj
Přemýšleli jste někdy nad tím, proč se mají těstoviny připravovat ve vroucí vodě po určitou dobu? Jaký je zde fyzikální význam varu? Je to prosté: samotný var je z hlediska přípravy potravin zcela nepodstatný. Var nám v hrnci pouze zajišťuje stálou teplotu, která určuje dobu přípravy. Voda začne vařit při necelých 100 °C, a přestože je dál ohřívána na sporáku, tak její teplota již neroste. Veškeré dodávané teplo se spotřebuje na změnu skupenství – tedy uvolnění molekul vody z jejich vazeb. Je třeba dodat, že teplota varu závisí na tlaku vzduchu, který klesá s nadmořskou výškou, jak vidíme v tabulce. Ve větších nadmořských výškách je proto potřeba dobu přípravy patřičně prodloužit.
| Nadmořská výška v m | Tlak v kPa | Teplota varu ve °C |
|---|---|---|
| 0 | 100 | 99,6 |
| 100 | 98,8 | 99,3 |
| 200 | 97,6 | 98,9 |
| 500 | 94,2 | 98,0 |
| 1 000 | 88,6 | 96,4 |
| 2 000 | 78,4 | 93,6 |
| 3 000 | 69,1 | 90,9 |
| 4 000 | 60,8 | 88,6 |
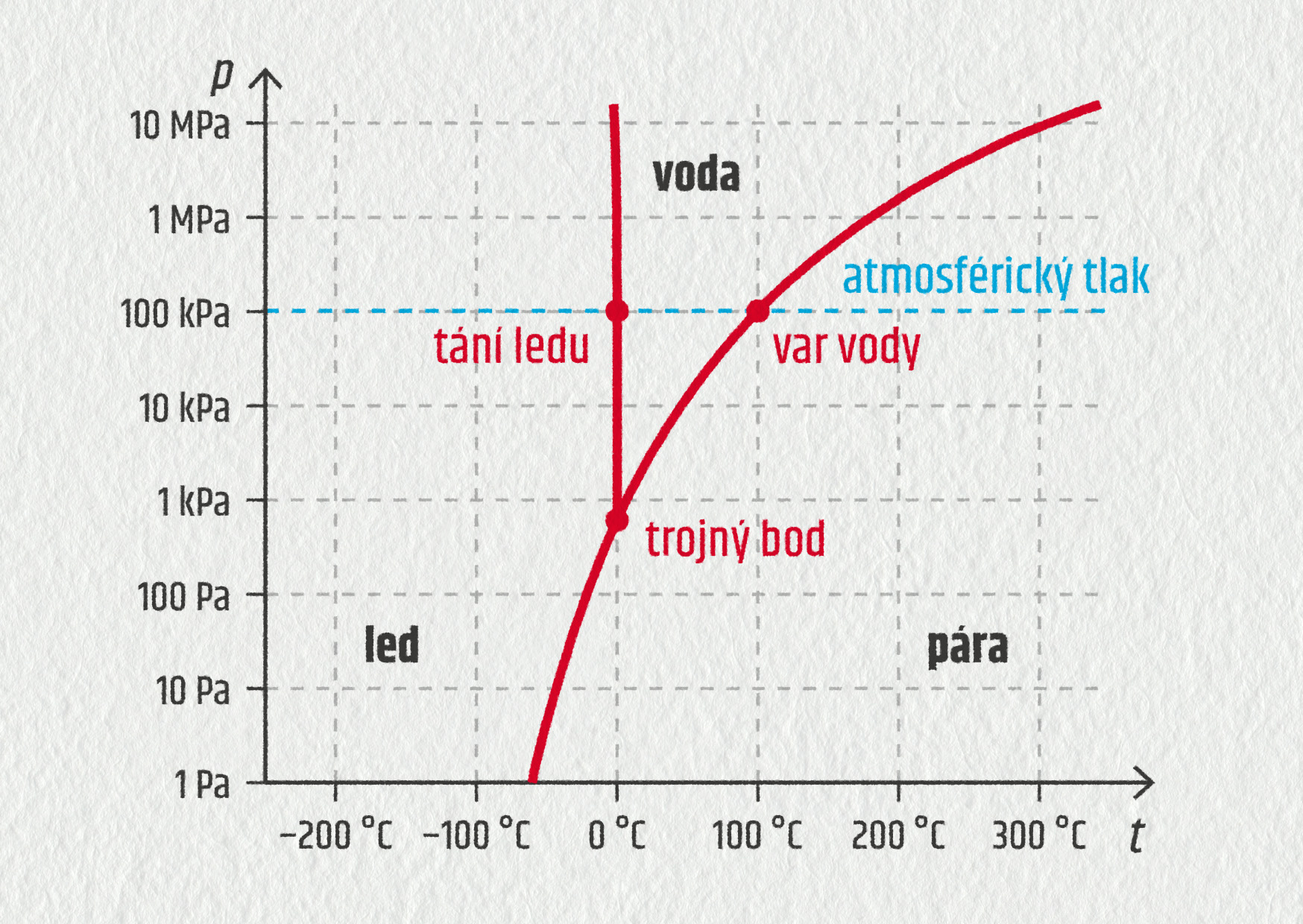
Prozkoumejme nyní podrobněji, co se při změnách skupenství s látkami děje. Pro krystalické látky je typická přesně definovaná teplota tání a teplota varu. Jak jsme ale viděli na příkladu vody, mohou tyto teploty záviset také na tlaku. Z toho vyplývá, že skupenství určité látky je dáno teplotou a tlakem. Chování dané látky za všech možných tlaků a teplot pak můžeme shrnout do grafu; nazývá se fázový diagram.
Zdroj
V diagramu vidíme, že voda za atmosférického tlaku se může vyskytovat v kapalném skupenství v rozumném rozsahu teplot. Snižováním tlaku se prostor pro kapalnou vodu postupně zužuje. Až při tlaku 612 Pa dojde ke splynutí teploty tání a varu. Tento bod, určený teplotou a tlakem, kdy se látka vyskytuje v rovnovážném stavu ve všech třech skupenstvích, nazýváme trojný bod.
Se změnami skupenství je to ještě trochu složitější, než jsme uvedli výše. Kapalná látka se může vypařovat i při nižších teplotách, než je teplota varu. Voda z jezer a moří se vypařuje, prádlo schne a také sníh a led může v atmosféře sublimovat (přecházet z pevného přímo do plynného skupenství). K vysvětlení těchto jevů nám opět poslouží atomová hypotéza. Zatímco při varu dochází k „hromadnému“ přerušování vazeb mezi molekulami v celém objemu kapaliny, při vypařování nastává uvolňování vazeb jen na povrchu kapaliny. S rostoucí teplotou látky se zvyšuje pravděpodobnost, že náhodnými srážkami získají některé molekuly dostatečnou energii k přerušení vazeb. Změny skupenství vody v atmosféře jsou podstatné v meteorologii, proto se o nich můžete dočíst více v kapitole 11.
Změny skupenství

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj
Zdroj

Zdroj

Zdroj
Změny vnitřní energie při změnách skupenství
Při tání nebo vypařování je třeba přerušit vazby mezi atomy (molekulami). Při opačných dějích (tuhnutí a kondenzaci) se naopak vazby vytvářejí. Fyzikálně to můžeme popsat tak, že při změně skupenství dochází ke změně vnitřní potenciální energie. To znamená, že například při tání dodáváme látce teplo, aniž se zvětšuje vnitřní kinetická energie, a tedy i její teplota. Naopak při tuhnutí látka teplo odevzdává, aniž se přitom ochlazuje. Změnu vnitřní potenciální energie spojenou se změnou skupenství dané látky nazýváme zkráceně skupenské teplo \(L\). Podobně jako teplo závisí skupenské teplo na množství látky. Proto se jako charakteristika dané látky používá měrné skupenské teplo \(l\). Platí:
Skupenské teplo
\(L=ml\)
\(m\) = hmotnost
\(l\) = měrné skupenské teplo (vlastnost látky)
Dobrou představu o změnách energie při změnách skupenství nám poskytne naše oblíbená voda.
| tání a tuhnutí | var (vypařování) a kondenzace | |
| měrné skupenské teplo \(l\) | 334 kJ ⋅ kg−1 | 2 260 kJ ⋅ kg−1 |
Porovnejte skupenské teplo vody z tabulky s teplem potřebným k ohřátí 1 kg vody o 100 °C.
\(Q= mc\cdot\Delta t = 1\cdot4180\cdot100\ \mathrm{J} = 418\ \mathrm{kJ}\).
Teplo potřebné k vypaření vody je skoro pětkrát větší než teplo potřebné k jejímu ohřátí z 0 °C na 100 °C!
Hodnoty měrného skupenského tepla pro konkrétní látky je možné vyhledat nebo změřit (můžete si to vyzkoušet v praktickém cvičení). Skupenské teplo hraje důležitou roli v mnoha přírodních procesech. Více se o tom dozvíte v galerii a příkladech.

Zdroj
V extrémních podmínkách, například v poušti při nízké vlhkosti vzduchu, může člověk vypotit kolem jednoho litru vody za hodinu. Určete výkon takového ochlazování.

Zdroj
Výkon ochlazování určíme jako podíl odebrané energie a času: \(P=L/t=ml/t=630\ \mathrm{W}\).
Poznámka: Měrné skupenské teplo vypařování závisí na teplotě, při které k němu dochází. Je vždy o něco větší než odpovídající skupenské teplo varu. Rozdíl je však poměrně malý (do 10 %) a v tomto příkladu nehraje velkou roli.
První elektrické ledničky dorazily do našich domácností teprve ve dvacátých letech 20. století. Předtím se potraviny chladily pomocí ledu.
- Popište a vysvětlete, jak efektivně realizovat takové chlazení potravin pomocí ledu.
- Vypočítejte, kolik tepla dokáže odebrat ze svého okolí 1 m3 ledu, aniž se změní jeho teplota.
a) V zimě nasbíráme v přírodě velké kusy ledu. Ty umístíme do dobře tepelně izolované místnosti. Led bude postupně tát a přitom odebírat teplo z okolí, aniž se zvětší jeho teplota, která bude stále 0 °C.
b) \(L=ml=\varrho Vl = 917\ \mathrm{kg/m}^3\cdot 1\ \mathrm{m}^3 \cdot 334\,000\ \mathrm{J/kg/K} = 306\ \mathrm{MJ}\).
Na závěr jsme si nechali nejtěžší typ úlohy. Podobně jako u tepelné výměny, musí i při změnách skupenství platit, že celková energetická bilance v izolované soustavě je nulová.
V kelímku jsou 3 dl vody o teplotě 15 °C. Do nádoby hodíme kostku ledu o hmotnosti 50 g a teplotě −5 °C. Určete výslednou teplotu vody v kelímku. Tepelnou kapacitu kelímku a ztráty tepla do okolí neuvažujte.
V příkladu postupujeme obdobně jako při výpočtu tepelné výměny. Kromě tepla však musíme uvažovat ještě skupenské teplo. Další neznámou je výsledný stav soustavy. V principu jsou dvě možnosti:
- Všechen led roztaje a z něj vzniklá voda se bude ohřívat. Výsledná teplota bude nad nulou.
- Teplo odevzdané vodou nebude stačit na roztátí veškerého ledu. Výsledná teplota bude 0 °C a určitá část ledu zůstane v pevném skupenství.
O tom, která varianta nastane, rozhodneme porovnáním tepla, které může odevzdat voda, a tepla, které může přijmout led.
Voda se ochlazuje na 0 °C: \(Q_\mathrm{V} = m_\mathrm{V}c_\mathrm{V}\Delta t_\mathrm{V} = 0{,}3\ \mathrm{kg}\cdot 4180\ \mathrm{J/kg/K}\cdot (15-0)\ \mathrm{K}= 18\,810\ \mathrm{J}\).
Led se ohřívá na 0 °C: \(Q_\mathrm{L} = m_\mathrm{L}c_\mathrm{L}\Delta t_\mathrm{L} = 0{,}05 \cdot 2050 \cdot (0-(-5))\ \mathrm{J} = 512\ \mathrm{J}\).
Led taje: \(L = m_\mathrm{L}l = 0{,}05\ \mathrm{kg}\cdot 334\,000\ \mathrm{J/kg} = 16\,700\ \mathrm{J}\).
Máme \(Q_\mathrm{V} > Q_\mathrm{L} + L\). To znamená, že všechen led roztaje. Můžeme zapsat celkovou tepelnou bilanci už s neznámou výslednou teplotou \(t\) (teplotu tání 0 °C označíme jako \(t_0\)):
\[ m_\mathrm{V}c_\mathrm{V}(t_\mathrm{V} - t) = m_\mathrm{L}c_\mathrm{L}(t_0 - t_\mathrm{L}) + m_\mathrm{L}l + m_\mathrm{L}c_\mathrm{V}(t - t_0) \](Všimněte si posledního členu – voda vzniklá z ledu se ohřívá z 0 °C na \(t\).)
Vzhledem k velkému množství veličin volíme v tomto případě dosazení čísel do rovnice. Po dosazení a úpravě nám vyjde \(t=1\ ^\circ\mathrm{C}\).

