Jak definujeme teplotu?
Kde se setkáváme s měřením teploty
Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj
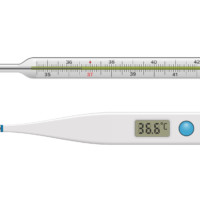
Jak dokumentuje úvodní galerie, s teplotou a jejím měřením se setkáváme na každém kroku. Teplota je také jednou ze sedmi základních veličin soustavy SI. Možná vás ale překvapí, že první teplotní stupnice a první pořádné teploměry byly vynalezeny až na začátku 18. století. Definovat a správně měřit teplotu totiž není tak jednoduché, jak by se mohlo na první pohled zdát. Proč tomu tak je? Jak jsme naznačili v úvodu této kapitoly, teplota je spojena s kinetickou energií částic, tedy s jejich neustálým chaotickým pohybem. Ten se ale nedá přímo měřit, proto je nutné měřit teplotu nepřímo – pomocí nějaké jiné fyzikální veličiny, která je na teplotě závislá. Tou může být objem plynu či kapaliny nebo třeba elektrický odpor polovodiče (známe z deváté kapitoly). Vnímat teplotu dokážeme i my lidé, ale nepříliš spolehlivě. Můžete se o tom přesvědčit jednoduchým pokusem, jehož princip najdete v popisu obrázku.

Zdroj
K tématu praktické konstrukce teploměrů a teplotních stupnic se ještě vrátíme. Měření teploty je založeno na existenci rovnovážného stavu. Vysvětlíme si to na jednoduchém příkladu (viz obrázek): mějme dvě tělesa, která jsou ve vzájemném kontaktu, ale jinak od okolí izolována. Je-li na začátku jedno těleso teplejší než druhé, musí jeho částice při nárazech předávat část své energie pomalejším částicím chladnějšího tělesa. Takto se postupně energie, a tedy i teploty těles vyrovnají. Odborně řečeno: soustava dospěje do rovnovážného stavu.
Zdroj
Proč je to tak důležité? Teploměr nám vždy ukazuje svoji vlastní teplotu. Teprve za předpokladu, že byl v rovnovážném stavu s měřeným tělesem, můžeme říct, že teplota měřeného tělesa je stejná jako teplota teploměru. Všichni to dobře známe při měření lékařským teploměrem; přiložíme teploměr a čekáme, až nastane rovnováha (teplota se přestane měnit). Teprve pak přečteme teplotu na teploměru.
Nyní můžeme definovat teplotní stupnici. V dnešní době se ve světě používají tři: Celsiova, Fahrenheitova a termodynamická. Každá stupnice je definována pomocí dvou bodů.
V případě Celsiovy stupnice je to bod tání ledu (0 °C) a bod varu vody za normálního tlaku (100 °C). Právě díky přehlednému navázání na změny skupenství vody (mráz = záporná teplota) používáme tuto stupnici dodnes. Pro teplotu ve °C je zvykem používat symbol \(t\).
Původní Fahrenheitova stupnice vycházela z těchto bodů: nejnižší teplota, jaké se podařilo Fahrenheitovi dosáhnout smícháním chloridu amonného, vody a ledu (0 °F) a normální tělesná teplota člověka (96 °F). Později byly referenční body upraveny na 32 °F pro bod mrazu vody a 212 °F pro bod varu vody. Dnes je používaná především v USA.
Nejnovější termodynamická stupnice je zhruba o jedno století mladší. Zavedl ji skotský fyzik William Thomson (lord Kelvin) a podle něj má svůj název jednotka kelvin – základní jednotka teploty v soustavě SI. V té době už fyzikové věděli, že existuje nejnižší možná teplota, při které by se úplně zastavil chaotický pohyb atomů. Tato teplota se nazývá absolutní nula (0 K). K definici stupnice pak stačí jediný bod – trojný bod vody (273,16 K). Trojný bod představuje rovnovážný stav všech tří skupenství vody (viz kapitola 11) a v Celsiově stupnici odpovídá teplotě 0,01 °C. Díky tomu, že termodynamická teplota nemůže být záporná, usnadňuje nám zápis mnoha fyzikálních zákonů (s některými se setkáme i v naší učebnici). Pro odlišení se pro ni používá písmeno \(T\). Srovnání všech tří stupnic ukazuje následující obrázek:

Zdroj
V obrázku si můžete všimnout, že převod mezi termodynamickou a Celsiovou stupnicí je snadný, protože stupnice mají stejně velké dílky a liší se pouze posunem o 273,15. Pro teplotní rozdíly proto platí \(\Delta T = \Delta t\).
Termodynamická teplota: značka \(T\), jednotka K (kelvin), převod: \(T = (\{t\}+273{,}15)\ \mathrm{K}\)
Spodní hranicí teploty je absolutní nula (0 K). Teploty jen o několik setin kelvinu vyšší než absolutní nula už dokážeme vytvořit v laboratoři. Při nízkých teplotách se objevuje velmi zvláštní chování hmoty – například supravodivost (viz poznámka v kapitole 8) nebo supratekutost. Horní hranice teploty nemá teoretický limit. Například v jádrech hvězd dosahují teploty milionů kelvinů. Takto vysoké teploty umožňují slučování jader, které dodává hvězdám energii (viz jaderná fúze – kapitola 27).
| Situace | Teplota ve °C | Teplota v K |
|---|---|---|
| absolutní nula | −273,15 | 0 |
| teplota varu helia | –269 | 4 |
| teplota varu dusíku | −196 | 77 |
| nejnižší teplota naměřená na Zemi | −89 | 184 |
| teplota tání ledu | 0 | 273 |
| teplota varu vody (za normálního tlaku) | 100 | 373 |
| teplota tání železa | 1 538 | 1 811 |
| teplota povrchu Slunce (přibližně) | 5 500 | 5 800 |
| teplota v jádru Slunce (přibližně) | 15 ⋅ 106 | 15 ⋅ 106 |
Teplota tání rtuti je –39 °C. Kolik je to kelvinů? [...] K (zaokrouhlete na celé číslo)
Jak měříme teplotu?
Teplotu musíme měřit nepřímo, pomocí jiné fyzikální veličiny, která je na teplotě závislá. Z toho vychází také různé druhy teploměrů.
Kapalinový teploměr
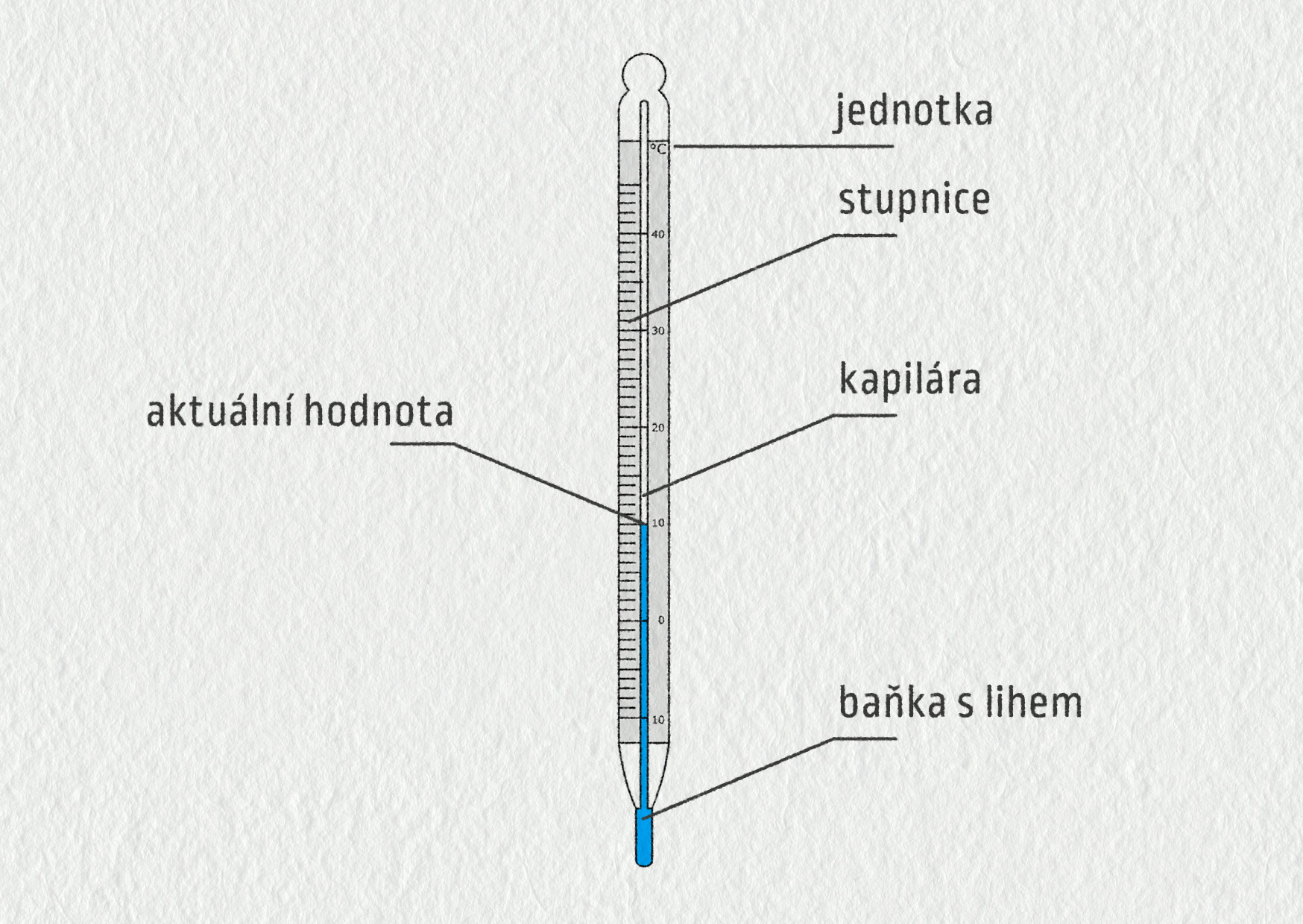
Kapalinový teploměr měří teplotu pomocí rozpínání kapaliny. Jelikož je roztažnost kapalin velmi malá, musí být k baňce s kapalinou připojena tenká trubička – kapilára (viz obrázek).
Zdroj
Rozpínání kapalin je přibližně lineární, proto mohou být dílky na stupnici teploměru stejně dlouhé. Řečeno matematicky – změna objemu \(\Delta V\) je přímo úměrná změně teploty \(\Delta t\).
\( \Delta V = V_0 \cdot \beta \cdot \Delta t\), \(\beta\) = koeficient teplotní objemové roztažnosti, \(V_0\) = původní objem kapaliny
V kapalinových teploměrech se nejčastěji používá obarvený líh, jeho koeficient teplotní objemové roztažnosti je \(\beta=1{,}12\cdot10^{-3}\ \mathrm{K}^{-1}\). To znamená, že při ohřátí o 1 K (1 °C) bude platit \(\Delta V = 0{,}00112 V_0\) , tedy objem lihu se při ohřátí o 1°C zvětší přibližně o jednu tisícinu původní hodnoty. Důležitý je u každého teploměru také jeho rozsah. Lihový teploměr může teoreticky fungovat maximálně v rozmezí od −114 °C (teplota tuhnutí) do 78 °C (teplota varu).
Lihový teploměr je tvořen baňkou o objemu 1 ml a kapilárou o vnitřním průměru 0,6 mm. Jakou délku bude mít dílek na stupnici teploměru, který odpovídá změně teploty o 1 °C?
Nejdříve vypočítáme, o kolik naroste objem lihu při \(\Delta t = 1\ ^\circ\mathrm{C}\). Budeme počítat v cm3, neboť 1 ml = 1 cm3.
\[ \Delta V = V_0 \cdot \beta \cdot \Delta t = 1 \cdot 1,12 \cdot 10^{-3} \cdot 1\ \mathrm{cm}^3 = 0{,}001\ \mathrm{cm}^3 \]Kapilára má tvar válce o průměru \(d\), a její objem tedy můžeme vyjádřit jako \(V=Sh=\pi d^2/4\cdot h\). Pokud nyní za \(V\) dosadíme vypočítané zvětšení objemu lihu \(\Delta V\), dostaneme hledanou výšku \(h\) odpovídající jednomu dílku na stupnici (dosazujeme hodnoty v cm a cm3):
\[ h= \frac{4V}{\pi d^2} = \frac{4\cdot0{,}001}{3{,}14\cdot0{,}06^2}\ \mathrm{cm} = 0{,}35\ \mathrm{cm}\]Plynový teploměr
Plynový teploměr je založen na principu rozpínání plynu v závislosti na teplotě. Byl to historicky první druh teploměru, neboť má jednoduchou konstrukci.

Zdroj
Takto vyrobený plynový teploměr je ovšem prakticky těžko použitelný, protože plyn v nádobě se bude rozpínat také v závislosti na tlaku okolního vzduchu. Profesionální plynový teploměr je proto hermeticky uzavřený.
Bimetalový teploměr
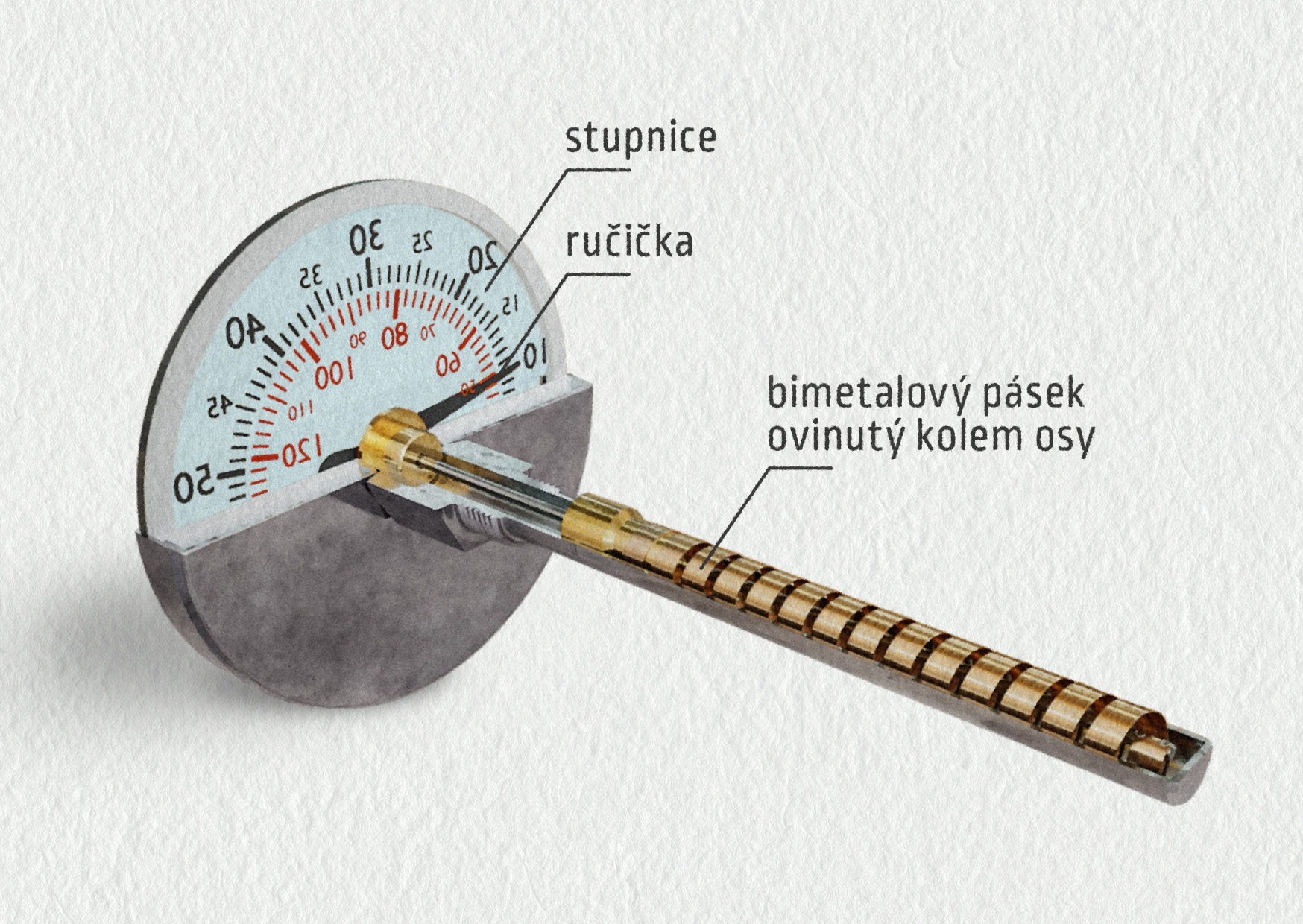
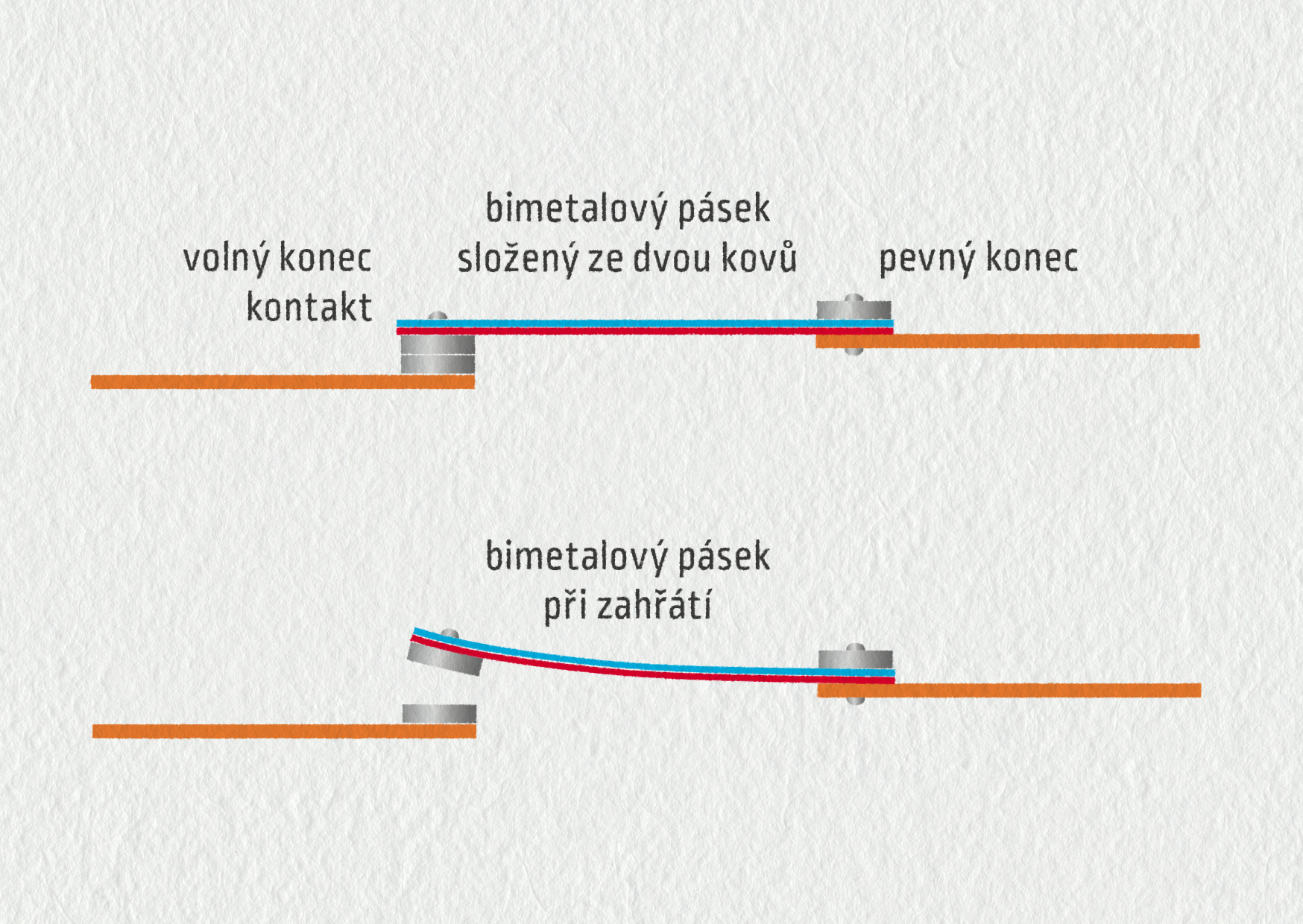
Bimetalový teploměr využívá teplotní roztažnosti kovů. Bimetal je pásek ze dvou kovů o různých tepelných roztažnostech (například ocel a bronz), které jsou navzájem pevně spojeny (slisovány nebo svařeny). Při zahřátí se jeden z dvojice kovů roztahuje víc než druhý, a tím dochází k ohýbání pásku. Někdy je pásek stočený do tvaru šroubovice, čímž dosáhneme větší citlivosti (viz obrázek). Bimetal se kromě teploměru využívá také v mechanickém termostatu (viz obrázek), který zajišťuje stálou teplotu v troubě, žehličce a podobných tepelných spotřebičích.
Zdroj
Zdroj
Teplotní roztažnost pevných látek je sama o sobě důležitým jevem. Podobně jako u kapalin můžeme změnu délky s teplotou modelovat přibližně jako lineární. Také vzorec je velmi podobný – změna délky \(\Delta l\) je přímo úměrná změně teploty \(\Delta t\).
\(\Delta l = l_0 \cdot \alpha \cdot \Delta t\), \(\alpha\) = koeficient teplotní délkové roztažnosti, \(l_0\) = původní délka.
Koeficient teplotní délkové roztažnosti například pro ocel je \(\alpha = 1{,}2\cdot10^{-5}\ \mathrm{K}^{-1}\). To znamená, že při ohřátí o 1 K (1 °C) bude platit \(\Delta l = 0{,}000012l_0\), tedy délka ocelového předmětu se při ohřátí o 1 °C zvětší o 12 miliontin původní hodnoty.
Ocelové lano o délce 50 m se ohřálo o 20 °C. Jak se změnila jeho délka?
\(\Delta l = l_0 \cdot \alpha \cdot \Delta t = 50 \cdot 0{,}000 012 \cdot 20\ \mathrm{m}= 0,012\ \mathrm{m} = 12\ \mathrm{mm}\).
To není mnoho, ale v mnoha konstrukcích je třeba i s takto nenápadným jevem počítat.
Některé příklady, kde se s délkovou roztažností setkáme v praxi, najdete v galerii.
Teplotní roztažnost

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj
Odporový teploměr
Odpor vodičů i polovodičů závisí na teplotě. U polovodičů je tato závislost mnohem výraznější, proto se používají pro měření teploty speciální polovodičové prvky – termistory. Princip a zapojení termistoru jsou podrobně vyloženy v 9. kapitole. Z této kapitoly také víme, že velkou výhodou termistoru je snadný převod teploty na napětí. Používá se proto převážně tam, kde je informace o teplotě dále digitálně zpracovávána. Termistory jsou omezeny teplotním rozsahem cca −50 °C až 150 °C. Pro větší teplotní rozsahy a přesnější měření se používají teploměry využívající platinu nebo nikl.
Teplotu je možné měřit také pomocí termočlánku – viz poznámka termoelektrický jev v osmé kapitole.
Radiační teploměr
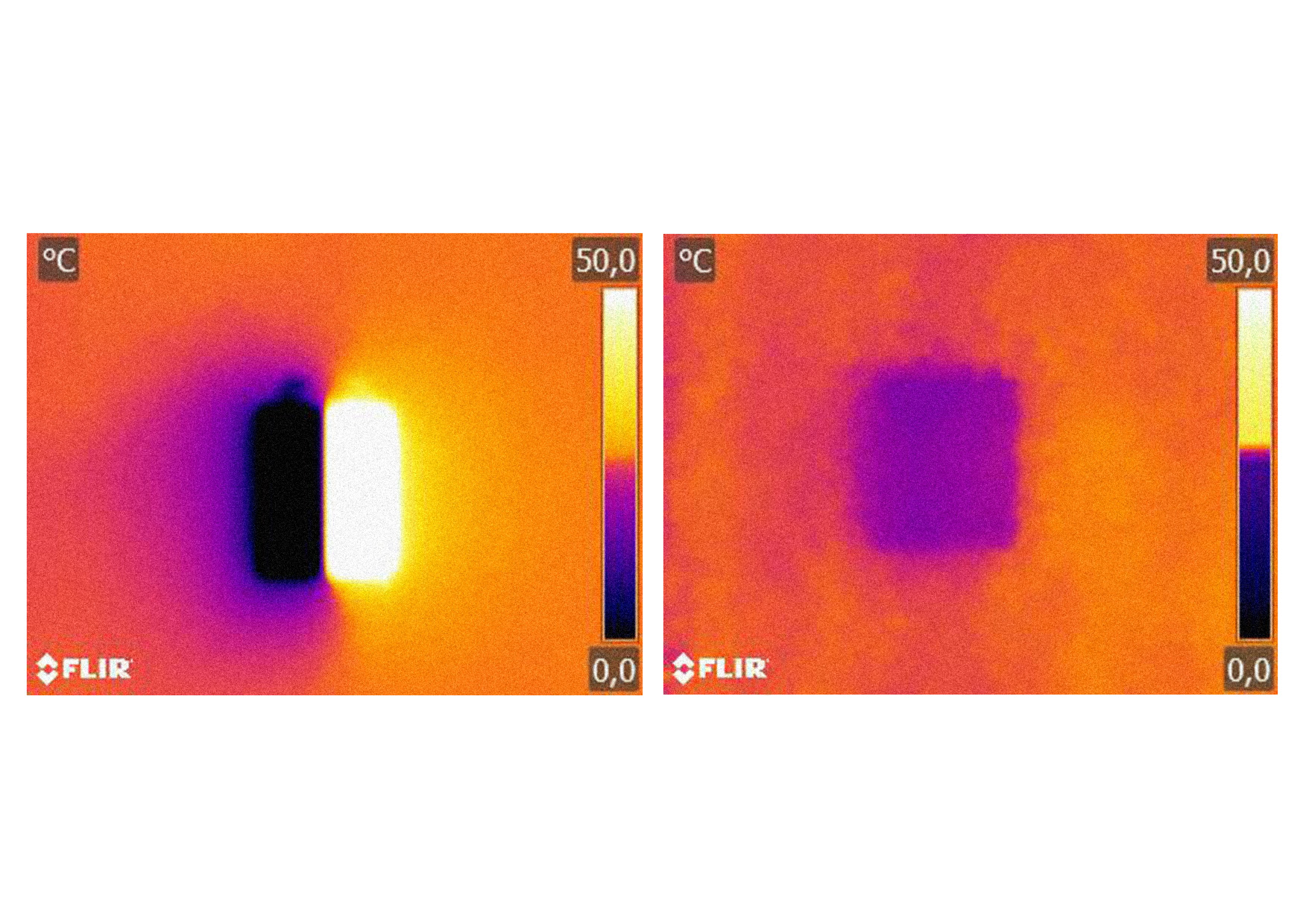
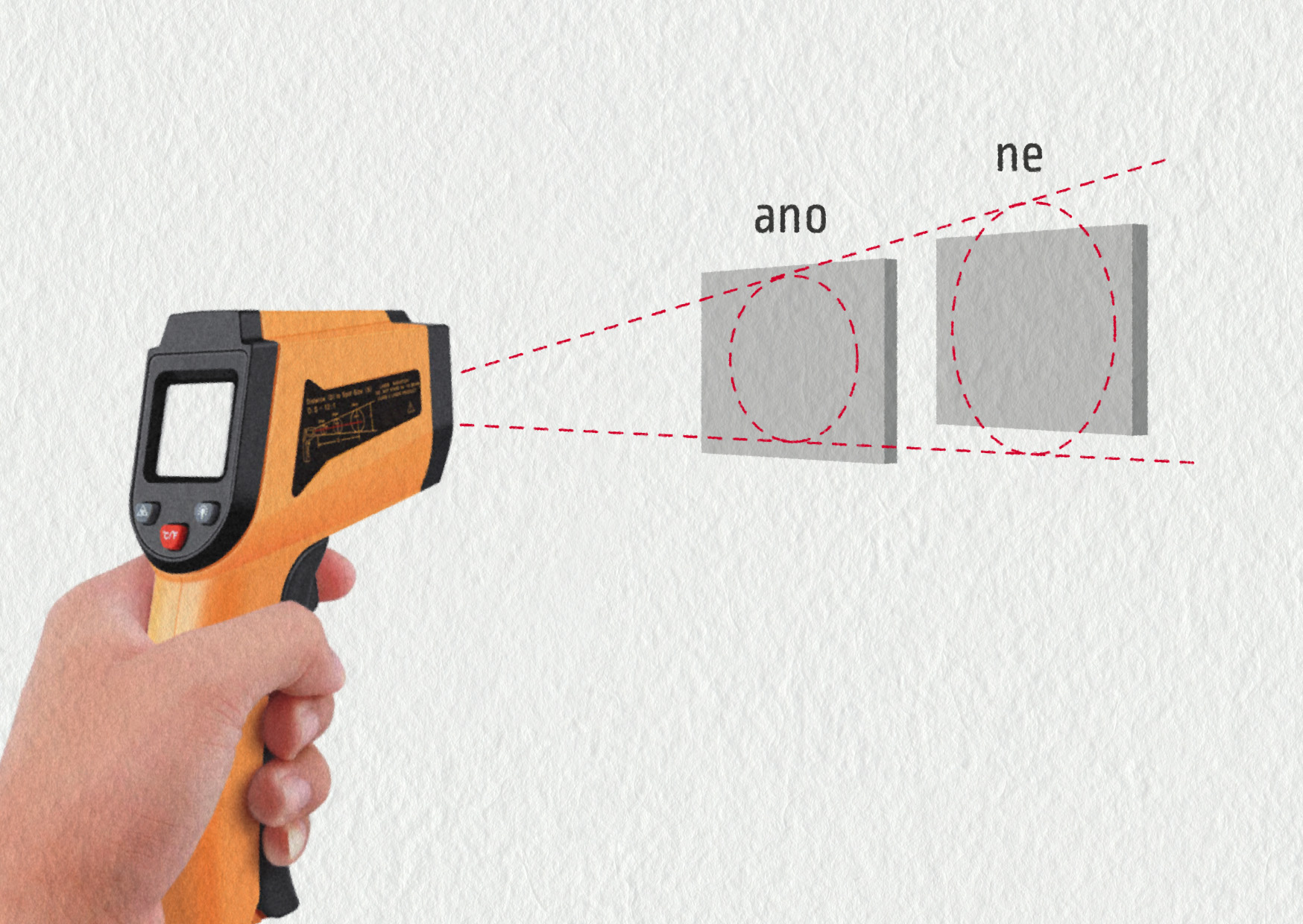
Radiační teploměr umožňuje bezkontaktní měření teploty. Měření teploty na dálku je možné díky tomu, že každé těleso vyzařuje elektromagnetické záření. V případě těles o teplotách do cca 500 °C se jedná pouze o infračervené záření, které je okem neviditelné (podrobněji v kapitole 26). Detektor v teploměru dokáže zaznamenat jeho intenzitu a z ní odvodit teplotu tělesa. V praxi je důležité, že při měření musí měřené těleso pokrývat celý zorný úhel teploměru (viz obrázek).
Zdroj
Na podobném principu funguje také termokamera, která dokáže pořizovat snímky v infračerveném spektru (viz galerie – Kde se setkáváme s měřením teploty).
V následujících příkladech jsou popsány nevhodné způsoby měření teploty. U každého příkladu vysvětlete, proč nebude měření fungovat správně, a navrhněte lepší metodu.
- Jana navrhuje měřit teplotu vody v hrnci při vaření tak, že do hrnce vloží lihový teploměr.
- Olga navrhuje měřit teplotu vzduchu na osluněné pláži tak, že položí lihový teploměr na písek a počká 2 minuty. Poté odečte teplotu z teploměru.
- Tomáš navrhuje měřit teplotu pacienta tak, že na jeho obličej ze vzdálenosti cca 1,5 m namíří radiační teploměr.
- Vojta navrhuje měřit teplotu dešťových kapek tak, že nachytá déšť do skleničky a pak do vzorku ponoří termistorový teploměr.
- David navrhuje měřit teplotu ledové kostky tak, že k ní přiloží lihový teploměr a po 1 minutě odečte teplotu.
- Mirek navrhuje měřit teplotu v troubě tak, že namíří radiační teploměr přes skleněná dvířka do trouby a odečte teplotu.
- Lihový teploměr tak vysokou teplotu nevydrží. Pro tyto účely se používá buď kapalinový teploměr se speciální kapalinou, nebo teploměr termistorový.
- Teploměr bude silně ovlivněn zářením ze Slunce. Navíc písek bude rozpálený. Pro měření teploty vzduchu je potřeba mít teploměr ve stínu a dál od ostatních předmětů.
- Z takové vzdálenosti bude v zorném úhlu teploměru nejen celá hlava, ale i její okolí. Je potřeba měřit teplotu ze vzdálenosti kolem 10 cm.
- Kapky jsou malé a ve skleněné nádobě se rychle ohřejí. Bylo by možné nachytat kapky do nádoby z pěnového polystyrénu, která nebude kapky tolik ohřívat.
- Led bude na vzduchu tát. Popsaným způsobem tak změříme spíš teplotu vody, která se na ledové kostce objeví. Teplotu ledu je potřeba měřit ihned po vytažení z mrazáku, nejlépe rychlým termistorovým nebo radiačním teploměrem.
- Infračervené záření (narozdíl od světla) neprojde přes skleněná dvířka. Je potřeba troubu otevřít.

