Pomocí rychlosti dokážeme popsat, jakým směrem a jak rychle se hmotný bod pohybuje. Rychlost je vektorová veličina, může se měnit její velikost i její směr. Proto definujeme zrychlení jako vektorovou veličinu, která vyjadřuje časové změny rychlosti, tedy změny její velikosti i směru. Opět pouze rozšíříme definici zrychlení ze 3. kapitoly \(a_x=\Delta v_x/\Delta t\) do prostoru.
\(\Delta\Vec{v}\) – změna rychlosti, která proběhla během časového intervalu \(\Delta t\).
Okamžité zrychlení: \(\Delta t\) – velmi malé
Průměrné zrychlení: \(\Delta t\) – celková doba pohybu
Jednotkou zrychlení je m ⋅ s−2 a jeho směr je shodný se změnou rychlosti \(\Delta\Vec{v}\).
Okamžitá rychlost se matematicky přesně definuje pomocí limity, která pracuje s nekonečně malou změnou \(\Delta\Vec{v}\) za nekonečně krátkou dobu \(\Delta t\), takto:
\[ \Vec{v} = \lim_{\Delta t\to0} \frac{\Delta\Vec{r}}{\Delta t} \]Podobně můžeme okamžité zrychlení vyjádřit pomocí limity jako
\[ \Vec{a} = \lim_{\Delta t\to0} \frac{\Delta\Vec{v}}{\Delta t} \]V matematice tato limita vyjadřuje derivaci veličiny podle času. Můžeme tedy psát
\[ \begin{aligned} \Vec{v} &= \lim_{\Delta t\to0} \frac{\Delta\Vec{r}}{\Delta t} = \frac{\mathrm{d}\Vec{r}}{\mathrm{d}t} \\ \Vec{a} &= \lim_{\Delta t\to0} \frac{\Delta\Vec{v}}{\Delta t} = \frac{\mathrm{d}\Vec{v}}{\mathrm{d}t} \\ \end{aligned} \]Protože rychlost je derivací polohového vektoru podle času, vypočítáme, že zrychlení je druhou derivací polohy podle času:
\[ \Vec{a} = \frac{\mathrm{d}\Vec{v}}{\mathrm{d}t} = \frac{\mathrm{d}^2\Vec{r}}{\mathrm{d}t^2}\;. \]Téma si můžete připomenout také ve 3. kapitole. Zde se jednalo o pohyby na přímce.
Podívejme se nyní na konstrukci zrychlení v následujícím řešeném příkladu.
Na následujícím obrázku je znázorněno pět poloh tělesa. Interval, který uplynul mezi označením dvou po sobě jdoucích poloh, je 0,025 s. Zkonstruujte vektor zrychlení v bodě M3.
Doporučené měřítko: vektor rychlosti: \(1\ \mathrm{cm}\sim20\ \mathrm{cm\cdot s}^{-1}\), vektor zrychlení: \(1\ \mathrm{cm}\sim150\ \mathrm{cm\cdot s}^{-2}\).
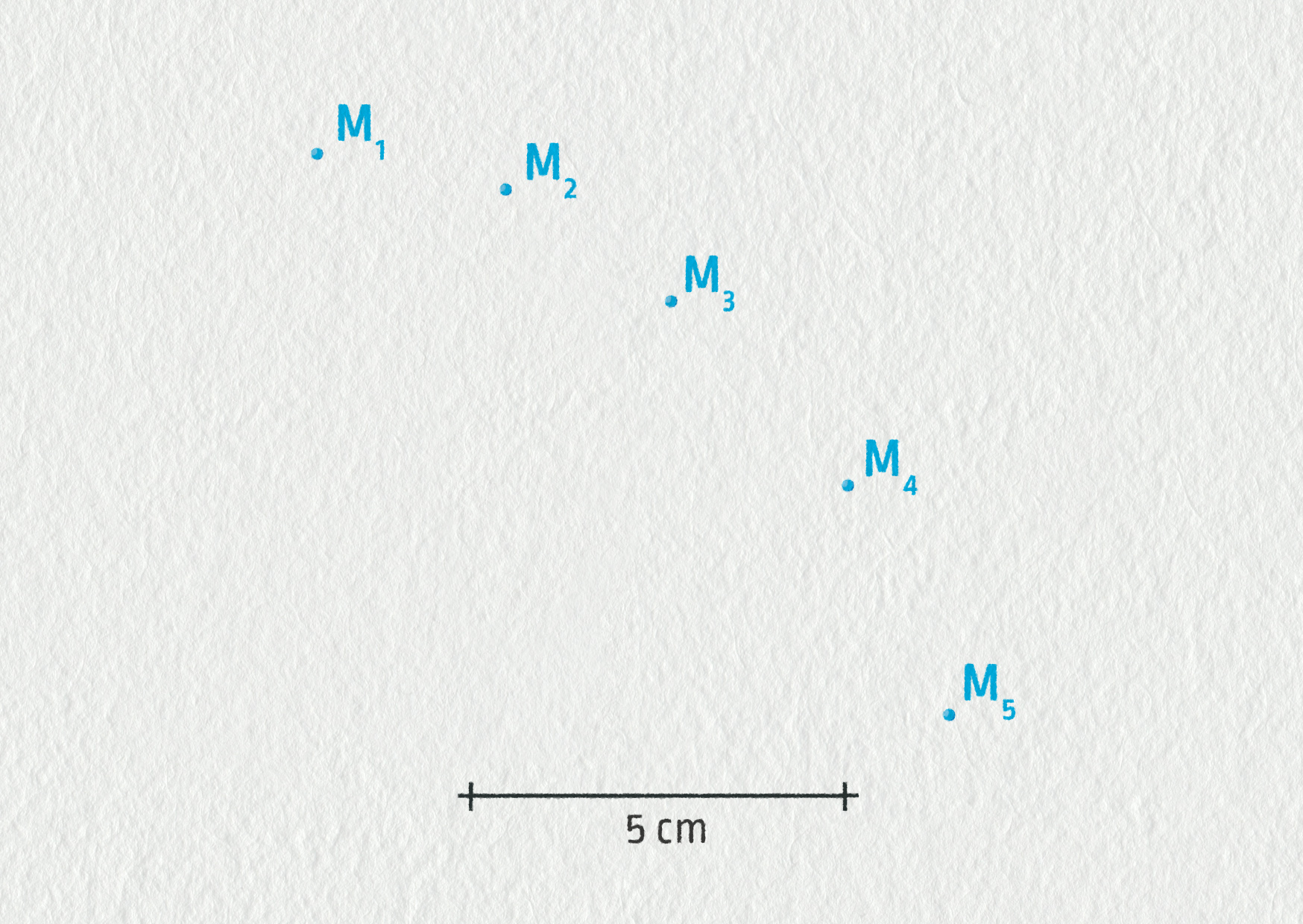
Zdroj
Zkrácený postup konstrukce si můžete prohlédnout na následující animaci https://www.geogebra.org/calculator/b85whfzs.
Pokud budete sami rýsovat, pracovní list je k dispozici zde.
Ke zjištění (okamžitého) zrychlení v bodě M3 budeme pracovat na nejmenším okolí bodu M3, tedy M2 a M4. Vyjděme z definice zrychlení
\[ \Vec{a}_3 = \frac{\Vec{v}_4-\Vec{v}_2}{2\tau}\;. \]Nejprve tedy musíme sestrojit vektory rychlosti v bodech M2 a M4. Postup jsme popsali v předchozím řešeném příkladu. Následně přeneseme vektory \(\Vec{v}_4\) a \(-\Vec{v}_2\) do bodu M3, kde je vektorově sečteme. Změříme velikost vektoru \(|\Delta\Vec{v}|=75\ \mathrm{cm\cdot s}^{-1}\). Velikost vektoru zrychlení má hodnotu
\[ a_3 = \frac{75\ \mathrm{cm\cdot s}^{-1}}{2\cdot0{,}025\ \mathrm{s}} = 1500\ \mathrm{cm\cdot s}^{-2}\;. \]Narýsujeme vektor zrychlení v bodě M3 ve zvoleném měřítku. Tento vektor je rovnoběžný s vektorem \(\Delta\Vec{v}\).
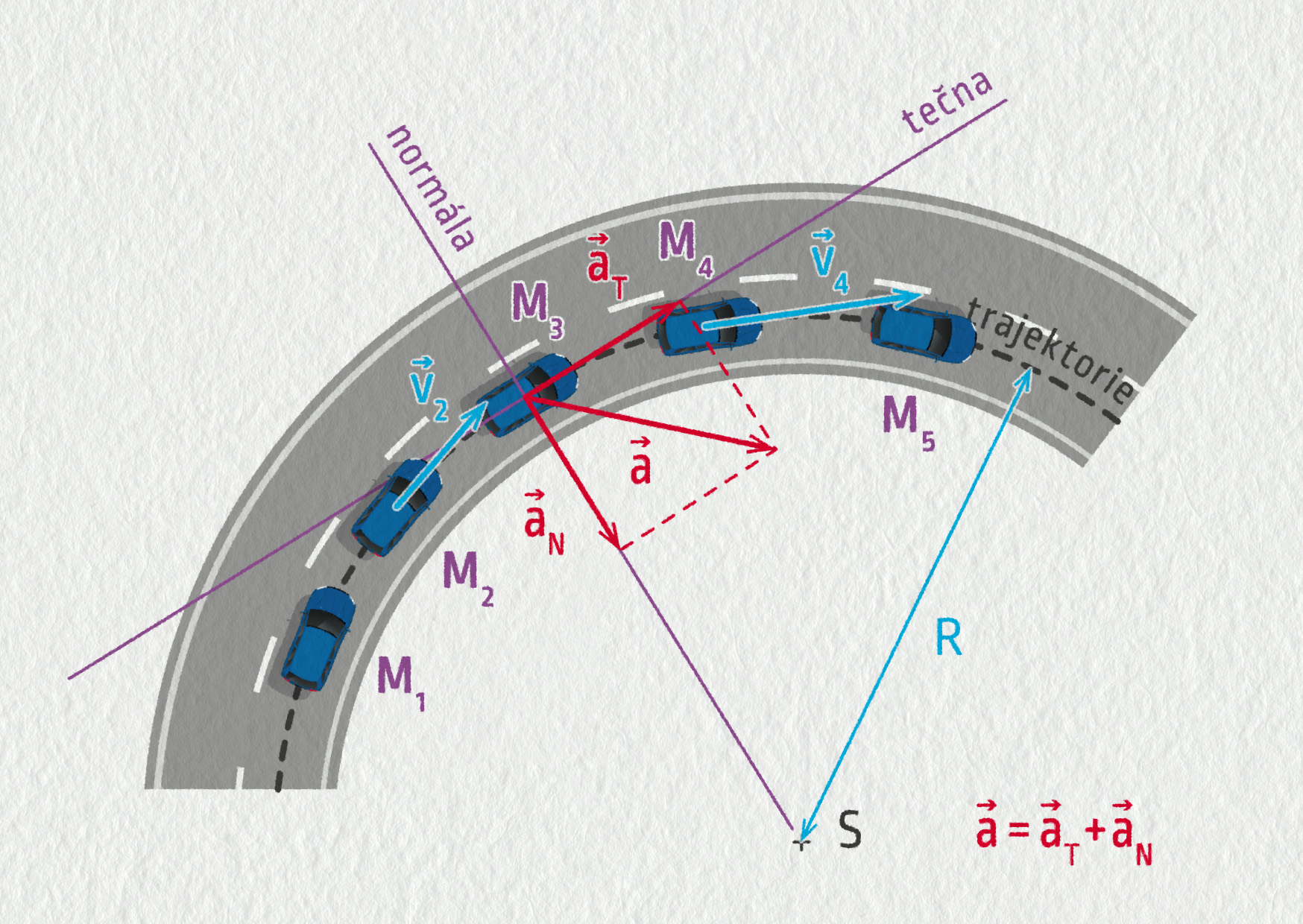
Často je velmi užitečné rozložit zrychlení nikoliv do složek daných souřadnicovými osami \(x\) a \(y\), ale do směru tečny a normály (kolmice k tečně) k trajektorii v daném bodě.
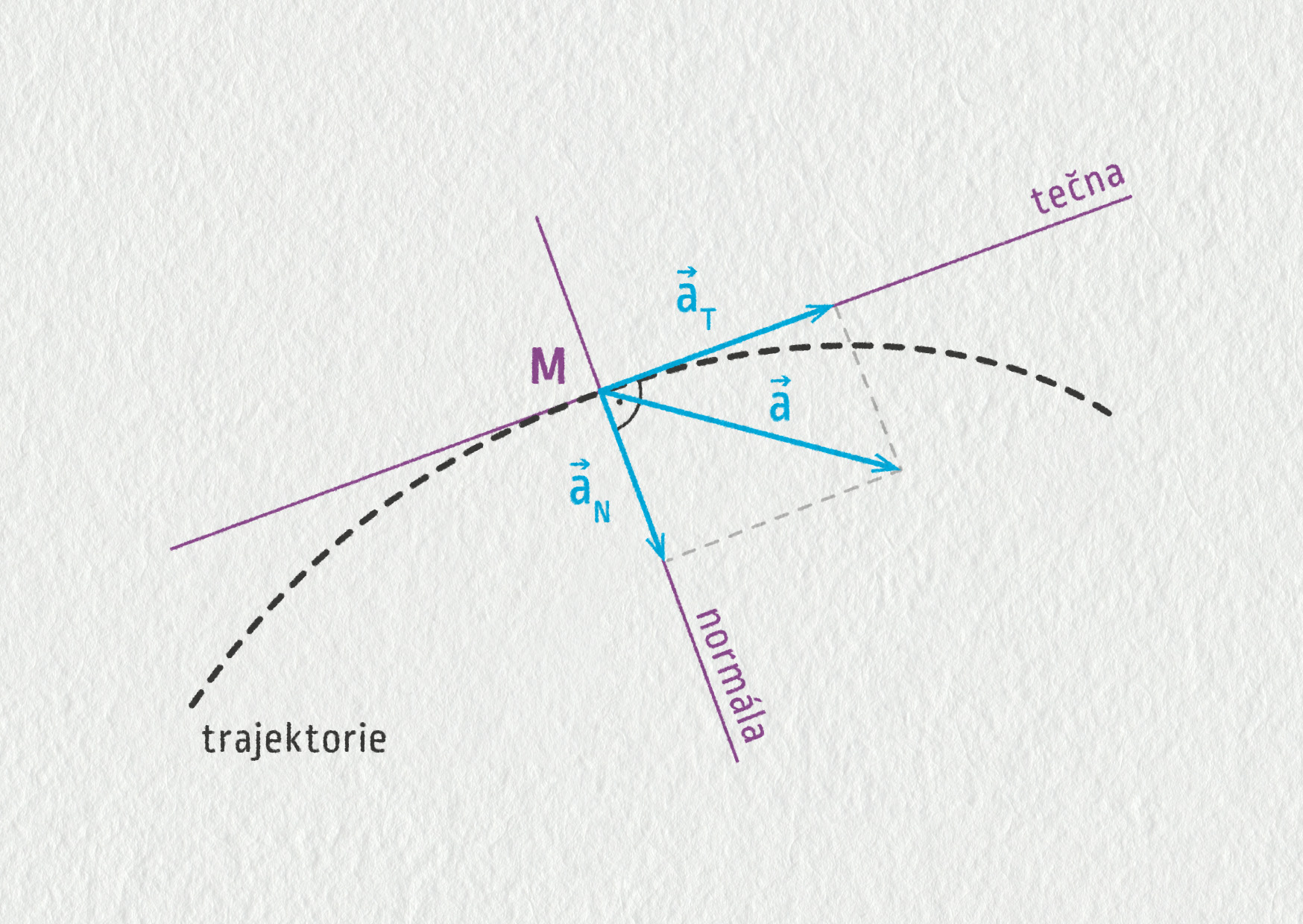
Zdroj
Dostaneme tak tečné zrychlení \(\Vec{a}_\mathrm{T}\) a normálové zrychlení \(\Vec{a}_\mathrm{N}\), přičemž platí \(\Vec{a}=\Vec{a}_\mathrm{T}+\Vec{a}_\mathrm{N}\). Jaký je jejich význam? Rychlost má dvě vlastnosti: velikost a směr. Tečné zrychlení popisuje, jak se mění velikost rychlosti, normálové zrychlení popisuje, jak se mění směr rychlosti.
Ukažme si to na příkladu jedoucího automobilu:
1) Auto zrychluje na přímém úseku silnice. Jeho rychlost nemění směr, pouze velikost, a proto jeho normálové zrychlení musí být nulové. Zrychlení tělesa je jen tečné (\(\Vec{a}=\Vec{a}_\mathrm{T}\)) a určuje, jak se mění velikost rychlosti. Pro velikost tečného zrychlení obecně platí \(a_\mathrm{T}=\Delta v/\Delta t\).
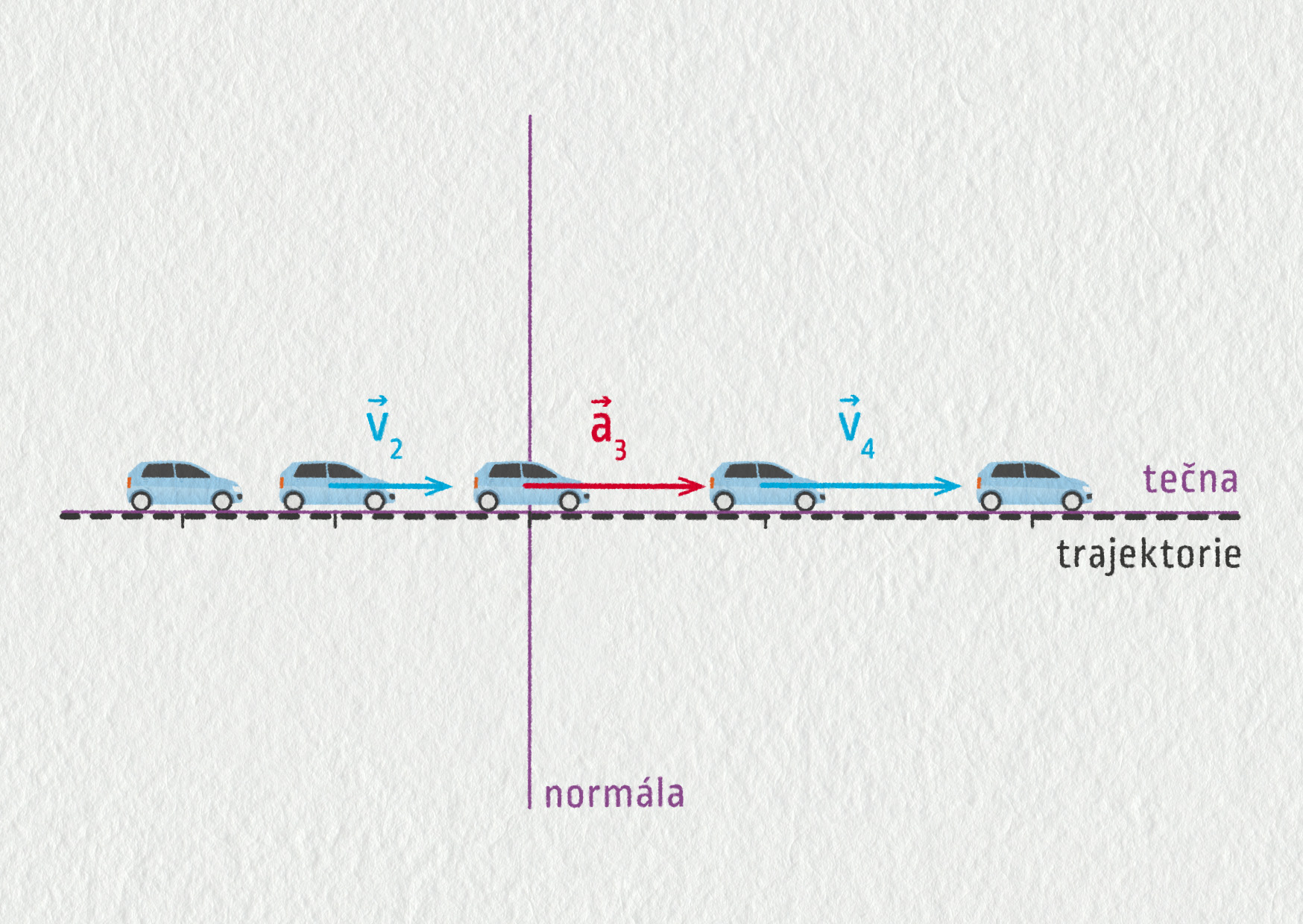
Zdroj
2) Předpokládejme, že auto projíždí zatáčkou po trajektorii tvaru kružnice rychlostí 45 km/h. Rychlost má stálou velikost, ale mění svůj směr. Jeho tečné zrychlení musí být nulové. Zrychlení tělesa je jen normálové (\(\Vec{a}=\Vec{a}_\mathrm{N}\)) a popisuje, jak se mění směr rychlosti, odpovídá zakřivení jeho trajektorie. Pro velikost normálového zrychlení lze odvodit obecný vztah \(a_\mathrm{N}=v^2/R\), kde \(R\) je poloměr kružnice v daném bodě trajektorie. Pohybu po kružnici se budeme věnovat podrobněji v následující kapitole.
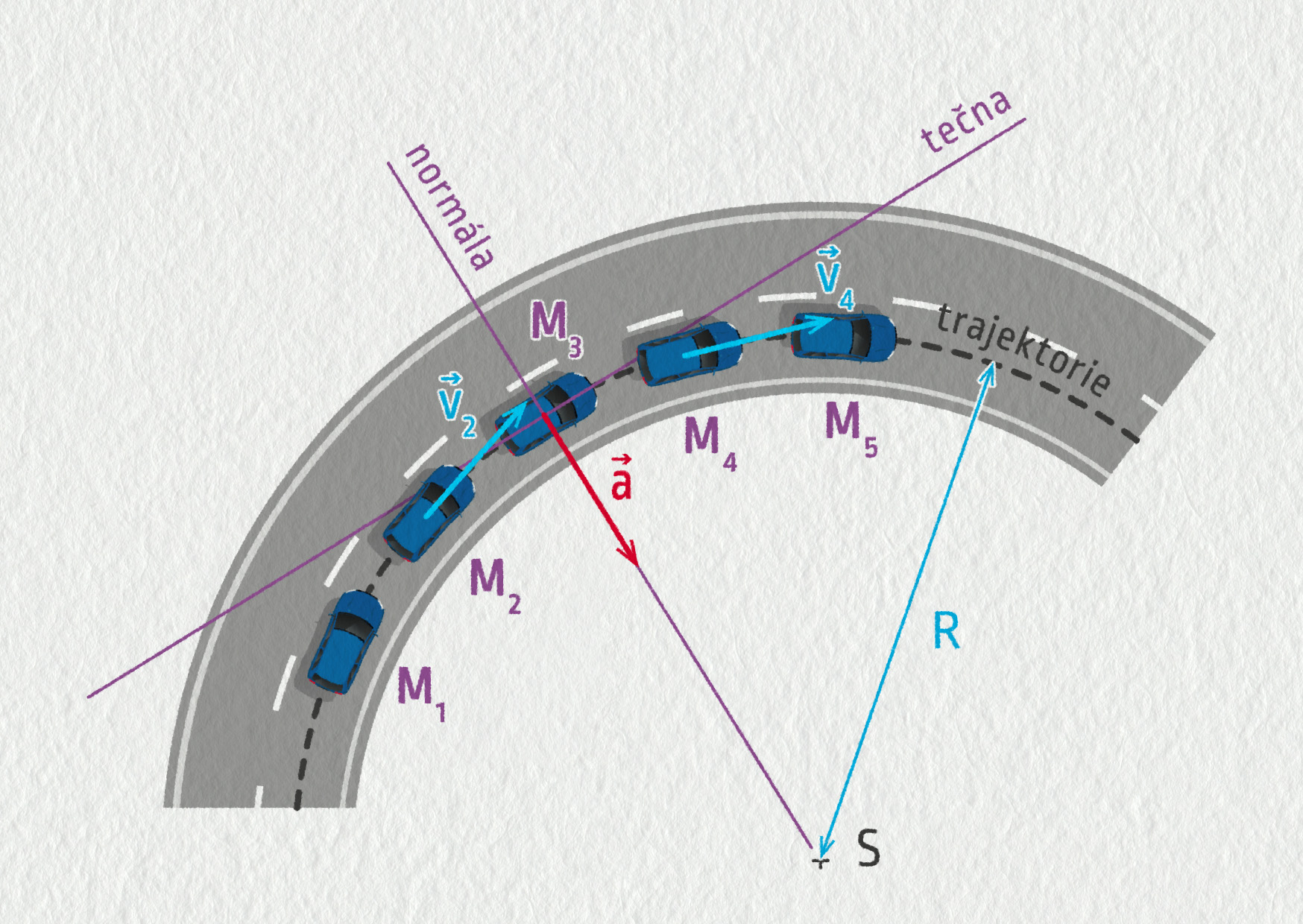
Zdroj
3) Auto při průjezdu zatáčkou zrychluje. Mění se směr i velikost jeho rychlosti. Obě zrychlení, tečné i normálové, jsou nenulová \(\Vec{a}=\Vec{a}_\mathrm{T}+\Vec{a}_\mathrm{N}\).
Zdroj
Rozdělení pohybů podle zrychlení shrnuje následující tabulka:
| pohyb | přímočarý | křivočarý |
|---|---|---|
| rovnoměrný | \(a_\mathrm{T}=0\), \(a_\mathrm{N}=0\) | \(a_\mathrm{T}=0\), \(a_\mathrm{N}\ne0\) |
| nerovnoměrný | \(a_\mathrm{T}\ne0\), \(a_\mathrm{N}=0\) | \(a_\mathrm{T}\ne0\), \(a_\mathrm{N}\ne0\) |
Na následujícím obrázku vidíme tři různé situace, ve kterých je zakreslena trajektorie tělesa a vektory rychlosti a zrychlení. Rozhodněte, zda dané zakreslení odpovídá reálné situaci, a proč ano, či proč ne.

Zdroj
- Tato situace je možná, rozložíme-li si zrychlení do směru tečného a normálového, vidíme, že normálové zrychlení směřuje dovnitř zakřivení a tečné zrychlení ve směru rychlosti. Těleso zatáčí a zrychluje.
- Tato situace možná není, protože normálové zrychlení směřuje vně zakřivení.
- Tato situace je možná. Tentokrát těleso zatáčí a nemění velikost rychlosti, protože tečné zrychlení je nulové.
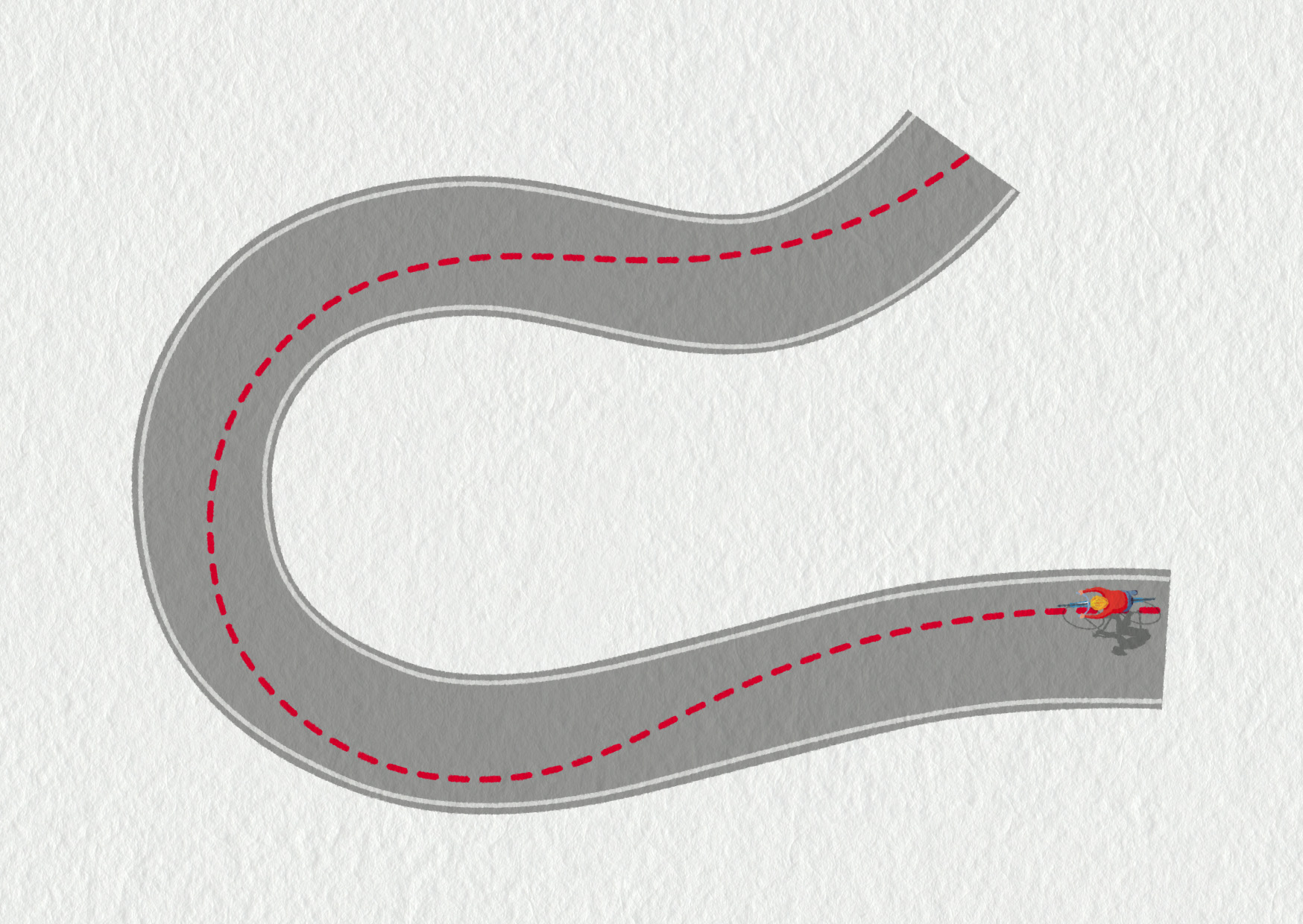
Zakreslete optimální trajektorii závodního cyklisty tak, aby mohl projet serpentinou co nejrychleji.

Zdroj
V běžném provozu takový průjezd zatáčkou ale nezkoušejte.
Cyklista si do zatáčky musí hodně „najet“, čímž zvětší poloměr své trajektorie, což při maximálním možném zrychlení \(a_N=v^2/R\) mu dovoluje jet vysokou rychlostí.
Zdroj
Jakou maximální rychlostí v m/s může motorkář projíždět zatáčku o poloměru 24 m, pokud jeho zrychlení nesmí překročit 6 m/s2? Odpověď zapište v m/s.

