Platí zákon setrvačnosti ve všech vztažných soustavách?
Představte si, že jedete v autobuse a řidič náhle začne brzdit. Co se stane, když nedržíte svůj kufr na kolečkách? Začne se pohybovat směrem k řidiči. Proč? Podívejme se na tuto situaci z pohledu dvou vztažných soustav.

Zdroj
- Z pohledu soustavy spojené se Zemí (maminka s kočárkem) je vše v pořádku. Kufr podle zákona setrvačnosti pokračuje v rovnoměrném přímočarém pohybu.
- Z pohledu soustavy spojené s autobusem (vy jako cestující a pozorovatel) byl kufr v klidu a najednou se dává do pohybu. V autobuse ani mimo něj ale nenajdete žádné těleso, které by na něj působilo směrem dopředu. To je porušení zákona setrvačnosti. Jak je to možné?
Pohybové zákony totiž neplatí ve všech soustavách. Newton uvažoval asi takto: Všechna tělesa, celý Vesmír, se nachází v jakési základní vztažné soustavě, nazval ji soustava spojená se stálicemi (tedy nehybnými hvězdami). V této soustavě formuloval svoje zákony. Tuto soustavu a soustavy, které jsou vůči ní buď v klidu, nebo v rovnoměrném přímočarém pohybu, nazýváme inerciální vztažné soustavy, (z latinského inertia – setrvání). Všechny soustavy, které se pohybují se zrychlením vůči inerciálním, se nazývají neinerciální. Pohybové zákony v nich neplatí. A to je právě příklad brzdícího autobusu.
Pozorovatel v neinerciální soustavě má pocit, že na tělesa působí ještě další síla, které říkáme setrvačná. Tato síla nevzniká působením mezi tělesy, ale tím, že situaci sledujeme z neinerciální vztažné soustavy. Proto se setrvačným silám říká také fiktivní neboli zdánlivé síly.
Setrvačnou sílu značíme \(\Vec{F}^*\) a můžeme ji určit, známe-li zrychlení neinerciální soustavy \(\Vec{a}^*\) vůči soustavám inerciálním a hmotnost pozorovaného tělesa m. Setrvačná síla má vždy opačný směr než zrychlení soustavy, platí \(\Vec{F}^*=-m\Vec{a}^*\).
Čili pokud chceme používat Newtonovy zákony i v neinerciálních soustavách, musíme mezi síly \(\sum_i\Vec{F}_i\) zahrnout i setrvačnou sílu \(\Vec{F}^*\).

Zdroj
Prakticky vzato můžeme bez problémů použít Newtonovu představu „stálic“ a soustavu spojenou s naší Galaxií považovat za inerciální. Podobně soustava spojená se Sluncem (heliocentrická vztažná soustava) se s obrovskou přesností chová jako inerciální, protože zrychlení, s jakým obíhá kolem středu Galaxie, je nepatrné. Při popisu jevů na povrchu Země pak používáme vztažnou soustavu spojenou s povrchem Země, říkáme jí laboratorní vztažná soustava. Ta, přísně vzato, není inerciální, neboť Země se otáčí kolem své osy. V některých specifických situacích se rotace Země může projevit (podrobnosti najdete pod heslem Coriolisova síla), ale ve většině případů můžeme i laboratorní soustavu považovat za inerciální.
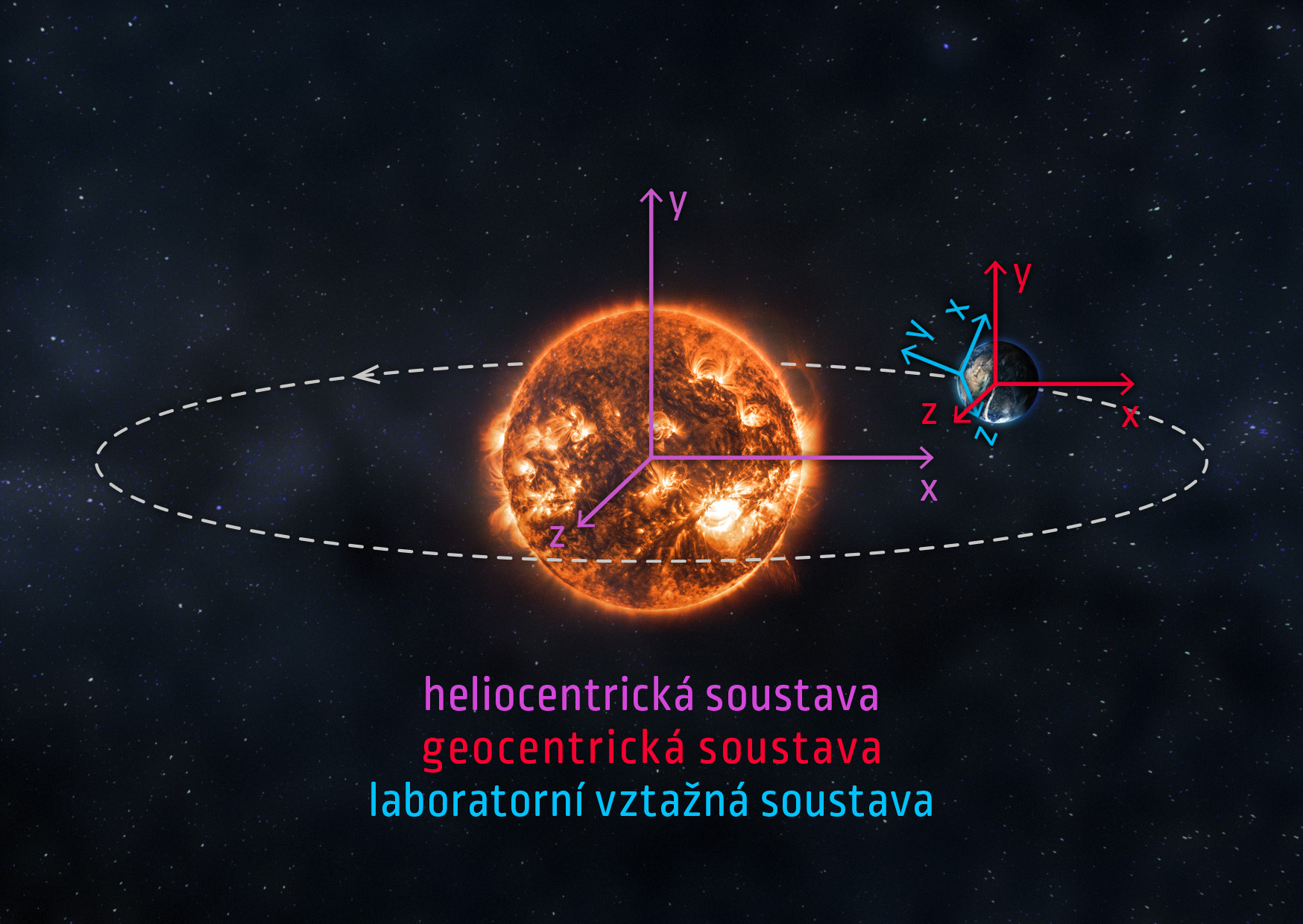
Zdroj
Mechanický model vesmíru
Vytvoření pohybových zákonů mělo značný vliv i na naše chápání časového vývoje vesmíru. Podle Newtona je určením počátečního stavu všech těles zcela přesně určena také jejich budoucnost. Tělesa se pouze řídí fyzikálními zákony, vesmír funguje jako dokonalý hodinový stroj. Je nutné podotknout, že sám Newton nebyl materialista, ale hluboce věřící člověk, a roli tvůrce zákonů a počátečního stavu vesmíru svěřil Bohu. Tato předurčenost se navíc týká jen materiálního světa. Důsledkem tohoto pohledu na svět tedy nutně nemusí být zánik svobodné vůle člověka, ale minimálně dokonalá předurčenost materiálního, fyzice dostupného světa.
V historii fyziky ovšem není o nečekané zvraty nouze. Počátkem 20. století se zrodila kvantová mechanika, která popisuje chování částic na mikroskopické úrovni, a přináší do fyziky prvek náhody. Například takový rozpad nestabilního jádra uranu je náhodný jev. Neexistuje možnost předpovědět, kdy k takovému jednomu rozpadu dojde. Dalším zajímavým zvratem byla ve stejné době rodící se teorie chaosu. Ta stručně řečeno dokázala, že i systém, který se řídí jednoduchými pohybovými zákony, se může za určitých podmínek chovat zcela nepředvídatelně – chaoticky. Je to proto, že libovolně malá odchylka v zadání počátečního stavu může způsobit zcela odlišný časový vývoj. Říká se tomu „efekt motýlích křídel” – mávnutí křídel motýla může ovlivnit vývoj počasí na celém kontinentu.

